极端量子性的正交基

由柏拉图重新发布

关注： 0

马尔辛·鲁津斯基^1,2, 亚当·伯查特³及卡罗尔·伊茨科夫斯基（KarolŻyczkowski）^1,4

¹雅盖隆大学物理，天文学和应用计算机科学学院，ul。 Polandojasiewicza 11，30-348克拉科夫，波兰
²雅盖隆大学精确与自然科学博士学院，ul。 Łojasiewicza 11, 30-348 克拉科夫, 波兰
³QuSoft、CWI 和阿姆斯特丹大学，Science Park 123, 1098 XG 阿姆斯特丹，荷兰
⁴波兰科学院理论物理中心，Al。 Lotników32/46，02-668华沙，波兰

觉得本文有趣或想讨论？在SciRate上发表评论或发表评论.

抽象

自旋反相干态作为最“量子”的态最近受到了广泛关注。一些相干和反相干自旋态被称为最佳量子旋转传感器。在这项工作中，我们引入了自旋态正交基的量子性度量，该度量由各个向量的平均反相干性和 Wehrl 熵决定。通过这种方式，我们确定了最相干和最量子态，从而实现了极端量子性的正交测量。它们的对称性可以使用马约拉纳恒星表示法来揭示，该表示法通过球体上的点提供了纯态的直观几何表示。获得的结果导致在由 $2j$ 量子位组成的多部分系统的 $1^{2j}$ 维空间的 $2j+2$ 维对称子空间中产生最大（最小）纠缠基。发现的一些碱基是等相干的，因为它们由具有相同程度的自旋相干性的所有状态组成。

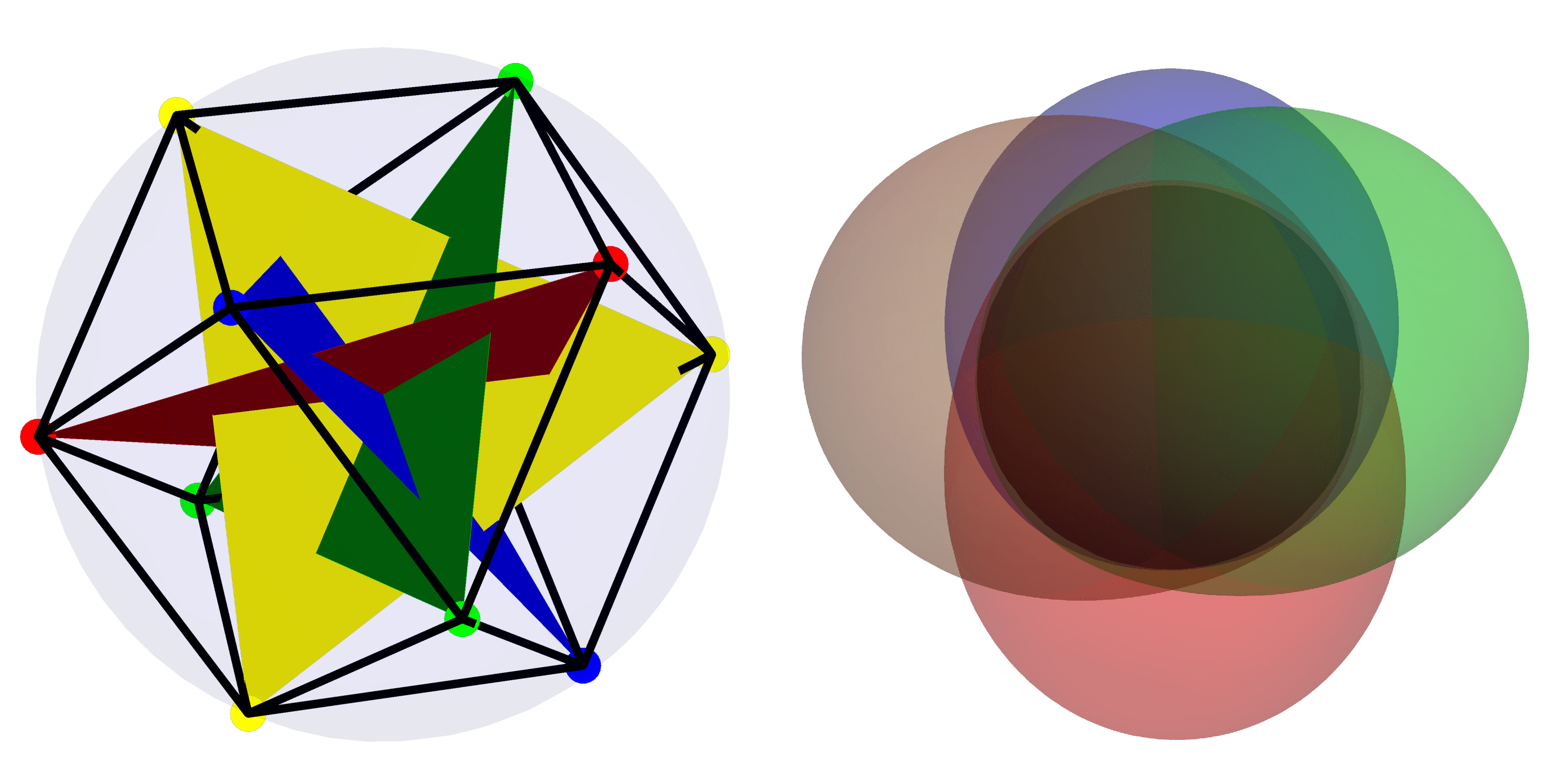
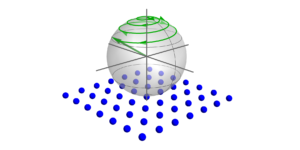
特色图片：在左图中，$mathcal{H}_4$ 中最“量子”的基础是使用恒星表示来描述的。右侧显示了 $mathcal{H}_4$ 内最一致（“经典”）基础上的状态的 Husimi 函数。

►BibTeX数据

@article{Rudzinski2024orthonormalbasesof, doi = {10.22331/q-2024-01-25-1234}, url = {https://doi.org/10.22331/q-2024-01-25-1234}, title = {Orthonormal bases of extreme quantumness}, author = {Rudzi{‘{n}}ski, Marcin and Burchardt, Adam and {.{Z}}yczkowski, Karol}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {8}, pages = {1234}, month = jan, year = {2024} }

►参考

[1] T. Frankel，《物理几何：简介》，第 3 版，剑桥大学出版社（2011 年）。
https：/ / doi.org/ 10.1017 / CBO9781139061377

[2] D. Chruściński 和 A. Jamiołkowski，《经典和量子力学中的几何相》，Birkhäuser (2004)。
https://doi.org/10.1007/978-0-8176-8176-0

[3] DA Lee，几何相对论，美国数学会，普罗维登斯（2021 年）。
https：/ / doi.org/ 10.1090 / gsm / 201

[4] I. Bengtsson 和 K. Życzkowski，《量子态几何：量子纠缠简介》，第二版，剑桥大学出版社（2 年）。
https：/ / doi.org/10.1017/ 9781139207010

[5] M. Lewin，非线性多体量子系统的几何方法，J. 功能分析 260, 12, (2011)。
https：///doi.org/10.1016/j.jfa.2010.11.017

[6] E. Cohen、H. Larocque、F. Bouchard 等人，从 Aharonov-Bohm 到 Pancharatnam-Berry 及以后的几何相，Nat。物理博士。 1, 437–449 (2019)。
https://doi.org/10.1038/s42254-019-0071-1

[7] E. 坎波磁变量中的东方原子 (Majorana Atomi orientati)，Nuovo Cimento 9, 43-50 (1932)。
https：/ / doi.org/ 10.1007 / BF02960953

[8] R. Barnett、A. Turner 和 E. Demler，旋量原子的新相分类，物理学。莱特牧师。 97、180412（2006）。
https：/ / doi.org/ 10.1103 / PhysRevLett.97.180412

[9] R. Barnett、A. Turner 和 E. Demler，$S=3$ 玻色-爱因斯坦凝聚中的涡流分类，物理学。修订版 A 76, 013605 (2007)。
https：/ / doi.org/ 10.1103 / PhysRevA.76.013605

[10] H. Mäkelä 和 K.-A. Suominen，自旋系统的惰性状态，物理学。莱特牧师。 99、190408（2007）。
https：/ / doi.org/ 10.1103 / PhysRevLett.99.190408

[11] E. Serrano-Ensástiga 和 F. Mireles，旋量玻色-爱因斯坦凝聚态的相表征：马约拉纳恒星表示方法，物理学。莱特。 A 492, 129188 (2023)。
https：///doi.org/10.1016/j.physleta.2023.129188

[12] P. Mathonet 等人，$N$-量子位对称态的纠缠等价，物理学。修订版 A 81, 052315 (2010)。
https：/ / doi.org/ 10.1103 / PhysRevA.81.052315

[13] J. Martin、O. Giraud、PA Braun、D. Braun 和 T. Bastin，具有高几何纠缠的多量子位对称态，Phys。修订版 A 81, 062347 (2010)。
https：/ / doi.org/ 10.1103 / PhysRevA.81.062347

[14] M. Aulbach、DJH Markham 和 M. Murao，几何测量方面的最大纠缠对称态，New J. Phys。 12、073025（2010）。
https://doi.org/10.1088/1367-2630/12/7/073025

[15] DJH Markham，排列对称态中的纠缠和对称性，物理学。修订版 A 83, 042332 (2011)。
https：/ / doi.org/ 10.1103 / PhysRevA.83.042332

[16] P. Ribeiro 和 R. Mosseri，$n$ 量子位对称扇区中的纠缠，物理学。莱特牧师。 106, 180502 (2011)。
https：/ / doi.org/ 10.1103 / PhysRevLett.106.180502

[17] M.Aulbach，对称态纠缠分类，Int。 J.量子信息。 10、1230004（2012）。
https：/ / doi.org/ 10.1142 / S0219749912300045

[18] W. Ganczarek、M. Kuś 和 K. Życzkowski，量子纠缠的重心测量，物理学。修订版 A 85, 032314 (2012)。
https：/ / doi.org/ 10.1103 / PhysRevA.85.032314

[19] A. Mandilara、T. Coudreau、A. Keller 和 P. Milman，通过自旋相干态对纯对称态进行纠缠分类，物理学。修订版 A 90, 050302(R) (2014)。
https：/ / doi.org/ 10.1103 / PhysRevA.90.050302

[20] P. Hyllus 等人，费希尔信息和多粒子纠缠，物理学。修订版 A 85, 022321 (2012)。
https：/ / doi.org/ 10.1103 / PhysRevA.85.022321

[21] JH Hannay，马约拉纳表示中旋转的贝里相，J. Phys。答：数学。第 31 代，L53 (1998)。
https://doi.org/10.1088/0305-4470/31/2/002

[22] P. Bruno，马约拉纳恒星表示中的量子几何相位：映射到多体阿哈罗诺夫-博姆相位，物理学。莱特牧师。 108, 240402 (2012)。
https：/ / doi.org/ 10.1103 / PhysRevLett.108.240402

[23] HD Liu 和 LB Fu，马约拉纳恒星表示中的贝里相和量子纠缠，物理学。修订版 A 94, 022123 (2016)。
https：/ / doi.org/ 10.1103 / PhysRevA.94.022123

[24] P. Ribeiro、J. Vidal 和 R. Mosseri，Lipkin-Meshkov-Glick 模型的热力学极限，物理学。莱特牧师。 99, 050402 (2007)。
https：/ / doi.org/ 10.1103 / PhysRevLett.99.050402

[25] P. Ribeiro、J. Vidal 和 R. Mosseri，热力学极限和有限尺寸修正中 Lipkin-Meshkov-Glick 模型的精确谱，Phys。修订版 E 78, 021106 (2008)。
https：/ / doi.org/ 10.1103 / PhysRevE.78.021106

[26] J. Zimba，通过马约拉纳表示的“反相干”自旋态，电子。 J.理论。物理。 3, 143 (2006)。
https:// / api.semanticscholar.org/ CorpusID:13938120

[27] D. Baguette、T. Bastin 和 J. Martin，具有最大混合单量子位约简的多量子位对称态，Phys。修订版 A 90, 032314 (2014)。
https：/ / doi.org/ 10.1103 / PhysRevA.90.032314

[28] O. Giraud、D. Braun、D. Baguette、T. Bastin 和 J. Martin，自旋态的张量表示，物理学。莱特牧师。 114, 080401 (2015)。
https：/ / doi.org/ 10.1103 / PhysRevLett.114.080401

[29] D. Baguette、F. Damanet、O. Giraud 和 J. Martin，具有点群对称性的自旋态的反相干性，物理学。修订版 A 92, 052333 (2015)。
https：/ / doi.org/ 10.1103 / PhysRevA.92.052333

[30] HD Liu，LB Fu，X. Wang，马约拉纳表示的一致状态方法，Commun。理论。物理。 67、611（2017）。
https://doi.org/10.1088/0253-6102/67/6/611

[31] D. Baguette 和 J. Martin，纯自旋态的反相干测量，物理学。修订版 A 96, 032304 (2017)。
https：/ / doi.org/ 10.1103 / PhysRevA.96.032304

[32] P. Kolenderski 和 R. Demkowicz-Dobrzański，保持参考系对齐和柏拉图固体的最佳状态，Phys。修订版 A 78, 052333 (2008)。
https：/ / doi.org/ 10.1103 / PhysRevA.78.052333

[33] C. Chryssomalakos 和 H. Hernández-Coronado，最佳量子旋转传感器，物理学。修订版 A 95, 052125 (2017)。
https：/ / doi.org/ 10.1103 / PhysRevA.95.052125

[34] AZ Goldberg 和 DFV James，使用反相干态的量子限制欧拉角测量，物理学。修订版 A 98, 032113 (2018)。
https：/ / doi.org/ 10.1103 / PhysRevA.98.032113

[35] J. Martin、S. Weigert 和 O. Giraud，通过相干和反相干态对未知轴旋转的最佳检测，Quantum 4, 285 (2020)。
https://doi.org/10.22331/q-2020-06-22-285

[36] J. Crann、DW Kribs 和 R. Pereira，球形设计和反相干自旋态，J. Phys。答：数学。理论。 43、255307（2010）。
https://doi.org/10.1088/1751-8113/43/25/255307

[37] E. Bannai 和 M. Tagami，关于反相干自旋态的注释，J. Phys。答：数学。理论。 44, 342002 (2011)。
https://doi.org/10.1088/1751-8113/44/34/342002

[38] M. Wang 和 Y. Zhu，反相干自旋 2 态和球形设计，J. Phys。答：数学。理论。 55, 425304 (2022)。
https://doi.org/10.1088/1751-8121/ac971d

[39] AZ Goldberg、AB Klimov、M.Grassl、G. Leuchs 和 LL Sánchez-Soto，极端量子态，AVS 量子科学。 2、044701（2020）。
https：/ / doi.org/10.1116/ 5.0025819

[40] AZ Goldberg、M. Grassl、G. Leuchs 和 LL Sánchez-Soto，超越纠缠的量子性：对称态的情况，物理学。修订版 A 105, 022433 (2022)。
https：/ / doi.org/ 10.1103 / PhysRevA.105.022433

[41] O. Giraud、P. Braun 和 D. Braun，量化量子性和寻找量子女王，New J. Phys。 12、063005（2010）。
https://doi.org/10.1088/1367-2630/12/6/063005

[42] R. Delbourgo，轮换组和联合组的最小不确定性状态，J. Phys。 A 10，L233 (1977)。
https://doi.org/10.1088/0305-4470/10/11/012

[43] A. Wehrl，论经典熵和量子力学熵之间的关系，Rep. Math。物理。 16, 353 (1979)。
https://doi.org/10.1016/0034-4877(79)90070-3

[44] EH Lieb，Wehrl 熵猜想的证明，Commun。数学。物理。 62, 35 (1978)。
https：/ / doi.org/ 10.1007 / BF01940328

[45] CT Lee，韦尔自旋态熵和利布猜想，J. Phys。 A 21, 3749 (1988)。
https://doi.org/10.1088/0305-4470/21/19/013

[46] EH Lieb 和 JP Solovej，布洛赫相干自旋态熵猜想及其推广的证明，数学学报。 212, 379 (2014)。
https://doi.org/10.1007/s11511-014-0113-6

[47] F. Bouchard 等人，极值马约拉纳星座极限量子计量，Optica 4, 1429-1432 (2017)。
https：///doi.org/10.1364/OPTICA.4.001429

[48] A. Wehrl，熵的一般性质，Rev. Mod。物理。 50, 221 (1978)。
https：/ / doi.org/ 10.1103 / RevModPhys.50.221

[49] A. Wehrl，熵的许多方面，Rep. Math。物理。 30, 119 (1991)。
https://doi.org/10.1016/0034-4877(91)90045-O

[50] S. Gnutzmann 和 K. Życzkowski，Renyi-Wehrl 熵作为相空间局部化的度量，J. Phys。 A 34, 10123 (2001)。
https://doi.org/10.1088/0305-4470/34/47/317

[51] K. Życzkowski，本征态本地化和平均 Wehrl 熵，Physica E 9, 583 (2001)。
https://doi.org/10.1016/S1386-9477(00)00266-6

[52] LL Sánchez-Soto、AB Klimov、P. de la Hoz 和 G. Leuchs，量子偏振态与经典偏振态：当多极计数时，J. Phys。 B 46 104011 (2013)。
https://doi.org/10.1088/0953-4075/46/10/104011

[53] A. Tavakoli 和 N. Gisin，柏拉图固体和量子力学的基本测试，Quantum 4, 293 (2020)。
https://doi.org/10.22331/q-2020-07-09-293

[54] H.Ch. Nguyen、S. Designolle、M. Barakat 和 O. Gühne，量子力学测量之间的对称性，预印本 arXiv：2003.12553 (2022)。
https://doi.org/10.48550/arXiv.2003.12553
的arXiv：2003.12553

[55] JI Latorre 和 G. Sierra，柏拉图式纠缠，量子信息。计算。 21, 1081 (2021)。
https：/ / doi.org/ 10.26421 / QIC21.13-14-1

[56] K. Bolonek-Lasoń 和 P. Kosiński，群、柏拉图固体和贝尔不等式，Quantum 5, 593 (2021)。
https://doi.org/10.22331/q-2021-11-29-593

[57] KF Pál 和 T. Vértesi，群，所有维度的柏拉图贝尔不等式，Quantum 6, 756 (2022)。
https://doi.org/10.22331/q-2022-07-07-756

[58] RH Dicke，自发辐射过程的相干性，物理学。修订版 93, 99 (1954)。
https：/ / doi.org/ 10.1103 / PhysRev.93.99

[59] V. Karimipour 和 L. Memarzadeh，任意维度的等纠缠碱基 Phys。修订版 A 73, 012329 (2006)。
https：/ / doi.org/ 10.1103 / PhysRevA.73.012329

[60] G. Rajchel、A. Gąsiorowski 和 K. Życzkowski，鲁棒 Hadamard 矩阵、Birkhoff 多面体中的单随机射线以及复合空间中的等纠缠基。比较。科学。 12, 473 (2018)。
https：/ / doi.org/ 10.1007 / s11786-018-0384-y

[61] J. Czartowski、D. Goyeneche、M. Grassl 和 K. Życzkowski，等纠缠互无偏基、对称量子测量和混合态设计，Phys。莱特牧师。 124, 090503 (2020)。
https：/ / doi.org/ 10.1103 / PhysRevLett.124.090503

[62] F. Del Santo、J. Czartowski、K. Życzkowski 和 N. Gisin，Iso 纠缠碱基和联合测量，预印本 arXiv：2307.06998 (2023)。
https://doi.org/10.48550/arXiv.2307.06998
的arXiv：2307.06998

[63] R. Penrose，论没有概率的贝尔非局域性：一些奇怪的几何学，量子反射（2000）。

[64] J. Zimba 和 R. Penrose，论无概率的贝尔非局域性：更好奇的几何学，Stud。历史。菲尔.科学。 24, 697 (1993)。
https://doi.org/10.1016/0039-3681(93)90061-N

[65] JE Massad 和 PK Aravind，重新审视彭罗斯十二面体，Am。物理学杂志 67, 631 (1999)。
https：/ / doi.org/10.1119/ 1.19336

[66] K. Husimi，密度矩阵的一些形式属性，Proc。物理。数学。苏克。 22, 264 (1940)。
https：///doi.org/10.11429/ppmsj1919.22.4_264

[67] W. Słomczyński 和 K. Życzkowski，球体上量子图的平均动态熵在半经典极限内发散，Phys。莱特牧师。 80、1880（1998）。
https：/ / doi.org/ 10.1103 / PhysRevLett.80.1880

[68] M. Piotrak、M. Kopciuch、AD Fard、M. Smolis、S. Pustelny、K. Korzekwa，完美量子量角器，预印本 arXiv：2310.13045 (2023)。
https://doi.org/10.48550/arXiv.2310.13045
的arXiv：2310.13045

[69] NCN Maestro 7 2015/18/A/ST2/00274 网站 https://chaos.if.uj.edu.pl/karol/Maestro7/files/data3/Numerical_Results.dat。
https://chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

[70] D. Weingarten，无限秩极限下群积分的渐近行为，J. Math。物理。 19, 999 (1978)。
https：/ / doi.org/10.1063/ 1.523807

[71] B. Collins 和 P. Śniady，关于酉、正交和辛群的 Haar 测度的积分，Commun。数学。物理。 264, 773 (2006)。
https://doi.org/10.1007/s00220-006-1554-3

[72] G. Rajchel，量子映射和设计，博士论文，预印本 arXiv:2204.13008 (2022)。
https://doi.org/10.48550/arXiv.2204.13008
的arXiv：2204.13008

[73] D. Martin 和 EP Wigner，群论及其在原子光谱量子力学中的应用，Academic Press Inc. NY (1959)。
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

被引用

[1] Michał Piotrak、Marek Kopciuch、Arash Dezhang Fard、Magdalena Smolis、Szymon Pustelny 和 Kamil Korzekwa，“完美的量子量角器”，的arXiv：2310.13045, (2023).

[2] Aaron Z. Goldberg，“对称态粒子子集的相关性：当其余部分被忽略时，光子在一束光中正在做什么”，的arXiv：2401.05484, (2024).

以上引用来自 SAO / NASA广告（最近成功更新为2024-01-25 11:53:23）。该列表可能不完整，因为并非所有发布者都提供合适且完整的引用数据。

无法获取 Crossref引用的数据在上一次尝试2024-01-25 11:53:22期间：无法从Crossref获取10.22331 / q-2024-01-25-1234的引用数据。如果DOI是最近注册的，这是正常的。

该论文发表在《量子》杂志上国际知识共享署名署名4.0（CC BY 4.0）执照。版权归原始版权持有者所有，例如作者或其所在机构。

SEO 支持的内容和 PR 分发。今天得到放大。
PlatoData.Network 垂直生成人工智能。赋予自己力量。访问这里。
柏拉图爱流。 Web3 智能。知识放大。访问这里。
柏拉图ESG。碳，清洁科技, 能源，环境，太阳能，废物管理。访问这里。
柏拉图健康。生物技术和临床试验情报。访问这里。
Sumber: https://quantum-journal.org/papers/q-2024-01-25-1234/

时间戳记： 2024 年 1 月 25 日

时间戳记： 2023 年 10 月 3 日

由柏拉图重新发布

抽象

热门摘要

►BibTeX数据

►参考

被引用

更多来自量子杂志

通过有限大小分析改进 DIQKD 协议

遥控纠缠生成

具有随机测量的快速量子电路切割

基于测量的连续变量集群状态中猫和网格状态的生成和保存

通过绝热螺旋在海森堡模型中进行状态准备

MQT Bench：量子计算的基准测试软件和设计自动化工具

解析性约束限制了光谱形状因子的衰减

二维空间维度中费米子到量子比特映射的变分解

规范理论和玻色子系统的可证明准确的模拟

连续时间随机过程的量子编码和分析及其金融应用

关于我们

垂直搜索和Ai

应用平台

保持联系

账号管理

抽象

被引用

更多来自 量子杂志