1巴斯克大学理论物理学 UPV/EHU,ES-48080 毕尔巴鄂,西班牙
2EHU Quantum Center, University of the Basque Country UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscay, 西班牙
3Donostia 国际物理中心 (DIPC),ES-20080 西班牙圣塞瓦斯蒂安
4IKERBASQUE,巴斯克科学基金会,ES-48011 毕尔巴鄂,西班牙
5固体物理和光学研究所,维格纳物理研究中心,HU-1525 布达佩斯,匈牙利
6阿尔弗雷德·雷尼数学研究所,Reáltanoda u。 13-15., HU-1053 布达佩斯, 匈牙利
7布达佩斯技术经济大学数学研究所分析与运筹学系,Müegyetem rkp。 3., HU-1111 布达佩斯, 匈牙利
觉得本文有趣或想讨论? 在SciRate上发表评论或发表评论.
抽象
我们定义了量子 Wasserstein 距离,以便在二分可分离态而不是一般的二分量子态上进行耦合优化,并检查其性质。 令人惊讶的是,我们发现自距离与量子费希尔信息有关。 我们提出了与最佳二分可分离状态相对应的传输图。 我们讨论引入的量子 Wasserstein 距离如何与检测量子纠缠的标准联系起来。 我们定义了类方差量,可以通过用最大化代替量子态的最小化来从量子 Wasserstein 距离获得。 我们将结果扩展到一系列广义量子费希尔信息量。
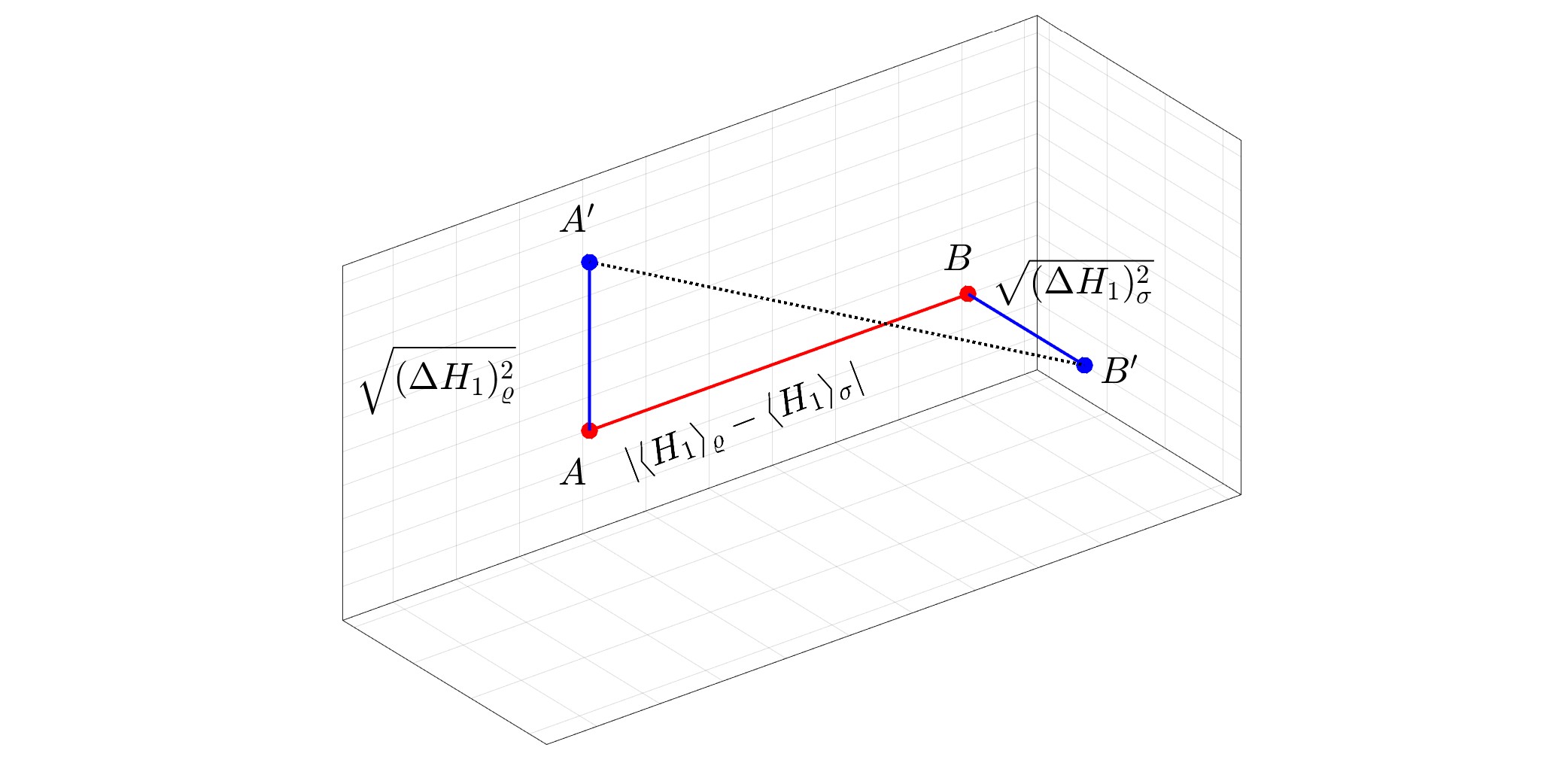
特色图片:$N=1 时纯态 $varrho$ 和混合态 $sigma$ 之间量子 Wasserstein 距离的几何表示。$ 量子 Wasserstein 距离等于 $1/sqrt2$ 乘以 $A'$ 之间通常的欧几里得距离和$B'.$
热门摘要
距离在数学、物理和工程学中起着核心作用。 概率和统计学的一个基本问题是提出两个概率分布之间距离的有用度量。 不幸的是,概率分布之间的许多距离概念,例如 p(x) 和 q(x),如果它们彼此不重叠,则它们是最大的,即,当另一个不为零时,一个始终为零。 这对于许多应用来说是不切实际的。 例如,回到沙子的类比,两堆不重叠的沙子似乎彼此距离相等,无论它们的距离是 10 公里还是 100 公里。 最优传输理论是一种构建概率分布之间距离的替代概念的方法,即所谓的 Wasserstein 距离。 即使分布彼此不重叠,它也可以是非最大的,它对基础指标(即传输成本)很敏感,本质上,它表达了我们将一个分布转移到另一个分布所需的努力,就好像它们是沙丘一样。
最近,量子 Wasserstein 距离被定义为推广经典 Wasserstein 距离。 它基于二分量子系统的量子态上成本函数的最小化。 它具有类似于上面提到的量子世界中的性质。 对于正交态,它可以是非极大值,例如,当我们需要将量子数据教授给算法时,这很有用。
正如我们所预料的,量子 Wasserstein 距离还具有与其经典对应物非常不同的属性。 例如,当我们测量量子态与其自身的距离时,它可以是非零的。 虽然这已经令人费解,但人们还发现,自距离与 Wigner-Yanase 偏斜信息有关,该信息由诺贝尔奖获得者 EP Wigner 于 1963 年提出,他对量子物理学和 MM Yanase 的基础做出了重要贡献。
在我们的论文中,我们从另一个方向看待这个神秘的发现。 我们将上述最小化限制为所谓的可分离状态。 这些是不包含纠缠的量子态。 我们发现自距离成为量子费希尔信息,这是量子计量学和量子估计理论的核心量,并出现在例如著名的克拉默-饶界中。 通过研究这种瓦瑟斯坦距离的性质,我们的工作为将量子瓦瑟斯坦距离理论与量子纠缠理论联系起来铺平了道路。
►BibTeX数据
►参考
[1] G.蒙日. “关于 déblais et des remblais 理论的回忆录”。 巴黎皇家科学院回忆录 (1781)。
[2] L·坎托洛维奇。 《论群众的转移》。 管理科学 5, 1–4 (1958)。 网址:http://www.jstor.org/stable/2626967。
http://www.jstor.org/stable/2626967
[3] 伊曼纽尔·布瓦萨尔、蒂博·勒古伊克和让-米歇尔·卢布。 “使用 Wasserstein 指标进行分布模板估计”。 伯努利 21, 740–759 (2015)。
https:///doi.org/10.3150/13-bej585
[4] 奥列格·布特科夫斯基。 “Wasserstein 度量中马尔可夫过程的亚几何收敛率”。 安. 应用。 很可能。 24, 526–552 (2014)。
https:///doi.org/10.1214/13-AAP922
[5] M.海勒,J.-C。 马丁利和 M. Scheutzow。 “渐近耦合和哈里斯定理的一般形式及其在随机延迟方程中的应用”。 很可能。 理论相关。 领域 149, 223–259 (2011)。
https://doi.org/10.1007/s00440-009-0250-6
[6] M. 海勒和 JC 马丁利。 “Wasserstein 距离中的谱间隙和二维随机纳维-斯托克斯方程”。 安. 很可能。 2,36-2050(2091)。
https:/ / doi.org/ 10.1214/ 08-AOP392
[7] A. Figalli、F. Maggi 和 A. Pratelli。 “定量等周不平等的大众交通方法”。 发明。 数学。 182、167-211。 (2010)。
https:/ / doi.org/ 10.1007 / s00222-010-0261-z
[8] A. Figalli 和 F. Maggi。 “关于小质量状态下液滴和晶体的形状”。 拱。 配给。 机甲。 肛门。 201, 143–207 (2011)。
https:///doi.org/10.1007/s00205-010-0383-x
[9] J.洛特和C.维拉尼。 “通过最佳传输实现度量测量空间的里奇曲率”。 安. 数学。 169 (3), 903–991 (2009)。
https://doi.org/10.48550/arXiv.math/0412127
[10] 最大-K。 冯·雷内斯和卡尔-西奥多·斯特姆。 “传输不等式、梯度估计、熵和里奇曲率”。 通讯。 纯应用。 数学。 58, 923–940 (2005)。
https:///doi.org/10.1002/cpa.20060
[11] 卡尔-西奥多·斯特姆。 “论度量空间的几何I”。 数学学报。 196, 65–131 (2006)。
https://doi.org/10.1007/s11511-006-0002-8
[12] 卡尔-西奥多·斯特姆。 “论度量测度空间的几何学II”。 数学学报。 196, 133–177 (2006)。
https://doi.org/10.1007/s11511-006-0003-7
[13] 贝诺伊特·克洛克纳。 “瓦瑟斯坦空间的几何研究:欧几里得空间”。 比萨高等师范学校年鉴 – 科学类,高等师范学校 2010 IX (2), 297–323 (2010)。
https:/ / doi.org/ 10.2422 / 2036-2145.2010.2.03
[14] György Pál Gehér、Tamás Titkos 和 Dániel Virosztek。 “关于 Wasserstein 空间的等距嵌入——离散情况”。 J.马斯。 肛门。 应用。 480, 123435 (2019)。
https://doi.org/10.1016/j.jmaa.2019.123435
[15] György Pál Gehér、T. Titkos、Dániel Virosztek。 “瓦瑟斯坦空间的等距研究——实线”。 跨。 阿米尔。 数学。 苏克。 373, 5855–5883 (2020)。
https:///doi.org/10.1090/tran/8113
[16] György Pál Gehér、Tamás Titkos 和 Dániel Virosztek。 “Wasserstein 空间的等距群:希尔伯特案例”。 J·隆德. 数学。 苏克。 106, 3865–3894 (2022)。
https://doi.org/10.1112/jlms.12676
[17] György Pál Gehér、Tamás Titkos 和 Dániel Virosztek。 “wasserstein 环面和球体的等距刚性”。 数学 69, 20–32 (2023)。
https://doi.org/10.1112/mtk.12174
[18] 盖尔盖利·基斯和塔马斯·蒂特科斯。 “wasserstein 空间的等距刚性:图度量案例”。 过程。 是。 数学。 苏克。 150, 4083–4097 (2022)。
https:/ / doi.org/ 10.1090/ proc/ 15977
[19] György Pál Gehér、Tamás Titkos 和 Dániel Virosztek。 “关于二次 Wasserstein 空间在实线上的奇异等距流”。 线性代数应用(2023)。
https:///doi.org/10.1016/j.laa.2023.02.016
[20] S. Kolouri、SR Park 和 GK Rohde。 “氡累积分布变换及其在图像分类中的应用”。 IEEE 传输。 图像处理。 25, 920–934 (2016)。
https:/ / doi.org/ 10.1109/ TIP.2015.2509419
[21] W. Wang、D. Slepc̆ev、S. Basu、JA Ozolek 和 GK Rohde。 “用于量化和可视化图像组变化的线性最佳传输框架”。 国际。 J. 计算机。 维斯。 101, 254–269 (2013)。
https:/ / doi.org/ 10.1007 / s11263-012-0566-z
[22] S. Kolouri、S. Park、M. Thorpe、D. Slepc̆ev、GK Rohde。 “最佳质量传输:信号处理和机器学习应用”。 IEEE 信号处理杂志 34, 43–59 (2017)。
https:///doi.org/10.1109/MSP.2017.2695801
[23] A. Gramfort、G. Peyré 和 M. Cuturi。 “神经影像数据的快速最佳传输平均”。 医学成像中的信息处理。 IPMI 2015。计算机科学讲义 9123, 261–272 (2015)。
https://doi.org/10.1007/978-3-319-19992-4_20
[24] Z. Su,W. Zeng,Y. Wang,ZL Lu 和 X. Gu。 “使用 Wasserstein 距离进行形状分类进行大脑形态测量分析”。 医学成像中的信息处理。 IPMI 2015。计算机科学讲义 24, 411–423 (2015)。
https://doi.org/10.1007/978-3-319-19992-4_32
[25] 马丁·阿约夫斯基、苏米特·钦塔拉和莱昂·博图。 “Wasserstein 生成对抗网络”。 Doina Precup 和 Yee Whye Teh,编辑,《第 34 届国际机器学习会议论文集》。 《机器学习研究论文集》第 70 卷,第 214-223 页。 PMLR(2017)。 arXiv:1701.07875。
的arXiv:1701.07875
[26] TA El Moselhy 和 YM Marzouk。 “具有最佳映射的贝叶斯推理”。 J. 计算机。 物理。 231, 7815–7850 (2012)。
https:///doi.org/10.1016/j.jcp.2012.07.022
[27] 加布里埃尔·佩雷和马可·库图里。 “计算最优传输:在数据科学中的应用”。 成立。 趋势机器学习。 11, 355–602 (2019)。
https:/ / doi.org/10.1561/ 2200000073
[28] 查理·弗罗格纳、张驰远、侯赛因·莫巴希、毛里西奥·阿拉亚和托马索·波吉奥。 “带着瓦瑟斯坦的损失学习”。 C. Cortes、N. Lawrence、D. Lee、M. Sugiyama 和 R. Garnett,编辑,《神经信息处理系统进展》。 第 28 卷。Curran Associates, Inc. (2015)。 arXiv:1506.05439。
的arXiv:1506.05439
[29] A. Ramdas、NG Trillos 和 M. Cuturi。 “关于 Wasserstein 双样本检验和非参数检验的相关系列”。 熵 19, 47. (2017)。
https:///doi.org/10.3390/e19020047
[30] S. Srivastava、C. Li 和 DB Dunson。 “通过 Wasserstein 空间中的重心进行可扩展贝叶斯”。 J.马赫. 学习。 资源。 19, 1–35 (2018)。 arXiv:1508.05880。
的arXiv:1508.05880
[31] 卡罗尔·兹科夫斯基和沃耶切赫·斯洛姆琴斯基。 “量子态之间的蒙日距离”。 J. Phys。 答:数学。 Gen. 31, 9095–9104 (1998)。
https://doi.org/10.1088/0305-4470/31/45/009
[32] 卡罗尔·兹科夫斯基和沃伊切赫·斯洛姆钦斯基。 “关于量子态球体和几何的蒙日度量”。 J. Phys。 答:数学。 创 34, 6689–6722 (2001)。
https://doi.org/10.1088/0305-4470/34/34/311
[33] Ingemar Bengtsson 和 Karol Życzkowski。 “量子态几何:量子纠缠简介”。 剑桥大学出版社。 (2006)。
https:/ / doi.org/ 10.1017 / CBO9780511535048
[34] P. Biane 和 D. Voiculescu。 “迹状态空间上 Wasserstein 度量的自由概率模拟”。 GAFA,吉姆。 功能。 肛门。 11, 1125–1138 (2001)。
https://doi.org/10.1007/s00039-001-8226-4
[35] 埃里克·A·卡伦和扬·马斯。 “非交换概率中 2-Wasserstein 度量的模拟,其中费米子福克-普朗克方程是熵的梯度流”。 交流。 数学。 物理。 331, 887–926 (2014)。
https://doi.org/10.1007/s00220-014-2124-8
[36] 埃里克·A·卡伦和扬·马斯。 “具有详细平衡的量子马尔可夫半群的梯度流和熵不等式”。 J.函数。 肛门。 273, 1810–1869 (2017)。
https:///doi.org/10.1016/j.jfa.2017.05.003
[37] 埃里克·A·卡伦和扬·马斯。 “耗散量子系统中的非交换微积分、最优传输和函数不等式”。 J. 统计。 物理。 178, 319–378 (2020)。
https:/ / doi.org/ 10.1007 / s10955-019-02434-w
[38] 尼兰贾纳·达塔和坎比斯·鲁泽。 “量子函数和运输成本不等式导致的量子态集中”。 J.马斯。 物理。 60, 012202 (2019)。
https:/ / doi.org/10.1063/ 1.5023210
[39] 尼兰贾纳·达塔和坎比斯·鲁泽。 “关联相对熵、最优传输和 Fisher 信息:量子 HWI 不等式”。 安. 亨利·庞加莱 21, 2115–2150 (2020)。
https://doi.org/10.1007/s00023-020-00891-8
[40] 弗朗索瓦·戈尔斯、克莱门特·穆奥和蒂埃里·保罗。 “论量子力学的平均场和经典极限”。 交流。 数学。 物理。 343, 165–205 (2016)。
https://doi.org/10.1007/s00220-015-2485-7
[41] 弗朗索瓦·戈尔斯和蒂埃里·保罗。 “平均场和半经典体系中的薛定谔方程”。 拱。 配给。 机甲。 肛门。 223, 57–94 (2017)。
https:///doi.org/10.1007/s00205-016-1031-x
[42] 弗朗索瓦·戈尔斯和蒂埃里·保罗。 “量子力学中的波包和二次蒙日-坎托罗维奇距离”。 完成 Rendus Math。 356, 177–197 (2018)。
https://doi.org/10.1016/j.crma.2017.12.007
[43] 弗朗索瓦·戈尔斯. “平均场和半经典体系中的量子 $N$ 体问题”。 菲尔. 跨。 R.苏克。 A 376,20170229(2018)。
https:/ / doi.org/ 10.1098 / rsta.2017.0229
[44] E.卡廖蒂、F.戈尔斯和T.保罗。 “量子最优传输更便宜”。 J. 统计。 物理。 181, 149–162 (2020)。
https://doi.org/10.1007/s10955-020-02571-7
[45] 埃马努埃莱·卡廖蒂、弗朗索瓦·戈尔斯和蒂埃里·保罗。 “迈向量子密度的最佳传输”。 arXiv:2101.03256 (2021)。
https://doi.org/10.48550/arXiv.2101.03256
的arXiv:2101.03256
[46] 贾科莫·德·帕尔马和达里奥·特雷维桑。 “量子通道的量子最优传输”。 安. 亨利·庞加莱 22, 3199–3234 (2021)。
https://doi.org/10.1007/s00023-021-01042-3
[47] 贾科莫·德·帕尔马、米拉德·马维安、达里奥·特雷维桑和塞斯·劳埃德。 “1 阶量子 Wasserstein 距离”。 IEEE 传输。 信息。 理论 67, 6627–6643 (2021)。
https:///doi.org/10.1109/TIT.2021.3076442
[48] 什穆尔·弗里德兰、米哈乌·埃克斯坦、萨姆·科尔和卡罗尔·兹科夫斯基。 “量子蒙日-康托罗维奇问题和密度矩阵之间的传输距离”。 物理。 莱特牧师。 129, 110402 (2022)。
https:/ / doi.org/ 10.1103 / PhysRevLett.129.110402
[49] 萨姆·科尔、米哈乌·埃克斯坦、什穆尔·弗里德兰和卡罗尔·兹科夫斯基。 “量子最优传输”。 arXiv:2105.06922 (2021)。
https://doi.org/10.48550/arXiv.2105.06922
的arXiv:2105.06922
[50] R. Bistroń、M. Eckstein 和 K. Życzkowski。 “量子 2-Wasserstein 距离的单调性”。 J. Phys。 答:数学。 理论。 56, 095301 (2023)。
https://doi.org/10.1088/1751-8121/acb9c8
[51] György Pál Gehér、József Pitrik、Tamás Titkos 和 Dániel Virosztek。 “量子位状态空间上的量子 Wasserstein 等距”。 J.马斯。 肛门。 应用。 522, 126955 (2023)。
https://doi.org/10.1016/j.jmaa.2022.126955
[52] Lu Li、Kaifeng Bu、Dax Enshan Koh、Arthur Jaffe 和 Seth Lloyd。 “量子电路的 Wasserstein 复杂性”。 arXiv:2208.06306(2022)。
https://doi.org/10.48550/arXiv.2208.06306
[53] 博巴克·图西·基亚尼、贾科莫·德·帕尔马、米拉德·马维安、刘子文和塞斯·劳埃德。 “通过量子推土机的距离学习量子数据”。 量子科学。 技术。 7、045002(2022)。
https://doi.org/10.1088/2058-9565/ac79c9
[54] EP Wigner 和 Mutsuo M. Yanase。 “分发的信息内容”。 过程。 国家。 阿卡德。 科学。 美国 49, 910–918 (1963)。
https:/ / doi.org/ 10.1073 / pnas.49.6.910
[55] Ryszard Horodecki、Paweł Horodecki、Michał Horodecki 和 Karol Horodecki。 “量子纠缠”。 牧师国防部。 物理。 81, 865–942 (2009)。
https:/ / doi.org/ 10.1103 / RevModPhys.81.865
[56] Otfried Gühne 和 Géza Tóth。 “纠缠检测”。 物理。 众议员 474, 1–75 (2009)。
https:///doi.org/10.1016/j.physrep.2009.02.004
[57] Nicolai Friis、Giuseppe Vitagliano、Mehul Malik 和 Marcus Huber。 “从理论到实验的纠缠证明”。 纳特。 物理学家。 1, 72–87 (2019)。
https://doi.org/10.1038/s42254-018-0003-5
[58] Vittorio Giovannetti、Seth Lloyd 和 Lorenzo Maccone。 “量子增强测量:超越标准量子极限”。 科学 306, 1330–1336 (2004)。
https:/ / doi.org/ 10.1126 / science.1104149
[59] 马特奥·GA 巴黎。 “量子技术的量子估计”。 国际。 J. Quant. 信息。 07, 125–137 (2009)。
https:/ / doi.org/ 10.1142 / S0219749909004839
[60] 拉法尔·德姆科维奇-多布赞斯基、马尔辛·贾日纳和扬·科洛丁斯基。 “第四章——光学干涉测量中的量子极限”。 程序。 光学 60, 345 – 435 (2015)。 arXiv:1405.7703。
https:///doi.org/10.1016/bs.po.2015.02.003
的arXiv:1405.7703
[61] 卢卡·佩兹和奥古斯托·斯梅尔齐。 “相位估计的量子理论”。 GM Tino 和 MA Kasevich,编辑,原子干涉测量法(Proc. Int. 物理学院“Enrico Fermi”,课程 188,瓦伦纳)。 第 691–741 页。 IOS 出版社,阿姆斯特丹(2014 年)。 arXiv:1411.5164。
的arXiv:1411.5164
[62] 盖萨·托特和德内斯·佩茨。 “方差的极值性质和量子费希尔信息”。 物理。 修订版 A 87, 032324 (2013)。
https:/ / doi.org/ 10.1103 / PhysRevA.87.032324
[63] 思夏于。 “量子费希尔信息作为方差的凸屋顶”。 arXiv:1302.5311(2013)。
https://doi.org/10.48550/arXiv.1302.5311
的arXiv:1302.5311
[64] 盖萨·托特和弗洛里安·弗洛维斯。 “基于密度矩阵凸分解的方差和量子费希尔信息的不确定性关系”。 物理。 修订版研究 4, 013075 (2022)。
https:/ / doi.org/ 10.1103 / PhysRevResearch.4.013075
[65] Shao-Hen Chiew 和曼努埃尔·盖斯纳。 “利用量子费希尔信息改善总不确定性关系”。 物理。 修订版研究 4, 013076 (2022)。
https:/ / doi.org/ 10.1103 / PhysRevResearch.4.013076
[66] CW 赫尔斯特罗姆。 “量子探测与估计理论”。 学术出版社,纽约。 (1976)。 网址:www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5。
https://www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5
[67] 作为霍莱沃。 “量子理论的概率和统计方面”。 北荷兰省,阿姆斯特丹。 (1982)。
[68] Samuel L. Braunstein 和 Carlton M. Caves。 “统计距离和量子态几何”。 物理。 牧师莱特。 72, 3439–3443 (1994)。
https:/ / doi.org/ 10.1103 / PhysRevLett.72.3439
[69] 塞缪尔·L·布劳恩斯坦、卡尔顿·M·卡夫斯和杰拉德·J·米尔本。 “广义不确定性关系:理论、例子和洛伦兹不变性”。 安. 物理。 247, 135–173 (1996)。
https:/ / doi.org/ 10.1006 / aphy.1996.0040
[70] 德内斯·佩茨。 “量子信息论和量子统计”。 施普林格、柏林、海德堡。 (2008)。
https://doi.org/10.1007/978-3-540-74636-2
[71] Géza Tóth 和 Iagoba Apellaniz。 “量子信息科学视角下的量子计量学”。 J.物理学。 答:数学。 理论。 47, 424006 (2014)。
https://doi.org/10.1088/1751-8113/47/42/424006
[72] Luca Pezzè、Augusto Smerzi、Markus K. Oberthaler、Roman Schmied 和 Philipp Treutlein。 “具有原子系综非经典状态的量子计量学”。 牧师国防部。 物理。 90, 035005 (2018)。
https:/ / doi.org/ 10.1103 / RevModPhys.90.035005
[73] 马可·巴比耶里。 “光量子计量学”。 PRX 量子 3, 010202 (2022)。
https:/ / doi.org/ 10.1103 / PRXQuantum.3.010202
[74] 佐尔坦·莱卡和德内斯·佩茨。 “矩阵方差的一些分解”。 很可能。 数学。 国家主义者。 33、191-199(2013)。 arXiv:1408.2707。
的arXiv:1408.2707
[75] 德内斯·佩茨和丹尼尔·维罗兹泰克。 “矩阵方差的表征定理”。 科学学报。 数学。 (塞格德)80, 681–687 (2014)。
https://doi.org/10.14232/actasm-013-789-z
[76] 藤原昭夫和今井宏。 “多个量子通道上的光纤束及其在量子统计中的应用”。 J. Phys。 答:数学。 理论。 41, 255304 (2008)。
https://doi.org/10.1088/1751-8113/41/25/255304
[77] BM Escher、RL de Matos Filho 和 L. Davidovich。 “估计噪声量子增强计量学最终精度极限的通用框架”。 纳特。 物理。 7、406-411(2011)。
https:/ / doi.org/ 10.1038 / nphys1958
[78] Rafał Demkowicz-Dobrzański、Jan Kołodyński 和 Mădălin Guţă。 “量子增强计量学中难以捉摸的海森堡极限”。 纳特。 交流。 3、1063(2012)。
https:///doi.org/10.1038/ncomms2067
[79] 伊曼·马尔维安. “量子热力学中量子渔夫信息的操作解释”。 物理。 莱特牧师。 129, 190502 (2022)。
https:/ / doi.org/ 10.1103 / PhysRevLett.129.190502
[80] 莱因哈德·F·维尔纳 (Reinhard F. Werner) “具有爱因斯坦-波多尔斯基-罗森相关性的量子态承认隐变量模型”。 物理。 修订版 A 40, 4277–4281 (1989)。
https:/ / doi.org/ 10.1103 / PhysRevA.40.4277
[81] K.埃克特、J.施利曼、D.布鲁斯和M.莱文斯坦。 “不可区分粒子系统中的量子相关性”。 安. 物理。 299, 88–127 (2002)。
https:/ / doi.org/ 10.1006 / aphy.2002.6268
[82] 市川翼、佐佐木敏彦、筒井泉、米泽信宏。 “交换对称性和多方纠缠”。 物理。 修订版 A 78, 052105 (2008)。
https:/ / doi.org/ 10.1103 / PhysRevA.78.052105
[83] 帕维尔·霍洛德茨基. “可分离性准则和具有正部分转置的不可分离混合态”。 物理。 莱特。 A 232, 333–339 (1997)。
https://doi.org/10.1016/S0375-9601(97)00416-7
[84] 亚瑟佩雷斯。 “密度矩阵的可分离性准则”。 物理。 牧师莱特。 77, 1413–1415 (1996)。
https:/ / doi.org/ 10.1103 / PhysRevLett.77.1413
[85] 帕韦乌·霍洛德茨基、米哈乌·霍洛德茨基和里斯扎德·霍洛德茨基。 “束缚纠缠可以被激活”。 物理。 莱特牧师。 82、1056-1059(1999)。
https:/ / doi.org/ 10.1103 / PhysRevLett.82.1056
[86] 盖萨·托特和塔马斯·维特西。 “具有正部分转置的量子态对于计量学很有用”。 物理。 莱特牧师。 120, 020506 (2018)。
https:/ / doi.org/ 10.1103 / PhysRevLett.120.020506
[87] 斯科特·希尔和威廉·K·伍特斯。 “一对量子位的纠缠”。 物理。 莱特牧师。 78, 5022–5025 (1997)。
https:/ / doi.org/ 10.1103 / PhysRevLett.78.5022
[88] 威廉·K·伍特斯。 “两个量子位的任意状态形成的纠缠”。 物理。 牧师莱特。 80, 2245–2248 (1998)。
https:/ / doi.org/ 10.1103 / PhysRevLett.80.2245
[89] David P. DiVincenzo、Christopher A. Fuchs、Hideo Mabuchi、John A. Smolin、Ashish Thapliyal 和 Armin Uhlmann。 “援助的纠缠”。 Quant-ph/9803033 (1998)。
https://doi.org/10.48550/arXiv.quant-ph/9803033
arXiv:quant-ph / 9803033
[90] 约翰·A·斯莫林、弗兰克·维斯特拉特和安德烈亚斯·温特。 “援助的纠缠与多方国家的蒸馏”。 物理。 修订版 A 72, 052317 (2005)。
https:/ / doi.org/ 10.1103 / PhysRevA.72.052317
[91] 霍尔格·霍夫曼 (Holger F. Hofmann) 和竹内茂树 (Shigeki Takeuchi)。 “违反局部不确定性关系作为纠缠的标志”。 物理。 修订版 A 68, 032103 (2003)。
https:/ / doi.org/ 10.1103 / PhysRevA.68.032103
[92] 奥特弗里德·古内。 “通过不确定性关系来表征纠缠”。 物理。 莱特牧师。 92, 117903 (2004)。
https:/ / doi.org/ 10.1103 / PhysRevLett.92.117903
[93] 奥特弗里德·居内、马蒂亚斯·梅赫勒、盖扎·托特和彼得·亚当。 “基于局部不确定性关系的纠缠准则严格强于可计算的交叉范数准则”。 物理。 修订版 A 74, 010301 (2006)。
https:/ / doi.org/ 10.1103 / PhysRevA.74.010301
[94] Giuseppe Vitagliano、Philipp Hyllus、Iñigo L. Egusquiza 和 Géza Tóth。 “任意自旋的自旋挤压不等式”。 物理。 牧师莱特。 107, 240502 (2011)。
https:/ / doi.org/ 10.1103 / PhysRevLett.107.240502
[95] AR埃德蒙兹。 “量子力学中的角动量”。 普林斯顿大学出版社。 (1957)。
https:/ / doi.org/10.1515/ 9781400884186
[96] 盖扎·托特。 “通过集体测量对玻色子原子的光学晶格进行纠缠检测”。 物理。 修订版 A 69, 052327 (2004)。
https:/ / doi.org/ 10.1103 / PhysRevA.69.052327
[97] Géza Tóth、Christian Knapp、Otfried Gühne 和 Hans J. Briegel。 “最佳自旋挤压不等式检测自旋模型中的束缚纠缠”。 物理。 牧师莱特。 99, 250405 (2007)。
https:/ / doi.org/ 10.1103 / PhysRevLett.99.250405
[98] 盖萨·托特和摩根·W·米切尔。 “原子系综中宏观单线态的生成”。 新物理学杂志。 12、053007(2010)。
https://doi.org/10.1088/1367-2630/12/5/053007
[99] 盖萨·托特。 “对称迪克态附近多部分纠缠的检测”。 J. 选择。 苏克。 是。 B 24, 275–282 (2007)。
https:/ / doi.org/ 10.1364 / JOSAB.24.000275
[100] 盖萨·托特、托比亚斯·莫罗德尔和奥特弗里德·古内。 “评估凸屋顶纠缠措施”。 物理。 莱特牧师。 114, 160501 (2015)。
https:/ / doi.org/ 10.1103 / PhysRevLett.114.160501
[101] 利文·范登伯格和斯蒂芬·博伊德。 “半定规划”。 暹罗评论 38, 49–95 (1996)。
https:/ / doi.org/10.1137/ 1038003
[102] 盖扎·托特。 “多方纠缠与高精度计量”。 物理。 修订版 A 85, 022322 (2012)。
https:/ / doi.org/ 10.1103 / PhysRevA.85.022322
[103] Philipp Hyllus、Wiesław Laskowski、Roland Krischek、Christian Schwemmer、Witlef Wieczorek、Harald Weinfurter、Luca Pezzé 和 Augusto Smerzi。 “Fisher 信息和多粒子纠缠”。 物理。 修订版 A 85, 022321 (2012)。
https:/ / doi.org/ 10.1103 / PhysRevA.85.022321
[104] 盖扎·托特 (Géza Tóth)、塔马斯·维特西 (Tamás Vértesi)、帕韦乌·霍洛德茨基 (Paweł Horodecki) 和里斯扎德·霍洛德茨基 (Ryszard Horodecki)。 “激活隐藏的计量有用性”。 物理。 莱特牧师。 125, 020402 (2020)。
https:/ / doi.org/ 10.1103 / PhysRevLett.125.020402
[105] AC Doherty、Pablo A. Parrilo 和 Federico M. Spedalieri。 “区分可分离态和纠缠态”。 物理。 莱特牧师。 88、187904(2002)。
https:/ / doi.org/ 10.1103 / PhysRevLett.88.187904
[106] 安德鲁·C·多尔蒂、巴勃罗·A·帕里洛和费德里科·M·斯佩达里里。 “完整的可分离性标准系列”。 物理。 修订版 A 69, 022308 (2004)。
https:/ / doi.org/ 10.1103 / PhysRevA.69.022308
[107] 安德鲁·C·多尔蒂、巴勃罗·A·帕里洛和费德里科·M·斯佩达里里。 “检测多方纠缠”。 物理。 修订版 A 71, 032333 (2005)。
https:/ / doi.org/ 10.1103 / PhysRevA.71.032333
[108] Harold Ollivier 和 Wojciech H. Zurek。 “量子不和谐:相关性的量子性度量”。 物理。 牧师莱特。 88, 017901 (2001)。
https:/ / doi.org/ 10.1103 / PhysRevLett.88.017901
[109] L.亨德森和V.维德拉尔。 “经典、量子和总相关性”。 J. Phys。 答:数学。 Gen. 34, 6899 (2001)。
https://doi.org/10.1088/0305-4470/34/35/315
[110] Anindita Bera、Tamoghna Das、Debasis Sadhukhan、Sudipto Singha Roy、Aditi Sen(De) 和 Ujjwal Sen。“量子不和谐及其盟友:对最近进展的回顾”。 代表程序。 物理。 81, 024001 (2017)。
https:///doi.org/10.1088/1361-6633/aa872f
[111] 德内斯·佩茨。 “量子力学中的协方差和费希尔信息”。 J. Phys。 答:数学。 Gen. 35, 929 (2002)。
https://doi.org/10.1088/0305-4470/35/4/305
[112] 保罗·吉比利斯科、日合文雄和德内斯·佩茨。 “量子协方差、量子费希尔信息和不确定性关系”。 IEEE 传输。 信息。 理论 55, 439–443 (2009)。
https:///doi.org/10.1109/TIT.2008.2008142
[113] D. Petz 和 C. Ghinea。 “量子费希尔信息简介”。 第 27 卷,第 261-281 页。 世界科学。 (2011)。
https:/ / doi.org/ 10.1142 / 9789814338745_0015
[114] 弗兰克·汉森. “公制调整后的偏差信息”。 过程。 国家。 阿卡德。 科学。 美国 105, 9909–9916 (2008)。
https:/ / doi.org/ 10.1073 / pnas.0803323105
[115] 保罗·吉比利斯科、达维德·吉罗拉米和弗兰克·汉森。 “通过度量调整偏斜信息来实现局部量子不确定性和干涉功率的统一方法”。 熵 23, 263 (2021)。
https:///doi.org/10.3390/e23030263
[116] MATLAB。 “9.9.0.1524771(r2020b)”。 MathWorks Inc. 马萨诸塞州内蒂克 (2020)。
[117] MOSEK ApS。 “用于 MATLAB 的 MOSEK 优化工具箱手册。 版本 9.0”。 (2019)。 网址:docs.mosek.com/9.0/toolbox/index.html。
https:///docs.mosek.com/9.0/toolbox/index.html
[118] J.洛夫伯格。 “YALMIP:MATLAB 中的建模和优化工具箱”。 CACSD 会议记录。 台湾台北(2004 年)。
[119] 盖萨·托特。 “QUBIT4MATLAB V3.0:用于 MATLAB 的量子信息科学和量子光学程序包”。 计算。 物理。 交流。 179, 430–437 (2008)。
https:///doi.org/10.1016/j.cpc.2008.03.007
[120] QUBIT4MATLAB 软件包可在 https://www.mathworks.com/matlabcentral/fileexchange/8433 和个人主页 https://gtoth.eu/qubit4matlab.html 上获取。
https://www.mathworks.com/matlabcentral/fileexchange/8433
被引用
[1] Laurent Lafleche,“量子最优传输和弱拓扑”, 的arXiv:2306.12944, (2023).
以上引用来自 SAO / NASA广告 (最近成功更新为2023-10-16 14:47:44)。 该列表可能不完整,因为并非所有发布者都提供合适且完整的引用数据。
无法获取 Crossref引用的数据 在上一次尝试2023-10-16 14:47:42期间:无法从Crossref获取10.22331 / q-2023-10-16-1143的引用数据。 如果DOI是最近注册的,这是正常的。
该论文发表在《量子》杂志上 国际知识共享署名署名4.0(CC BY 4.0) 执照。 版权归原始版权持有者所有,例如作者或其所在机构。
- :具有
- :是
- :不是
- ][p
- $UP
- 003
- 07
- 1
- 10
- 100
- 102
- 107
- 11
- 110
- 116
- 118
- 12
- 125
- 13
- 14
- 15%
- 150
- 16
- 17
- 178
- 179
- 19
- 1994
- 1996
- 1998
- 1999
- 20
- 2001
- 2005
- 2006
- 2008
- 2010
- 2011
- 2012
- 2013
- 2014
- 2015
- 2016
- 2017
- 2018
- 2019
- 2020
- 2021
- 2022
- 2023
- 22
- 23
- 24
- 247
- 25
- 26
- 27
- 28
- 29
- 2D
- 30
- 31
- 32
- 33
- 35%
- 36
- 39
- 40
- 41
- 46
- 49
- 50
- 51
- 52
- 53
- 54
- 58
- 60
- 65
- 66
- 67
- 7
- 70
- 72
- 73
- 75
- 77
- 8
- 80
- 84
- 87
- 9
- 90
- 91
- 97
- 98
- a
- 以上
- 摘要
- 学者
- ACCESS
- 活性
- Adam
- 调整
- 进步
- 对抗
- 背景
- 再次
- 算法
- 所有类型
- 已经
- 还
- 替代
- 时刻
- am
- 阿姆斯特丹
- an
- 分析
- 和
- 安德鲁
- 另一个
- 应用领域
- 应用领域
- 的途径
- 保健
- 阿瑟
- AS
- 阿谢尔
- 方面
- 帮助
- At
- 原子
- 尝试
- 作者
- 作者
- 可使用
- 平均
- b
- 当前余额
- 基于
- BE
- 成为
- 很
- 柏林
- 之间
- 界
- 大脑
- 午休
- 布达佩斯
- 种子套餐
- by
- 剑桥
- CAN
- 可以得到
- 进行
- 案件
- Center
- 中央
- 中心
- 证书
- 通道
- 特点
- 查理
- 便宜
- 克里斯托弗
- 城市
- 城市
- 分类
- 集体
- 如何
- COMM
- 评论
- 共享
- 完成
- 复杂
- 一台
- 计算机科学
- 研讨会 首页
- 分享链接
- 已联繫
- 建设
- 消费
- 包含
- Contents
- 捐款
- 收敛
- 凸
- 版权
- 相关
- 相应
- 价格
- 可以
- 对口
- 国家
- 课程
- 标准
- USB和Thunderbolt Cross
- data
- 数据科学
- David
- 定义
- 定义
- 延迟
- 它
- 密度
- 详细
- 检测
- 检测
- 不同
- 方向
- 不和
- 讨论
- 距离
- 分配
- 分布
- do
- 驾驶
- 滴
- ,我们将参加
- e
- Ë&T
- 每
- 地球
- 容易
- 经济学
- 编辑
- 努力
- el
- 工程师
- 一样
- 等于
- 方程
- 埃里克
- 本质上
- 评估
- 估计
- 醚(ETH)
- 甚至
- 日常
- 检查
- 检查
- 例子
- 异国情调
- 期望
- 实验
- 延长
- 家庭
- 家庭
- 著名
- 远
- 费德里科
- 部分
- 字段
- 找到最适合您的地方
- 寻找
- 流
- 针对
- 申请
- 训练
- 发现
- 基金会
- Foundations
- 四
- 骨架
- 坦率
- Free
- 止
- 汽油
- 功能
- 实用
- 根本
- 差距
- 根
- 其他咨询
- 生成的
- 生成对抗网络
- 几何
- 杰拉德
- 得到
- 图形
- 团队
- 哈罗德
- 哈佛
- 有
- 老旧房屋
- 丘陵
- 持有人
- 主页
- 创新中心
- HTML
- HTTP
- HTTPS
- i
- IEEE
- if
- ii
- 图片
- 图像分类
- 图片
- 想像
- 同步成像
- 伊曼
- in
- 公司
- 不平等
- 不等式
- 信息
- 信息
- 例
- 研究所
- 机构
- 有趣
- 国际
- 解释
- 介绍
- 介绍
- iOS
- IT
- 它的
- 本身
- 一月三十一日
- JavaScript的
- John
- 日志
- 旅程
- 吻
- 纳普
- 名:
- 劳伦斯
- 学习用品
- 学习
- 离开
- 阅读
- 李
- 让
- li
- 执照
- 生活
- 极限
- 范围
- Line
- 液体肥产线
- 清单
- 本地
- 看
- 离
- 机
- 机器学习
- 杂志
- 颠覆性技术
- 手册
- 许多
- 地图
- 地图
- 马尔科
- 马库斯
- 马丁
- 质量
- 美国马萨诸塞州
- 群众
- 数学
- 数学
- 矩阵
- 最大宽度
- 可能..
- 意味着
- 衡量
- 测量
- 措施
- 机械学
- 医生
- 医学影像
- 提到
- 公
- 指标
- 度量衡学
- 可能
- 最小化
- 杂
- 模型
- 造型
- 模型
- 动力泉源
- 月
- 更多
- 摩根
- 移动
- 移动
- 神秘
- 需求
- 网络
- 神经
- 全新
- 纽约
- 下页
- 诺贝尔获奖者
- 正常
- 概念
- 获得
- 十月
- of
- on
- 一
- 打开
- 运营
- 光学
- 最佳
- 优化
- or
- 秩序
- 原版的
- 其他名称
- 我们的
- 输出
- 超过
- 巴勃罗
- 包
- 包
- 页
- 网页
- 对
- 保罗
- 纸类
- 巴黎
- 地形公园
- 保罗
- 个人
- 透视
- 彼得
- 相
- PHIL
- 物理
- 地方
- 柏拉图
- 柏拉图数据智能
- 柏拉图数据
- 播放
- PO
- 积极
- 可能
- 功率
- 平台精度
- 当下
- express
- 普林斯顿
- 可能性
- 市场问题
- PROC
- Proceedings
- 过程
- 过程
- 处理
- 曲目
- 代码编程
- 进展
- 财产
- 提供
- 出版
- 发行人
- 出版商
- 二次的
- 如
- 量
- 数量
- 量子
- 量子纠缠
- 量子信息
- 量子力学
- 量子光学
- 量子物理学
- 量子系统
- 量子技术
- 量子比特
- 量子比特
- R
- 价格表
- 宁
- 真实
- 最近
- 最近
- 引用
- 反映
- 而不管
- 政权
- 在相关机构注册的
- 有关
- 关系
- 相对的
- 遗迹
- 表示
- 研究
- 限制
- 成果
- 返回
- 检讨
- 路
- 罗兰
- 角色
- 天台
- 罗伊
- 皇族
- s
- Sam
- 圣
- SAND
- 对工资盗窃
- 学校
- SCI
- 科学
- 科学
- .
- 斯科特
- 似乎
- 感
- 敏感
- 套数
- 形状
- 暹
- 信号
- 签名
- 歪斜
- 小
- 固体
- 太空
- 剩余名额
- 纺
- 标准
- 州/领地
- 州
- 统计
- 统计
- 斯蒂芬·
- 强
- 学习
- 顺利
- 这样
- 合适的
- 总和
- 系统
- 产品
- T
- 台湾
- 专业技术
- 告诉
- 模板
- 测试
- 测试
- 比
- 这
- 图
- 其
- 理论
- 博曼
- 他们
- Free Introduction
- 那些
- 时
- 标题
- 至
- 工具箱
- 合计
- 反
- 改造
- 运输
- 交通运输或是
- 旅行
- 趋势
- 二
- 全功能包
- 不确定
- 下
- 相关
- 不幸
- 统一
- 大学
- 更新
- 网址
- us
- 运用
- 通常
- 变化
- 版本
- 非常
- 通过
- 重要
- 体积
- 的
- W
- 旺
- 想
- 是
- 方法..
- we
- 为
- ,尤其是
- 是否
- 这
- 而
- WHO
- 威廉
- 冬季
- 工作
- 世界
- X
- 年
- 但
- 纽约
- 和风网
- 零
- 张