[Дзеркало] Програми квадратичної арифметики: від нуля до героя

Віталік Бутерін через в Блог Віталіка Бутеріна

Це дзеркало поста на https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

Останнім часом існує великий інтерес до технології, що лежить в основі zk-SNARK, і людей стає все більше намагаючись демістифікувати те, що багато хто називає «місячною математикою» через її сприйману абсолютну складність, яку неможливо розшифрувати. Зрозуміти zk-SNARK справді досить складно, особливо через величезну кількість рухомих частин, які мають об’єднатися, щоб усе запрацювало, але якщо ми розіб’ємо технологію по частинах, то зрозуміти її стане простіше.

Метою цієї публікації є не повне ознайомлення з zk-SNARK; він припускає, що базові знання (i) ви знаєте, що таке zk-SNARK і що вони роблять, і (ii) знаєте достатньо математики, щоб мати можливість міркувати про такі речі, як поліноми (якщо твердження �(�)+�(�) =(�+�)(�) , де � і � — поліноми, здається вам природним і очевидним, тоді ви на правильному рівні). Скоріше, публікація глибше вивчає механізми, що стоять за технологією, і намагається якомога краще пояснити першу половину конвеєра, як намалював дослідник zk-SNARK Еран Тромер тут:

Тут кроки можна розбити на дві половини. По-перше, zk-SNARK не можна застосовувати безпосередньо до будь-якої обчислювальної задачі; скоріше, ви повинні перетворити проблему в правильну «форму», щоб проблема діяла. Форма називається «квадратичною арифметичною програмою» (QAP), і перетворення коду функції в одну з них є дуже нетривіальним. Разом із процесом перетворення коду функції на QAP існує ще один процес, який можна запустити, щоб, якщо у вас є вхідні дані для коду, ви могли створити відповідне рішення (іноді його називають «свідком» QAP). Після цього існує ще один досить складний процес для створення фактичного «доказу нульового знання» для цього свідка та окремий процес для перевірки доказу, який хтось інший передає вам, але це деталі, які виходять за межі цієї публікації. .

Приклад, який ми виберемо, є простим: доказ того, що ви знаєте розв’язок кубічного рівняння: �3+�+5=35 (підказка: відповідь 3). Ця проблема досить проста, тому кінцевий QAP не буде настільки великим, щоб лякати, але досить нетривіальною, щоб ви могли бачити, як усі механізми вступають у дію.

Запишемо нашу функцію так:

def qeval(x):
    y = x**3
    return x + y + 5

Проста мова програмування спеціального призначення, яку ми тут використовуємо, підтримує базову арифметику (+, −, ⋅, /), піднесення до степеня (�7, але не ��) і присвоювання змінних, що є досить потужним, щоб ви могли теоретично це зробити. будь-які обчислення всередині нього (за умови, що кількість кроків обчислення обмежена; цикли не допускаються). Зауважте, що оператори за модулем (%) і порівняння (<, >, ≤, ≥) НЕ підтримуються, оскільки немає ефективного способу виконати за модулем або порівняння безпосередньо в арифметиці скінченної циклічної групи (будьте вдячні за це; якщо був спосіб щоб виконати будь-яке з них, криптографія еліптичної кривої буде зламана швидше, ніж ви можете сказати «двійковий пошук» і «китайська теорема про залишки»).

Ви можете розширити мову до модулів і порівнянь, забезпечивши розкладання бітів (наприклад, 13=23+22+1) як допоміжні вхідні дані, підтвердивши правильність цих розкладів і виконуючи математику в двійкових схемах; в арифметиці скінченних полів виконання перевірок на рівність (==) також можливо і насправді трохи простіше, але це обидві деталі, які ми не будемо розглядати зараз. Ми можемо розширити мову для підтримки умов (наприклад, якщо �<5:�=7; інакше: �=9), перетворивши їх в арифметичну форму: �=7⋅(�<5)+9⋅(�≥5 ), однак зауважте, що обидва «шляхи» умовного виразу повинні бути виконані, і якщо у вас багато вкладених умовних виразів, це може призвести до великої кількості накладних витрат.

Давайте тепер пройдемо цей процес крок за кроком. Якщо ви хочете зробити це самостійно для будь-якого фрагмента коду, я тут реалізовано компілятор (тільки для освітніх цілей; ще не готовий до створення QAP для реальних zk-SNARK!).

Уплощение

Першим кроком є ​​процедура «зведення», під час якої ми перетворюємо вихідний код, який може містити як завгодно складні оператори та вирази, у послідовність операторів двох форм: �=� (де � може бути змінною або числом ) і �=� (��) � (де �� може бути +, −, ⋅, /, а � і � можуть бути змінними, числами або самими підвиразами). Ви можете розглядати кожне з цих тверджень як щось на зразок логічних воріт у схемі. Результат процесу зведення для наведеного вище коду такий:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

Якщо ви прочитаєте оригінальний код і код тут, ви можете досить легко побачити, що вони еквівалентні.

Ворота до R1CS

Тепер ми перетворюємо це на так звану систему обмежень рангу 1 (R1CS). R1CS — це послідовність груп із трьох векторів (�, �, �), а розв’язком R1CS є вектор �, де � повинен задовольняти рівнянню �.�⋅�.�−�.�=0, де . являє собою скалярний добуток – простіше кажучи, якщо ми «з’єднуємо» � і �, помноживши два значення в однакових позиціях, а потім беремо суму цих добутків, потім робимо те саме з � і �, а потім � і � , то третій результат дорівнює добутку перших двох результатів. Наприклад, це задоволений R1CS:

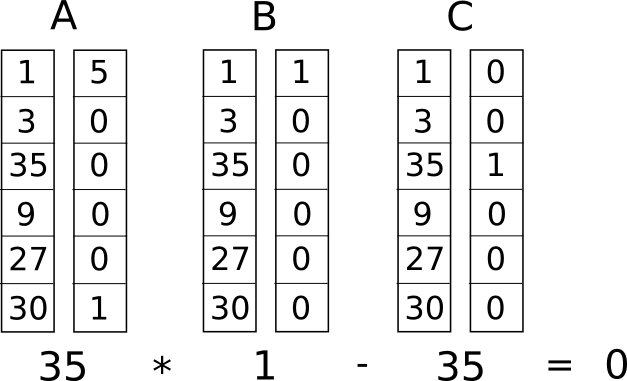
Але замість того, щоб мати лише одне обмеження, ми матимемо багато обмежень: по одному для кожного логічного вентиля. Існує стандартний спосіб перетворення логічних воріт на (�,�,�) трійку залежно від того, якою є операція (+, −, ⋅ або /) і чи є аргументи змінними чи числами. Довжина кожного вектора дорівнює загальній кількості змінних у системі, включаючи фіктивну змінну ~one за першим індексом, що представляє число 1, вхідні змінні, фіктивну змінну ~out, що представляє вихід, а потім усі проміжні змінні (���1 і ���2 вище); вектори, як правило, будуть дуже розрідженими, лише заповнюючи слоти, що відповідають змінним, на які впливає певний логічний вентиль.

Спочатку ми надамо зіставлення змінних, які ми будемо використовувати:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

Вектор розв’язку складатиметься з присвоєння для всіх цих змінних у такому порядку.

Тепер ми дамо трійку (�,�,�) для перших воріт:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

Ви бачите, що якщо вектор розв’язку містить 3 у другій позиції та 9 у четвертій позиції, то незалежно від решти вмісту вектора розв’язку перевірка скалярного добутку зведеться до 3⋅3=9, і так і пройде. Якщо вектор розв’язку має −3 у другій позиції та 9 у четвертій позиції, перевірка також пройде; фактично, якщо вектор розв’язку має 7 у другій позиції та 49 у четвертій позиції, тоді ця перевірка все одно пройде — мета цієї першої перевірки полягає в тому, щоб перевірити узгодженість входів і виходів лише першого вентиля.

А тепер переходимо до других воріт:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

Подібно до першої перевірки скалярного добутку, тут ми перевіряємо, що ���1⋅�=�.

Тепер треті ворота:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

Тут шаблон дещо інший: це множення першого елемента у векторі розв’язку на другий елемент, потім на п’ятий елемент, додавання двох результатів і перевірка, чи дорівнює сума шостому елементу. Оскільки перший елемент у векторі розв’язку завжди дорівнює одиниці, це лише перевірка додавання, яка перевіряє, що вихід дорівнює сумі двох вхідних даних.

Нарешті, четверті ворота:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

Тут ми оцінюємо останню перевірку, ~out =���2+5. Перевірка скалярного добутку працює так, що береться шостий елемент у векторі розв’язання, п’ять разів додається до першого елемента (нагадування: перший елемент дорівнює 1, тому це фактично означає додавання 5) і порівнюється з третім елементом, де ми зберегти вихідну змінну.

І ось у нас є наш R1CS із чотирма обмеженнями. Свідок — це просто призначення всім змінним, включаючи вхідні, вихідні та внутрішні змінні:

[1, 3, 35, 9, 27, 30]

Ви можете обчислити це самостійно, просто «виконавши» наведений вище зведений код, починаючи з призначення вхідної змінної �=3, і вводячи значення всіх проміжних змінних і виведення під час їх обчислення.

Повний R1CS разом:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS до QAP

Наступним кроком є ​​використання цього R1CS і перетворення його у форму QAP, яка реалізує ту саму логіку, за винятком використання поліномів замість скалярних добутків. Робимо це наступним чином. Ми переходимо від чотирьох груп із трьох векторів довжиною шість до шести груп із трьох поліномів третього ступеня, де оцінюємо поліноми на кожному координата x являє собою одне з обмежень. Тобто, якщо ми обчислюємо поліноми при �=1, то отримуємо перший набір векторів, якщо ми обчислюємо поліноми при �=2, то отримуємо другий набір векторів і так далі.

Ми можемо зробити це перетворення, використовуючи щось, що називається a Інтерполяція Лагранжа. Проблема, яку вирішує інтерполяція Лагранжа, полягає в наступному: якщо у вас є набір точок (тобто (�,�) пар координат), то виконання інтерполяції Лагранжа в цих точках дає вам поліном, який проходить через усі ці точки. Ми робимо це шляхом декомпозиції задачі: для кожної � координати ми створюємо поліном, який має бажану � координату на цій � координаті та � координату 0 на всіх інших � координатах, які нас цікавлять, а потім отримуємо кінцеву в результаті ми складаємо всі поліноми разом.

Давайте наведемо приклад. Припустімо, що нам потрібен поліном, який проходить через (1,3),(2,2) і (3,4). Ми починаємо зі створення полінома, який проходить через (1,3),(2,0) і (3,0). Як виявилося, легко створити поліном, який «стирчить» при �=1 і дорівнює нулю в інших точках інтересу; ми просто робимо:

(x - 2) * (x - 3)

Що виглядає так:

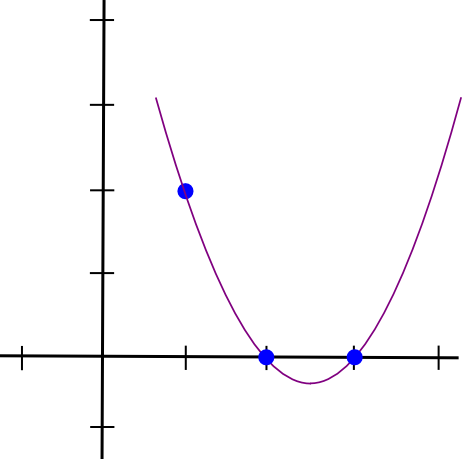
Тепер нам просто потрібно «перемасштабувати» його так, щоб висота на x=1 була правильною:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

Це дає нам:

1.5 * x**2 - 7.5 * x + 9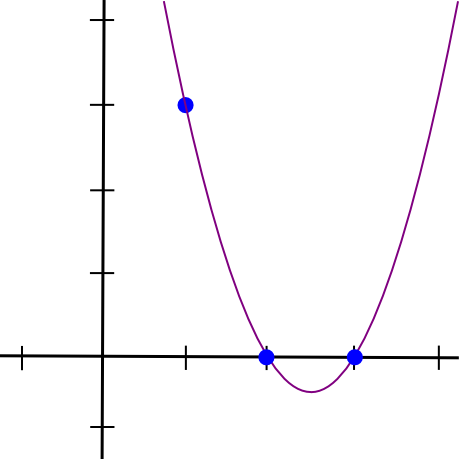

Потім ми робимо те ж саме з двома іншими точками й отримуємо два інші схожі на вигляд поліноми, за винятком того, що вони «стирчать» у �=2 і �=3 замість �=1. Складаємо всі три разом і отримуємо:

1.5 * x**2 - 5.5 * x + 7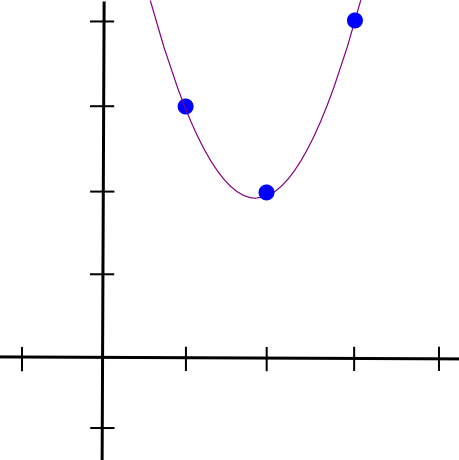

Саме з тими координатами, які ми хочемо. Алгоритм, описаний вище, займає �(�3) часу, оскільки є � точки, і кожна точка вимагає �(�2) часу, щоб помножити поліноми разом; якщо трохи подумати, цей час можна скоротити до �(�2) часу, а якщо ще більше подумати, використовуючи алгоритми швидкого перетворення Фур’є тощо, його можна скоротити ще більше — важлива оптимізація, коли функції, які використовуються в zk - SNARK на практиці часто мають багато тисяч воріт.

Тепер давайте використаємо інтерполяцію Лагранжа для перетворення нашого R1CS. Що ми збираємося зробити, так це взяти перше значення з кожного вектора �, використати інтерполяцію Лагранжа, щоб створити з нього поліном (де обчислення полінома в � дає вам перше значення �-го � вектора), повторити процес для першого значення кожного вектора � і �, а потім повторіть цей процес для других значень, третіх значень і так далі. Для зручності надам відповіді прямо зараз:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

Коефіцієнти розташовані в порядку зростання, тому перший поліном вище фактично дорівнює 0.833⋅�3—5⋅�2+9.166⋅�−5. Цей набір поліномів (плюс поліном Z, який я поясню пізніше) складає параметри для цього конкретного екземпляра QAP. Зауважте, що всю роботу до цього моменту потрібно виконувати лише один раз для кожної функції, яку ви намагаєтеся перевірити за допомогою zk-SNARK; як тільки параметри QAP будуть згенеровані, їх можна використовувати повторно.

Давайте спробуємо обчислити всі ці поліноми при �=1. Обчислення полінома при �=1 просто означає додавання всіх коефіцієнтів (як 1�=1 для всіх �), тому це не складно. Ми отримуємо:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

І ось, ми маємо те ж саме, що й набір із трьох векторів для перших логічних воріт, які ми створили вище.

Перевірка QAP

Тепер який сенс цієї божевільної трансформації? Відповідь полягає в тому, що замість того, щоб перевіряти обмеження в R1CS окремо, тепер ми можемо перевіряти усі обмеження одночасно шляхом перевірки скалярного добутку на поліномах.

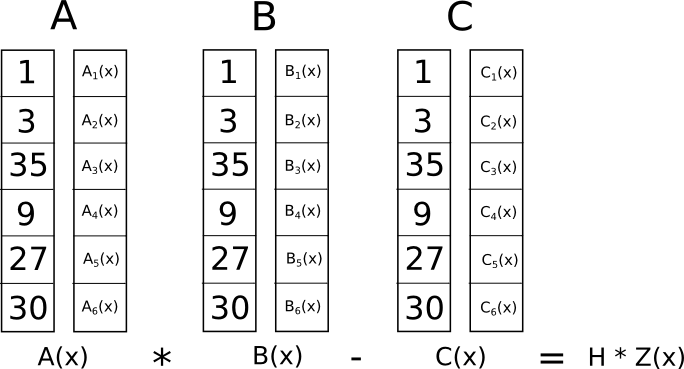
Оскільки в цьому випадку перевірка скалярного добутку є серією додавання та множення поліномів, результат сам по собі буде поліномом. Якщо отриманий поліном, обчислений на кожній координаті �, яку ми використовували вище для представлення логічного вентиля, дорівнює нулю, то це означає, що всі перевірки проходять; якщо результуючий поліном, обчислений принаймні за однією з координат �, що представляє логічний вентиль, дає ненульове значення, то це означає, що значення, що входять і виходять з цього логічного вентиля, є несумісними (тобто вентиль є �=�⋅�� �1, але надані значення можуть бути ����2=1 і �=2).

Зверніть увагу, що отриманий поліном сам по собі не повинен дорівнювати нулю, і насправді в більшості випадків таким не буде; він може мати будь-яку поведінку в точках, які не відповідають жодним логічним воротам, доки результат дорівнює нулю в усіх точках, які do відповідають деяким воротам. Щоб перевірити правильність, ми фактично не обчислюємо поліном �=�.�⋅�.�−�.� в кожній точці, що відповідає воротам; замість цього ми ділимо � на інший многочлен, �, і перевіряємо, що � рівномірно ділить � – тобто ділення �/� не залишає залишку.

� визначається як (�−1)⋅(�−2)⋅(�−3)… – найпростіший поліном, який дорівнює нулю в усіх точках, які відповідають логічним вентилям. Це елементарний факт алгебри, що будь-який поліном, який дорівнює нулю в усіх цих точках, повинен бути кратним цьому мінімальному поліному, і якщо поліном є кратним �, то його оцінка в будь-якій з цих точок буде нульовою; ця еквівалентність значно полегшує нашу роботу.

Тепер давайте перевіримо скалярний добуток із наведеними вище поліномами. По-перше, проміжні поліноми:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

Тепер �.�⋅�.�—�.�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

Тепер мінімальний поліном �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):

Z = [24, -50, 35, -10, 1]

І якщо ми розділимо результат вище на �, ми отримаємо:

h = t / Z = [-3.666, 17.055, -3.444]

Без залишку.

Отже, у нас є рішення для QAP. Якщо ми спробуємо фальсифікувати будь-яку зі змінних у рішенні R1CS, з якого ми отримуємо це рішення QAP — скажімо, встановити останню на 31 замість 30, тоді ми отримаємо поліном �, який не проходить одну з перевірок (зокрема, у випадку �=3 результат дорівнюватиме −1 замість 0), і, крім того, � не буде кратним �; скоріше ділення �/� дасть залишок [−5.0,8.833,−4.5,0.666].

Зауважте, що наведене вище є спрощенням; «У реальному світі» додавання, множення, віднімання та ділення відбуватимуться не зі звичайними числами, а з елементами скінченного поля — моторошним різновидом арифметики, яка є самоузгодженою, тому всі алгебраїчні закони, які ми знаємо й любимо, досі справедливо, але де всі відповіді є елементами деякої множини скінченного розміру, зазвичай цілими числами в діапазоні від 0 до �−1 для деякого �. Наприклад, якщо �=13, то 1/2=7 (а 7⋅2=1),3⋅5=2 і так далі. Використання арифметики кінцевих полів усуває необхідність турбуватися про помилки округлення та дозволяє системі добре працювати з еліптичними кривими, які в кінцевому підсумку є необхідними для решти механізмів zk-SNARK, які роблять протокол zk-SNARK фактично безпечним.

Особлива подяка Ерану Тромеру за допомогу в поясненні багатьох деталей внутрішньої роботи zk-SNARK.

• Розповсюдження контенту та PR на основі SEO. Отримайте посилення сьогодні.
• PlatoData.Network Vertical Generative Ai. Додайте собі сили. Доступ тут.
• PlatoAiStream. Web3 Intelligence. Розширення знань. Доступ тут.
• ПлатонЕСГ. вуглець, CleanTech, Енергія, Навколишнє середовище, Сонячна, Поводження з відходами. Доступ тут.
• PlatoHealth. Розвідка про біотехнології та клінічні випробування. Доступ тут.
• BlockOffsets. Модернізація екологічної компенсаційної власності. Доступ тут.
• джерело: Інформація про дані Платона.