Гаусівський наївний Байєс, пояснення

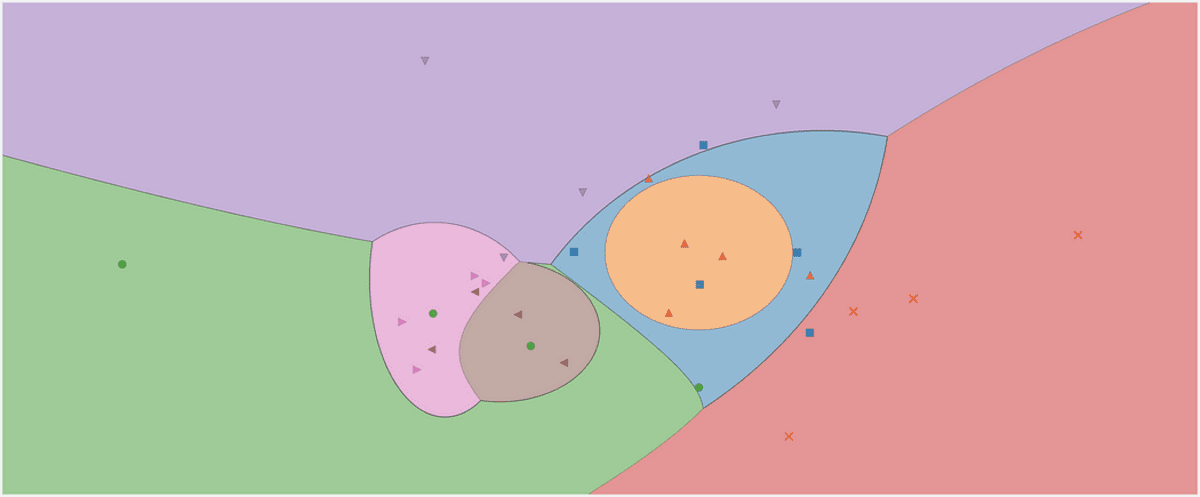
Область рішення гаусового наївного класифікатора Байєса. Зображення автора.

Я думаю, що це класика на початку кожної кар’єри в галузі обробки даних: Наївний байєсівський класифікатор. Або краще сказати, що сім'я наївних байєсівських класифікаторів, оскільки вони мають багато варіантів. Наприклад, існує мультиноміальний наївний класифікатор Байєса, наивний класифікатор Бернуллі, а також гаусівський наївний класифікатор Байєса, кожен з яких відрізняється лише однією маленькою деталлю, як ми з’ясуємо. Наївні алгоритми Байєса досить прості за дизайном, але виявилися корисними в багатьох складних ситуаціях реального світу.

У цій статті ви можете дізнатися

• як працюють наївні класифікатори Байєса,
• чому має сенс визначати їх такими, якими вони є, і
• як реалізувати їх у Python за допомогою NumPy.

Ви можете знайти код на мій Github.

Це може допомогти трохи перевірити мій букмекер про байєсівську статистику Лагідний вступ до байєсівського висновку щоб звикнути до формули Байєса. Оскільки ми реалізовуватимемо класифікатор у спосіб навчання, який відповідає scikit, також варто переглянути мою статтю Створіть власну регресію scikit-learn. Однак накладні витрати на scikit-learn досить невеликі, і ви все одно зможете слідувати.

Ми почнемо досліджувати напрочуд просту теорію наївної класифікації Байєса, а потім перейдемо до реалізації.

Що нас насправді цікавить під час класифікації? Що ми насправді робимо, який вхід і вихід? Відповідь проста:

Яка ймовірність того, що x належить до деякого класу c, задано точкою даних x?

Це все, що ми хочемо відповісти будь-який класифікація. Ви можете безпосередньо моделювати це твердження як умовну ймовірність: p(c|x).

Наприклад, якщо є

• Класи 3 c₁, c₂, c₃ та
• x складається з 2 особливостей x₁, x₂,

результатом класифікатора може бути щось подібне p(c₁|x₁, x₂)=0.3, p(c₂|x₁, x₂)=0.5 а p(c₃|x₁, x₂)=0.2. Якщо ми дбаємо про одну мітку як результат, ми виберемо ту з найвищою ймовірністю, тобто c₂ тут з імовірністю 50%.

Наївний класифікатор Байєса намагається безпосередньо обчислити ці ймовірності.

Наївні Баєси

Гаразд, дано точку даних x, ми хочемо обчислити p(c|x) для всіх класів c а потім виведіть c з найбільшою ймовірністю. У формулах ви часто бачите це як

Зображення автора.

Примітка: Макс p(c|x) повертає максимальну ймовірність, тоді як argmax p(c|x) повертає c з цією найвищою ймовірністю.

Але перш ніж ми зможемо оптимізувати p(c|x), ми повинні мати можливість це обчислити. Для цього використовуємо Теорема Байєса:

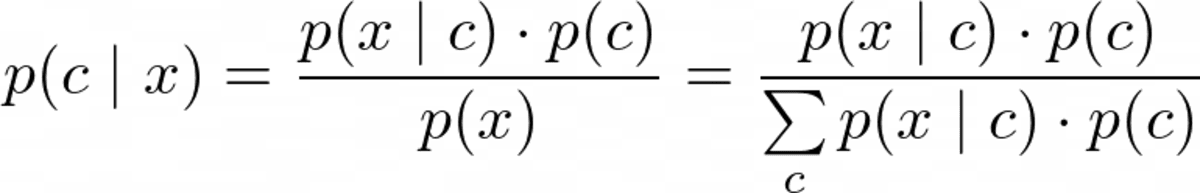
Теорема Байєса. Зображення автора.

Це частина наївного Байєса. Але зараз ми маємо таку проблему: що є p(x|c) і p(c)?

Ось у чому полягає навчання наївного класифікатора Байєса.

Навчання

Щоб проілюструвати все, скористаємося набором даних іграшки з дві реальні особливості x₁, x₂ та  три класи c₁, c₂, c₃ у наступному.

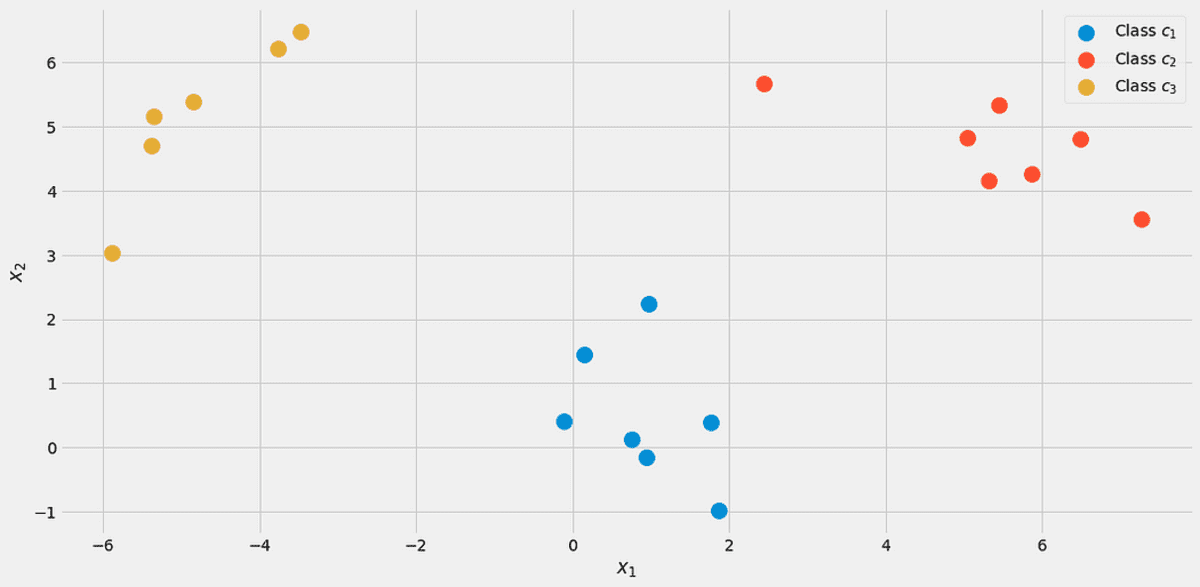
Дані візуалізовані. Зображення автора.

Ви можете створити цей точний набір даних за допомогою

from sklearn.datasets import make_blobs X, y = make_blobs(n_samples=20, centers=[(0,0), (5,5), (-5, 5)], random_state=0)

Почнемо з ймовірність класу p(c), ймовірність того, що деякий клас c спостерігається в позначеному наборі даних. Найпростіший спосіб оцінити це — просто обчислити відносні частоти класів і використовувати їх як ймовірності. Ми можемо використовувати наш набір даних, щоб побачити, що це означає.

7 із 20 балів позначено класом c₁ (синій) у наборі даних, тому ми кажемо p(c₁)=7/20. Маємо 7 балів за клас c₂ (червоний), тому ми встановлюємо p(c₂)=7/20. Останній клас c₃ (жовтий) має лише 6 балів, отже p(c₃)=6/20.

Це просте обчислення ймовірностей класу нагадує підхід максимальної правдоподібності. Однак ви також можете використовувати інший попередній розподіл, якщо хочете. Наприклад, якщо ви знаєте, що цей набір даних не є репрезентативним для справжньої сукупності, оскільки клас c₃ має з’являтися в 50% випадків, тоді ви встановлюєте p(c₁)=0.25, p(c₂)=0.25 а p(c₃)=0.5. Все, що допоможе вам покращити продуктивність тестового набору.

Тепер переходимо до ймовірність p(x|c)=p(x₁, x₂|c). Одним із підходів до обчислення цієї ймовірності є фільтрація набору даних для зразків із міткою c а потім спробуйте знайти розподіл (наприклад, 2-вимірний Гаусс), який фіксує особливості x₁, x₂.

На жаль, зазвичай ми не маємо достатньо зразків для класу, щоб правильно оцінити ймовірність.

Щоб створити більш надійну модель, ми робимо наївне припущення що особливості x₁, x₂ він має стохастично незалежні, дано c. Це лише дивовижний спосіб полегшити математику за допомогою

Зображення автора

для кожного класу c. Тут де наївний частина наївного Байєса походить з того, що це рівняння загалом не виконується. Проте навіть тоді наївний Байєс на практиці дає хороші, часом видатні результати. Багаточленний наївний Байєс сяє особливо для проблем НЛП із функціями сумки слів.

Наведені вище аргументи однакові для будь-якого простого класифікатора Байєса, який ви можете знайти. Тепер це залежить лише від того, як ви моделюєте p(x₁|c₁), p(x₂|c₁), p(x₁|c₂), p(x₂|c₂), p(x₁|c₃) та  p(x₂|cXNUMX).

Якщо ваші функції лише 0 і 1, ви можете використовувати a Розподіл Бернуллі. Якщо вони цілі числа, a Мультиноміальний розподіл. Однак ми маємо реальні значення характеристик і приймаємо рішення для a Гауссія розподілу, звідси назва гаусівського наївного Байєса. Приймемо наступний вигляд

Зображення автора.

де μᵢ,ⱼ є середнім і σᵢ,ⱼ це стандартне відхилення, яке ми маємо оцінити за даними. Це означає, що ми отримуємо одне середнє для кожної функції i у поєднанні з класом cⱼ, у нашому випадку 2*3=6 означає. Те саме стосується стандартних відхилень. Це вимагає прикладу.

Спробуємо оцінити μ₂,₁ та  σ₂,₁. Оскільки j=1, нас цікавить тільки клас c₁, дозвольте нам зберігати лише зразки з цією міткою. Залишилися такі зразки:

# samples with label = c_1 array([[ 0.14404357, 1.45427351], [ 0.97873798, 2.2408932 ], [ 1.86755799, -0.97727788], [ 1.76405235, 0.40015721], [ 0.76103773, 0.12167502], [-0.10321885, 0.4105985 ], [ 0.95008842, -0.15135721]])

Тепер через i=2 ми маємо розглянути лише другий стовпець. μ₂,₁ є середнім і σ₂,₁ стандартне відхилення для цього стовпця, тобто μ₂,₁ = 0.49985176 і σ₂,₁ = 0.9789976.

Ці цифри мають сенс, якщо знову поглянути на діаграму розсіювання зверху. Особливості x₂ зразків із класу c₁ приблизно 0.5, як видно на малюнку.

Зараз ми обчислюємо це для інших п’яти комбінацій, і готово!

У Python це можна зробити так:

from sklearn.datasets import make_blobs
import numpy as np # Create the data. The classes are c_1=0, c_2=1 and c_3=2.
X, y = make_blobs( n_samples=20, centers=[(0, 0), (5, 5), (-5, 5)], random_state=0
) # The class probabilities.
# np.bincounts counts the occurence of each label.
prior = np.bincount(y) / len(y) # np.where(y==i) returns all indices where the y==i.
# This is the filtering step.
means = np.array([X[np.where(y == i)].mean(axis=0) for i in range(3)])
stds = np.array([X[np.where(y == i)].std(axis=0) for i in range(3)])

Ми отримуємо

# priors
array([0.35, 0.35, 0.3 ])
# means array([[ 0.90889988, 0.49985176], [ 5.4111385 , 4.6491892 ], [-4.7841679 , 5.15385848]])
# stds
array([[0.6853714 , 0.9789976 ], [1.40218915, 0.67078568], [0.88192625, 1.12879666]])

Це результат навчання гауссового наївного класифікатора Байєса.

Складання прогнозів

Повна формула прогнозу така

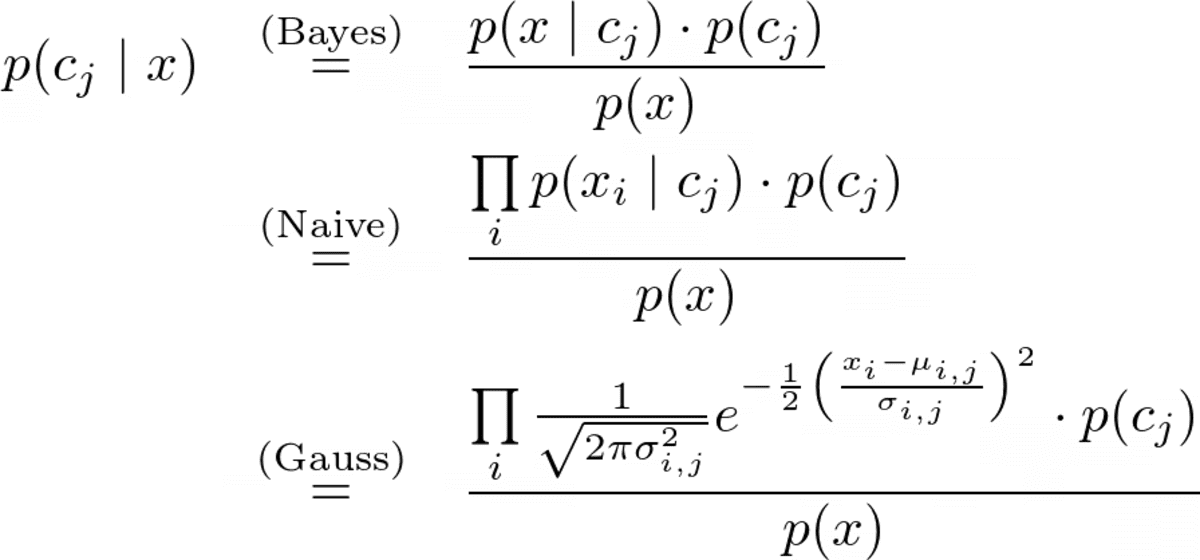
Зображення автора.

Припустімо нову точку даних x*=(-2, 5) входить.

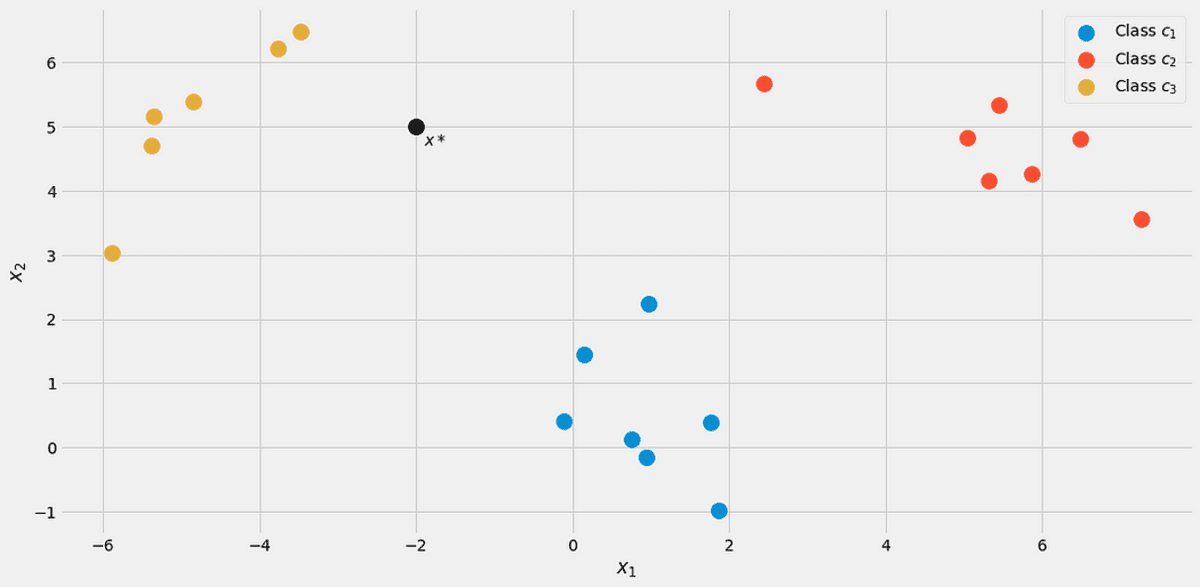
Зображення автора.

Щоб побачити, до якого класу він належить, обчислимо p(c|x*) для всіх класів. З малюнка це повинно належати до класу c₃ = 2, але подивимося. Знехтуймо знаменником p(x) на секунду. Використовуючи наступний цикл, обчислюємо номінатори для j = 1, 2, 3.

x_new = np.array([-2, 5]) for j in range(3): print( f"Probability for class {j}: {(1/np.sqrt(2*np.pi*stds[j]**2)*np.exp(-0.5*((x_new-means[j])/stds[j])**2)).prod()*p[j]:.12f}" )

Ми отримуємо

Probability for class 0: 0.000000000263
Probability for class 1: 0.000000044359
Probability for class 2: 0.000325643718

Звичайно, ці ймовірності (ми не повинні називати їх так) не додають до одиниці, оскільки ми проігнорували знаменник. Однак це не проблема, оскільки ми можемо просто взяти ці ненормалізовані ймовірності та розділити їх на суму, тоді вони складуть одиницю. Отже, поділивши ці три значення на їхню суму приблизно 0.00032569, ми отримаємо

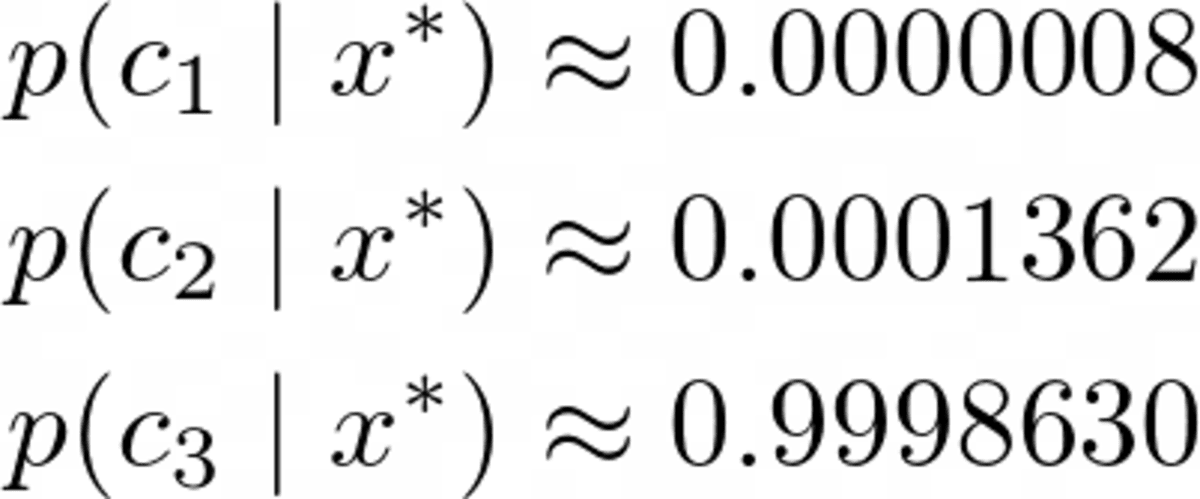
Зображення автора.

Явний переможець, як ми і очікували. А тепер давайте це реалізуємо!

Ця реалізація далеко не ефективна, чисельно не стабільна, вона служить лише для освітніх цілей. Ми обговорили більшість речей, тож слідкувати за цим має бути легко. Ви можете ігнорувати все check функцій або прочитайте мою статтю Створіть свій власний scikit-learn якщо вам цікаво, що саме вони роблять.

Просто зауважте, що я реалізував a predict_proba перший метод для обчислення ймовірностей. Метод predict просто викликає цей метод і повертає індекс (=клас) із найвищою ймовірністю за допомогою функції argmax (ось воно знову!). Клас чекає занять від 0 до k-1, де k – кількість класів.

import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted class GaussianNaiveBayesClassifier(BaseEstimator, ClassifierMixin): def fit(self, X, y): X, y = check_X_y(X, y) self.priors_ = np.bincount(y) / len(y) self.n_classes_ = np.max(y) + 1 self.means_ = np.array( [X[np.where(y == i)].mean(axis=0) for i in range(self.n_classes_)] ) self.stds_ = np.array( [X[np.where(y == i)].std(axis=0) for i in range(self.n_classes_)] ) return self def predict_proba(self, X): check_is_fitted(self) X = check_array(X) res = [] for i in range(len(X)): probas = [] for j in range(self.n_classes_): probas.append( ( 1 / np.sqrt(2 * np.pi * self.stds_[j] ** 2) * np.exp(-0.5 * ((X[i] - self.means_[j]) / self.stds_[j]) ** 2) ).prod() * self.priors_[j] ) probas = np.array(probas) res.append(probas / probas.sum()) return np.array(res) def predict(self, X): check_is_fitted(self) X = check_array(X) res = self.predict_proba(X) return res.argmax(axis=1)

Тестування реалізації

Незважаючи на те, що код досить короткий, він все ще занадто довгий, щоб бути повністю впевненими, що ми не зробили жодної помилки. Отже, давайте перевіримо, як це порівнюється з Класифікатор scikit-learn GaussianNB.

my_gauss = GaussianNaiveBayesClassifier()
my_gauss.fit(X, y)
my_gauss.predict_proba([[-2, 5], [0,0], [6, -0.3]])

виходи

array([[8.06313823e-07, 1.36201957e-04, 9.99862992e-01], [1.00000000e+00, 4.23258691e-14, 1.92051255e-11], [4.30879705e-01, 5.69120295e-01, 9.66618838e-27]])

Прогнози з використанням predict метод є

# my_gauss.predict([[-2, 5], [0,0], [6, -0.3]])
array([2, 0, 1])

Тепер скористаємося scikit-learn. Додавання коду

from sklearn.naive_bayes import GaussianNB gnb = GaussianNB()
gnb.fit(X, y)
gnb.predict_proba([[-2, 5], [0,0], [6, -0.3]])

врожайність

array([[8.06314158e-07, 1.36201959e-04, 9.99862992e-01], [1.00000000e+00, 4.23259111e-14, 1.92051343e-11], [4.30879698e-01, 5.69120302e-01, 9.66619630e-27]])

Числа виглядають дещо схожими на номери нашого класифікатора, але вони дещо відрізняються від кількох останніх відображених цифр. Ми зробили щось не так? Ні. Версія scikit-learn просто використовує інший гіперпараметр var_smoothing=1e-09 . Якщо ми встановимо для цього значення нуль, ми отримуємо саме наші цифри. Ідеально!

Подивіться на регіони рішень нашого класифікатора. Я також позначив три точки, які ми використовували для тестування. Як ви можете бачити з predict_proba виходи. Інші два пункти класифікуються з набагато більшою достовірністю.

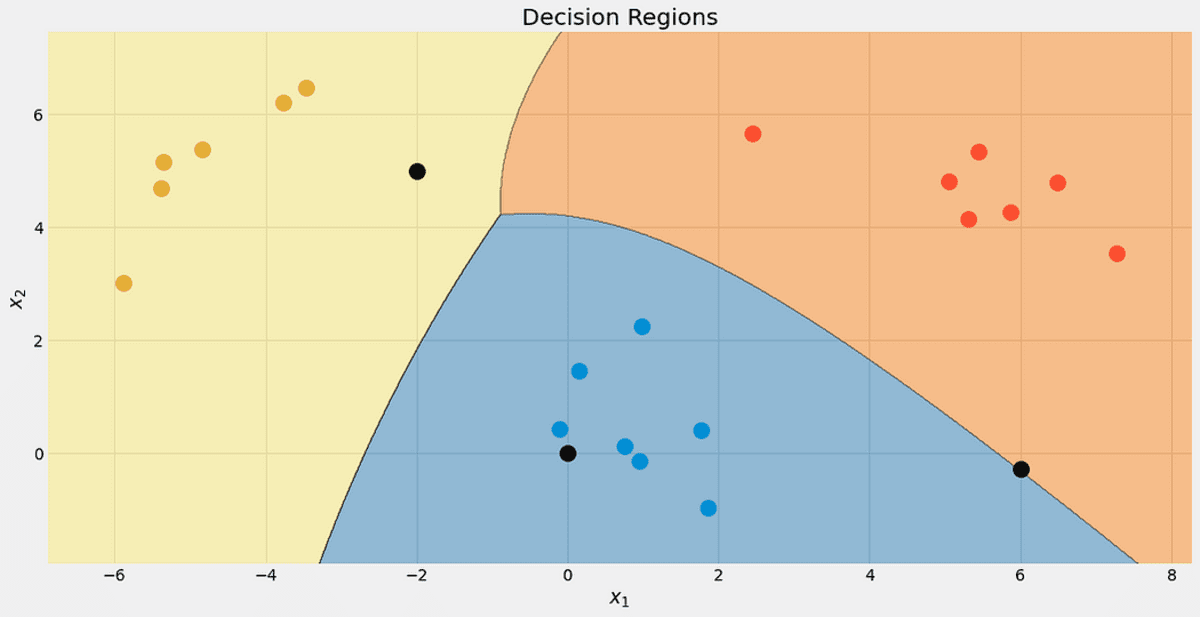
Рішення регіонів з 3 новими пунктами. Зображення автора.

У цій статті ми дізналися, як працює наївний класифікатор Байєса за Гауссом, і дали зрозуміти, чому він розроблений таким чином — це прямий підхід до моделювання ймовірності інтересу. Порівняйте це з логістичною регресією: там імовірність моделюється за допомогою лінійної функції з сигмоподібною функцією, застосованою поверх неї. Це все ще проста модель, але вона не виглядає такою природною, як наївний класифікатор Байєса.

Ми продовжили обчислення кількох прикладів і збирання корисних фрагментів коду. Нарешті, ми реалізували повний гаусівський наївний класифікатор Байєса у спосіб, який добре працює з scikit-learn. Це означає, що ви можете використовувати його, наприклад, у конвеєрах або пошуку в сітці.

Зрештою, ми провели невелику перевірку розумності, імпортувавши власний класифікатор Гаусса Байєса scikit-learn і перевіривши, чи наш і класифікатор scikit-learn дають однаковий результат. Цей тест пройшов успішно.

 
 
Доктор Роберт Кюблер є дослідником даних у Publicis Media та автором Towards Data Science.

 
Оригінал. Повідомлено з дозволу.
 

• Розповсюдження контенту та PR на основі SEO. Отримайте посилення сьогодні.
• Платоблокчейн. Web3 Metaverse Intelligence. Розширені знання. Доступ тут.
• джерело: https://www.kdnuggets.com/2023/03/gaussian-naive-bayes-explained.html?utm_source=rss&utm_medium=rss&utm_campaign=gaussian-naive-bayes-explained