En artificiell intelligensbaserad lösning för Sudoku

Den 29 januari är det nationella pusseldagen, och för att fira det har vi skapat en rolig blogg som beskriver hur man löser Sudoku med artificiell intelligens (AI).

Beskrivning

Innan wordle, den Sudoku pussel var på modet och det är fortfarande väldigt populärt. Under de senaste åren har användningen av optimering metoder för att lösa pusslet har varit ett dominerande tema. Ser "Lösa Sudoku-pussel med optimering i Arkieva".

I nuvarande tider är användningen av AI fokuserad på maskininlärning som omfattar ett brett utbud av metoder från lassoregression till förstärkningsinlärning. Användningen av AI har återuppkom att ta itu med komplex schemaläggning utmaningar. En metod, sökning med backtracking, används ofta och är perfekt för Sudoku.

Den här bloggen kommer att ge en detaljerad beskrivning om hur man använder den här metoden för att lösa Sudoku. Som det visar sig kan "backtracking" hittas i optimerings- och maskininlärningsmotorer och är en hörnsten i den avancerade heuristik som Arkieva använder för schemaläggning. Algoritmen är implementerad i ett "Array Programming Language", ett funktionsorienterat programmeringsspråk som hanterar en rik uppsättning arraystrukturer.

Grunderna i Sudoku

Från Wikipedia: Sudoku är ett logikbaserat, kombinatoriskt nummerplaceringspussel. Målet är att fylla ett 9×9 rutnät med siffror så att varje kolumn, varje rad och vart och ett av de nio 3×3 underrutnät som utgör rutnätet (även kallade "rutor", "block", "regioner", eller "sub-squares") innehåller alla siffror från 1 till 9. Pusselsättaren tillhandahåller ett delvis färdigt rutnät, som vanligtvis har en unik lösning. Gjorda pussel är alltid en typ av latinsk kvadrat med en ytterligare begränsning av innehållet i enskilda regioner. Till exempel får samma enstaka heltal inte förekomma två gånger i samma 9×9-spelbrädrad eller kolumn eller i någon av de nio 3×3-underregionerna på 9×9-spelbrädet.

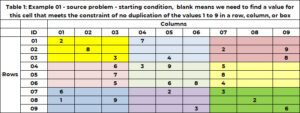
Tabell 1 har ett exempelproblem. Det finns 9 rader och 9 kolumner för totalt 81 celler. Var och en tillåts ha ett och endast ett av nio heltal mellan 1 och 9. I startlösningen har en cell antingen ett enda värde – som fixerar värdet i denna cell till det värdet, eller så är cellen tom, vilket indikerar att vi behöver för att hitta ett värde för den här cellen. Cellen (1,1) har värdet 2 och cell (6,5) har värdet 6. Cell (1,2) och cell (2,3) är tomma, och algoritmen kommer att hitta ett värde för dessa celler.

Komplikationen

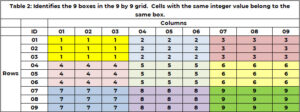
Förutom att tillhöra en och endast en rad och kolumn, tillhör en cell en och endast 1 ruta. Det finns 9 rutor, och de indikeras med färg i Tabell 1. Tabell 2 använder ett unikt heltal mellan 1 och 9 för att identifiera varje ruta eller rutnät. Cellerna med ett radvärde på (1, 2 eller 3) och kolumnvärde på (1, 2 eller 3) tillhör ruta 1. Ruta 6 är radvärden på (4, 5, 6) och kolumnvärden (7, 8) 9). Box-id bestäms av formeln BOX_ID = {3x(floor((ROW_ID-1) /3)} + tak (COL_ID/3). För cellen (5,7), 6 = 3x(floor(5-1) ))/3) + tak (8/3)= 3×1 + 3 = 3+3.

Hjärtat i pusslet

Att hitta ett heltalsvärde mellan 1 och 9 för varje okänd cell så att heltal 1 till 9 används en gång och endast en gång för varje kolumn, varje rad och varje ruta.

Låt oss titta på cell (1,3) som är tom. Rad 1 har redan värdena 2 och 7. Dessa är inte tillåtna i den här cellen. Kolumn 3 har redan värdena 3, 5,6, 7,9. Dessa är inte tillåtna. Ruta 1 (gul) har värdena 2, 3 och 8. Dessa är inte tillåtna. Följande värden är inte tillåtna (2,7); (3, 5, 6, 7, 9); (2, 3, 8). De unika värdena som inte är tillåtna är (2, 3, 5, 6, 7, 8, 9). De enda kandidatvärdena är (1,4).

En lösning skulle vara att tillfälligt tilldela 1 till cell (1,3) och sedan försöka hitta kandidatvärden för en annan cell.

En bakåtspårningslösning: Starta komponenter

Array struktur

Utgångsplatsen är att bestämma en arraystruktur för att lagra källproblemet och stödja sökningen. Tabell 3 har denna arraystruktur. Kolumn 1 är ett unikt heltals-id för varje cell. Värdena sträcker sig från 1 till 81. Kolumn 2 är cellens rad-ID. Kolumn 3 är cellens kolumn-ID. Kolumn 4 är box-id. Kolumn 5 är värdet i cellen. Observera att en cell utan värde får värdet noll istället för blank eller null. Detta håller detta en "endast heltalsuppsättning" - mycket överlägsen för prestanda.

I APL skulle denna array lagras i en 2-dimensionell array där formen är 81 gånger 5. Antag att elementen i Tabell 3 är lagrade i variabeln MAT. Exempel på funktioner är:

Kommandot MAT[1 2 3;] tar tag i de första 3 raderna av MAT
1 1 1 1 2
2 1 2 1 0
3 1 3 1 0
MAT[1 2 3; 4 5] säkrar raderna 1, 2, 3 och bara kolumnerna 4 och 5
1 2
1 0
1 0
(MAT[;5]=0)/MAT[;1] hittar alla celler som behöver ett värde.

INFOGA TABELL 3

Sanity Check: Dubletter

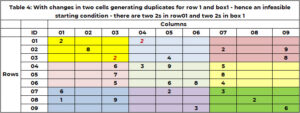
Innan du påbörjar sökningen är det viktigt att kontrollera förståndet! Det är den utgångslösning som är möjlig. Möjligt för Sudoku, om det nu finns dubbletter i valfri rad, kolumn eller ruta. Den nuvarande startlösningen, till exempel, 1 är genomförbar. Tabell 4 har ett exempel där startlösningen har dubbletter. Rad 1 har två värden 2. Område 1 har två värden 2. Funktionen "SANITY_DUPE" hanterar denna logik.

Sanity Check: Alternativ för celler utan värden

En mycket användbar information skulle vara alla möjliga värden för en cell utan ett värde. Om det inte finns några kandidater är detta pussel inte lösbart. En cell kan inte ta på sig ett värde som redan gjort anspråk på av sin granne. Genom att använda tabell 1 för cell (1,3,'1' – den sista 1 är boxiden), dess grannar är rad 1, kolumn 3 och ruta 1. Rad 1 har värdena (2,7); kolumn 3 har värdena (3,5,6,7,9); ruta 1 har värdena (2,3,8). Cell (1,3.1) kan inte ta följande värden (2,3,5,6,7,8,9). De enda alternativen för cell (1,3,1) är (1,4). För cell (4,1,2) används värdena 1, 2, 3, 5, 6, 7, 9 redan i rad 4, kolumn 1 och/eller ruta 4. De enda kandidatvärdena är (4,8) . Unction "SANITY_CAND" hanterar denna logik.

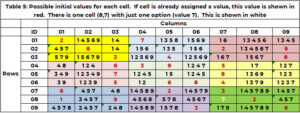
Tabell 5 visar kandidaterna, till exempel 1 i början av sökprocessen. Om en cell redan har tilldelats ett värde i startförhållandena (tabell 1), upprepas detta värde och visas i rött. Om en cell som behöver ett värde bara har ett alternativ visas detta i vitt. Cell (8,7,9) har det enda värdet 7 i vitt. (2,5,8,4,3) görs anspråk på av grannkolumn 7. (1, 2, 9) av rad 8. (3,2,6) av ruta 9. Endast värdet 7 saknas.

Sanity Check: Letar efter konflikter

Informationen som identifierar alla alternativ för celler som behöver ett värde (upplagt i tabell 4), gör det möjligt för oss att identifiera en konflikt innan vi startar sökprocessen. En konflikt uppstår när två celler som behöver ett värde bara har en kandidat, kandidatvärdet är detsamma och de två cellerna är grannar. Från tabell 4 vet vi att den enda cellen som behöver ett värde och bara har en kandidat är cell (8,7,9). Till exempel 1, det finns ingen konflikt.

Vad skulle vara en konflikt? Om det enda möjliga värdet för cell (3,7,3) var 7 (istället för 1, 6, 7), så finns det en konflikt. Cell (8,7) och cell (3,7) är grannar – samma kolumn. Men om det enda möjliga värdet för cell (4,9,2) var 7 (istället för 1, 2, 7) skulle detta inte vara en konflikt. Dessa celler är inte grannar.

Sanity Check Sammanfattning

1. Om det finns dubbletter är startlösningen inte genomförbar.
2. Om en cell som behöver ett värde, inte har några kandidater, så finns det ingen möjlig lösning på detta pussel. Listan med kandidatvärden för varje cell kan användas för att minska sökutrymmet – både för bakåtspårning och optimering.
3. Förmågan att hitta konflikter identifierar att pusslet inte är genomförbart – har ingen lösning – utan en sökprocess. Dessutom identifierar den "problemcellerna".

En bakåtspårningslösning: Sökprocess

Med kärndatastrukturer och hälsokontroll på plats riktar vi vår uppmärksamhet mot sökprocessen. Det återkommande temat är återigen att få datastrukturer på plats för att stödja sökning.

Spåra sökningen

Matrisen Tracker håller reda på gjorda uppdrag

1. Kol 1 är räknaren
2. Kol 2 är antalet tillgängliga alternativ att tilldela den här cellen
   • 1 betyder 1 alternativ tillgängligt, 2 betyder två alternativ osv.
   • 0 betyder – inget alternativ tillgängligt eller återställning till 0 (inget tilldelat värde) och backtracking
3. Kol 3 är cellen som har tilldelats ett värdeindexnummer (1 till 81)
4. Kol 4 är det värde som tilldelats cellen i spårhistoriken
   • Ett värde på 9999 betyder att den här cellen var när återvändsgränden hittades
   • Värdet på ett heltal mellan 1 och 9 inklusive, är det tilldelade värdet till denna cell vid denna tidpunkt i sökprocessen.
   • Ett värde på 0 betyder att den här cellen behöver en tilldelning

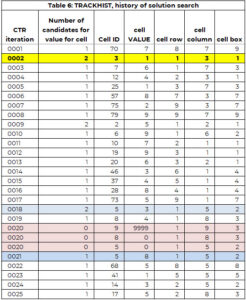
Tracker-arrayen används för att stödja sökprocessen. Arrayen SPÅRHIST har samma struktur som spåraren men behåller historiken för hela sökprocessen. Tabell 6 har en del av TRACKHIST till exempel 1. Det förklaras mer i detalj i ett senare avsnitt.

Dessutom arrayen PAV (en vektor av en vektor), håller reda på tidigare tilldelade värden till denna cell. Detta säkerställer att vi inte återvänder till en misslyckad lösning – liknande det som görs i TABU.

Det finns en valfri loggprocess där sökprocessen skriver ut varje steg.

Startar sökningen

Med bokföring och förnuftskontroll gjorda kan vi nu starta sökprocessen. Stegen är:

1. Finns det några celler kvar som behöver ett värde? – om nej, då är vi klara.
2. För varje cell som behöver ett värde, hitta alla kandidatalternativ för varje cell. Tabell 4 har dessa värden i början av lösningsprocessen. Vid varje iteration uppdateras detta för att tillgodose värden som tilldelats celler.
3. Utvärdera alternativen i denna ordning.
   • Om en cell har NOLL alternativ, sätt sedan tillbaka spårning
   • Hitta alla celler med ett alternativ, välj en av dessa celler, gör den här uppgiften,
     1. och uppdatera spårningstabellen, den aktuella lösningen och PAV.
   • Om alla celler har mer än ett alternativ, välj sedan en cell och ett värde och uppdatera
     1. och uppdatera spårningstabellen, den aktuella lösningen och PAV

Vi kommer att använda tabell 6 som är en del av historien om lösningsprocessen (kallad TRACKHIST) för att illustrera varje steg.

I den första iterationen (CTR=1) väljs cell 70 (rad 8, kol 7, ruta 9) för att tilldelas ett värde. Det finns bara kandidat (7), och detta värde tilldelas cell 70. Dessutom läggs värdet 7 till vektorn för tidigare tilldelade värden (PAV) för cell 70.

I den andra iterationen tilldelas cellen 30 värdet 1. Denna cell hade två kandidatvärden. Det minsta kandidatvärdet tilldelas cellen (bara en godtycklig regel för att göra logiken lätt att följa).

Processen att identifiera en cell som behöver ett värde och tilldela ett värde fungerar bra tills iteration (CTR) 20. Cell 9 behöver värde, men antalet kandidater är NOLL. Det finns två alternativ:

• Det finns ingen lösning på detta pussel.
• Vi ångrar (backtrack) några av uppdragen och tar en annan väg.

Vi letade efter celltilldelningen närmast detta, där det fanns mer än ett alternativ. I det här exemplet inträffade detta vid iteration 18, där cell 5 tilldelas värdet 3, men det fanns två kandidatvärden för cell 5 – värdena 3 och 8.

Mellan cell 5 (CTR = 18) och cell 9 (CTR = 20) tilldelas cell 8 värdet 4 (CTR=19). Vi sätter tillbaka cellerna 8 och 5 på listan "behöver ett värde". Detta fångas i den andra och tredje CTR=20-posten, där värdet är satt till 0. Värdet 3 hålls i PAV-vektorn för cell 5. Det vill säga sökmotorn kan inte tilldela värdet 3 till cell 5.

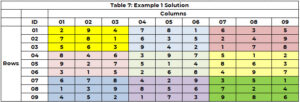
Sökmotorn startar igen för att identifiera ett värde för cell 5 (med 3 inte längre ett alternativ) och tilldelar värdet 8 till cell 5 (CTR=21). Det fortsätter tills alla celler har ett värde eller det finns en cell utan alternativ och det inte finns någon bakåtspårningsväg. Lösningen finns i tabell 7.

Observera, om det finns mer än en kandidat för en cell, är detta en chans för parallell bearbetning.

Jämförelse med MILP Optimization Solution

På ytan är representationen av Sudoku-pusslet dramatiskt annorlunda. AI-metoden använder heltal och är, oavsett mått, en stramare och mer intuitiv representation. Dessutom ger förnuftskontrollerna användbar information för att göra en starkare formulering. MILP-representationen är oändlig binärer (0/1). Binärfilerna är dock kraftfulla representationer med tanke på styrkan hos moderna MILP-lösare.

Internt behåller dock inte MILP-lösaren binärerna utan använder en sparse array-metod för att eliminera lagring av alla nollor. Dessutom dyker algoritmerna för att lösa binärer inte upp förrän på 1980- och 1990-talen. Tidningen 1983 av Crowder, Johnson och Padberg rapporterar om en av de första praktiska lösningarna för optimering med binärer. De noterar vikten av smart förbearbetning och förgrening och bundna metoder som avgörande för en framgångsrik lösning.

Den senaste tidens explosion av användningen av begränsningsprogrammering och programvara som t.ex lokal lösare har tydliggjort vikten av att använda AI-metoder med de ursprungliga optimeringsmetoderna som linjär programmering och minsta kvadrater.

• SEO-drivet innehåll och PR-distribution. Bli förstärkt idag.
• PlatoData.Network Vertical Generative Ai. Styrka dig själv. Tillgång här.
• PlatoAiStream. Web3 Intelligence. Kunskap förstärkt. Tillgång här.
• Platoesg. Kol, CleanTech, Energi, Miljö, Sol, Avfallshantering. Tillgång här.
• PlatoHealth. Biotech och kliniska prövningar Intelligence. Tillgång här.
• Källa: https://blog.arkieva.com/an-artificial-intelligence-based-solution-to-sudoku/?utm_source=rss&utm_medium=rss&utm_campaign=an-artificial-intelligence-based-solution-to-sudoku