Vitalik Buterin via Vitalik Buterin-bloggen
Dette er et speil av innlegget kl https://medium.com/@VitalikButerin/quadratic-aritmetic-programs-from-zero-to-hero-f6d558cea649
Det har vært stor interesse i det siste for teknologien bak zk-SNARKs, og det blir stadig flere folk prøver å avmystifisere noe som mange har kommet til å kalle "månematematikk" på grunn av dens oppfattede rene og ufattelige kompleksitet. zk-SNARK-er er faktisk ganske utfordrende å forstå, spesielt på grunn av det store antallet bevegelige deler som må komme sammen for at det hele skal fungere, men hvis vi bryter ned teknologien bit for bit, blir det enklere å forstå det.
Hensikten med dette innlegget er ikke å tjene som en fullstendig introduksjon til zk-SNARKs; det forutsetter som bakgrunnskunnskap at (i) du vet hva zk-SNARK er og hva de gjør, og (ii) kan nok matematikk til å kunne resonnere om ting som polynomer (hvis utsagnet �(�)+�(�) =(�+�)(�) , der � og � er polynomer, virker naturlig og åpenbart for deg, da er du på rett nivå). Snarere graver innlegget dypere inn i maskineriet bak teknologien, og prøver å forklare så godt som mulig den første halvdelen av rørledningen, som tegnet av zk-SNARK-forsker Eran Tromer her:

Trinnene her kan deles opp i to halvdeler. For det første kan ikke zk-SNARK-er brukes direkte på noe beregningsproblem; snarere må du konvertere problemet til riktig "form" for at problemet skal kunne opereres. Skjemaet kalles et "kvadratisk aritmetisk program" (QAP), og å transformere koden til en funksjon til en av disse er i seg selv svært ikke-trivielt. Sammen med prosessen for å konvertere koden til en funksjon til en QAP er en annen prosess som kan kjøres ved siden av, slik at hvis du har en input til koden, kan du lage en tilsvarende løsning (noen ganger kalt "vitne" til QAP). Etter dette er det en annen ganske intrikat prosess for å lage det faktiske "null kunnskapsbeviset" for dette vitnet, og en egen prosess for å verifisere et bevis på at noen andre gir deg videre, men dette er detaljer som er utenfor rammen for dette innlegget .
Eksemplet vi skal velge er enkelt: å bevise at du kjenner løsningen på en kubikkligning: �3+�+5=35 (hint: svaret er 3). Dette problemet er enkelt nok til at den resulterende QAP ikke vil være så stor at den er skremmende, men ikke-triviell nok til at du kan se alle maskineriet spille inn.
La oss skrive ut funksjonen vår som følger:
def qeval(x):
y = x**3
return x + y + 5Det enkle programmeringsspråket med spesialformål som vi bruker her støtter grunnleggende aritmetikk (+, −, ⋅, /), eksponentiering med konstant effekt (�7 men ikke ��) og variabeltilordning, som er kraftig nok til at du teoretisk kan gjøre enhver beregning inne i den (så lenge antallet beregningstrinn er begrenset; ingen løkker tillatt). Merk at modulo (%) og sammenligningsoperatorer (<, >, ≤, ≥) IKKE støttes, siden det ikke er noen effektiv måte å gjøre modulo eller sammenligning direkte i finitt syklisk gruppe-aritmetikk (vær takknemlig for dette; hvis det fantes en måte) for å gjøre begge deler, vil elliptisk kurvekryptografi bli brutt raskere enn du kan si "binært søk" og "kinesisk restsetning").
Du kan utvide språket til modulo og sammenligninger ved å gi bitdekomponeringer (f.eks. 13=23+22+1) som hjelpeinnganger, bevise riktigheten av disse dekomponeringene og gjøre regnestykket i binære kretser; i finite field aritmetikk er det også mulig å utføre likhetskontroller (==) og faktisk litt enklere, men disse er begge detaljer vi ikke kommer inn på akkurat nå. Vi kan utvide språket til å støtte betingelser (f.eks. hvis �<5:�=7; annet: �=9) ved å konvertere dem til en aritmetisk form: �=7⋅(�<5)+9⋅(�≥5) ) Vær imidlertid oppmerksom på at begge "banene" til den betingede må kjøres, og hvis du har mange nestede betingelser, kan dette føre til en stor mengde overhead.
La oss nå gå gjennom denne prosessen trinn for trinn. Hvis du vil gjøre dette selv for en kodebit, kan jeg implementert en kompilator her (kun for pedagogiske formål; ikke klar for å lage QAP-er for virkelige zk-SNARK-er ennå!).
utflating
Det første trinnet er en "utflatnings"-prosedyre, hvor vi konverterer den opprinnelige koden, som kan inneholde vilkårlig komplekse utsagn og uttrykk, til en sekvens av utsagn som har to former: �=� (hvor � kan være en variabel eller et tall ) og �=� (��) � (hvor �� kan være +, −, ⋅, / og � og � kan være variabler, tall eller seg selv underuttrykk). Du kan tenke på hver av disse utsagnene som på en måte som logiske porter i en krets. Resultatet av utflatningsprosessen for koden ovenfor er som følger:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5Leser du originalkoden og koden her, kan du ganske enkelt se at de to er likeverdige.
Porter til R1CS
Nå konverterer vi dette til noe som kalles et rang-1 begrensningssystem (R1CS). En R1CS er en sekvens av grupper av tre vektorer (�, �, �), og løsningen til en R1CS er en vektor �, der � må tilfredsstille ligningen �.�⋅�.�−�.�=0, der . representerer punktproduktet – i enklere termer, hvis vi "zipper sammen" � og �, multipliserer de to verdiene i samme posisjon, og deretter tar summen av disse produktene, gjør deretter det samme med � og � og deretter � og � , så er det tredje resultatet lik produktet av de to første resultatene. For eksempel er dette en fornøyd R1CS:
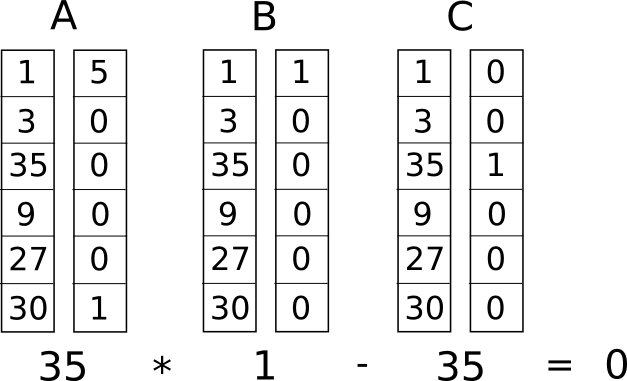
Men i stedet for å ha bare én begrensning, kommer vi til å ha mange begrensninger: én for hver logisk port. Det er en standard måte å konvertere en logisk port til en (�,�,�) trippel avhengig av hva operasjonen er (+, −, ⋅ eller /) og om argumentene er variabler eller tall. Lengden på hver vektor er lik det totale antallet variabler i systemet, inkludert en dummyvariabel ~en ved den første indeksen som representerer tallet 1, inngangsvariablene, en dummyvariabel ~out som representerer utdataene, og deretter alle mellomliggende variabler (���1 og ���2 ovenfor); vektorene vil generelt være svært sparsomme, bare fylle ut sporene som tilsvarer variablene som påvirkes av en bestemt logisk port.
Først gir vi variabeltilordningen som vi skal bruke:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'Løsningsvektoren vil bestå av tilordninger for alle disse variablene, i den rekkefølgen.
Nå gir vi (�,�,�) trippelen for den første porten:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Du kan se at hvis løsningsvektoren inneholder 3 i den andre posisjonen og 9 i den fjerde posisjonen, vil prikkproduktsjekken, uavhengig av resten av innholdet i løsningsvektoren, koke ned til 3⋅3=9, og så det går over. Hvis løsningsvektoren har −3 i den andre posisjonen og 9 i den fjerde posisjonen, vil kontrollen også bestå; faktisk, hvis løsningsvektoren har 7 i den andre posisjonen og 49 i den fjerde posisjonen, vil den kontrollen fortsatt passere - hensikten med denne første kontrollen er kun å verifisere konsistensen av inngangene og utgangene til den første porten.
La oss nå gå videre til den andre porten:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]I en lignende stil som den første punktproduktsjekken, her sjekker vi at ���1⋅�=�.
Nå, den tredje porten:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]Her er mønsteret noe annerledes: det er å multiplisere det første elementet i løsningsvektoren med det andre elementet, deretter med det femte elementet, legge til de to resultatene og sjekke om summen er lik det sjette elementet. Fordi det første elementet i løsningsvektoren alltid er ett, er dette bare en addisjonssjekk som sjekker at utgangen er lik summen av de to inngangene.
Til slutt, den fjerde porten:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]Her evaluerer vi den siste sjekken, ~out =���2+5. Punktproduktkontrollen fungerer ved å ta det sjette elementet i løsningsvektoren, legge til fem ganger det første elementet (påminnelse: det første elementet er 1, så dette betyr i praksis å legge til 5), og sjekke det mot det tredje elementet, som er der vi lagre utdatavariabelen.
Og der har vi vår R1CS med fire begrensninger. Vitnet er ganske enkelt tilordningen til alle variablene, inkludert input, output og interne variabler:
[1, 3, 35, 9, 27, 30]Du kan beregne dette selv ved ganske enkelt å "utføre" den flate koden ovenfor, starte med tildelingen av inngangsvariabelen �=3, og sette inn verdiene til alle mellomvariablene og utdataene mens du beregner dem.
Den komplette R1CS satt sammen er:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]R1CS til QAP
Det neste trinnet er å ta denne R1CS og konvertere den til QAP-form, som implementerer nøyaktig samme logikk bortsett fra å bruke polynomer i stedet for punktprodukter. Vi gjør dette som følger. Vi går 3fra fire grupper på tre vektorer med lengde seks til seks grupper på tre grader-3 polynomer, der vi evaluerer polynomene ved hver x koordinat representerer en av begrensningene. Det vil si at hvis vi evaluerer polynomene ved �=1, får vi vårt første sett med vektorer, hvis vi evaluerer polynomene ved �=2, får vi vårt andre sett med vektorer, og så videre.
Vi kan gjøre denne transformasjonen ved å bruke noe som kalles a Lagrange-interpolasjon. Problemet som en Lagrange-interpolasjon løser er dette: hvis du har et sett med punkter (dvs. (�,�) koordinatpar), så gir en Lagrange-interpolasjon på disse punktene deg et polynom som går gjennom alle disse punktene. Vi gjør dette ved å dekomponere problemet: for hver koordinat lager vi et polynom som har ønsket koordinat ved den koordinaten og en koordinat på 0 på alle de andre koordinatene vi er interessert i, og deretter for å få den endelige resultat legger vi alle polynomene sammen.
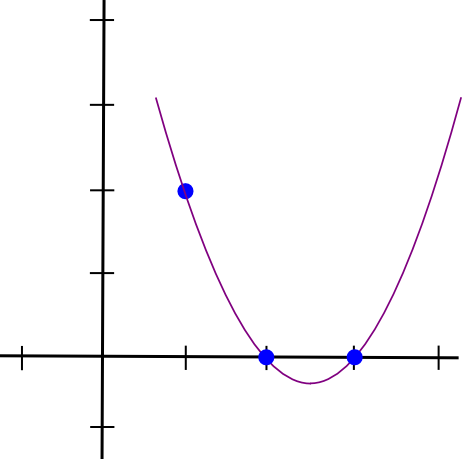
La oss ta et eksempel. Anta at vi ønsker et polynom som går gjennom (1,3),(2,2) og (3,4). Vi starter med å lage et polynom som går gjennom (1,3),(2,0) og (3,0). Som det viser seg, er det enkelt å lage et polynom som "stikker ut" ved �=1 og er null på de andre interessepunktene; vi gjør ganske enkelt:
(x - 2) * (x - 3)Som ser slik ut:
Nå trenger vi bare å "skalere" den slik at høyden ved x=1 er riktig:
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))Dette gir oss:
1.5 * x**2 - 7.5 * x + 9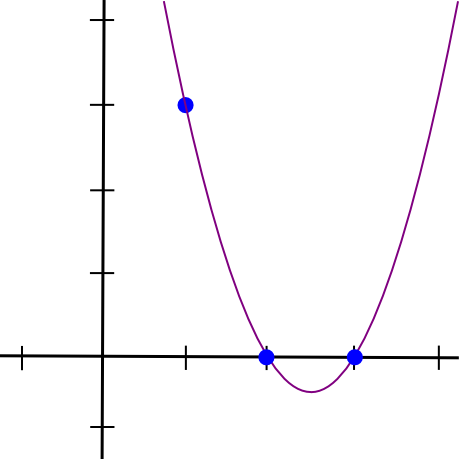
Vi gjør det samme med de to andre punktene, og får to andre polynomer som ligner på hverandre, bortsett fra at de "stikker ut" ved �=2 og �=3 i stedet for �=1. Vi legger alle tre sammen og får:
1.5 * x**2 - 5.5 * x + 7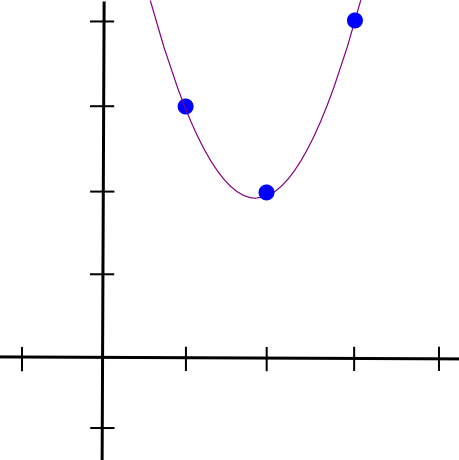
Med akkurat de koordinatene vi ønsker. Algoritmen som beskrevet ovenfor tar �(�3) tid, siden det er � punkter og hvert punkt krever �(�2) tid for å multiplisere polynomene sammen; med litt tenkning kan dette reduseres til �(�2) tid, og med mye mer tenkning, ved å bruke raske Fourier-transformasjonsalgoritmer og lignende, kan det reduseres ytterligere – en avgjørende optimalisering når funksjoner som blir brukt i zk -SNARK har i praksis ofte mange tusen porter.
La oss nå bruke Lagrange-interpolasjon til å transformere R1CS. Det vi skal gjøre er å ta den første verdien ut av hver � vektor, bruke Lagrange-interpolasjon for å lage et polynom av det (hvor å evaluere polynomet ved � får du den første verdien av den �th � vektoren), gjenta prosessen for den første verdien av hver � og � vektor, og gjenta deretter den prosessen for de andre verdiene, den tredje verdiene, og så videre. For enkelhets skyld gir jeg svarene akkurat nå:
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]Koeffisientene er i stigende rekkefølge, så det første polynomet over er faktisk 0.833⋅�3—5⋅�2+9.166⋅�−5. Dette settet med polynomer (pluss et Z-polynom som jeg vil forklare senere) utgjør parametrene for denne spesielle QAP-forekomsten. Merk at alt arbeidet frem til dette punktet bare må gjøres én gang for hver funksjon du prøver å bruke zk-SNARKs for å verifisere; når QAP-parametrene er generert, kan de brukes på nytt.
La oss prøve å evaluere alle disse polynomene ved �=1. Å evaluere et polynom ved �=1 betyr ganske enkelt å legge sammen alle koeffisientene (som 1�=1 for alle �), så det er ikke vanskelig. Vi får:
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0Og se, det vi har her er nøyaktig det samme som settet med tre vektorer for den første logiske porten som vi laget ovenfor.
Sjekker QAP
Hva er vitsen med denne vanvittige transformasjonen? Svaret er at i stedet for å sjekke begrensningene i R1CS individuelt, kan vi nå sjekke alle begrensningene på samme tid ved å gjøre punktproduktsjekken på polynomene.
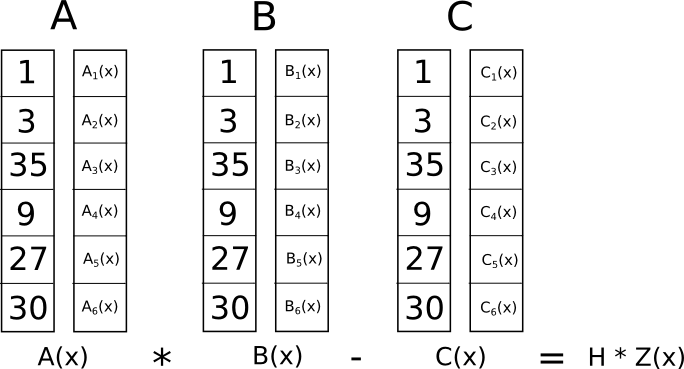
Fordi punktproduktsjekken i dette tilfellet er en serie addisjoner og multiplikasjoner av polynomer, vil resultatet i seg selv være et polynom. Hvis det resulterende polynomet, evaluert ved hver � koordinat som vi brukte ovenfor for å representere en logisk port, er lik null, betyr det at alle sjekkene består; hvis det resulterende polynomet evaluert ved minst én av �-koordinatene som representerer en logisk port gir en verdi som ikke er null, betyr det at verdiene som går inn og ut av den logiske porten er inkonsistente (dvs. porten er �=�⋅�� �1 men de oppgitte verdiene kan være �=2,���1=2 og �=5).
Merk at det resulterende polynomet ikke i seg selv trenger å være null, og i de fleste tilfeller vil det faktisk ikke være det; den kan ha hvilken som helst oppførsel på punktene som ikke samsvarer med noen logiske porter, så lenge resultatet er null på alle punktene som do tilsvarer en eller annen port. For å kontrollere riktigheten, evaluerer vi faktisk ikke polynomet �=�.�⋅�.�−�.� ved hvert punkt som tilsvarer en port; i stedet deler vi � med et annet polynom, �, og kontrollerer at � jevnt deler � – det vil si at divisjonen �/� ikke etterlater noen rest.
� er definert som (�−1)⋅(�−2)⋅(�−3)... – det enkleste polynomet som er lik null i alle punkter som tilsvarer logiske porter. Det er et elementært faktum i algebra at noen polynom som er lik null på alle disse punktene må være et multiplum av dette minimale polynomet, og hvis et polynom er et multiplum av � vil evalueringen ved et av disse punktene være null; denne ekvivalensen gjør jobben vår mye enklere.
Nå, la oss faktisk gjøre prikkproduktsjekken med polynomene ovenfor. Først de mellomliggende polynomene:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]Nå, �.�⋅�.�—�.�:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Nå, det minimale polynomet �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):
Z = [24, -50, 35, -10, 1]Og hvis vi deler resultatet ovenfor med �, får vi:
h = t / Z = [-3.666, 17.055, -3.444]Uten rest.
Og så har vi løsningen for QAP. Hvis vi prøver å forfalske noen av variablene i R1CS-løsningen som vi utleder denne QAP-løsningen fra - for eksempel sett den siste til 31 i stedet for 30, så får vi et � polynom som mislykkes i en av kontrollene (i det spesielle tilfelle, vil resultatet ved �=3 være lik −1 i stedet for 0), og dessuten � vil ikke være et multiplum av �; snarere, å dele �/� ville gi en rest på [−5.0,8.833,−4.5,0.666].
Merk at ovenstående er en forenkling; «i den virkelige verden» vil addisjon, multiplikasjon, subtraksjon og divisjon ikke skje med regulære tall, men heller med endelige feltelementer - en skummel form for aritmetikk som er selvkonsistent, så alle de algebraiske lovene vi kjenner og elsker fortsatt stemmer, men der alle svar er elementer i et sett med begrenset størrelse, vanligvis heltall innenfor området fra 0 til �−1 for noen �. For eksempel, hvis �=13, så 1/2=7 (og 7⋅2=1),3⋅5=2, og så videre. Ved å bruke finite field aritmetikk fjerner du behovet for å bekymre deg for avrundingsfeil og lar systemet fungere fint med elliptiske kurver, som ender opp med å være nødvendig for resten av zk-SNARK-maskineriet som gjør zk-SNARK-protokollen faktisk sikker.
Spesiell takk til Eran Tromer for å hjelpe meg med å forklare mange detaljer om den indre funksjonen til zk-SNARKs for meg.
- SEO-drevet innhold og PR-distribusjon. Bli forsterket i dag.
- PlatoData.Network Vertical Generative Ai. Styrk deg selv. Tilgang her.
- PlatoAiStream. Web3 Intelligence. Kunnskap forsterket. Tilgang her.
- PlatoESG. Karbon, CleanTech, Energi, Miljø, Solenergi, Avfallshåndtering. Tilgang her.
- PlatoHelse. Bioteknologisk og klinisk etterretning. Tilgang her.
- BlockOffsets. Modernisering av eierskap for miljøkompensasjon. Tilgang her.
- kilde: Platon Data Intelligence.
