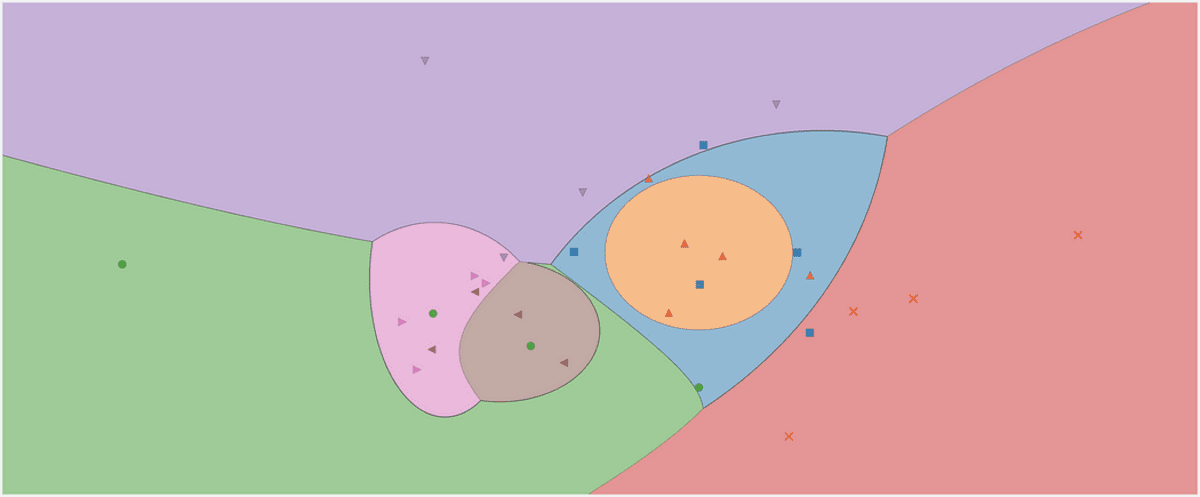
Gaussisk naiv Bayes, forklart

Publisert av Platon

Følgere: 0

Gaussisk naiv Bayes, forklart
Beslutningsregionen til en gaussisk naiv Bayes-klassifiser. Bilde av forfatteren.

Jeg tror dette er en klassiker i begynnelsen av hver datavitenskapskarriere: den Naiv Bayes-klassifisering. Eller jeg burde heller si det familie av naive Bayes-klassifiserere, da de kommer i mange smaker. For eksempel er det en multinomial naiv Bayes, en Bernoulli-naiv Bayes, og også en gaussisk naiv Bayes-klassifiser, hver forskjellige i bare en liten detalj, som vi vil finne ut. De naive Bayes-algoritmene er ganske enkle i design, men viste seg å være nyttige i mange komplekse situasjoner i den virkelige verden.

I denne artikkelen kan du lære

hvordan de naive Bayes-klassifikatorene fungerer,
hvorfor det er fornuftig å definere dem slik de er og
hvordan implementere dem i Python ved hjelp av NumPy.

Du finner koden på min Github.

Det kan hjelpe litt å sjekke ut min primer om Bayesiansk statistikk En mild introduksjon til Bayesian Inference å venne seg til Bayes-formelen. Siden vi skal implementere klassifisereren på en scikit-læringskonform måte, er det også verdt å sjekke ut artikkelen min Bygg din egen tilpassede scikit-learn-regresjon. Imidlertid er scikit-learn-overheaden ganske liten, og du bør uansett kunne følge med.

Vi vil begynne å utforske den forbløffende enkle teorien om naiv Bayes-klassifisering og deretter gå til implementeringen.

Hva er vi egentlig interessert i når vi klassifiserer? Hva gjør vi egentlig, hva er input og output? Svaret er enkelt:

Gitt et datapunkt x, hva er sannsynligheten for at x tilhører en klasse c?

Det er alt vi ønsker å svare med noen klassifisering. Du kan modellere dette utsagnet direkte som en betinget sannsynlighet: p(c|x).

For eksempel hvis det er

3 klasser c₁, c₂, cXNUMXog
x består av 2 funksjoner x₁, x₂,

resultatet av en klassifisering kan være noe sånt som p(c₁|x₁, x₂)=0.3, p(c₂|x₁, x₂)=0.5 og p(cXNUMX|x₁, x₂)=0.2. Hvis vi bryr oss om en enkelt etikett som utgang, ville vi valgt den med høyest sannsynlighet, dvs c₂ med en sannsynlighet på 50 % her.

Den naive Bayes-klassifisereren prøver å beregne disse sannsynlighetene direkte.

Naiv Bayes

Ok, så gitt et datapunkt x, vi ønsker å beregne p(c|x) for alle klasser c og deretter sende ut c med størst sannsynlighet. I formler ser du ofte dette som

Gaussisk naiv Bayes, forklart
Bilde av forfatteren.

OBS: max p(c|x) returnerer maksimal sannsynlighet mens argmax p(c|x) returnerer c med denne høyeste sannsynligheten.

Men før vi kan optimalisere p(c|x), må vi kunne beregne det. Til dette bruker vi Bayes 'teorem:

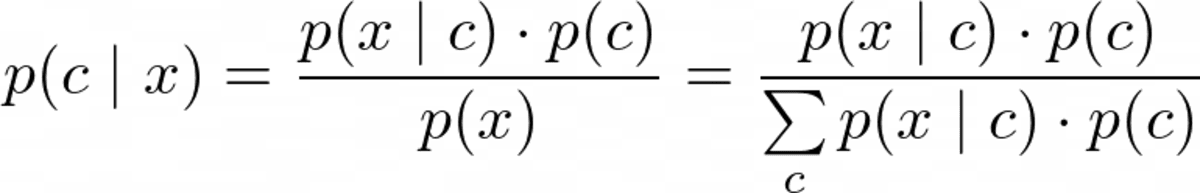
Gaussisk naiv Bayes, forklart
Bayes teorem. Bilde av forfatteren.

Dette er Bayes-delen av naive Bayes. Men nå har vi følgende problem: Hva er p(x|c) Og p(c)?

Dette er hva treningen til en naiv Bayes-klassifiserer handler om.

Treningen

For å illustrere alt, la oss bruke et leketøysdatasett med to virkelige funksjoner x₁, x₂og tre klasser c₁, c₂, cXNUMX i følgende.

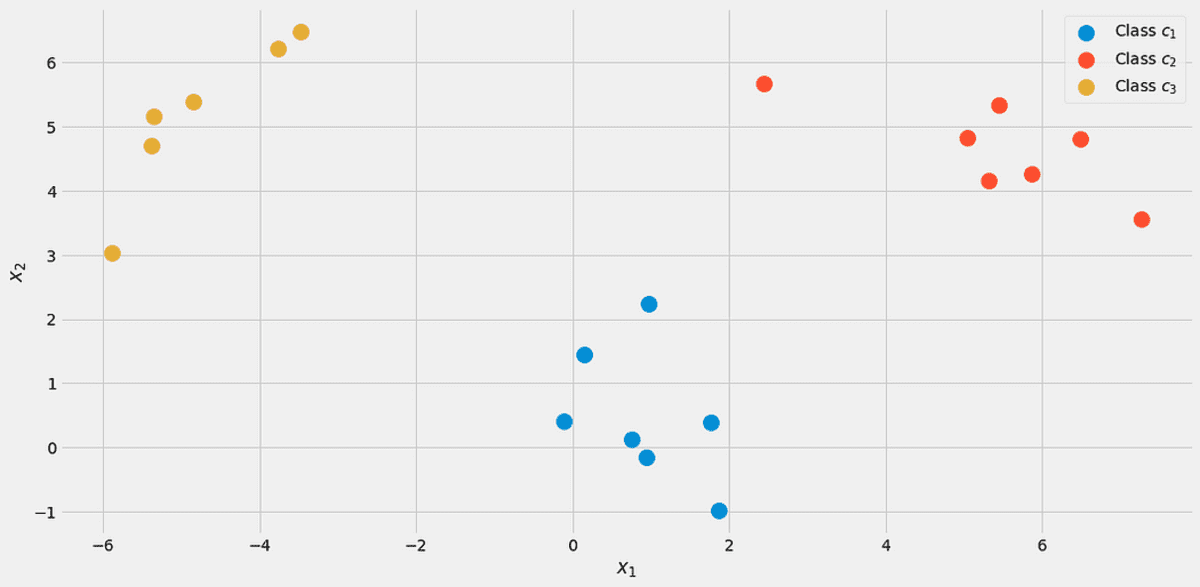
Gaussisk naiv Bayes, forklart
Dataene, visualisert. Bilde av forfatteren.

Du kan opprette dette eksakte datasettet via

from sklearn.datasets import make_blobs X, y = make_blobs(n_samples=20, centers=[(0,0), (5,5), (-5, 5)], random_state=0)

La oss starte med klasse sannsynlighet p(c), sannsynligheten for at noen klasse c er observert i det merkede datasettet. Den enkleste måten å estimere dette på er å bare beregne de relative frekvensene til klassene og bruke dem som sannsynlighetene. Vi kan bruke datasettet vårt til å se hva dette betyr nøyaktig.

Det er 7 av 20 poeng merket klasse c₁ (blå) i datasettet, derfor sier vi p(c₁)=7/20. Vi har 7 poeng for klasse c₂ (rød) også, derfor setter vi p(c₂)=7/20. Den siste timen cXNUMX (gul) har bare 6 poeng, derav p(cXNUMX)=6/20.

Denne enkle beregningen av klassesannsynlighetene ligner en maksimal sannsynlighetstilnærming. Du kan imidlertid også bruke en annen i forkant distribusjon, hvis du vil. For eksempel, hvis du vet at dette datasettet ikke er representativt for den sanne populasjonen fordi klassen cXNUMX skal vises i 50 % av tilfellene, så setter du p(c₁)=0.25, p(c₂)=0.25 og p(cXNUMX)=0.5. Uansett hva som hjelper deg med å forbedre ytelsen på testsettet.

Vi henvender oss nå til sannsynligheten p(x|c)=p(x₁, x₂|c). En tilnærming for å beregne denne sannsynligheten er å filtrere datasettet for prøver med etikett c og prøv så å finne en fordeling (f.eks. en 2-dimensjonal Gaussian) som fanger opp trekkene x₁, x₂.

Dessverre har vi vanligvis ikke nok prøver per klasse til å gjøre en riktig estimering av sannsynligheten.

For å kunne bygge en mer robust modell, lager vi naiv antagelse at funksjonene x₁, x₂ er stokastisk uavhengiggitt c. Dette er bare en fancy måte å gjøre regnestykket enklere via

Gaussisk naiv Bayes, forklart
Bilde av forfatteren

for hver klasse c. Det er her naive del av naive Bayes kommer fra fordi denne ligningen ikke holder generelt. Likevel, selv da gir den naive Bayes gode, noen ganger fremragende resultater i praksis. Spesielt for NLP-problemer med bag-of-word-funksjoner, skinner den multinomiale naive Bayes.

Hvis funksjonene dine bare er 0 og 1, kan du bruke en Bernoulli distribusjon. Hvis de er heltall, a Multinomial fordeling. Vi har imidlertid reelle funksjonsverdier og bestemmer oss for en Gaussian distribusjon, derav navnet Gaussisk naive Bayes. Vi antar følgende form

Gaussisk naiv Bayes, forklart
Bilde av forfatteren.

hvor μᵢ,ⱼ er gjennomsnittet og σᵢ,ⱼ er standardavviket som vi må estimere fra dataene. Dette betyr at vi får ett gjennomsnitt for hver funksjon i sammen med en klasse cⱼ, i vårt tilfelle betyr 2*3=6. Det samme gjelder standardavvikene. Dette krever et eksempel.

La oss prøve å anslå μ₂,₁ og σ₂,₁. Fordi j=1, vi er kun interessert i klassen c₁, la oss bare beholde prøver med denne etiketten. Følgende prøver gjenstår:

# samples with label = c_1 array([[ 0.14404357, 1.45427351], [ 0.97873798, 2.2408932 ], [ 1.86755799, -0.97727788], [ 1.76405235, 0.40015721], [ 0.76103773, 0.12167502], [-0.10321885, 0.4105985 ], [ 0.95008842, -0.15135721]])

Nå på grunn av i=2 vi må bare vurdere den andre kolonnen. μ₂,₁ er gjennomsnittet og σ₂,₁ standardavviket for denne kolonnen, dvs μ₂, 0.49985176 = XNUMX og σ₂, 0.9789976 = XNUMX.

Disse tallene gir mening hvis du ser på spredningsplottet ovenfra igjen. Funksjonene x₂ av prøvene fra klassen c₁ er rundt 0.5, som du kan se av bildet.

Vi beregner dette nå for de andre fem kombinasjonene, og vi er ferdige!

I Python kan du gjøre det slik:

from sklearn.datasets import make_blobs
import numpy as np # Create the data. The classes are c_1=0, c_2=1 and c_3=2.
X, y = make_blobs( n_samples=20, centers=[(0, 0), (5, 5), (-5, 5)], random_state=0
) # The class probabilities.
# np.bincounts counts the occurence of each label.
prior = np.bincount(y) / len(y) # np.where(y==i) returns all indices where the y==i.
# This is the filtering step.
means = np.array([X[np.where(y == i)].mean(axis=0) for i in range(3)])
stds = np.array([X[np.where(y == i)].std(axis=0) for i in range(3)])

Vi mottar

# priors
array([0.35, 0.35, 0.3 ])
# means array([[ 0.90889988, 0.49985176], [ 5.4111385 , 4.6491892 ], [-4.7841679 , 5.15385848]])
# stds
array([[0.6853714 , 0.9789976 ], [1.40218915, 0.67078568], [0.88192625, 1.12879666]])

Dette er resultatet av opplæringen av en gaussisk naiv Bayes-klassifiser.

Gjøre spådommer

Den komplette prediksjonsformelen er

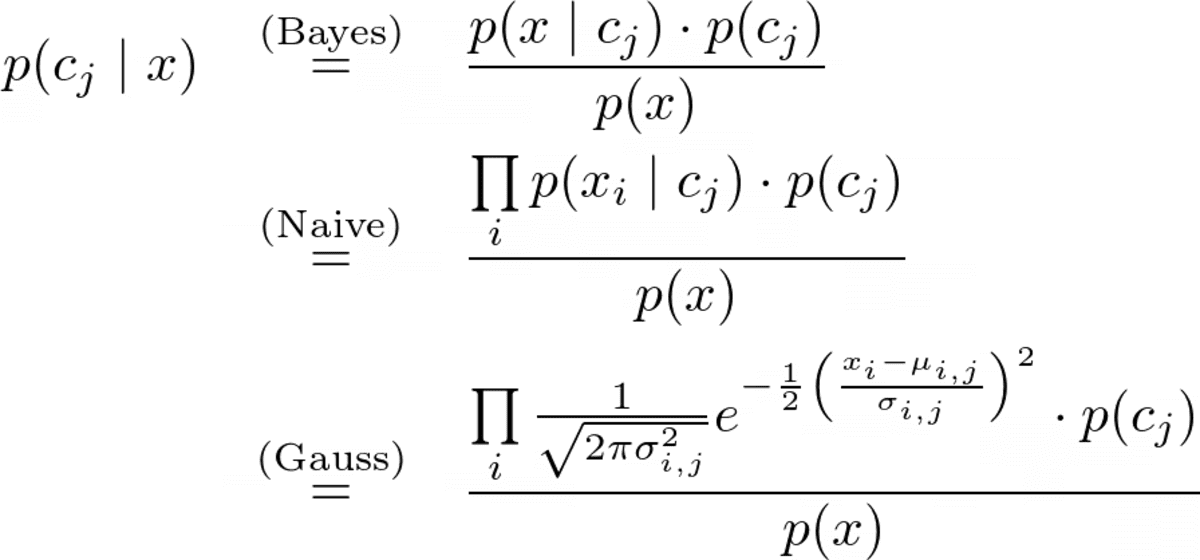
Gaussisk naiv Bayes, forklart
Bilde av forfatteren.

La oss anta et nytt datapunkt x*=(-2, 5) kommer inn.

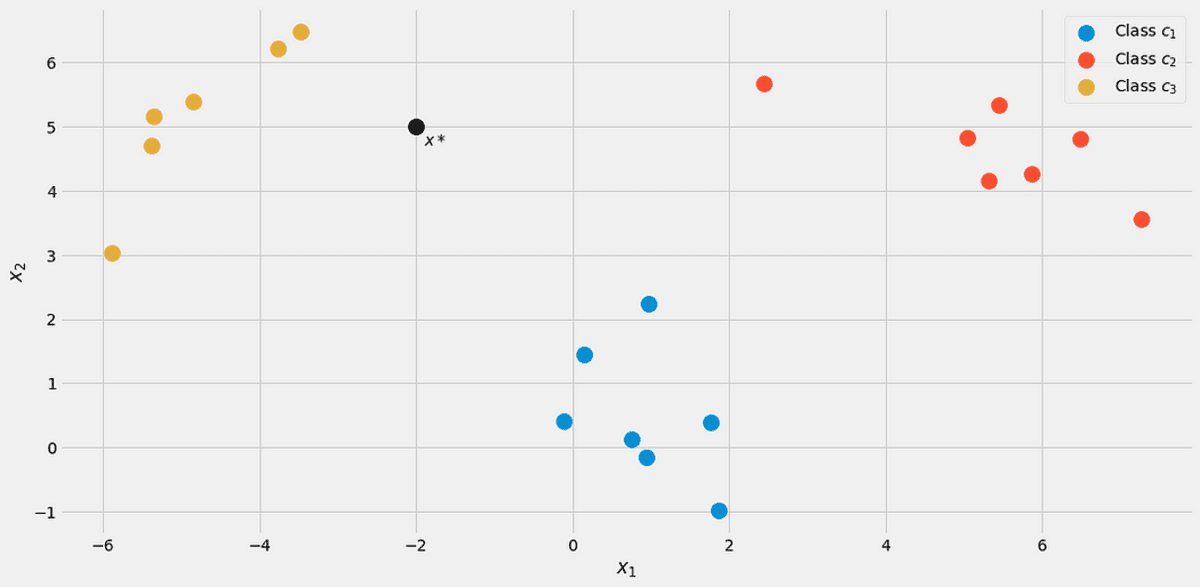
Gaussisk naiv Bayes, forklart
Bilde av forfatteren.

For å se hvilken klasse den tilhører, la oss beregne p(c|x*) for alle klasser. Fra bildet skal det tilhøre klassen cXNUMX = 2, men la oss se. La oss ignorere nevneren p(x) For ett øyeblikk. Ved å bruke følgende sløyfe beregnes nominatorene for j = 1, 2, 3.

x_new = np.array([-2, 5]) for j in range(3): print( f"Probability for class {j}: {(1/np.sqrt(2*np.pi*stds[j]**2)*np.exp(-0.5*((x_new-means[j])/stds[j])**2)).prod()*p[j]:.12f}" )

Vi mottar

Probability for class 0: 0.000000000263
Probability for class 1: 0.000000044359
Probability for class 2: 0.000325643718

Selvfølgelig disse sannsynligheter (vi bør ikke kalle dem slik) ikke legg sammen til én siden vi ignorerte nevneren. Dette er imidlertid ikke noe problem siden vi bare kan ta disse unormaliserte sannsynlighetene og dele dem på summen, så vil de summere seg til én. Så, ved å dele disse tre verdiene med summen av omtrent 0.00032569, får vi

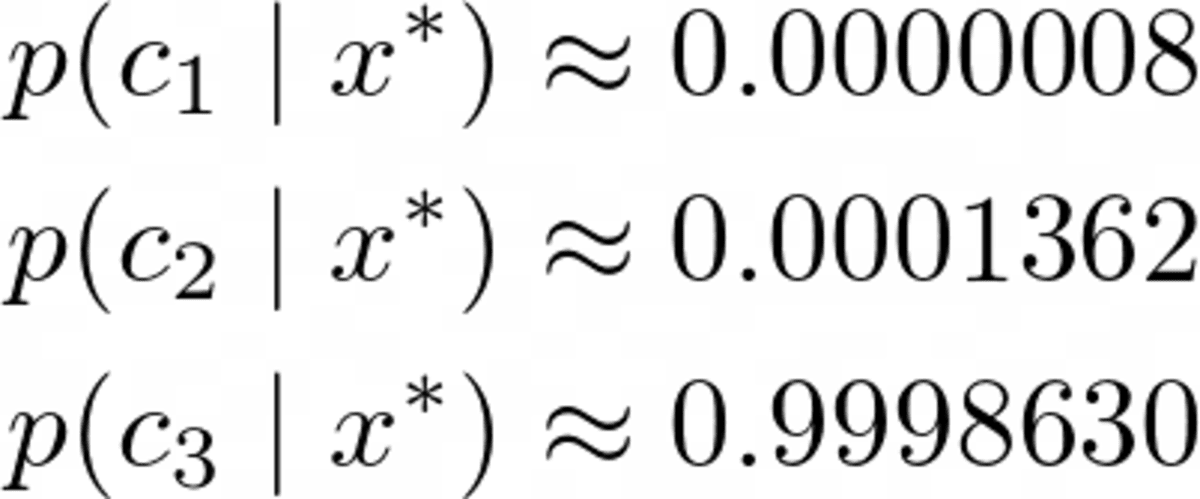
Gaussisk naiv Bayes, forklart
Bilde av forfatteren.

En klar vinner, som vi forventet. Nå, la oss implementere det!

Denne implementeringen er langt på vei ikke effektiv, ikke numerisk stabil, den tjener bare et pedagogisk formål. Vi har diskutert det meste, så det skal være lett å følge med nå. Du kan ignorere alle check funksjoner, eller les artikkelen min Bygg din egen tilpassede scikit-learn hvis du er interessert i hva de nøyaktig gjør.

Bare merk at jeg implementerte en predict_proba metoden først for å beregne sannsynligheter. Metoden predict bare kaller denne metoden og returnerer indeksen (=klasse) med høyest sannsynlighet ved å bruke en argmax-funksjon (der er den igjen!). Klassen venter på klasser fra 0 til k-1, hvor k er antall klasser.

import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted class GaussianNaiveBayesClassifier(BaseEstimator, ClassifierMixin): def fit(self, X, y): X, y = check_X_y(X, y) self.priors_ = np.bincount(y) / len(y) self.n_classes_ = np.max(y) + 1 self.means_ = np.array( [X[np.where(y == i)].mean(axis=0) for i in range(self.n_classes_)] ) self.stds_ = np.array( [X[np.where(y == i)].std(axis=0) for i in range(self.n_classes_)] ) return self def predict_proba(self, X): check_is_fitted(self) X = check_array(X) res = [] for i in range(len(X)): probas = [] for j in range(self.n_classes_): probas.append( ( 1 / np.sqrt(2 * np.pi * self.stds_[j] ** 2) * np.exp(-0.5 * ((X[i] - self.means_[j]) / self.stds_[j]) ** 2) ).prod() * self.priors_[j] ) probas = np.array(probas) res.append(probas / probas.sum()) return np.array(res) def predict(self, X): check_is_fitted(self) X = check_array(X) res = self.predict_proba(X) return res.argmax(axis=1)

Testing av implementeringen

Selv om koden er ganske kort, er den fortsatt for lang til å være helt sikker på at vi ikke har gjort noen feil. Så la oss sjekke hvordan det går mot scikit-learn GaussianNB klassifiserer.

my_gauss = GaussianNaiveBayesClassifier()
my_gauss.fit(X, y)
my_gauss.predict_proba([[-2, 5], [0,0], [6, -0.3]])

utganger

array([[8.06313823e-07, 1.36201957e-04, 9.99862992e-01], [1.00000000e+00, 4.23258691e-14, 1.92051255e-11], [4.30879705e-01, 5.69120295e-01, 9.66618838e-27]])

Spådommene ved hjelp av predict metoden er

# my_gauss.predict([[-2, 5], [0,0], [6, -0.3]])
array([2, 0, 1])

La oss nå bruke scikit-learn. Kaster inn litt kode

from sklearn.naive_bayes import GaussianNB gnb = GaussianNB()
gnb.fit(X, y)
gnb.predict_proba([[-2, 5], [0,0], [6, -0.3]])

rentene

array([[8.06314158e-07, 1.36201959e-04, 9.99862992e-01], [1.00000000e+00, 4.23259111e-14, 1.92051343e-11], [4.30879698e-01, 5.69120302e-01, 9.66619630e-27]])

Tallene ligner litt på tallene til klassifiseringen vår, men de er litt dårligere i de siste sifrene som vises. Gjorde vi noe galt? Nei. Scikit-learn-versjonen bruker bare en annen hyperparameter var_smoothing=1e-09 . Hvis vi setter denne til null, får vi nøyaktig våre tall. Perfekt!

Ta en titt på beslutningsregionene til klassifisereren vår. Jeg markerte også de tre punktene vi brukte for testing. At ett punkt nær grensen har bare 56.9 % sjanse for å tilhøre den røde klassen, som du kan se fra predict_proba utganger. De to andre punktene er klassifisert med mye høyere selvtillit.

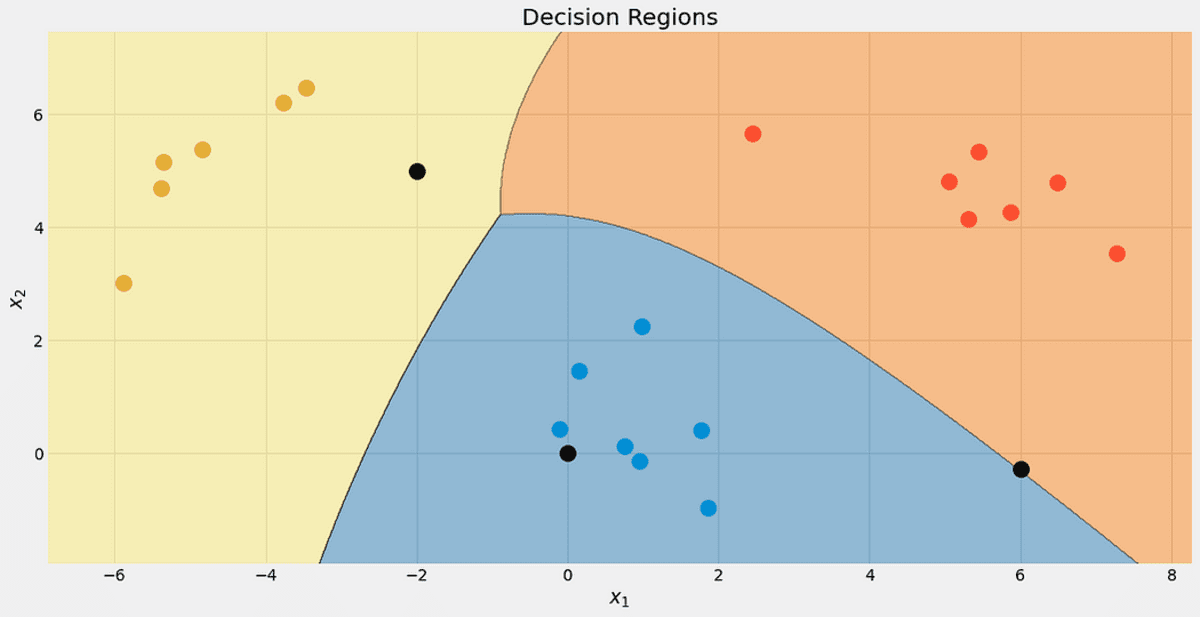
Gaussisk naiv Bayes, forklart

Vedtaksregionene med de 3 nye punktene. Bilde av forfatteren.

I denne artikkelen har vi lært hvordan den gaussiske naive Bayes-klassifikatoren fungerer og ga en intuisjon om hvorfor den ble designet på den måten - det er en direkte tilnærming for å modellere sannsynligheten for interesse. Sammenlign dette med logistisk regresjon: der modelleres sannsynligheten ved å bruke en lineær funksjon med en sigmoid-funksjon på toppen av den. Det er fortsatt en enkel modell, men den føles ikke like naturlig som en naiv Bayes-klassifiser.

Vi fortsatte med å regne ut noen få eksempler og samle noen nyttige kodebiter på veien. Til slutt har vi implementert en komplett Gaussisk naiv Bayes-klassifisering på en måte som fungerer godt med scikit-learn. Det betyr at du kan bruke den i rørledninger eller nettsøk, for eksempel.

Til slutt gjorde vi en liten fornuftssjekk ved å importere scikit-learns egen gaussiske naive Bayes-klassifiserer og teste om begge, vår og scikit-learns klassifiserer gir samme resultat. Denne testen var vellykket.

Dr. Robert Kübler er dataforsker ved Publicis Media og forfatter ved Towards Data Science.

original. Ompostet med tillatelse.