A kvantum-Wasserstein-távolság az elválasztható állapotok optimalizálása alapján

Újra kiadta Platón

Követő: 0

Tóth Géza^1,2,3,4,5 és Pitrik József^5,6,7

¹Elméleti fizika, Baszkföldi Egyetem UPV/EHU, ES-48080 Bilbao, Spanyolország
²EHU Quantum Center, University of the Baszkföld UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscay, Spanyolország
³Donostia Nemzetközi Fizikai Központ (DIPC), ES-20080 San Sebastián, Spanyolország
⁴IKERBASQUE, Baszk Tudományos Alapítvány, ES-48011 Bilbao, Spanyolország
⁵Szilárdtestfizikai és Optikai Intézet, Wigner Fizikai Kutatóközpont, HU-1525 Budapest
⁶Rényi Alfréd Matematikai Intézet, Reáltanoda u. 13-15., HU-1053 Budapest, Magyarország
⁷Budapesti Műszaki és Gazdaságtudományi Egyetem Matematikai Intézet Elemzési és Operációkutatási Osztály, Müegyetem rkp. 3., HU-1111 Budapest, Magyarország

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

A kvantum-Wasserstein-távolságot úgy határozzuk meg, hogy a csatolás optimalizálása inkább bipartit szeparálható állapotok felett történjen, mint általában bipartit kvantumállapotokon, és megvizsgáljuk a tulajdonságait. Meglepő módon azt találtuk, hogy az öntávolság a kvantum Fisher információhoz kapcsolódik. Bemutatunk egy optimális bipartit szeparálható állapotnak megfelelő transzport térképet. Megbeszéljük, hogy a bevezetett kvantum-Wasserstein-távolság hogyan kapcsolódik a kvantumösszefonódást detektáló kritériumokhoz. Varianciaszerű mennyiségeket definiálunk, amelyeket a kvantum Wasserstein-távolságból kaphatunk, ha a kvantumállapotok feletti minimalizálást maximalizálással helyettesítjük. Eredményeinket kiterjesztjük az általánosított kvantum Fisher információmennyiségek családjára.

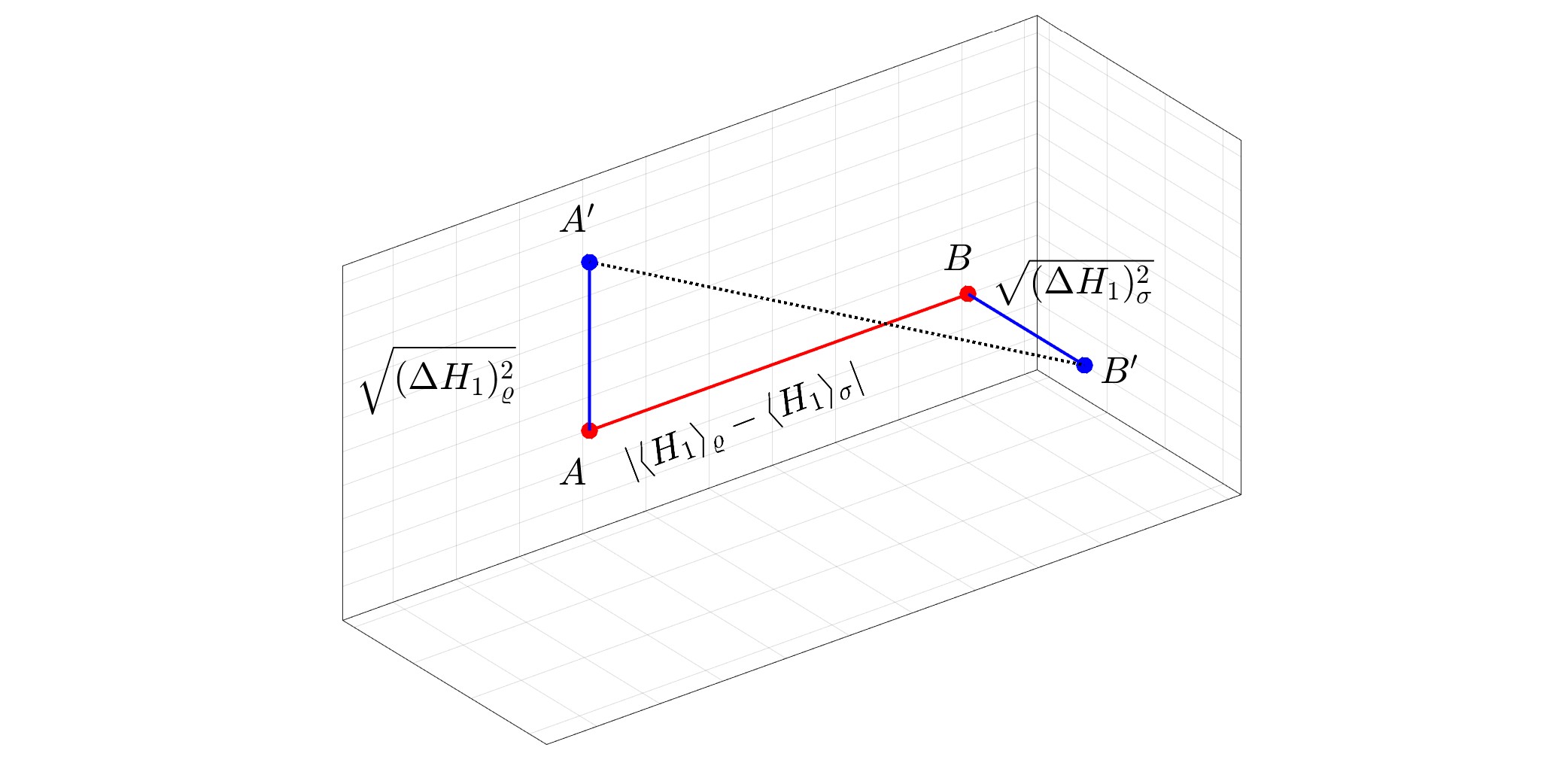
Kiemelt kép: A kvantum Wasserstein-távolság geometriai ábrázolása egy tiszta állapot $varrho$ és egy vegyes állapotú $sigma$ között $N=1.$ esetén A kvantum Wasserstein-távolság megegyezik a $1/sqrt2$-szorosával a szokásos euklideszi távolság $A'$ között és $B'.$

Népszerű összefoglaló

A mindennapi életben két város távolsága mondja meg, hány kilométert kell autóznunk egyikből a másikba. Az is jellemezhető, hogy milyen könnyen jutunk el egyik városból a másikba, ha az utunk során mérjük az üzemanyag-fogyasztást. Ez utóbbi abban az értelemben informatívabb, hogy az út domborzatához kapcsolódó utazási költséget tükrözi, azaz érzékeny a mögöttes mérőszámra. Ezután képzeljük el, hogy egy homokkupacot kell mozgatnunk egyik helyről a másikra, és az új halom más formát ölthet. A homok mozgatásának erőfeszítését ebben az esetben is a szállítás költségével jellemezhetjük.

A távolságok központi szerepet játszanak a matematikában, a fizikában és a mérnöki tudományokban. A valószínűségszámítás és a statisztika alapvető problémája a két valószínűségi eloszlás közötti távolság hasznos mértékeinek kidolgozása. Sajnos a valószínűségi eloszlások közötti távolság sok fogalma, mondjuk p(x) és q(x), akkor maximális, ha nem fedik át egymást, azaz az egyik mindig nulla, ha a másik nem nulla. Ez sok alkalmazásnál nem praktikus. Például, visszatérve a homok analógiájára, úgy tűnik, hogy két nem átfedő homokhalom egyformán távol van egymástól, függetlenül attól, hogy távolságuk 10 km vagy 100 km. Az optimális transzport elmélet egy módszer a valószínűségi eloszlások közötti távolság alternatív fogalmának, az úgynevezett Wasserstein-távolságnak a megalkotására. Akkor is lehet nem maximális, ha az eloszlások nem fedik át egymást, érzékeny a mögöttes mérőszámra (azaz a szállítás költségére), és lényegében azt az erőfeszítést fejezi ki, amelyre szükségünk van ahhoz, hogy áthelyezzük egymást, mintha homokdombok lennének.

A közelmúltban meghatározták a kvantum Wasserstein távolságot, általánosítva a klasszikus Wasserstein távolságot. Egy kétoldalú kvantumrendszer kvantumállapotai feletti költségfüggvény minimalizálásán alapul. A kvantumvilágban a fent említetthez hasonló tulajdonsággal rendelkezik. Ortogonális állapotok esetén lehet nem maximális, ami például akkor hasznos, ha kvantumadatokat kell tanítanunk egy algoritmusra.

Amint arra számíthatunk, a kvantum Wasserstein-távolságnak is vannak olyan tulajdonságai, amelyek nagyon eltérnek a klasszikus megfelelőjétől. Például, ha megmérjük egy kvantumállapot távolságát önmagától, akkor lehet, hogy nem nulla. Bár ez már most is elgondolkodtató, az is kiderült, hogy az öntávolság a Wigner-Yanase ferde információhoz kapcsolódik, amelyet 1963-ban vezetett be a Nobel-díjas EP Wigner, aki létfontosságú hozzájárulást jelent a kvantumfizika és az MM Yanase alapjaihoz.

Lapunkban még egy másik irányból vizsgáljuk ezt a rejtélyes leletet. A fent említett minimalizálást az úgynevezett szeparálható állapotokra korlátozzuk. Ezek azok a kvantumállapotok, amelyek nem tartalmaznak összefonódást. Azt találjuk, hogy az öntávolság a kvantum-Fischer-információvá válik, amely a kvantummetrológiában és a kvantumbecslés-elméletben központi jelentőségű mennyiség, és megjelenik például a híres Cramer-Rao kötésben. Egy ilyen Wasserstein-távolság tulajdonságainak vizsgálatával munkánk megnyitja az utat a kvantum-Wasserstein-távolság elméletének és a kvantumösszefonódás elméletének összekapcsolásához.

► BibTeX adatok

@cikk{Toth2023quantumwasserstein, doi = {10.22331/q-2023-10-16-1143}, url = {https://doi.org/10.22331/q-2023-10-16-1143}, cím { = {Quantum W}asserstein távolság elválasztható állapotok optimalizálása alapján}, szerző = {T{'{o}}th, G{'{e}}za és Pitrik, J{'{o}}zsef}, napló = {{ Quantum}}, issn = {2521-327X}, kiadó = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, kötet = {7}, oldal = {1143}, hónap = október, év = {2023} }

► Referenciák

[1] G. Monge. „Mémoire sur la théory des déblais et des remblais”. Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L. Kantorovitch. „A tömegek áttelepítéséről”. Vezetéstudomány 5, 1–4 (1958). url: http:///www.jstor.org/stable/2626967.
http:///www.jstor.org/stable/2626967

[3] Emmanuel Boissard, Thibaut Le Gouic és Jean-Michel Loubes. „Az elosztási sablon becslése wasserstein-metrikákkal”. Bernoulli 21, 740–759 (2015).
https:///doi.org/10.3150/13-bej585

[4] Oleg Butkovszkij. „Markov-folyamatok konvergenciájának szubgeometriai sebességei a Wasserstein-metrikában”. Ann. Appl. Valószínűleg. 24, 526–552 (2014).
https:///doi.org/10.1214/13-AAP922

[5] M. Hairer, J.-C. Mattingly és M. Scheutzow. „Aszimptotikus csatolás és Harris-tétel általános formája sztochasztikus késleltetési egyenletekre való alkalmazásokkal”. Valószínűleg. Elmélet Relat. Fields 149, 223–259 (2011).
https://doi.org/10.1007/s00440-009-0250-6

[6] M. Hairer és JC Mattingly. „Szektrális rések a Wasserstein-távolságban és a 2D sztochasztikus Navier-Stokes egyenletek”. Ann. Valószínűleg. 36, 2050–2091 (2008).
https:///doi.org/10.1214/08-AOP392

[7] A. Figalli, F. Maggi és A. Pratelli. „A mennyiségi izoperimetrikus egyenlőtlenségek tömegszállítási megközelítése”. Invent. Math. 182, 167–211. (2010).
https:///doi.org/10.1007/s00222-010-0261-z

[8] A. Figalli és F. Maggi. „A folyékony cseppek és kristályok alakjáról kis tömegű rendszerben”. Boltív. Adag. Mech. Anális. 201, 143–207 (2011).
https:///doi.org/10.1007/s00205-010-0383-x

[9] J. Lott és C. Villani. „Ricci görbület a metrikus mérési terekhez az optimális szállításon keresztül”. Ann. a Math. 169 (3), 903–991 (2009).
https:///doi.org/10.48550/arXiv.math/0412127

[10] Max-K. von Renesse és Karl-Theodor Sturm. „Szállítási egyenlőtlenségek, gradiensbecslések, entrópia és Ricci-görbület”. Comm. Pure Appl. Math. 58, 923–940 (2005).
https:///doi.org/10.1002/cpa.20060

[11] Karl-Theodor Sturm. „Az I metrikus mértékterek geometriájáról”. Acta Math. 196, 65–131 (2006).
https://doi.org/10.1007/s11511-006-0002-8

[12] Karl-Theodor Sturm. „A metrikus mértékterek geometriájáról II. Acta Math. 196, 133–177 (2006).
https://doi.org/10.1007/s11511-006-0003-7

[13] Benoı̂t Kloeckner. „A Wasserstein-terek geometriai vizsgálata: Euklideszi terek”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https:///doi.org/10.2422/2036-2145.2010.2.03

[14] Gehér György Pál, Titkos Tamás, Virosztek Dániel. „A wasserstein-terek izometrikus beágyazásain – a diszkrét eset”. J. Math. Anális. Appl. 480, 123435 (2019).
https:///doi.org/10.1016/j.jmaa.2019.123435

[15] Gehér György Pál, Titkos T., Virosztek Dániel. „A Wasserstein-terek izometrikus vizsgálata – az igazi vonal”. Trans. Amer. Math. Soc. 373, 5855–5883 (2020).
https:///doi.org/10.1090/tran/8113

[16] Gehér György Pál, Titkos Tamás, Virosztek Dániel. „A Wasserstein-terek izometriacsoportja: a Hilbert-eset”. J. London. Math. Soc. 106, 3865–3894 (2022).
https:///doi.org/10.1112/jlms.12676

[17] Gehér György Pál, Titkos Tamás, Virosztek Dániel. „A wasserstein tori és a gömbök izometrikus merevsége”. Mathematika 69, 20–32 (2023).
https:///doi.org/10.1112/mtk.12174

[18] Kiss Gergely és Titkos Tamás. „Wasserstein-terek izometrikus merevsége: A gráfmetrikus eset”. Proc. Am. Math. Soc. 150, 4083–4097 (2022).
https:///doi.org/10.1090/proc/15977

[19] Gehér György Pál, Titkos Tamás, Virosztek Dániel. „A másodfokú wasserstein-tér egzotikus izometriájáról a valódi vonal felett”. Lineáris algebra Appl. (2023).
https:///doi.org/10.1016/j.laa.2023.02.016

[20] S. Kolouri, SR Park és GK Rohde. „A Radon kumulatív eloszlási transzformációja és alkalmazása a képosztályozásban”. IEEE Trans. Képfeldolgozás. 25, 920–934 (2016).
https:///doi.org/10.1109/TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek és GK Rohde. „Lineáris optimális szállítási keretrendszer a képkészletek variációinak számszerűsítésére és megjelenítésére”. Int. J. Comput. Vis. 101, 254–269 (2013).
https:///doi.org/10.1007/s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. „Optimális tömegszállítás: jelfeldolgozás és gépi tanulási alkalmazások”. IEEE Signal Processing Magazine 34, 43–59 (2017).
https:///doi.org/10.1109/MSP.2017.2695801

[23] A. Gramfort, G. Peyré és M. Cuturi. „A neuroimaging adatok gyors optimális szállítási átlagolása”. Információfeldolgozás az orvosi képalkotásban. IPMI 2015. Lecture Notes in Computer Science 9123, 261–272 (2015).
https://doi.org/10.1007/978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu és X. Gu. „Alakosztályozás Wasserstein-távolság felhasználásával agymorfometriai elemzéshez”. Információfeldolgozás az orvosi képalkotásban. IPMI 2015. Lecture Notes in Computer Science 24, 411–423 (2015).
https://doi.org/10.1007/978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala és Léon Bottou. „Wasserstein generatív ellenséges hálózatok”. Doina Precup és Yee Whye Teh, szerkesztők, Proceedings of the 34th International Conference on Machine Learning. Proceedings of Machine Learning Research 70. kötete, 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] TA El Moselhy és YM Marzouk. „Bayes-i következtetés optimális térképekkel”. J. Comput. Phys. 231, 7815–7850 (2012).
https:///doi.org/10.1016/j.jcp.2012.07.022

[27] Gabriel Peyré és Marco Cuturi. „Számítógépes optimális szállítás: adattudományi alkalmazásokkal”. Megtalált. Trends Machine Learn. 11, 355–602 (2019).
https:///doi.org/10.1561/2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya és Tomaso A Poggio. „Tanulás wassersteini veszteséggel”. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama és R. Garnett, szerkesztők, Advances in Neural Information Processing Systems. 28. kötet Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[29] A. Ramdas, NG Trillos és M. Cuturi. „A Wasserstein-féle kétmintás tesztelésről és a nemparaméteres tesztek kapcsolódó családjairól”. Entrópia 19, 47. (2017).
https:///doi.org/10.3390/e19020047

[30] S. Srivastava, C. Li és DB Dunson. „Skálázható Bayes a Barycenteren keresztül a Wasserstein Space-ben”. J. Mach. Tanul. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski és Wojeciech Slomczynski. „A kvantumállapotok közötti Monge-távolság”. J. Phys. V: Matek. Gen. 31, 9095–9104 (1998).
https://doi.org/10.1088/0305-4470/31/45/009

[32] Karol Życzkowski és Wojciech Slomczynski. „A Monge-metrika a kvantumállapotok gömbjéről és geometriájáról”. J. Phys. V: Matek. Gen. 34, 6689–6722 (2001).
https://doi.org/10.1088/0305-4470/34/34/311

[33] Ingemar Bengtsson és Karol Życzkowski. „A kvantumállapotok geometriája: Bevezetés a kvantum-összefonódásba”. Cambridge University Press. (2006).
https:///doi.org/10.1017/CBO9780511535048

[34] P. Biane és D. Voiculescu. „A Wasserstein-metrika szabad valószínűségi analógja a nyomkövetési állapot térben”. GAFA, Geom. Funkció. Anális. 11, 1125–1138 (2001).
https://doi.org/10.1007/s00039-001-8226-4

[35] Eric A. Carlen és Jan Maas. „A 2-Wasserstein-metrika analógja a nem kommutatív valószínűségben, amely alatt a Fermionos Fokker-Planck egyenlet az entrópia gradiens áramlása”. Commun. Math. Phys. 331, 887–926 (2014).
https://doi.org/10.1007/s00220-014-2124-8

[36] Eric A. Carlen és Jan Maas. „Gradiens áramlás és entrópia egyenlőtlenségek kvantum Markov-félcsoportokhoz részletes mérleggel”. J. Funct. Anális. 273, 1810–1869 (2017).
https:///doi.org/10.1016/j.jfa.2017.05.003

[37] Eric A. Carlen és Jan Maas. „Nem kommutatív számítás, optimális transzport és funkcionális egyenlőtlenségek disszipatív kvantumrendszerekben”. J. Stat. Phys. 178, 319–378 (2020).
https:///doi.org/10.1007/s10955-019-02434-w

[38] Nilanjana Datta és Cambyse Rouzé. „Kvantumállapotok koncentrációja kvantumfunkcionális és szállítási költség egyenlőtlenségekből”. J. Math. Phys. 60, 012202 (2019).
https:///doi.org/10.1063/1.5023210

[39] Nilanjana Datta és Cambyse Rouzé. „A relatív entrópia, az optimális szállítás és a Fisher-információ összekapcsolása: A kvantum HWI egyenlőtlenség”. Ann. Henri Poincaré 21, 2115–2150 (2020).
https://doi.org/10.1007/s00023-020-00891-8

[40] François Golse, Clément Mouhot és Thierry Paul. „A kvantummechanika középteréről és klasszikus határairól”. Commun. Math. Phys. 343, 165–205 (2016).
https://doi.org/10.1007/s00220-015-2485-7

[41] François Golse és Thierry Paul. „A Schrödinger-egyenlet az átlagmezőben és a félklasszikus rendszerben”. Boltív. Adag. Mech. Anális. 223, 57–94 (2017).
https:///doi.org/10.1007/s00205-016-1031-x

[42] François Golse és Thierry Paul. „Hullámcsomagok és a kvadratikus Monge-Kantorovich távolság a kvantummechanikában”. Comptes Rendus Math. 356, 177–197 (2018).
https:///doi.org/10.1016/j.crma.2017.12.007

[43] François Golse. „A kvantum $N$-test probléma az átlagmezőben és a félklasszikus rendszerben”. Phil. Trans. R. Soc. A 376, 20170229 (2018).
https:///doi.org/10.1098/rsta.2017.0229

[44] E. Caglioti, F. Golse és T. Paul. „A kvantumoptimális szállítás olcsóbb”. J. Stat. Phys. 181, 149–162 (2020).
https://doi.org/10.1007/s10955-020-02571-7

[45] Emanuele Caglioti, François Golse és Thierry Paul. „A kvantumsűrűségek optimális szállítása felé”. arXiv:2101.03256 (2021).
https:///doi.org/10.48550/arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma és Dario Trevisan. „Kvantumoptimális transzport kvantumcsatornákkal”. Ann. Henri Poincaré 22, 3199–3234 (2021).
https://doi.org/10.1007/s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan és Seth Lloyd. „Az 1-es rendű kvantum Wasserstein-távolság”. IEEE Trans. Inf. Theory 67, 6627–6643 (2021).
https:///doi.org/10.1109/TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole és Karol Życzkowski. „Quantum Monge–Kantorovich probléma és a sűrűségmátrixok közötti szállítási távolság”. Phys. Rev. Lett. 129, 110402 (2022).
https:///doi.org/10.1103/PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland és Karol Życzkowski. „Kvantumoptimális szállítás”. arXiv:2105.06922 (2021).
https:///doi.org/10.48550/arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein és K. Życzkowski. „A kvantum-2-Wasserstein-távolság monotonitása”. J. Phys. V: Matek. Theor. 56, 095301 (2023).
https://doi.org/10.1088/1751-8121/acb9c8

[51] Gehér György Pál, Pitrik József, Titkos Tamás, Virosztek Dániel. „Kvantum Wasserstein izometriák a qubit állapottéren”. J. Math. Anális. Appl. 522, 126955 (2023).
https:///doi.org/10.1016/j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe és Seth Lloyd. „A kvantumáramkörök Wasserstein komplexitása”. arXiv: 2208.06306 (2022).
https:///doi.org/10.48550/arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu és Seth Lloyd. „Kvantumadatok tanulása a kvantumföldmozgató távolságával”. Quantum Sci. Technol. 7, 045002 (2022).
https://doi.org/10.1088/2058-9565/ac79c9

[54] EP Wigner és Mutsuo M. Yanase. „A disztribúciók információtartalma”. Proc. Natl. Acad. Sci. USA 49, 910–918 (1963).
https:///doi.org/10.1073/pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki és Karol Horodecki. „Kvantumösszefonódás”. Rev. Mod. Phys. 81, 865–942 (2009).
https:///doi.org/10.1103/RevModPhys.81.865

[56] Otfried Gühne és Tóth Géza. „Összefonódás észlelése”. Phys. Rep. 474, 1–75 (2009).
https:///doi.org/10.1016/j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik és Marcus Huber. „Összefonódási tanúsítás az elmélettől a kísérletig”. Nat. Rev. Phys. 1, 72–87 (2019).
https://doi.org/10.1038/s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd és Lorenzo Maccone. „Kvantum-növelt mérések: A szabványos kvantumhatár túllépése”. Science 306, 1330–1336 (2004).
https:///doi.org/10.1126/science.1104149

[59] Matteo GA Párizs. „Kvantumbecslés kvantumtechnológiához”. Int. J. Quant. Inf. 07, 125–137 (2009).
https:///doi.org/10.1142/S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna és Jan Kolodynski. „Negyedik fejezet – Kvantumhatárok az optikai interferometriában”. Prog. Optika 60, 345–435 (2015). arXiv:1405.7703.
https:///doi.org/10.1016/bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze és Augusto Smerzi. „A fázisbecslés kvantumelmélete”. In GM Tino és MA Kasevich, szerkesztők, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Course 188, Varenna). 691–741. oldal. IOS Press, Amszterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Tóth Géza és Petz Dénes. „A variancia és a kvantum Fisher-információ extrém tulajdonságai”. Phys. Rev. A 87, 032324 (2013).
https:///doi.org/10.1103/PhysRevA.87.032324

[63] Sixia Yu. „A kvantum Fisher információ mint a variancia domború teteje”. arXiv:1302.5311 (2013).
https:///doi.org/10.48550/arXiv.1302.5311
arXiv: 1302.5311

[64] Tóth Géza és Florian Fröwis. „Bizonytalansági kapcsolatok a varianciával és a kvantum Fisher-információval a sűrűségmátrixok konvex dekompozíciói alapján”. Phys. Rev. Research 4, 013075 (2022).
https:///doi.org/10.1103/PhysRevResearch.4.013075

[65] Shao-Hen Chiew és Manuel Gessner. „Az összeg-bizonytalansági kapcsolatok javítása a kvantum Fisher információval”. Phys. Rev. Research 4, 013076 (2022).
https:///doi.org/10.1103/PhysRevResearch.4.013076

[66] CW Helstrom. „Kvantumdetektálás és becslés elmélete”. Academic Press, New York. (1976). url: www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5.
https://www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5

[67] AS Holevo. „A kvantumelmélet valószínűségi és statisztikai vonatkozásai”. Észak-Hollandia, Amszterdam. (1982).

[68] Samuel L. Braunstein és Carlton M. Caves. „Statisztikai távolság és a kvantumállapotok geometriája”. Phys. Rev. Lett. 72, 3439-3443 (1994).
https:///doi.org/10.1103/PhysRevLett.72.3439

[69] Samuel L Braunstein, Carlton M Caves és Gerard J Milburn. „Általános bizonytalansági viszonyok: elmélet, példák és Lorentz-invariancia”. Ann. Phys. 247, 135–173 (1996).
https:///doi.org/10.1006/aphy.1996.0040

[70] Petz Dénes. „Kvantuminformációs elmélet és kvantumstatisztika”. Springer, Berlin, Heilderberg. (2008).
https://doi.org/10.1007/978-3-540-74636-2

[71] Tóth Géza és Iagoba Apellaniz. „Kvantummetrológia kvantuminformációtudományi szemszögből”. J. Phys. V: Matek. Theor. 47, 424006 (2014).
https://doi.org/10.1088/1751-8113/47/42/424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied és Philipp Treutlein. „Kvantummetrológia atomi együttesek nem klasszikus állapotaival”. Rev. Mod. Phys. 90, 035005 (2018).
https:///doi.org/10.1103/RevModPhys.90.035005

[73] Marco Barbieri. „Optikai kvantummetrológia”. PRX Quantum 3, 010202 (2022).
https:///doi.org/10.1103/PRXQuantum.3.010202

[74] Léka Zoltán és Petz Dénes. „A mátrix varianciáinak néhány dekompozíciója”. Valószínűleg. Math. Statisztika. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Petz Dénes és Virosztek Dániel. „A mátrixvarianciák jellemzési tétele”. Acta Sci. Math. (Szeged) 80, 681–687 (2014).
https:///doi.org/10.14232/actasm-013-789-z

[76] Akio Fujiwara és Hiroshi Imai. „A kvantumcsatornák sokaságán átívelő szálköteg és alkalmazása a kvantumstatisztikában”. J. Phys. V: Matek. Theor. 41, 255304 (2008).
https://doi.org/10.1088/1751-8113/41/25/255304

[77] BM Escher, RL de Matos Filho és L. Davidovich. „Általános keretrendszer a zajos kvantum-bővített metrológia végső pontossági határának becsléséhez”. Nat. Phys. 7, 406–411 (2011).
https:///doi.org/10.1038/nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński és Mădălin Guţă. „A megfoghatatlan Heisenberg-határ a kvantum-bővített metrológiában”. Nat. Commun. 3, 1063 (2012).
https:///doi.org/10.1038/ncomms2067

[79] Iman Marvian. „A kvantumhalász információ operatív értelmezése a kvantumtermodinamikában”. Phys. Rev. Lett. 129, 190502 (2022).
https:///doi.org/10.1103/PhysRevLett.129.190502

[80] Reinhard F. Werner. „Kvantumállapotok Einstein-Podolsky-Rosen korrelációkkal, amelyek rejtett változós modellt engednek meg”. Phys. Rev. A 40, 4277–4281 (1989).
https:///doi.org/10.1103/PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss és M. Lewenstein. „Kvantumkorrelációk megkülönböztethetetlen részecskék rendszereiben”. Ann. Phys. 299, 88–127 (2002).
https:///doi.org/10.1006/aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui és Nobuhiro Yonezawa. „Csereszimmetria és többrészes összefonódás”. Phys. Rev. A 78, 052105 (2008).
https:///doi.org/10.1103/PhysRevA.78.052105

[83] Pawel Horodecki. „Elválaszthatósági kritérium és elválaszthatatlan vegyes állapotok pozitív részleges transzpozícióval”. Phys. Lett. A 232, 333–339 (1997).
https://doi.org/10.1016/S0375-9601(97)00416-7

[84] Asher Peres. „Sűrűségmátrixok elválaszthatósági kritériuma”. Phys. Rev. Lett. 77, 1413–1415 (1996).
https:///doi.org/10.1103/PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki és Ryszard Horodecki. „A kötött összefonódás aktiválható”. Phys. Rev. Lett. 82, 1056-1059 (1999).
https:///doi.org/10.1103/PhysRevLett.82.1056

[86] Tóth Géza és Vértesi Tamás. "A pozitív részleges transzponált kvantumállapotok hasznosak a metrológiában." Phys. Rev. Lett. 120, 020506 (2018).
https:///doi.org/10.1103/PhysRevLett.120.020506

[87] Scott Hill és William K. Wootters. „Egy kvantumbitpár összefonódása”. Phys. Rev. Lett. 78, 5022-5025 (1997).
https:///doi.org/10.1103/PhysRevLett.78.5022

[88] William K. Wootters. „Két qubit tetszőleges állapotának kialakulásának összefonódása”. Phys. Rev. Lett. 80, 2245–2248 (1998).
https:///doi.org/10.1103/PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal és Armin Uhlmann. „A segítség összefonódása”. quant-ph/9803033 (1998).
https:///doi.org/10.48550/arXiv.quant-ph/9803033
arXiv:quant-ph/9803033

[90] John A. Smolin, Frank Verstraete és Andreas Winter. „A segítségnyújtás és a többoldalú állami lepárlás összefonódása”. Phys. Rev. A 72, 052317 (2005).
https:///doi.org/10.1103/PhysRevA.72.052317

[91] Holger F. Hofmann és Shigeki Takeuchi. „A lokális bizonytalansági viszonyok megsértése, mint az összefonódás jele”. Phys. Rev. A 68, 032103 (2003).
https:///doi.org/10.1103/PhysRevA.68.032103

[92] Otfried Gühne. „Az összefonódás jellemzése bizonytalansági kapcsolatokon keresztül”. Phys. Rev. Lett. 92, 117903 (2004).
https:///doi.org/10.1103/PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth, and Peter Adam. „A lokális bizonytalansági kapcsolatokon alapuló összefonódási kritériumok szigorúan erősebbek, mint a kiszámítható keresztnorma-kritérium”. Phys. Rev. A 74, 010301 (2006).
https:///doi.org/10.1103/PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza és Tóth Géza. „Centrifugálási egyenlőtlenségek önkényes pörgetéshez”. Phys. Rev. Lett. 107, 240502 (2011).
https:///doi.org/10.1103/PhysRevLett.107.240502

[95] AR Edmonds. „Szögimpulzus a kvantummechanikában”. Princeton University Press. (1957).
https:///doi.org/10.1515/9781400884186

[96] Tóth Géza. „Összefonódás detektálása bozonikus atomok optikai rácsában kollektív mérésekkel”. Phys. Rev. A 69, 052327 (2004).
https:///doi.org/10.1103/PhysRevA.69.052327

[97] Tóth Géza, Christian Knapp, Otfried Gühne és Hans J. Briegel. „Az optimális spin-sajtolási egyenlőtlenségek észlelik a kötött összefonódást a spin modellekben”. Phys. Rev. Lett. 99, 250405 (2007).
https:///doi.org/10.1103/PhysRevLett.99.250405

[98] Tóth Géza és Morgan W Mitchell. „Makroszkópikus szingulett állapotok generálása atomi együttesekben”. Új J. Phys. 12, 053007 (2010).
https://doi.org/10.1088/1367-2630/12/5/053007

[99] Tóth Géza. „Többrészes összefonódás észlelése szimmetrikus Dicke-állapotok közelében”. J. Opt. Soc. Am. B 24, 275–282 (2007).
https:///doi.org/10.1364/JOSAB.24.000275

[100] Tóth Géza, Tobias Moroder és Otfried Gühne. „A domború tetőösszefonódási intézkedések értékelése”. Phys. Rev. Lett. 114, 160501 (2015).
https:///doi.org/10.1103/PhysRevLett.114.160501

[101] Lieven Vandenberghe és Stephen Boyd. „Félig határozott programozás”. SIAM Review 38, 49–95 (1996).
https:///doi.org/10.1137/1038003

[102] Tóth Géza. „Többrészes összefonódás és nagy pontosságú metrológia”. Phys. Rev. A 85, 022322 (2012).
https:///doi.org/10.1103/PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé és Augusto Smerzi. „Fisher-információ és többrészecske-összefonódás”. Phys. Rev. A 85, 022321 (2012).
https:///doi.org/10.1103/PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki, and Ryszard Horodecki. „A rejtett metrológiai hasznosság aktiválása”. Phys. Rev. Lett. 125, 020402 (2020).
https:///doi.org/10.1103/PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo és Federico M. Spedalieri. „Az elválasztható és összefonódott állapotok megkülönböztetése”. Phys. Rev. Lett. 88, 187904 (2002).
https:///doi.org/10.1103/PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo és Federico M. Spedalieri. „Az elkülöníthetőségi kritériumok teljes családja”. Phys. Rev. A 69, 022308 (2004).
https:///doi.org/10.1103/PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo és Federico M. Spedalieri. „Többrészes összefonódás észlelése”. Phys. Rev. A 71, 032333 (2005).
https:///doi.org/10.1103/PhysRevA.71.032333

[108] Harold Ollivier és Wojciech H. Zurek. „Kvantumdiszkord: A korrelációk kvantumának mértéke”. Phys. Rev. Lett. 88, 017901 (2001).
https:///doi.org/10.1103/PhysRevLett.88.017901

[109] L. Henderson és V. Vedral. „Klasszikus, kvantum és teljes összefüggések”. J. Phys. V: Matek. Gen. 34, 6899 (2001).
https://doi.org/10.1088/0305-4470/34/35/315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) és Ujjwal Sen. „Kvantumvihar és szövetségesei: a közelmúlt fejlődésének áttekintése”. Rep. Prog. Phys. 81, 024001 (2017).
https:///doi.org/10.1088/1361-6633/aa872f

[111] Petz Dénes. „Kovariancia és Fisher-információ a kvantummechanikában”. J. Phys. V: Matek. Gen. 35, 929 (2002).
https://doi.org/10.1088/0305-4470/35/4/305

[112] Paolo Gibilisco, Fumio Hiai és Petz Dénes. „Kvantumkovariancia, kvantum-Fischer-információ és a bizonytalansági viszonyok”. IEEE Trans. Inf. Theory 55, 439–443 (2009).
https:///doi.org/10.1109/TIT.2008.2008142

[113] D. Petz és C. Ghinea. „Bevezetés a kvantum-Fischer-információkba”. 27. évfolyam, 261–281. Tudományos Világ. (2011).
https:///doi.org/10.1142/9789814338745_0015

[114] Frank Hansen. „Metric korrigált ferde információ”. Proc. Natl. Acad. Sci. USA 105, 9909–9916 (2008).
https:///doi.org/10.1073/pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami és Frank Hansen. „A lokális kvantumbizonytalanság és az interferometrikus teljesítmény egységes megközelítése metrikusan kiigazított ferde információval”. Entrópia 23, 263 (2021).
https:///doi.org/10.3390/e23030263

[116] MATLAB. „9.9.0.1524771(r2020b)”. A MathWorks Inc. Natick, Massachusetts (2020).

[117] MOSEK ApS. „A MOSEK optimalizálási eszköztár a MATLAB kézikönyvhöz. 9.0” verzió. (2019). url: docs.mosek.com/9.0/toolbox/index.html.
https:///docs.mosek.com/9.0/toolbox/index.html

[118] J. Löfberg. „YALMIP: Eszköztár a MATLAB modellezéshez és optimalizálásához”. In Proceedings of the CACSD Conference. Taipei, Tajvan (2004).

[119] Tóth Géza. „QUBIT4MATLAB V3.0: Programcsomag kvantuminformáció-tudományhoz és kvantumoptikához a MATLAB számára”. Comput. Phys. Commun. 179, 430–437 (2008).
https:///doi.org/10.1016/j.cpc.2008.03.007

[120] A QUBIT4MATLAB csomag elérhető a https:///www.mathworks.com/matlabcentral/fileexchange/8433 címen és a https://gtoth.eu/qubit4matlab.html személyes honlapon.
https:///www.mathworks.com/matlabcentral/fileexchange/8433

Idézi

[1] Laurent Lafleche, „Quantum Optimal Transport and Weak Topologies”, arXiv: 2306.12944, (2023).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2023-10-16 14:47:44). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

Nem sikerült lekérni Az adatok által hivatkozott kereszthivatkozás utolsó próbálkozáskor 2023-10-16 14:47:42: Nem sikerült lekérni a 10.22331/q-2023-10-16-1143 hivatkozás által hivatkozott adatokat a Crossref-től. Ez normális, ha a DOI-t nemrég regisztrálták.

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
PlatoData.Network Vertical Generative Ai. Erősítse meg magát. Hozzáférés itt.
PlatoAiStream. Web3 Intelligence. Felerősített tudás. Hozzáférés itt.
PlatoESG. Carbon, CleanTech, Energia, Környezet, Nap, Hulladékgazdálkodás. Hozzáférés itt.
PlatoHealth. Biotechnológiai és klinikai vizsgálatok intelligencia. Hozzáférés itt.
Forrás: https://quantum-journal.org/papers/q-2023-10-16-1143/

Időbélyeg: Október 16, 2023

Időbélyeg: 6. október 2022.

Újra kiadta Platón

Adaptív mérési szűrő: hatékony stratégia a kvantum Markov-láncok optimális becsléséhez

Összefonódási dinamika U(1) szimmetrikus hibrid kvantumautomata áramkörökben

Elfogultságra szabott kvantum LDPC kódok

Mikor érkezik egy részecske?

A Macaulay-mátrix megközelítés korlátai a HHL algoritmus használatához többváltozós polinomrendszerek megoldására

Kvantuminformáció felső kvarkokkal a QCD-ben

Kvantum üzenettovábbítási algoritmus az optimális és hatékony dekódoláshoz

Minimális kommunikációs költség az összegabalyodott qubitek szimulálásához

Kétszintű mechanikai rendszer kvantummanipulációja

Hőállapot-előkészítés kerekítési ígéretekkel

Kvantumvariációs tanulás kvantumhibajavító kódokhoz

Rólunk

Vertical Search & Ai

Emelvény

Maradjon kapcsolatban

Fiók