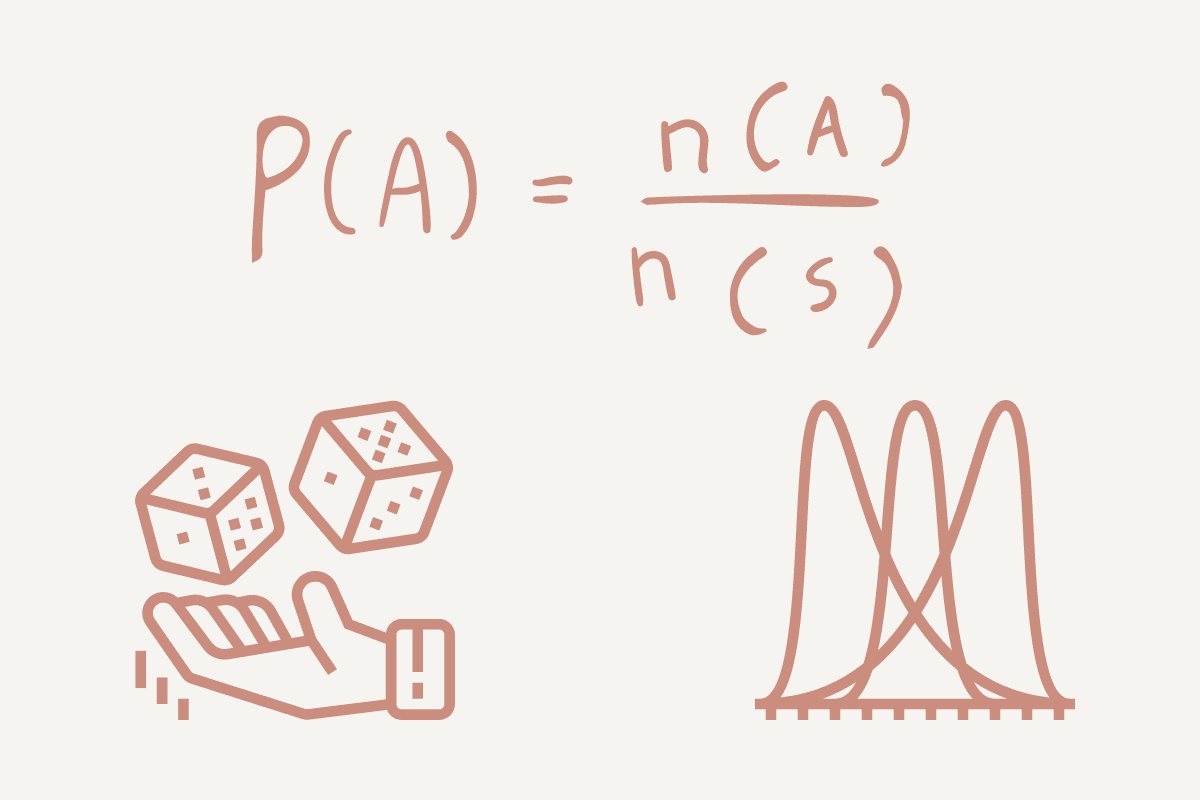
A valószínűség jelentősége az adattudományban

Újra kiadta Platón

Követő: 0

A valószínűség jelentősége az adattudományban
A kép szerzője

Adattudósként tudnia kell az eredmények pontosságát az érvényesség biztosítása érdekében. Az adattudományi munkafolyamat egy tervezett projekt, ellenőrzött feltételekkel. Lehetővé teszi, hogy felmérje az egyes szakaszokat, és azt, hogy az hogyan hatott az eredményre.

A valószínűség egy esemény/valami történés valószínűségének mértéke. Fontos eleme a prediktív elemzésnek, amely lehetővé teszi az eredmény mögött meghúzódó számítási matematika feltárását.

Egy egyszerű példával élve nézzük meg az érme feldobását: vagy fejek (H) vagy farok (T). A valószínűsége az lesz, hogy hány módon fordulhat elő egy esemény, osztva a lehetséges kimenetelek számával.

Ha meg akarjuk találni a fejek valószínűségét, akkor ez 1 (fej) / 2 (fejek és farok) = 0.5.
Ha meg akarjuk találni a farok valószínűségét, akkor ez 1 (farok) / 2 (fejek és farok) = 0.5.

De nem akarjuk összekeverni a valószínűséget és a valószínűséget – van különbség. A valószínűség egy adott esemény vagy eredmény bekövetkezésének mértéke. A valószínűséget akkor alkalmazzuk, ha növelni akarjuk egy adott esemény vagy kimenetel bekövetkezésének esélyét.

Hogy ezt lebontsuk – a valószínűség a lehetséges eredményekről, míg a valószínűség a hipotézisekről szól.

Egy másik ismerendő kifejezés az „egymást kizáró események”. Ezek olyan események, amelyek nem egy időben történnek. Például nem lehet egyszerre jobbra és balra menni. Vagy ha feldobunk egy érmét, akkor vagy kaphatunk fejet vagy farkot, nem mindkettőt.

A valószínűség típusai

Elméleti valószínűség: ez egy esemény bekövetkezésének valószínűségére összpontosít, és az érvelés alapjain alapul. Az elméletet használva az eredmény a várható érték. A fej és a farok példáját használva a fejre való leszállás elméleti valószínűsége 0.5 vagy 50%.
Kísérleti valószínűség: ez arra összpontosít, hogy milyen gyakran fordul elő egy esemény a kísérlet időtartama alatt. A fej és a farok példáját használva – ha 10-szer dobnánk fel egy érmét, és 6-szor a fejeken landolna, akkor a kísérleti valószínűsége annak, hogy az érme fejeken landol, 6/10 vagy 60% lenne.

A feltételes valószínűség egy esemény/eredmény bekövetkezésének lehetősége egy létező esemény/eredmény alapján. Például, ha Ön egy biztosítótársaságnál dolgozik, érdemes megkeresnie annak valószínűségét, hogy valaki ki tudja fizetni a biztosítását, azzal a feltétellel, hogy lakáshitelt vett fel.

A feltételes valószínűség segítségével az adatkutatók pontosabb modelleket és kimeneteket állíthatnak elő az adatkészlet más változóinak felhasználásával.

A valószínűségi eloszlás egy statisztikai függvény, amely segít leírni egy valószínűségi változó lehetséges értékeit és valószínűségeit egy adott tartományon belül. A tartománynak megvannak a lehetséges minimum- és maximumértékei, és az, hogy ezek hol jelennek meg egy eloszlási grafikonon, a statisztikai tesztektől függ.

A projektben használt adatok típusától függően kitalálhatja, hogy milyen típusú terjesztést használ. Két kategóriába sorolom őket: diszkrét eloszlás és folyamatos eloszlás.

Diszkrét elosztás

A diszkrét eloszlás az, amikor az adatok csak bizonyos értékeket vehetnek fel, vagy korlátozott számú kimenetelük van. Például, ha dobott egy kockát, a korlátozott értékek 1, 2, 3, 4, 5 és 6.

Különféle diszkrét elosztások léteznek. Például:

Diszkrét egyenletes eloszlás amikor minden eredmény egyformán valószínű. Ha a hatoldalú kockadobás példáját használjuk, akkor egyenlő a valószínűsége annak, hogy 1, 2, 3, 4, 5 vagy 6 – ⅙-re tud leszállni. A diszkrét egyenletes eloszlással azonban az a probléma, hogy nem biztosít számunkra releváns információkat, amelyeket az adatkutatók felhasználhatnak és alkalmazhatnak.
Bernoulli-eloszlás A diszkrét eloszlás egy másik típusa, ahol a kísérletnek csak két lehetséges kimenetele van, vagy igen vagy nem, 1 vagy 2, igaz vagy hamis. Ezt érme feldobásakor használhatjuk, ez akár fej, akár farok. A Bernoulli-eloszlás használatakor megvan az egyik eredmény valószínűsége (p), és ezt le tudjuk vonni az (1-p) teljes valószínűségből (1).
Binomiális eloszlás Bernoulli események sorozata, és az a diszkrét valószínűségi eloszlás, amely csak két lehetséges eredményt tud produkálni egy kísérletben, vagy sikert vagy kudarcot. Érme feldobásakor az érme feldobásának valószínűsége mindig 1.5 vagy ½ lesz minden kísérletben.
Poisson-eloszlás annak eloszlása, hogy egy esemény valószínűleg hányszor fog bekövetkezni egy meghatározott időszakon vagy távolságon belül. Ahelyett, hogy egy eseményre összpontosítana, egy adott intervallumban előforduló esemény gyakoriságára összpontosít. Például, ha minden nap 12 órakor 11 autó megy le egy adott úton, a Poisson-eloszlás segítségével kiszámolhatjuk, hány autó megy le azon az úton délelőtt 11 órakor egy hónapban.

Folyamatos terjesztés

Ellentétben a véges kimenetelű diszkrét eloszlásokkal, a folytonos eloszlások folytonos kimenetelűek. Ezek az eloszlások jellemzően görbeként vagy vonalként jelennek meg a grafikonon, mivel az adatok folyamatosak.

Normális eloszlás lehet, hogy hallottál róla, mivel ez a leggyakrabban használt. Ez az értékek szimmetrikus eloszlása az átlag körül, ferdeség nélkül. Az adatok ábrázoláskor harang alakot követnek, ahol a középső tartomány az átlag. Például az olyan jellemzők, mint a magasság és az IQ-pontszámok normál eloszlást követnek.
T-Distribution a folytonos eloszlás olyan típusa, amelyet akkor használnak, ha a sokaság szórása (σ) ismeretlen és a minta mérete kicsi (n<30). Ugyanazt az alakot követi, mint egy normál eloszlás, a haranggörbe. Például, ha azt nézzük, hány tábla csokit adtak el egy nap, akkor a normál eloszlást használnánk. Ha azonban azt akarjuk megnézni, hogy egy adott órán hány darab kelt el, akkor t-elosztást használunk.
Exponenciális eloszlás a folytonos valószínűségi eloszlás egyik fajtája, amely az esemény bekövetkeztéig eltelt időre összpontosít. Például érdemes lehet megvizsgálni a földrengéseket, és használhatjuk az exponenciális eloszlást. Ettől a ponttól a földrengésig eltelt idő. Az exponenciális eloszlás görbe vonalként van ábrázolva, és a valószínűségeket exponenciálisan ábrázolja.

A fentiekből láthatja, hogy az adattudósok hogyan használhatják fel a valószínűséget, hogy többet tudjanak meg az adatokról és válaszoljanak kérdésekre. Az adattudósok számára nagyon hasznos, ha ismerik és megértik egy esemény bekövetkezésének esélyeit, és nagyon hatékonyak lehetnek a döntéshozatali folyamatban.

Folyamatosan fog dolgozni az adatokkal, és többet kell megtudnia róluk, mielőtt bármilyen elemzést végezne. Az adatelosztást tekintve sok információval gazdagodhat, és ez felhasználható a feladat, a folyamat és a modell beállításához, hogy megfeleljen az adatelosztásnak.

Ez csökkenti az adatok megértésére fordított időt, hatékonyabb munkafolyamatot biztosít, és pontosabb eredményeket produkál.

Az adattudomány sok fogalma a valószínűségszámítás alapjain alapul.

Nisha Arya adattudós és szabadúszó műszaki író. Különösen érdekli az adattudományi karriertanácsadás vagy oktatóanyagok, valamint elméleti alapú ismeretek nyújtása a Data Science területén. Azt is szeretné feltárni, hogy a mesterséges intelligencia milyen különböző módokon járulhat hozzá az emberi élet hosszú élettartamához. Szívesen tanuló, aki igyekszik bővíteni műszaki ismereteit és íráskészségét, miközben segít másoknak.