Gaussian Naive Bayes, magyarázat

Egy Gauss-féle naiv Bayes-osztályozó döntési tartománya. Kép a szerzőtől.

Azt hiszem, ez egy klasszikus minden adattudományi pálya elején: a Naiv Bayes osztályozó. Vagy inkább azt kellene mondanom család a naiv Bayes osztályozók közül, mivel sokféle ízben kaphatók. Például létezik egy multinomiális naiv Bayes, egy Bernoulli naiv Bayes és egy Gauss-féle naiv Bayes osztályozó is, amelyek mindegyike csak egy apró részletben különbözik, amint megtudjuk. A naiv Bayes-algoritmusok tervezése meglehetősen egyszerű, de hasznosnak bizonyultak számos összetett valós helyzetben.

Ebben a cikkben megtanulhatja

• hogyan működnek a naiv Bayes osztályozók,
• miért van értelme meghatározni őket úgy, ahogy vannak és
• hogyan valósítsuk meg őket Pythonban a NumPy segítségével.

A kódot megtalálod az én Githubom.

Egy kicsit segíthet, ha megnézem a Bayes-statisztikákról szóló primeremet Gyengéd bevezetés a Bayes-i következtetésbe hogy megszokja a Bayes-képletet. Mivel az osztályozót scikit tanulás-konform módon fogjuk megvalósítani, ezért érdemes megnézni cikkemet is Készítse el saját egyéni scikit-learn regresszióját. Azonban a scikit-learn overhead elég kicsi, és így is képesnek kell lennie követni.

Elkezdjük a naiv Bayes-osztályozás elképesztően egyszerű elméletének feltárását, majd rátérünk a megvalósításra.

Mire vagyunk igazán kíváncsiak az osztályozás során? Mit csinálunk valójában, mi a bemenet és a kimenet? A válasz egyszerű:

Ha adott egy x adatpont, mekkora a valószínűsége annak, hogy x valamilyen c osztályba tartozik?

Csak ennyivel akarunk válaszolni bármilyen osztályozás. Ezt az állítást közvetlenül modellezheti feltételes valószínűségként: p(c|x).

Például ha vannak

• 3 osztályok c₁, c₂, c₃és
• x 2 jellemzőből áll x₁, x₂,

egy osztályozó eredménye valami ilyesmi lehet p(c₁|x₁, x₂)=0.3, p(c₂|x₁, x₂)=0.5 és p(c₃|x₁, x₂)=0.2. Ha egyetlen címkét látunk kimenetként, akkor azt választjuk, amelyik a legnagyobb valószínűséggel, pl c₂ itt 50%-os valószínűséggel.

A naiv Bayes-osztályozó megpróbálja közvetlenül kiszámítani ezeket a valószínűségeket.

Naiv Bayes

Rendben, adott egy adatpont x, szeretnénk kiszámolni p(c|x) minden osztály számára c majd adja ki a c a legnagyobb valószínűséggel. A képletekben ezt gyakran úgy látja

Kép a szerzőtől.

Jegyzet: max p(c|x) a maximális valószínűséget adja vissza, míg az argmax p(c|x) visszaadja a c ezzel a legnagyobb valószínűséggel.

De mielőtt optimalizálni tudnánk p(c|x), ki kell tudnunk számolni. Ehhez használjuk Bayes tétele:

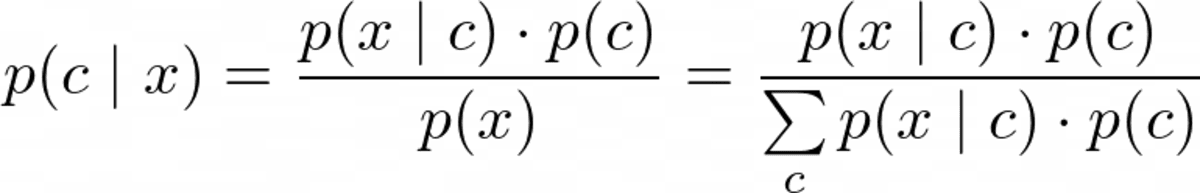
Bayes-tétel. Kép a szerzőtől.

Ez a naiv Bayes Bayes része. De most a következő problémánk van: Mik azok p(x|c) És p(c)?

Erről szól a naiv Bayes-osztályozó képzése.

A képzés

Mindennek szemléltetésére használjunk egy játék adatkészletet két igazi vonás x₁, x₂és három osztály c₁, c₂, c₃ az alábbiakban.

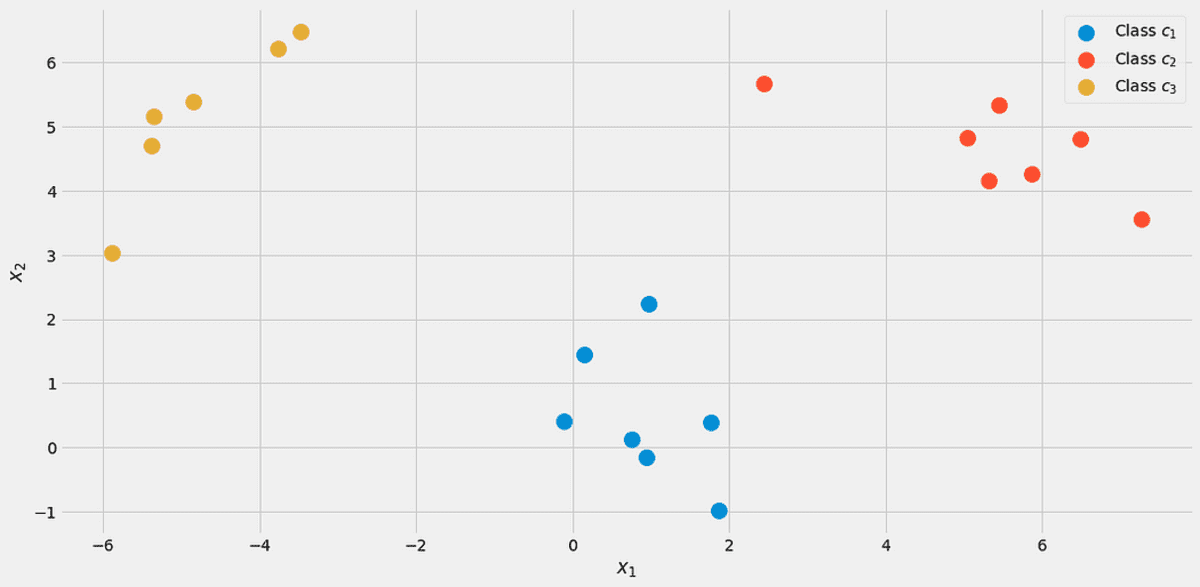
Az adatok, megjelenítve. Kép a szerzőtől.

Ezt a pontos adatkészletet a következőn keresztül hozhatja létre

from sklearn.datasets import make_blobs X, y = make_blobs(n_samples=20, centers=[(0,0), (5,5), (-5, 5)], random_state=0)

Kezdjük a osztályvalószínűség p(c), annak a valószínűsége, hogy valamelyik osztály c a címkézett adatkészletben figyelhető meg. Ennek becslésének legegyszerűbb módja az, ha kiszámítjuk az osztályok relatív gyakoriságát, és felhasználjuk őket valószínűségként. Adatkészletünk segítségével megtudhatjuk, hogy ez pontosan mit is jelent.

7 pontból 20 osztály van megjelölve c₁ (kék) az adatkészletben, ezért azt mondjuk p(c₁)=7/20. 7 pontunk van az osztályra c₂ (piros) is, ezért beállítjuk p(c₂)=7/20. Az utolsó osztály c₃ (sárga) csak 6 ponttal rendelkezik, tehát p(c₃)=6/20.

Az osztályvalószínűség ezen egyszerű számítása a maximális valószínűség megközelítéséhez hasonlít. Használhat azonban másikat is előzetes terjesztés, ha úgy tetszik. Például, ha tudja, hogy ez az adatkészlet nem reprezentálja a valódi sokaságot, mert osztály c₃ az esetek 50%-ában meg kell jelennie, akkor beállítja p(c₁)=0.25, p(c₂)=0.25 és p(c₃)=0.5. Bármi, ami segít a tesztkészlet teljesítményének javításában.

Most rátérünk a valószínűség p(x|c)=p(x₁, x₂|c). Ennek a valószínűségnek a kiszámításának egyik módja az adatkészlet szűrése a címkével ellátott mintákra c majd próbáljon meg olyan eloszlást találni (pl. 2-dimenziós Gauss), amely rögzíti a jellemzőket x₁, x₂.

Sajnos általában nincs elég mintánk osztályonként a valószínűség megfelelő becsléséhez.

Ahhoz, hogy robusztusabb modellt tudjunk építeni, elkészítjük a naiv feltételezés hogy a jellemzők x₁, x₂ faliórái sztochasztikusan független, adott c. Ez csak egy divatos módja annak, hogy megkönnyítse a matematikát

Kép a szerzőtől

minden osztály számára c. Itt van a naiv A naiv Bayes egy része abból származik, mert ez az egyenlet általában nem állja meg a helyét. Ennek ellenére a naiv Bayes még ekkor is jó, olykor kiemelkedő eredményeket hoz a gyakorlatban. Különösen az NLP-problémák esetében a zsák-szavas funkciókkal, a multinomiális naiv Bayes ragyog.

A fent megadott érvek ugyanazok minden naiv Bayes osztályozó esetében, amelyet talál. Most már csak attól függ, hogyan modellezed p(xXNUMX|cXNUMX), p(xXNUMX|cXNUMX), p(xXNUMX|cXNUMX), p(xXNUMX|c₂), p(xXNUMX|cXNUMX) és a p(x₂|c₃).

Ha a jellemzői csak 0 és 1, használhatja a Bernoulli eloszlás. Ha egész számok, a Multinomiális eloszlás. Azonban valódi jellemzőértékeink vannak, és a mellett döntünk Gauss eloszlása, innen ered a Gauss-naiv Bayes elnevezés. A következő formát vesszük fel

Kép a szerzőtől.

ahol μᵢ,ⱼ az átlagos és σᵢ,ⱼ az a szórás, amelyet meg kell becsülnünk az adatokból. Ez azt jelenti, hogy minden funkcióhoz egy átlagot kapunk i osztállyal párosulva cⱼ, esetünkben a 2*3=6 azt jelenti. Ugyanez vonatkozik a szórásokra is. Ez példát kíván.

Próbáljuk meg becsülni μ₂,₁ és a σ₂,₁. Mert j=1, minket csak az osztály érdekel c₁, csak ilyen címkével ellátott mintákat őrizzünk meg. A következő minták maradtak:

# samples with label = c_1 array([[ 0.14404357, 1.45427351], [ 0.97873798, 2.2408932 ], [ 1.86755799, -0.97727788], [ 1.76405235, 0.40015721], [ 0.76103773, 0.12167502], [-0.10321885, 0.4105985 ], [ 0.95008842, -0.15135721]])

Most, mert i=2 csak a második oszlopot kell figyelembe vennünk. μ₂,₁ az átlag és σ₂,₁ ennek az oszlopnak a szórása, azaz μ₂,₁ = 0.49985176 és σ₂,₁ = 0.9789976.

Ezeknek a számoknak van értelme, ha ismét felülről nézzük a szóródási diagramot. A jellemzői x₂ osztályból származó minták közül c₁ 0.5 körül vannak, ahogy a képen is látszik.

Ezt most kiszámoljuk a másik öt kombinációra, és kész is vagyunk!

Pythonban ezt a következőképpen teheti meg:

from sklearn.datasets import make_blobs
import numpy as np # Create the data. The classes are c_1=0, c_2=1 and c_3=2.
X, y = make_blobs( n_samples=20, centers=[(0, 0), (5, 5), (-5, 5)], random_state=0
) # The class probabilities.
# np.bincounts counts the occurence of each label.
prior = np.bincount(y) / len(y) # np.where(y==i) returns all indices where the y==i.
# This is the filtering step.
means = np.array([X[np.where(y == i)].mean(axis=0) for i in range(3)])
stds = np.array([X[np.where(y == i)].std(axis=0) for i in range(3)])

Kapunk

# priors
array([0.35, 0.35, 0.3 ])
# means array([[ 0.90889988, 0.49985176], [ 5.4111385 , 4.6491892 ], [-4.7841679 , 5.15385848]])
# stds
array([[0.6853714 , 0.9789976 ], [1.40218915, 0.67078568], [0.88192625, 1.12879666]])

Ez a Gauss-féle naiv Bayes-osztályozó képzésének eredménye.

Jóslatok készítése

A teljes előrejelzési képlet az

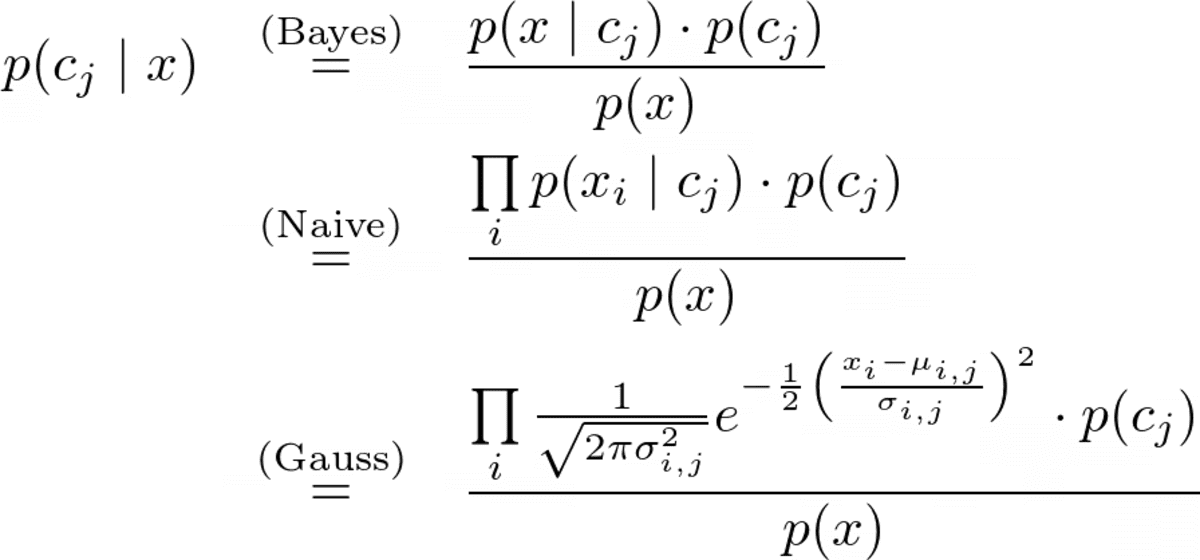
Kép a szerzőtől.

Tételezzünk fel egy új adatpontot x*=(-2, 5) jön be.

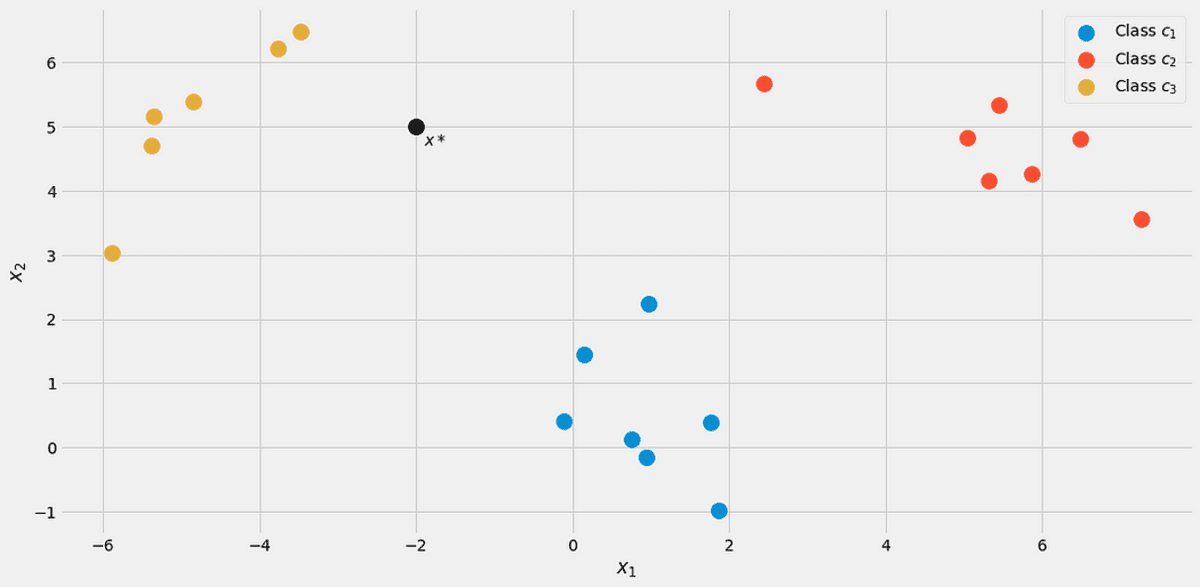
Kép a szerzőtől.

Számoljuk ki, hogy melyik osztályba tartozik p(c|x*) minden osztály számára. A kép alapján osztályba kell tartoznia c₃ = 2, de lássuk. Hagyjuk figyelmen kívül a nevezőt p(x) egy másodpercre. A következő ciklus segítségével kiszámították a nevezőket j = 1, 2, 3.

x_new = np.array([-2, 5]) for j in range(3): print( f"Probability for class {j}: {(1/np.sqrt(2*np.pi*stds[j]**2)*np.exp(-0.5*((x_new-means[j])/stds[j])**2)).prod()*p[j]:.12f}" )

Kapunk

Probability for class 0: 0.000000000263
Probability for class 1: 0.000000044359
Probability for class 2: 0.000325643718

Természetesen ezeket valószínűségek (nem szabad így neveznünk) ne adjunk egyet, mivel figyelmen kívül hagytuk a nevezőt. Ez azonban nem probléma, hiszen egyszerűen vehetjük ezeket a nem normalizált valószínűségeket, és eloszthatjuk az összegükkel, és akkor összeadunk egyet. Tehát ezt a három értéket elosztva körülbelül 0.00032569 összeggel, megkapjuk

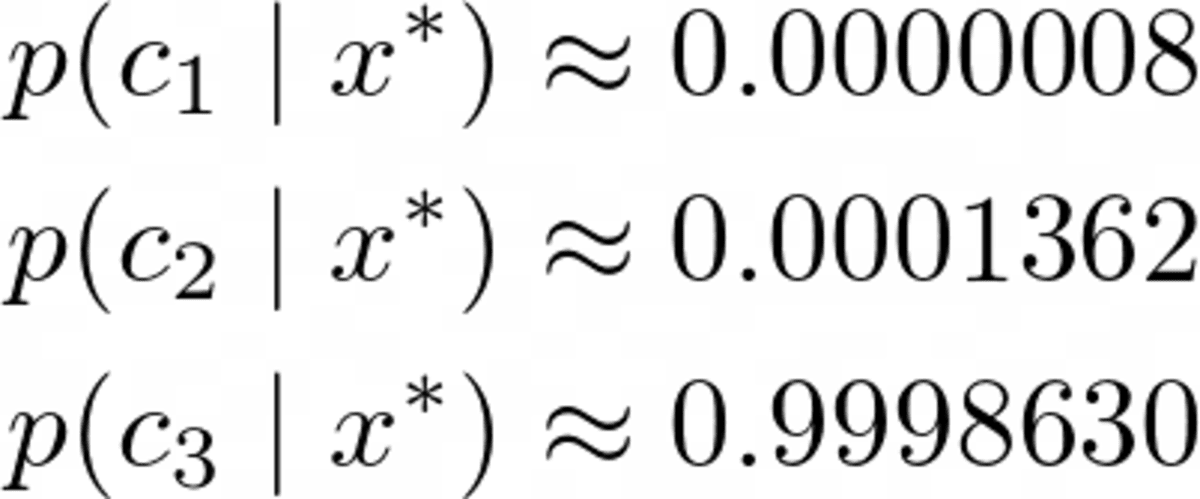
Kép a szerzőtől.

Egyértelmű győztes, ahogy vártuk. Most pedig hajtsuk végre!

Ez a megvalósítás messze nem hatékony, számszerűen nem stabil, csupán oktatási célt szolgál. A legtöbb dolgot megbeszéltük, így most könnyen követhetőnek kell lennie. Figyelmen kívül hagyhatja az összeset check funkciókat, vagy olvassa el a cikkemet Készítse el saját egyéni scikit-learnjét ha érdekel, mit csinálnak pontosan.

Csak vegye figyelembe, hogy megvalósítottam a predict_proba módszerrel először számítja ki a valószínűségeket. A módszer predict csak meghívja ezt a metódust, és az indexet (=osztályt) adja vissza a legnagyobb valószínűséggel egy argmax függvény segítségével (megint itt van!). Az osztály 0-tól várja az osztályokat k-1, hol k az osztályok száma.

import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted class GaussianNaiveBayesClassifier(BaseEstimator, ClassifierMixin): def fit(self, X, y): X, y = check_X_y(X, y) self.priors_ = np.bincount(y) / len(y) self.n_classes_ = np.max(y) + 1 self.means_ = np.array( [X[np.where(y == i)].mean(axis=0) for i in range(self.n_classes_)] ) self.stds_ = np.array( [X[np.where(y == i)].std(axis=0) for i in range(self.n_classes_)] ) return self def predict_proba(self, X): check_is_fitted(self) X = check_array(X) res = [] for i in range(len(X)): probas = [] for j in range(self.n_classes_): probas.append( ( 1 / np.sqrt(2 * np.pi * self.stds_[j] ** 2) * np.exp(-0.5 * ((X[i] - self.means_[j]) / self.stds_[j]) ** 2) ).prod() * self.priors_[j] ) probas = np.array(probas) res.append(probas / probas.sum()) return np.array(res) def predict(self, X): check_is_fitted(self) X = check_array(X) res = self.predict_proba(X) return res.argmax(axis=1)

A megvalósítás tesztelése

Bár a kód meglehetősen rövid, még mindig túl hosszú ahhoz, hogy teljesen biztosak lehessünk abban, hogy nem követtünk el hibát. Tehát nézzük meg, hogyan viszonyul a scikit-learn GaussianNB osztályozó.

my_gauss = GaussianNaiveBayesClassifier()
my_gauss.fit(X, y)
my_gauss.predict_proba([[-2, 5], [0,0], [6, -0.3]])

kimenetek

array([[8.06313823e-07, 1.36201957e-04, 9.99862992e-01], [1.00000000e+00, 4.23258691e-14, 1.92051255e-11], [4.30879705e-01, 5.69120295e-01, 9.66618838e-27]])

Az előrejelzések segítségével a predict módszer azok

# my_gauss.predict([[-2, 5], [0,0], [6, -0.3]])
array([2, 0, 1])

Most pedig használjuk a scikit-learnt. Valami kód bedobása

from sklearn.naive_bayes import GaussianNB gnb = GaussianNB()
gnb.fit(X, y)
gnb.predict_proba([[-2, 5], [0,0], [6, -0.3]])

hozamok

array([[8.06314158e-07, 1.36201959e-04, 9.99862992e-01], [1.00000000e+00, 4.23259111e-14, 1.92051343e-11], [4.30879698e-01, 5.69120302e-01, 9.66619630e-27]])

A számok hasonlítanak a mi osztályozónk számaihoz, de kissé eltérnek az utolsó néhány számjegytől. Csináltunk valami rosszat? Nem. A scikit-learn verzió csupán egy másik hiperparamétert használ var_smoothing=1e-09 . Ha ezt úgy állítjuk be nulla, pontosan megkapjuk a számainkat. Tökéletes!

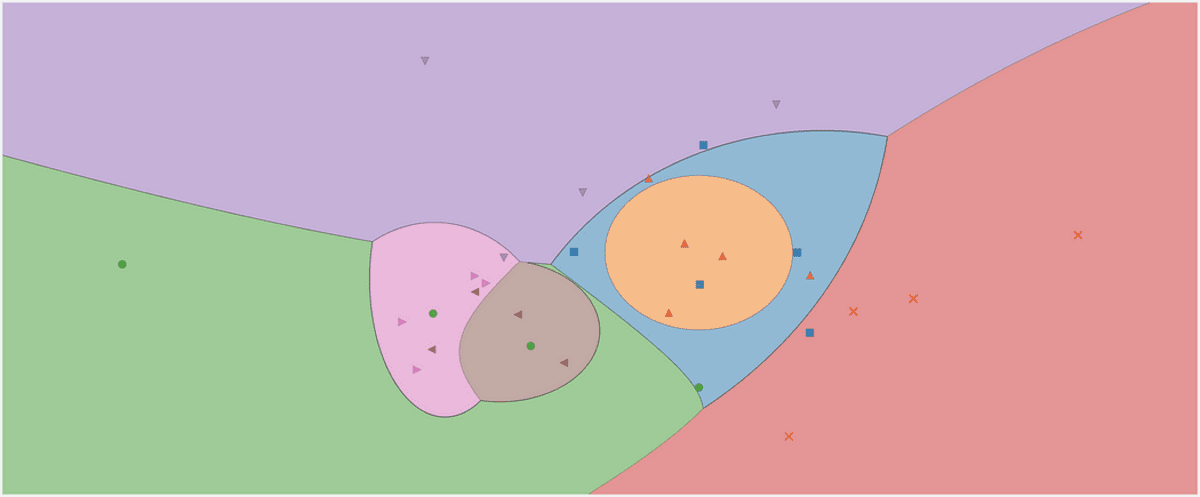
Tekintse meg osztályozónk döntési régióit. A teszteléshez használt három pontot is bejelöltem. A határhoz közeli pontnak csak 56.9% az esélye, hogy a vörös osztályba tartozzon, amint az a predict_proba kimenetek. A másik két pont sokkal nagyobb biztonsággal van besorolva.

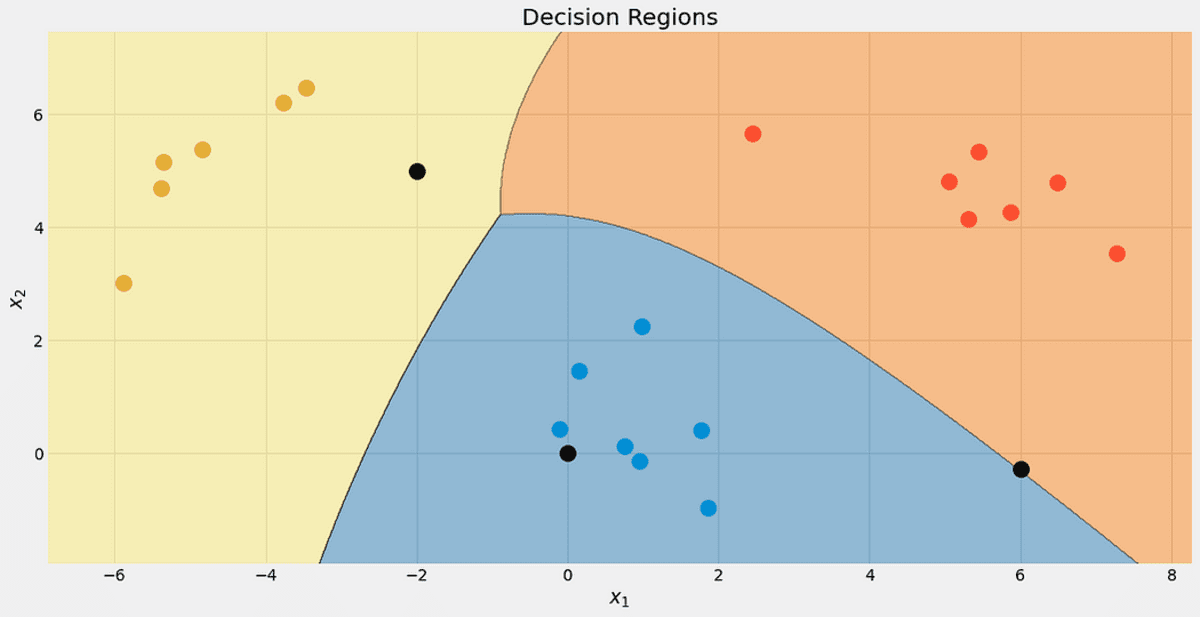
A döntési régiók a 3 új ponttal. Kép a szerzőtől.

Ebben a cikkben megtudtuk, hogyan működik a Gauss-féle naiv Bayes-osztályozó, és megérzést adtunk arról, hogy miért így tervezték – ez egy közvetlen megközelítés az érdeklődési valószínűség modellezésére. Hasonlítsa össze ezt a logisztikus regresszióval: ott a valószínűséget egy lineáris függvénnyel modellezik, amelyre szigmoid függvényt alkalmaznak. Még mindig könnyű modell, de nem olyan természetes, mint egy naiv Bayes osztályozó.

Néhány példa kiszámításával folytattuk, és útközben összegyűjtöttünk néhány hasznos kódrészletet. Végül megvalósítottunk egy teljes Gauss-féle naiv Bayes osztályozót oly módon, amely jól működik a scikit-learn-nel. Ez azt jelenti, hogy használhatja például csővezetékekben vagy rácskeresésben.

Végül elvégeztünk egy kis józansági ellenőrzést: importáltuk a scikit-learns saját Gauss-féle naiv Bayes osztályozóját, és megvizsgáltuk, hogy a mi és a scikit-learn osztályozója ugyanazt az eredményt adja-e. Ez a teszt sikeres volt.

 
 
Dr. Kübler Róbert a Publicis Media adattudósa és a Towards Data Science szerzője.

 
eredeti. Engedéllyel újra közzétéve.
 

• SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
• Platoblockchain. Web3 metaverzum intelligencia. Felerősített tudás. Hozzáférés itt.
• Forrás: https://www.kdnuggets.com/2023/03/gaussian-naive-bayes-explained.html?utm_source=rss&utm_medium=rss&utm_campaign=gaussian-naive-bayes-explained