[Peili] Toisen asteen aritmeettiset ohjelmat: nollasta sankariin

Vitalik Buterin kautta Vitalik Buterin blogi

Tämä on peili postista osoitteessa https://medium.com/@VitalikButerin/quadratic-aritmetic-programs-from-zero-to-hero-f6d558cea649

Viime aikoina on ollut paljon kiinnostusta zk-SNARKien takana olevaa tekniikkaa kohtaan, ja ihmiset ovat yhä enemmän yrittää demystifioida jotain, jota monet ovat alkaneet kutsua "kuun matematiikaksi" sen kokeman tulkitsemattoman monimutkaisuuden vuoksi. zk-SNARKit ovat todellakin melko haastavia tarttua, varsinkin johtuen valtavasta määrästä liikkuvia osia, joiden on yhdistettävä, jotta kokonaisuus toimisi, mutta jos hajotamme teknologian pala palalta, sen ymmärtäminen on yksinkertaisempaa.

Tämän viestin tarkoituksena ei ole toimia täydellisenä johdannona zk-SNARKeihin; se olettaa taustatiedoksi, että (i) tiedät mitä zk-SNARKit ovat ja mitä ne tekevät, ja (ii) tiedät tarpeeksi matematiikkaa voidaksesi perustella asioita, kuten polynomeja (jos lause �(�)+�(�) =(�+�)(�) , jossa � ja � ovat polynomeja, näyttää sinulle luonnolliselta ja itsestään selvältä, niin olet oikealla tasolla). Pikemminkin viesti kaivaa syvemmälle tekniikan takana olevaa koneistoa ja yrittää selittää mahdollisimman hyvin putkilinjan ensimmäisen puoliskon, kuten zk-SNARK-tutkija Eran Tromer on piirtänyt tähän:

Tässä olevat vaiheet voidaan jakaa kahteen osaan. Ensinnäkin zk-SNARK:ia ei voida soveltaa suoraan mihinkään laskennalliseen ongelmaan; pikemminkin sinun on muutettava ongelma oikeaan "muotoon", jotta ongelma voi toimia. Muotoa kutsutaan "neliöaritmeettiseksi ohjelmaksi" (QAP), ja funktion koodin muuntaminen yhdeksi näistä on itsessään erittäin epätriviaali. Toiminnon koodin QAP:ksi muuntamisen rinnalla on toinen prosessi, jota voidaan ajaa rinnakkain niin, että jos sinulla on syöte koodiin, voit luoda vastaavan ratkaisun (jota kutsutaan joskus QAP:n "todistajiksi"). Tämän jälkeen on toinen melko monimutkainen prosessi todellisen "nollatiedon todisteen" luomiseksi tälle todistajalle ja erillinen prosessi todisteiden tarkistamiseksi, että joku muu välittää sinulle, mutta nämä ovat yksityiskohtia, jotka eivät kuulu tähän viestiin. .

Valitsemme yksinkertaisen esimerkin: todistaa, että tiedät kuutioyhtälön ratkaisun: �3+�+5=35 (vinkki: vastaus on 3). Tämä ongelma on riittävän yksinkertainen, jotta tuloksena oleva QAP ei ole niin suuri, että se olisi pelottava, mutta tarpeeksi epätriviaali, jotta voit nähdä kaiken koneiston tulevan peliin.

Kirjoitetaan funktiomme seuraavasti:

def qeval(x):
    y = x**3
    return x + y + 5

Tässä käyttämämme yksinkertainen erikoisohjelmointikieli tukee perusaritmetiikkaa (+, −, ⋅, /), vakiotehoista eksponentiota (�7, mutta ei ��) ja muuttujien osoitusta, joka on tarpeeksi tehokas, jotta voit tehdä sen teoreettisesti. mikä tahansa laskenta sen sisällä (kunhan laskentavaiheiden määrä on rajoitettu; silmukoita ei sallita). Huomaa, että modulo (%) ja vertailuoperaattoreita (<, >, ≤, ≥) EI tueta, koska ei ole tehokasta tapaa tehdä moduloa tai vertailua suoraan äärellisen syklisen ryhmän aritmetiikassa (ole kiitollinen tästä, jos sellainen oli mahdollista). jos haluat tehdä jommankumman, elliptisen käyrän salaus murtuisi nopeammin kuin voit sanoa "binäärihaku" ja "kiinalainen jäännöslause").

Voit laajentaa kielen moduloon ja vertailuihin antamalla bittihajotelmia (esim. 13=23+22+1) aputuloina, todistamalla näiden hajottelujen oikeellisuuden ja laskemalla binääripiirejä; äärellisen kentän aritmetiikassa yhtäläisyyden (==) tarkistusten tekeminen on myös mahdollista ja itse asiassa hieman helpompaa, mutta nämä ovat molemmat yksityiskohtia, joihin emme nyt mene. Voimme laajentaa kieltä tukemaan ehdollisia lausekkeita (esim. jos �<5:�=7; else: �=9) muuntamalla ne aritmeettiseen muotoon: �=7⋅(�<5)+9⋅(�≥5 ), mutta huomaa, että ehdollisen ehdon molemmat "polut" on suoritettava, ja jos sinulla on useita sisäkkäisiä ehtoja, tämä voi johtaa suureen määrään lisäkustannuksia.

Käydään nyt tämä prosessi läpi vaihe vaiheelta. Jos haluat tehdä tämän itse jollekin koodille, I otti käyttöön kääntäjän täällä (vain koulutustarkoituksiin; ei ole vielä valmis QAP:ien tekemiseen todellisille zk-SNARKeille!).

litistyminen

Ensimmäinen vaihe on litistysmenettely, jossa muunnetaan alkuperäinen koodi, joka voi sisältää mielivaltaisen monimutkaisia ​​lauseita ja lausekkeita, lausesarjaksi, jolla on kaksi muotoa: �=� (jossa � voi olla muuttuja tai luku ) ja �=� (��) � (jossa �� voi olla +, −, ⋅, / ja � ja � voivat olla muuttujia, numeroita tai itse alilausekkeita). Voit ajatella jokaista näistä lauseista tavallaan kuin logiikkaportteja piirissä. Yllä olevan koodin tasoitusprosessin tulos on seuraava:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

Jos luet alkuperäisen koodin ja koodin täältä, voit melko helposti nähdä, että nämä kaksi ovat samanarvoisia.

Portit R1CS:ään

Nyt muunnetaan tämä joksikin, jota kutsutaan rank-1 rajoitusjärjestelmäksi (R1CS). R1CS on kolmen vektorin (�, �, �) ryhmien sarja, ja R1CS:n ratkaisu on vektori �, jossa �n on täytettävä yhtälö �.�⋅�.�−�.�=0, missä . edustaa pistetuloa – yksinkertaisemmin sanottuna, jos "vetoilemme yhteen" � ja � kertomalla nämä kaksi arvoa samoissa kohdissa ja sitten laskemme näiden tulojen summan, teemme sitten samoin � ja � ja sitten � ja � , niin kolmas tulos on yhtä suuri kuin kahden ensimmäisen tuloksen tulo. Esimerkiksi tämä on tyytyväinen R1CS:

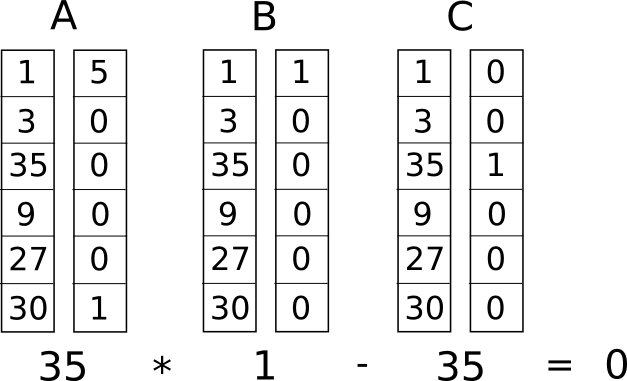
Mutta sen sijaan, että meillä olisi vain yksi rajoitus, meillä on monia rajoituksia: yksi jokaiselle logiikkaportille. On olemassa standardi tapa muuntaa logiikkaportti (�,�,�) kolmiosaiseksi riippuen siitä, mikä operaatio on (+, −, ⋅ tai /) ja ovatko argumentit muuttujia vai numeroita. Kunkin vektorin pituus on yhtä suuri kuin järjestelmän muuttujien kokonaismäärä, mukaan lukien valemuuttuja ~ yksi ensimmäisessä indeksissä, joka edustaa numeroa 1, tulomuuttujat, valemuuttuja ~ out, joka edustaa lähtöä, ja sitten kaikki välimuuttujat (���1 ja ���2 edellä); vektorit ovat yleensä hyvin harvassa, täyttäen vain aikavälit, jotka vastaavat muuttujia, joihin jokin tietty logiikkaportti vaikuttaa.

Ensin tarjoamme käyttämämme muuttujakartoituksen:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

Ratkaisuvektori koostuu kaikkien näiden muuttujien tehtävistä tässä järjestyksessä.

Nyt annamme (�,�,�) kolminkertaisen ensimmäisen portin:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

Voit nähdä, että jos ratkaisuvektori sisältää 3 toisessa paikassa ja 9 neljännessä asemassa, niin ratkaisuvektorin muusta sisällöstä riippumatta pistetulon tarkistus tiivistyy arvoon 3⋅3=9, ja niin se menee ohi. Jos ratkaisuvektorin toisessa paikassa on −3 ja neljännessä paikassa 9, myös tarkistus menee läpi; itse asiassa, jos ratkaisuvektorin toisessa paikassa on 7 ja neljännessä paikassa 49, tämä tarkistus silti läpäisee - tämän ensimmäisen tarkistuksen tarkoituksena on varmistaa vain ensimmäisen portin tulojen ja lähtöjen johdonmukaisuus.

Jatketaan nyt toiseen porttiin:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

Samalla tavalla kuin ensimmäisen pisteen tuotetarkistuksessa, tarkistamme tässä, että ���1⋅�=�.

Nyt kolmas portti:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

Tässä kuvio on hieman erilainen: ratkaisuvektorin ensimmäinen elementti kerrotaan toisella elementillä, sitten viidennellä elementillä, lasketaan yhteen kaksi tulosta ja tarkistetaan, onko summa yhtä suuri kuin kuudes alkio. Koska ratkaisuvektorin ensimmäinen elementti on aina yksi, tämä on vain yhteenlaskutarkistus, jolla tarkistetaan, että tulos on yhtä suuri kuin kahden syötteen summa.

Lopuksi neljäs portti:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

Tässä arvioimme viimeistä sekkiä, ~out =���2+5. Pistetulon tarkistus toimii ottamalla ratkaisuvektorin kuudes elementti, lisäämällä viisi kertaa ensimmäinen elementti (muistutus: ensimmäinen elementti on 1, joten tämä tarkoittaa käytännössä 5:n lisäämistä) ja vertaamalla sitä kolmanteen elementtiin, jossa me tallentaa lähtömuuttujan.

Ja siellä meillä on R1CS neljällä rajoituksella. Todistaja on yksinkertaisesti määritys kaikille muuttujille, mukaan lukien tulo-, lähtö- ja sisäiset muuttujat:

[1, 3, 35, 9, 27, 30]

Voit laskea tämän itse "suorittamalla" yllä olevan litteän koodin, aloittamalla syötemuuttujien määrityksellä �=3 ja lisäämällä kaikkien välimuuttujien arvot ja tulosteen niitä laskeessasi.

Täydellinen R1CS koottu on:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS QAP:iin

Seuraava askel on ottaa tämä R1CS ja muuntaa se QAP-muotoon, joka toteuttaa täsmälleen saman logiikan paitsi käyttämällä polynomeja pistetulojen sijaan. Teemme tämän seuraavasti. Menemme 3 neljästä kolmen pituisen kuusi vektorin ryhmästä kuuteen kolmen asteen 3 polynomin ryhmään, jossa arvioidaan kunkin polynomin x koordinaatti edustaa yhtä rajoituksista. Eli jos arvioimme polynomit kohdassa �=1, saamme ensimmäisen vektorijoukon, jos arvioimme polynomit kohdassa �=2, niin saamme toisen vektorijoukon ja niin edelleen.

Voimme tehdä tämän muunnoksen käyttämällä jotain nimeltä a Lagrangen interpolointi. Ongelma, jonka Lagrangen interpolaatio ratkaisee, on tämä: jos sinulla on joukko pisteitä (eli (�,�) koordinaattipareja), Lagrangen interpolointi näissä pisteissä antaa sinulle polynomin, joka kulkee kaikkien näiden pisteiden läpi. Teemme tämän hajottamalla tehtävän: luomme jokaiselle koordinaatille polynomin, jolla on haluttu koordinaatti kyseisessä koordinaatissa ja koordinaatti 0 kaikissa muissa meitä kiinnostavissa koordinaateissa, ja sitten saadaan lopullinen. tuloksena laskemme kaikki polynomit yhteen.

Tehdään esimerkki. Oletetaan, että haluamme polynomin, joka kulkee (1,3), (2,2) ja (3,4) läpi. Aloitamme tekemällä polynomin, joka kulkee (1,3), (2,0) ja (3,0) läpi. Kuten käy ilmi, sellaisen polynomin tekeminen, joka "jäänyt esiin" kohdassa �=1 ja on nolla muissa kiinnostavissa kohdissa, on helppoa; teemme yksinkertaisesti:

(x - 2) * (x - 3)

Joka näyttää tältä:

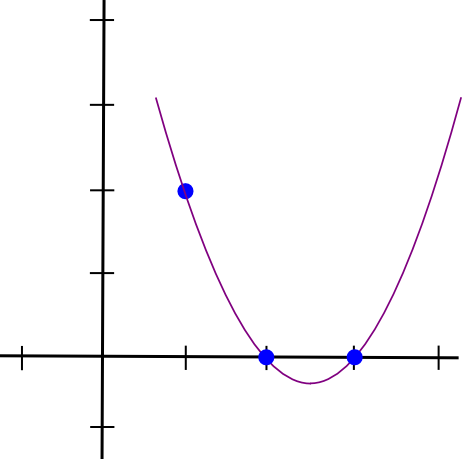
Nyt meidän on vain "skaalattava" se niin, että korkeus kohdassa x = 1 on oikea:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

Tämä antaa meille:

1.5 * x**2 - 7.5 * x + 9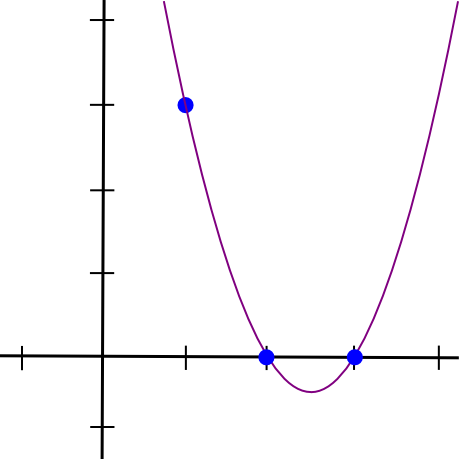

Teemme sitten saman kahdella muulla pisteellä ja saamme kaksi muuta samannäköistä polynomia, paitsi että ne "jäävät ulos" kohdissa �=2 ja �=3 �=1:n sijaan. Lisäämme kaikki kolme yhteen ja saamme:

1.5 * x**2 - 5.5 * x + 7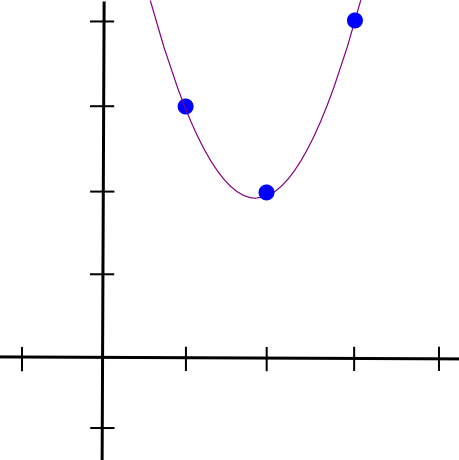

Juuri sellaisilla koordinaatilla kuin haluamme. Yllä kuvattu algoritmi vie �(�3) aikaa, koska pisteitä on � ja jokainen piste vaatii �(�2) aikaa kertoakseen polynomit yhteen; pienellä ajattelulla tämä voidaan lyhentää �(�2) aikaan, ja paljon enemmän ajattelua käyttämällä nopeita Fourier-muunnosalgoritmeja ja vastaavia, sitä voidaan vähentää entisestään – ratkaiseva optimointi, kun funktiot, jotka tottuvat zk:hen -SNARKeissa on käytännössä usein useita tuhansia portteja.

Käytetään nyt Lagrangen interpolaatiota R1CS:n muuntamiseen. Otamme ensimmäisen arvon jokaisesta vektorista, teemme siitä polynomin Lagrangen interpoloinnilla (jos polynomin arvioiminen kohdassa � saa ensimmäisen arvon �:nnelle � vektorille), toista prosessi. jokaisen �- ja �-vektorin ensimmäiselle arvolle ja toista sitten tämä prosessi toisille arvoille, kolmannelle arvoille ja niin edelleen. Mukavuuden vuoksi annan vastaukset heti:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

Kertoimet ovat nousevassa järjestyksessä, joten ensimmäinen polynomi yllä on itse asiassa 0.833⋅�3—5⋅�2+9.166⋅�−5. Tämä polynomijoukko (sekä Z-polynomi, jonka selitän myöhemmin) muodostaa tämän tietyn QAP-esiintymän parametrit. Huomaa, että kaikki työ tähän pisteeseen asti on tehtävä vain kerran jokaista toimintoa kohden, jonka yrität käyttää zk-SNARKeja vahvistamaan; Kun QAP-parametrit on luotu, niitä voidaan käyttää uudelleen.

Yritetään arvioida kaikki nämä polynomit arvolla �=1. Polynomin arvioiminen arvolla �=1 tarkoittaa yksinkertaisesti kaikkien kertoimien laskemista yhteen (kuten 1�=1 kaikille �), joten se ei ole vaikeaa. Saamme:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

Ja katso ja katso, se, mitä meillä on täällä, on täsmälleen sama kuin kolmen vektorin joukko ensimmäiselle logiikkaportille, jonka loimme edellä.

QAP:n tarkistus

Mitä järkeä tässä hullussa muutoksessa nyt on? Vastaus on, että sen sijaan, että tarkistamme R1CS:n rajoitukset erikseen, voimme nyt tarkistaa kaikki rajoitukset samaan aikaan tekemällä pisteen tuotetarkistus polynomeilla.

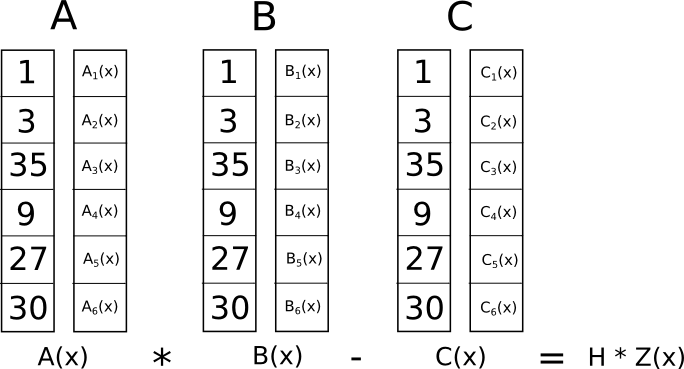
Koska tässä tapauksessa pistetulon tarkistus on sarja polynomien yhteen- ja kertolaskuja, tuloksesta tulee itse polynomi. Jos tuloksena oleva polynomi, joka on arvioitu jokaisella koordinaatilla, jota käytimme yllä edustamaan logiikkaporttia, on yhtä suuri kuin nolla, se tarkoittaa, että kaikki tarkistukset läpäisevät; jos tuloksena oleva polynomi, joka on arvioitu vähintään yhdessä logiikkaporttia edustavista �-koordinaateista, antaa nollasta poikkeavan arvon, se tarkoittaa, että kyseiseen loogiseen porttiin menevät ja sieltä lähtevät arvot ovat epäjohdonmukaisia ​​(eli portti on �=�⋅�� �1, mutta annetut arvot voivat olla �=2,���1=2 ja �=5).

Huomaa, että tuloksena olevan polynomin ei itse tarvitse olla nolla, eikä itse asiassa useimmissa tapauksissa olekaan; sillä voi olla mitä tahansa käyttäytymistä pisteissä, jotka eivät vastaa mitään logiikkaportteja, kunhan tulos on nolla kaikissa pisteissä, jotka do vastaa jotain porttia. Oikeuden tarkistamiseksi emme itse asiassa arvioi polynomia �=�.�⋅�.�−�.� jokaisessa porttia vastaavassa pisteessä; sen sijaan jaamme � toisella polynomilla � ja tarkistamme, että � jakaa tasaisesti � – eli jako �/� ei jätä jäännöstä.

� määritellään seuraavasti: (�−1)⋅(�−2)⋅(�−3)… – yksinkertaisin polynomi, joka on yhtä suuri kuin nolla kaikissa logiikkaportteja vastaavissa pisteissä. Se on algebran alkeellinen tosiasia Kaikki polynomin, joka on nolla kaikissa näissä pisteissä, on oltava tämän minimipolynomin kerrannainen, ja jos polynomi on �:n kerrannainen, sen arvio missä tahansa näistä pisteistä on nolla; tämä vastaavuus tekee työstämme paljon helpompaa.

Tehdään nyt itse asiassa pistetulon tarkistus yllä olevilla polynomeilla. Ensin välipolynomit:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

Nyt �.�⋅�.�—�.�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

Nyt minimipolynomi �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):

Z = [24, -50, 35, -10, 1]

Ja jos jaamme yllä olevan tuloksen �:lla, saamme:

h = t / Z = [-3.666, 17.055, -3.444]

Ilman jäännöstä.

Ja niin meillä on ratkaisu QAP:lle. Jos yritämme väärentää mitä tahansa muuttujaa R1CS-ratkaisussa, josta johdamme tämän QAP-ratkaisun - esimerkiksi asetamme viimeiseksi 31:ksi 30:n sijaan, niin saamme �-polynomin, joka epäonnistuu yhdessä tarkistuksista (tässä nimenomaisessa tapauksessa �=3:n tulos olisi −1 arvon 0 sijasta), eikä � olisi lisäksi luvun � kerrannainen; pikemminkin jakamalla �/� jäännökseen [−5.0,8.833,−4.5,0.666].

Huomaa, että yllä oleva on yksinkertaistus; "todellisessa maailmassa" yhteen-, kerto-, vähennys- ja jakolasku ei tapahdu säännöllisillä luvuilla, vaan äärellisillä kenttäelementeillä - pelottava aritmetiikka, joka on itsestään johdonmukainen, joten kaikki tuntemamme ja rakastamamme algebralliset lait ovat edelleen pitää paikkansa, mutta jossa kaikki vastaukset ovat jonkin äärellisen joukon elementtejä, yleensä kokonaislukuja välillä 0 - �−1 joillekin �ille. Jos esimerkiksi �=13, niin 1/2=7 (ja 7⋅2=1),3⋅5=2 ja niin edelleen. Äärillisen kentän aritmetiikka poistaa tarpeen huolehtia pyöristysvirheistä ja antaa järjestelmän toimia hienosti elliptisten käyrien kanssa, jotka lopulta ovat välttämättömiä muulle zk-SNARK-koneistolle, mikä tekee zk-SNARK-protokollasta todella turvallisen.

Erityiskiitokset Eran Tromerille, joka auttoi selittämään minulle monia yksityiskohtia zk-SNARKien sisäisestä toiminnasta.

• SEO-pohjainen sisällön ja PR-jakelu. Vahvista jo tänään.
• PlatoData.Network Vertical Generatiivinen Ai. Vahvista itseäsi. Pääsy tästä.
• PlatoAiStream. Web3 Intelligence. Tietoa laajennettu. Pääsy tästä.
• PlatoESG. hiili, CleanTech, energia, ympäristö, Aurinko, Jätehuolto. Pääsy tästä.
• PlatonHealth. Biotekniikan ja kliinisten kokeiden älykkyys. Pääsy tästä.
• BlockOffsets. Ympäristövastuun omistuksen nykyaikaistaminen. Pääsy tästä.
• Lähde: Platon Data Intelligence.