基于人工智能的数独解决方案

基于人工智能的数独解决方案

时间戳记：29年2024月9日，凌晨40:XNUMX
源节点： 3091242

29 月 XNUMX 日是国家拼图日，为了庆祝，我们创建了一个有趣的博客，详细介绍了如何使用人工智能 (AI) 解决数独。

介绍

之前 Wordle的是， 数独谜题 曾经风靡一时，现在仍然很受欢迎。近年来，利用 优化 解决难题的方法一直是一个主导主题。看 “在 Arkieva 中使用优化解决数独难题“。

当前，人工智能的使用主要集中在机器学习上，其中包含从套索回归到强化学习等多种方法。人工智能的使用已经 重新出现 来应对复杂的 调度 挑战。一种常用的方法是回溯搜索，并且非常适合数独。

本博客将详细介绍如何使用此方法来解决数独问题。事实证明，“回溯”可以在优化和机器学习引擎中找到，并且是 Arkieva 用于调度的高级启发式算法的基石。该算法是用“数组编程语言”实现的，这是一种面向函数的编程语言，可以处理 丰富的数组结构.

数独基础知识

从维基百科：数独是一种基于逻辑的组合数字放置谜题。目标是用数字填充 9×9 网格，以便构成网格的每一列、每一行以及 3 个 3×1 子网格（也称为“框”、“块”、“区域”）或“子方格”）包含从 9 到 9 的所有数字。拼图设置器提供部分完成的网格，该网格通常具有唯一的解决方案。已完成的谜题始终是一种拉丁方，对各个区域的内容有额外的限制。例如，相同的单个整数不能在相同的9×3游戏板行或列中或在3×9游戏板的九个9×XNUMX子区域中的任何一个中出现两次。

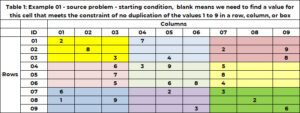
表 1 有一个示例问题。有 9 行 9 列，总共 81 个单元格。每个单元格只能有 1 到 9 之间的九个整数中的一个。在起始解决方案中，单元格要么有一个值 - 将此单元格中的值固定为该值，要么单元格为空白，表明我们需要找到该单元格的值。单元格 (1,1) 的值为 2，单元格 (6,5) 的值为 6。单元格 (1,2) 和单元格 (2,3) 为空白，算法将为这些单元格找到一个值。

并发症

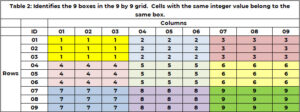
一个单元格除了属于一个且仅一行和一列之外，还属于一个且仅1个框。有 9 个框，在表 1 中用颜色表示。表 2 使用 1 到 9 之间的唯一整数来标识每个框或网格。行值为 (1, 2 或 3) 列值为 (1, 2 或 3) 的单元格属于框 1。框 6 为行值为 (4, 5, 6) 列值为 (7, 8) ，9）。盒子 id 由公式 BOX_ID = {3x(floor((ROW_ID-1) /3)} + upper (COL_ID/3) 确定。对于单元格 (5,7)，6 = 3x(floor(5-1) ))/3) + 上限 (8/3)= 3×1 + 3 = 3+3。

谜题的核心

为每个未知单元格找到一个介于 1 和 9 之间的整数值，使得整数 1 到 9 对于每一列、每一行和每个框仅使用一次。

让我们看看单元格 (1,3)，它是空白的。第 1 行已具有值 2 和 7。此单元格中不允许使用这些值。第 3 列已有值 3、5,6、7,9、1、2。这些都是不允许的。框 3（黄色）的值为 8、2,7 和 3。这些是不允许的。不允许使用以下值 (5)； （6、7、9、2、3）； (8)。不允许的唯一值是 (2, 3, 5, 6, 7, 8, 9)。唯一的候选值是 (1,4)。

一种解决方法是暂时将 1 分配给单元格 (1,3)，然后尝试查找另一个单元格的候选值。

回溯解决方案：启动组件

数组结构

首先是决定一个数组结构来存储源问题并支持搜索。表 3 就是这个数组结构。第 1 列是每个单元格的唯一整数 ID。值范围从 1 到 81。第 2 列是单元格的行 ID。第 3 列是单元格的列 ID。第 4 列是盒子 ID。第 5 列是单元格中的值。观察没有值的单元格被赋予值零而不是空白或空。这使其成为“仅限整数的数组”——性能远超优越。

在 APL 中，该数组将存储在形状为 2 x 81 的二维数组中。假设表 5 的元素存储在变量 MAT 中。示例函数有：

命令 MAT[1 2 3;] 获取 MAT 的前 3 行
1 1 1 1 2
2 1 2 1 0
3 1 3 1 0
垫[1 2 3; 4 5] 保护第 1、2、3 行以及仅第 4 和 5 列
1 2
1 0
1 0
(MAT[;5]=0)/MAT[;1] 查找所有需要值的单元格。

插入表3

健全性检查：重复

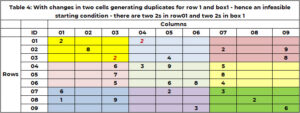
在开始搜索之前，进行健全性检查至关重要！这是可行的起始解决方案。对于数独来说可行的是，现在任何行、列或框中都有重复项。当前的起始方案例如1是可行的。表 4 提供了一个示例，其中起始解决方案具有重复项。第 1 行有两个值 2。区域 1 有两个值 2。函数“SANITY_DUPE”处理此逻辑。

健全性检查：没有值的单元格的选项

一条非常有用的信息是没有值的单元格的所有可能值。如果没有候选人，那么这个难题就无法解决。一个单元不能采用其邻居已经声明的值。使用表 1 中的单元格 (1,3,'1' – 最后一个 1 是 boxid)，它的邻居是行 1、列 3 和框 1。行 1 的值为 (2,7)；行 3 的值为 (3,5,6,7,9)；第 1 列的值为 (2,3,8)；框 1,3.1 的值为 (2,3,5,6,7,8,9)。单元格 (1,3,1) 不能采用以下值 (1,4)。单元格 (4,1,2) 的唯一选项是 (1)。对于单元格 (2)，值 3、5、6、7、9、4、1 已在第 4 行、第 4,8 列和/或第 XNUMX 框中使用。唯一的候选值是 (XNUMX) 。函数“SANITY_CAND”处理此逻辑。

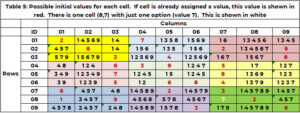
表 5 显示了候选者，例如搜索过程开始时的 1。如果单元格已在起始条件（表 1）中分配了值，则该值将重复并显示为红色。如果需要值的单元格只有一个选项，则该选项显示为白色。单元格 (8,7,9) 的单个值 7 为白色。 (2,5,8,4,3) 由相邻列 7 声明。(1) 由第 2 行声明。(9) 由框 8 声明。只有值 3,2,6 未被声明。

健全性检查：寻找冲突

识别需要值的单元格的所有选项的信息（表 4 中发布）使我们能够在开始搜索过程之前识别冲突。当两个需要某个值的单元格只有一个候选值、候选值相同并且这两个单元格是邻居时，就会发生冲突。从表 4 中我们知道唯一需要值并且只有一个候选值的单元格是单元格 (8,7,9)。例如1，不存在冲突。

会发生什么冲突？如果单元格 (3,7,3) 的唯一可能值为 7（而不是 1），则存在冲突。单元格 (6) 和单元格 (7) 是邻居——同一列。但是，如果单元格 (8,7) 的唯一可能值是 3,7（而不是 4,9,2），则这不会产生冲突。这些细胞不是邻居。

健全性检查摘要

  1. 如果存在重复项，则起始解决方案不可行。
  2. 如果一个需要值的单元格没有任何候选值，那么这个难题就没有可能的解决方案。每个单元格的候选值列表可用于减少搜索空间 - 用于回溯和优化。
  3. 发现冲突的能力表明，如果没有搜索过程，这个难题是不可行的——没有解决方案。此外，它还能识别“问题细胞”。

回溯解决方案：搜索过程

核心数据结构和健全性检查到位后，我们将注意力转向搜索过程。反复出现的主题是，建立适当的数据结构来支持搜索。

追踪搜索

数组 跟踪 跟踪所做的作业

  1. 第 1 列是计数器
  2. 第 2 列是可分配给该单元格的选项数量
    • 1 表示有 1 个选项可用，2 表示有两个选项，依此类推。
    • 0 表示 – 无可用选项或重置为 0（未分配值）并回溯
  3. 第 3 列是分配有值索引号的单元格（1 到 81）
  4. 第 4 列是分配给轨迹历史记录中单元格的值
    • 值 9999 表示发现死胡同时就是该单元格
    • 1 到 9 之间的整数值是搜索过程中此时分配给该单元格的值。
    • 值为 0 表示该单元格需要分配

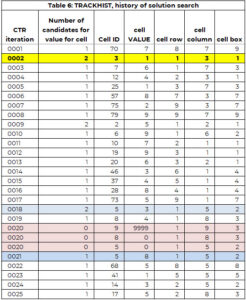
跟踪器阵列用于支持搜索过程。数组 轨迹记录 与跟踪器具有相同的结构，但保留整个搜索过程的历史记录。表 6 包含示例 1 的 TRACKHIST 的一部分。在后面的部分中将对其进行更详细的解释。

另外，数组 PAV （向量的向量），跟踪先前分配给该单元格的值。这确保我们不会重新审视失败的解决方案——类似于 TABU 中所做的事情。

有一个可选的日志进程，搜索进程会在其中写出每个步骤。

开始搜索

完成簿记和健全性检查后，我们现在可以开始搜索过程。步骤是：

  1. 是否还有需要值的单元格？ – 如果没有，那么我们就完成了。
  2. 对于每个需要值的单元格，找到每个单元格的所有候选选项。表 4 列出了求解过程开始时的这些值。在每次迭代中，都会更新它以适应分配给单元格的值。
  3. 按此顺序评估选项。
    • 如果一个单元格有零个选项，则进行回溯
    • 查找具有一个选项的所有单元格，选择这些单元格之一，进行此分配，
      1. 并更新跟踪表、当前解决方案和 PAV。
    • 如果所有单元格都有多个选项，则选择一个单元格和一个值，然后更新
      1. 并更新跟踪表、当前解决方案和 PAV

我们将使用表 6 来说明每个步骤，它是求解过程历史记录的一部分（称为 TRACKHIST）。

在第一次迭代 (CTR=1) 中，选择单元格 70（第 8 行、第 7 列、第 9 框）来为其分配值。只有候选值 (7)，并且该值被分配给单元格 70。此外，值 7 被添加到单元格 70 的先前分配值 (PAV) 向量中。

在第二次迭代中，单元格 30 被分配值 1。该单元格有两个候选值。最小的候选值被分配给单元格（只是一个任意规则，以使逻辑易于遵循）。

识别需要值的单元格并分配值的过程在迭代 (CTR) 20 之前工作正常。单元格 9 需要值，但候选数为零。有两种选择：

  • 这个难题没有答案。
  • 我们撤消（回溯）一些分配并采取另一条路径。

我们寻找与此最接近的单元格分配，其中有多个选项。在此示例中，这发生在迭代 18 处，其中单元格 5 被分配值 3，但单元格 5 有两个候选值 - 值 3 和 8。

在单元格 5 (CTR = 18) 和单元格 9 (CTR = 20) 之间，单元格 8 被分配值 4 (CTR=19)。我们将单元格 8 和 5 放回到“需要值”列表中。这是在第二个和第三个 CTR=20 条目中捕获的，其中值设置为 0。值 3 保留在单元格 5 的 PAV 向量中。也就是说，搜索引擎无法将值 3 分配给单元格 5。

搜索引擎再次启动以识别单元格 5 的值（3 不再是选项）并将值 8 分配给单元格 5 (CTR=21)。它一直持续到所有单元格都有值或者有一个单元格没有选项并且没有回溯路径。解决方案如表 7 所示。

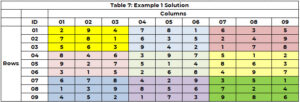
观察一下，当一个单元格有多个候选者时，这是并行处理的机会。

与 MILP 优化方案的比较

从表面上看，数独谜题的表现方式截然不同。人工智能方法使用整数，并且无论如何都是更严格、更直观的表示。此外，健全性检查器还提供有用的信息来制定更强大的配方。 MILP 表示是无穷无尽的 二进制 (0/1)。然而，鉴于现代 MILP 求解器的强大功能，二进制文件是强大的表示形式。

然而，在内部，MILP 求解器不保留二进制文件，而是使用稀疏数组方法来消除存储所有零。此外，解决二进制问题的算法直到 1980 世纪 1990 年代和 1983 年代才出现。 XNUMX 年的论文 克劳德、约翰逊和帕德伯格 关于二进制优化的第一个实用解决方案之一的报告。他们指出巧妙的预处理和分支定界方法对于成功解决方案至关重要。

最近约束规划和软件的使用呈爆炸式增长，例如 局部求解器 明确了将AI方法与线性规划、最小二乘等原始优化方法结合使用的重要性。

时间戳记：

更多来自 阿尔基耶娃