[آئینہ] چوکور ریاضی کے پروگرام: زیرو سے ہیرو تک

Vitalik Buterin کے ذریعے Vitalik Buterin بلاگ

یہ اس پوسٹ کا آئینہ ہے۔ https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

zk-SNARKs کے پیچھے ٹیکنالوجی میں حال ہی میں بہت دلچسپی ہوئی ہے، اور لوگ تیزی سے بے نقاب کرنے کی کوشش کر رہے ہیں۔ ایک ایسی چیز جسے بہت سے لوگ "چاند کی ریاضی" کہتے ہیں اس کی سمجھی جانے والی سراسر ناقابل فہم پیچیدگی کی وجہ سے۔ zk-SNARKs کو سمجھنا درحقیقت کافی مشکل ہے، خاص طور پر متحرک پرزوں کی بڑی تعداد کی وجہ سے جنہیں پوری چیز کے کام کرنے کے لیے ایک ساتھ آنے کی ضرورت ہے، لیکن اگر ہم ٹیکنالوجی کو ٹکڑے ٹکڑے کر دیں تو سمجھنا آسان ہو جاتا ہے۔

اس پوسٹ کا مقصد zk-SNARKs کا مکمل تعارف پیش کرنا نہیں ہے۔ یہ پس منظر کے علم کے طور پر فرض کرتا ہے کہ (i) آپ جانتے ہیں کہ zk-SNARKs کیا ہیں اور وہ کیا کرتے ہیں، اور (ii) کثیر الجہتی چیزوں کے بارے میں استدلال کرنے کے لیے کافی ریاضی جانتے ہیں (اگر بیان �(�)+�(�) =(�+�)(�)، جہاں � اور � polynomials ہیں، آپ کے لیے فطری اور واضح معلوم ہوتا ہے، پھر آپ صحیح سطح پر ہیں)۔ بلکہ، پوسٹ ٹیکنالوجی کے پیچھے مشینری کی گہرائی میں کھودتی ہے، اور پائپ لائن کے پہلے نصف حصے کی ممکنہ حد تک وضاحت کرنے کی کوشش کرتی ہے، جیسا کہ zk-SNARK کے محقق Eran Tromer نے یہاں کھینچا ہے:

یہاں کے مراحل کو دو حصوں میں تقسیم کیا جا سکتا ہے۔ سب سے پہلے، zk-SNARKs کا اطلاق کسی کمپیوٹیشنل مسئلہ پر براہ راست نہیں کیا جا سکتا۔ بلکہ، آپ کو مسئلہ کو کام کرنے کے لیے صحیح "فارم" میں تبدیل کرنا ہوگا۔ فارم کو "کواڈریٹک آرتھمیٹک پروگرام" (QAP) کہا جاتا ہے، اور کسی فنکشن کے کوڈ کو ان میں سے کسی ایک میں تبدیل کرنا بذات خود انتہائی غیر معمولی ہے۔ کسی فنکشن کے کوڈ کو QAP میں تبدیل کرنے کے عمل کے ساتھ ساتھ ایک اور عمل بھی ہے جو اس کے ساتھ چلایا جا سکتا ہے تاکہ اگر آپ کے پاس کوڈ میں کوئی ان پٹ ہو تو آپ ایک متعلقہ حل بنا سکتے ہیں (کبھی کبھی QAP کو "گواہ" کہا جاتا ہے)۔ اس کے بعد، اس گواہ کے لیے اصل "زیرو نالج پروف" بنانے کے لیے ایک اور کافی پیچیدہ عمل ہے، اور اس ثبوت کی تصدیق کے لیے ایک الگ عمل ہے کہ آپ کے ساتھ کوئی اور گزرتا ہے، لیکن یہ وہ تفصیلات ہیں جو اس پوسٹ کی گنجائش سے باہر ہیں۔ .

ہم جس مثال کا انتخاب کریں گے وہ ایک سادہ ہے: یہ ثابت کرنا کہ آپ مکعب مساوات کا حل جانتے ہیں: �3+�+5=35 (اشارہ: جواب 3 ہے)۔ یہ مسئلہ اتنا آسان ہے کہ نتیجے میں آنے والا QAP اتنا بڑا نہیں ہوگا جتنا خوفزدہ کرنے والا، لیکن اتنا غیر معمولی ہے کہ آپ دیکھ سکتے ہیں کہ تمام مشینری کام میں آتی ہے۔

آئیے اپنے فنکشن کو اس طرح لکھتے ہیں:

def qeval(x):
    y = x**3
    return x + y + 5

سادہ خصوصی مقصدی پروگرامنگ زبان جو ہم یہاں استعمال کر رہے ہیں بنیادی ریاضی (+, −, ⋅, /)، مستقل طاقت کی شرح (�7 لیکن �� نہیں) اور متغیر تفویض کو سپورٹ کرتی ہے، جو اتنی طاقتور ہے کہ آپ نظریاتی طور پر کر سکتے ہیں۔ اس کے اندر کوئی بھی کمپیوٹیشن (جب تک کمپیوٹیشنل مراحل کی تعداد پابند ہے؛ کسی لوپ کی اجازت نہیں ہے)۔ نوٹ کریں کہ modulo (%) اور موازنہ آپریٹرز (<, >, ≤, ≥) تعاون یافتہ نہیں ہیں، کیونکہ محدود چکری گروپ ریاضی میں ماڈیولو یا موازنہ کرنے کا کوئی موثر طریقہ نہیں ہے (اس کے لیے شکر گزار ہوں؛ اگر کوئی طریقہ تھا دونوں میں سے ایک کرنے کے لیے، پھر بیضوی وکر کی خفیہ نگاری اس سے زیادہ تیزی سے ٹوٹ جائے گی جتنا کہ آپ "بائنری سرچ" اور "چینی باقی تھیوریم" کہہ سکتے ہیں)۔

آپ زبان کو ماڈیولو اور موازنہ تک بڑھا سکتے ہیں بٹ سڑن (مثلاً 13=23+22+1) بطور معاون ان پٹ فراہم کر کے، ان سڑن کی درستی کو ثابت کر کے اور بائنری سرکٹس میں ریاضی کر سکتے ہیں۔ محدود فیلڈ ریاضی میں، مساوات (==) چیک کرنا بھی قابل عمل ہے اور حقیقت میں قدرے آسان، لیکن یہ دونوں تفصیلات ہیں جن میں ہم ابھی نہیں جائیں گے۔ ہم شرائط کی حمایت کرنے کے لیے زبان کو بڑھا سکتے ہیں (مثال کے طور پر اگر �<5:�=7؛ اور: �=9) کو ریاضی کی شکل میں تبدیل کر کے: �=7⋅(�<5)+9⋅(�≥5) ) اگرچہ نوٹ کریں کہ مشروط کے دونوں "راستوں" کو انجام دینے کی ضرورت ہوگی، اور اگر آپ کے پاس بہت سے نیسٹڈ کنڈیشنلز ہیں تو یہ بڑی مقدار میں اوور ہیڈ کا باعث بن سکتا ہے۔

آئیے اب مرحلہ وار اس عمل سے گزرتے ہیں۔ اگر آپ کوڈ کے کسی بھی ٹکڑے کے لیے یہ خود کرنا چاہتے ہیں، I یہاں ایک کمپائلر نافذ کیا۔ (صرف تعلیمی مقاصد کے لیے؛ ابھی تک حقیقی دنیا کے zk-SNARKs کے لیے QAPs بنانے کے لیے تیار نہیں!)

چپٹا کرنا

پہلا مرحلہ ایک "چپٹا" طریقہ کار ہے، جہاں ہم اصل کوڈ کو، جس میں من مانی پیچیدہ بیانات اور تاثرات شامل ہو سکتے ہیں، کو بیانات کی ایک ترتیب میں تبدیل کرتے ہیں جو دو شکلوں کے ہیں: �=� (جہاں � ایک متغیر یا عدد ہو سکتا ہے۔ ) اور �=� (��) � (جہاں �� +، −، ⋅، / اور � اور � متغیرات، اعداد یا خود ذیلی اظہار ہو سکتے ہیں)۔ آپ ان بیانات میں سے ہر ایک کو سرکٹ میں منطقی دروازے کی طرح سمجھ سکتے ہیں۔ مندرجہ بالا کوڈ کے لئے چپٹی عمل کا نتیجہ مندرجہ ذیل ہے:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

اگر آپ یہاں اصل کوڈ اور کوڈ پڑھتے ہیں، تو آپ کافی آسانی سے دیکھ سکتے ہیں کہ دونوں برابر ہیں۔

R1CS کے دروازے

اب، ہم اسے کسی چیز میں تبدیل کرتے ہیں جسے rank-1 constraint system (R1CS) کہتے ہیں۔ ایک R1CS تین ویکٹرز (�, �, �) کے گروپوں کی ایک ترتیب ہے، اور R1CS کا حل ایک ویکٹر ہے �، جہاں � کو مساوات �.�⋅�.�−�.�=0 کو پورا کرنا چاہیے، جہاں . ڈاٹ پروڈکٹ کی نمائندگی کرتا ہے - آسان الفاظ میں، اگر ہم "ایک ساتھ زپ کریں" � اور �، دونوں قدروں کو ایک ہی پوزیشن میں ضرب دیں، اور پھر ان مصنوعات کا مجموعہ لیں، پھر � اور � اور پھر � اور � ، پھر تیسرا نتیجہ پہلے دو نتائج کی پیداوار کے برابر ہے۔ مثال کے طور پر، یہ ایک مطمئن R1CS ہے:

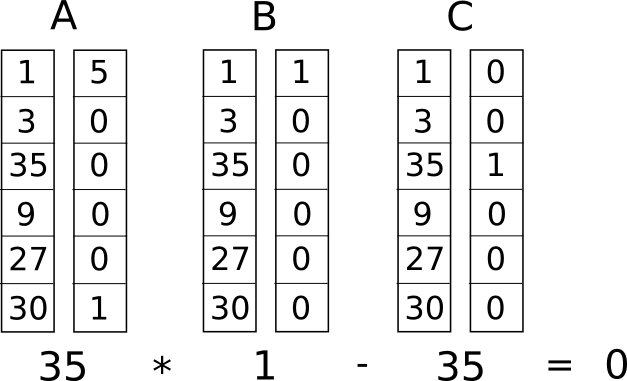
لیکن صرف ایک رکاوٹ رکھنے کے بجائے، ہمارے پاس بہت سی رکاوٹیں ہوں گی: ہر منطقی دروازے کے لیے ایک۔ منطقی دروازے کو (�,�,�) ٹرپل میں تبدیل کرنے کا ایک معیاری طریقہ ہے اس پر منحصر ہے کہ آپریشن کیا ہے (+, −, ⋅ یا /) اور آیا دلائل متغیر ہیں یا اعداد۔ ہر ویکٹر کی لمبائی سسٹم میں متغیرات کی کل تعداد کے برابر ہے، بشمول ایک ڈمی متغیر ~ ایک نمبر 1 کی نمائندگی کرنے والے پہلے انڈیکس میں، ان پٹ متغیرات، ایک ڈمی متغیر ~ آؤٹ آؤٹ پٹ کی نمائندگی کرتا ہے، اور پھر تمام انٹرمیڈیٹ متغیر (اوپر ���1 اور ���2)؛ ویکٹر عام طور پر بہت کم ہوتے ہیں، صرف ان سلاٹوں کو بھرتے ہیں جو متغیرات کے مطابق ہوتے ہیں جو کسی خاص لاجک گیٹ سے متاثر ہوتے ہیں۔

سب سے پہلے، ہم متغیر میپنگ فراہم کریں گے جسے ہم استعمال کریں گے:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

حل ویکٹر اس ترتیب میں ان تمام متغیرات کے لیے اسائنمنٹس پر مشتمل ہوگا۔

اب، ہم پہلے گیٹ کے لیے (�,�,�) ٹرپل دیں گے:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

آپ دیکھ سکتے ہیں کہ اگر سلوشن ویکٹر میں دوسری پوزیشن میں 3 اور چوتھی پوزیشن میں 9 ہے، تو حل ویکٹر کے باقی مواد سے قطع نظر، ڈاٹ پروڈکٹ چیک 3⋅3=9 پر ابل جائے گا، اور تو یہ گزر جائے گا. اگر حل ویکٹر کی دوسری پوزیشن میں −3 اور چوتھی پوزیشن میں 9 ہے، تو چیک بھی گزر جائے گا۔ درحقیقت، اگر سلوشن ویکٹر کی دوسری پوزیشن میں 7 اور چوتھی پوزیشن میں 49 ہے تو پھر بھی وہ چیک پاس ہو جائے گا — اس پہلے چیک کا مقصد صرف پہلے گیٹ کے ان پٹ اور آؤٹ پٹس کی مستقل مزاجی کی تصدیق کرنا ہے۔

اب، دوسرے دروازے پر چلتے ہیں:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

پہلے ڈاٹ پروڈکٹ چیک کی طرح ایک ہی انداز میں، یہاں ہم اس کی جانچ کر رہے ہیں ���1⋅�=�۔

اب، تیسرا دروازہ:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

یہاں، پیٹرن کچھ مختلف ہے: یہ حل ویکٹر میں پہلے عنصر کو دوسرے عنصر سے ضرب کر رہا ہے، پھر پانچویں عنصر سے، دو نتائج کو شامل کر رہا ہے، اور چیک کر رہا ہے کہ آیا رقم چھٹے عنصر کے برابر ہے۔ کیونکہ حل ویکٹر میں پہلا عنصر ہمیشہ ایک ہوتا ہے، یہ صرف ایک اضافی چیک ہے، یہ جانچنا کہ آؤٹ پٹ دو ان پٹ کے مجموعے کے برابر ہے۔

آخر میں، چوتھا دروازہ:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

یہاں، ہم آخری چیک کا جائزہ لے رہے ہیں، ~out =���2+5۔ ڈاٹ پروڈکٹ چیک حل ویکٹر میں چھٹے عنصر کو لے کر، پہلے عنصر سے پانچ گنا اضافہ کر کے کام کرتا ہے (یاد دہانی: پہلا عنصر 1 ہے، لہذا اس کا مؤثر طریقے سے مطلب ہے 5 شامل کرنا)، اور اسے تیسرے عنصر کے خلاف چیک کرنا، جہاں ہم آؤٹ پٹ متغیر کو ذخیرہ کریں۔

اور وہاں ہمارے پاس چار رکاوٹوں کے ساتھ R1CS ہے۔ گواہ صرف تمام متغیرات کی تفویض ہے، بشمول ان پٹ، آؤٹ پٹ اور اندرونی متغیرات:

[1, 3, 35, 9, 27, 30]

آپ اس کا حساب اوپر کے چپٹے کوڈ کو صرف "ایکسکیوٹ" کرکے، ان پٹ ویری ایبل اسائنمنٹ �=3 سے شروع کرکے، اور تمام انٹرمیڈیٹ ویری ایبلز اور آؤٹ پٹ کی قدریں ڈال کر ان کی گنتی کر سکتے ہیں۔

مکمل R1CS ایک ساتھ رکھا گیا ہے:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS سے QAP

اگلا مرحلہ اس R1CS کو لے کر اسے QAP فارم میں تبدیل کر رہا ہے، جو بالکل وہی منطق لاگو کرتا ہے سوائے ڈاٹ پروڈکٹس کے بجائے کثیر الثانیات کے استعمال کے۔ ہم یہ مندرجہ ذیل کرتے ہیں۔ ہم تین ڈگری-3 کثیر الاضلاع کے چھ سے چھ گروپوں کی لمبائی کے تین ویکٹروں کے چار گروپوں میں سے 3 جاتے ہیں، جہاں ہر ایک پر کثیر الاضلاع کا جائزہ لیتے ہیں۔ ایکس کوآرڈینیٹ رکاوٹوں میں سے ایک کی نمائندگی کرتا ہے۔ یعنی، اگر ہم کثیر ناموں کی تشخیص �=1 پر کرتے ہیں، تو ہمیں ویکٹرز کا پہلا سیٹ ملتا ہے، اگر ہم polynomials کا �=2 پر جائزہ لیتے ہیں، تو ہمیں ویکٹرز کا دوسرا سیٹ ملتا ہے، وغیرہ۔

ہم اس تبدیلی کو کسی ایسی چیز کا استعمال کر سکتے ہیں جسے a کہا جاتا ہے۔ لگرینج انٹرپولیشن. Lagrange انٹرپولیشن جو مسئلہ حل کرتا ہے وہ یہ ہے: اگر آپ کے پاس پوائنٹس کا ایک سیٹ ہے (یعنی (�,�) کوآرڈینیٹ جوڑوں، تو ان پوائنٹس پر Lagrange انٹرپولیشن کرنے سے آپ کو ایک کثیر الثانی ملتا ہے جو ان تمام پوائنٹس سے گزرتا ہے۔ ہم مسئلہ کو گل کر ایسا کرتے ہیں: ہر � کوآرڈینیٹ کے لیے، ہم ایک کثیر نام بناتے ہیں جس میں مطلوبہ � کوآرڈینیٹ ہوتا ہے � کوآرڈینیٹ پر اور � دیگر تمام � کوآرڈینیٹ پر 0 کا کوآرڈینیٹ ہوتا ہے جس میں ہماری دلچسپی ہے، اور پھر فائنل حاصل کرنے کے لیے نتیجہ ہم تمام کثیر الاضلاع کو ایک ساتھ شامل کرتے ہیں۔

آئیے ایک مثال کرتے ہیں۔ فرض کریں کہ ہم ایک کثیر الجہتی چاہتے ہیں جو (1,3), (2,2) اور (3,4) سے گزرے۔ ہم ایک کثیر نام بنا کر شروع کرتے ہیں جو (1,3), (2,0) اور (3,0) سے گزرتا ہے۔ جیسا کہ یہ پتہ چلتا ہے، ایک کثیر الجہتی بنانا جو �=1 پر "چپ جاتا ہے" اور دلچسپی کے دیگر مقامات پر صفر ہے؛ ہم صرف کرتے ہیں:

(x - 2) * (x - 3)

جو اس طرح لگتا ہے:

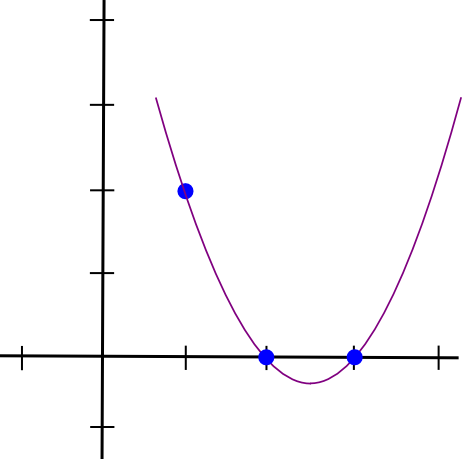
اب، ہمیں صرف اسے "ری سکیل" کرنے کی ضرورت ہے تاکہ x=1 کی اونچائی درست ہو:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

یہ ہمیں دیتا ہے:

1.5 * x**2 - 7.5 * x + 9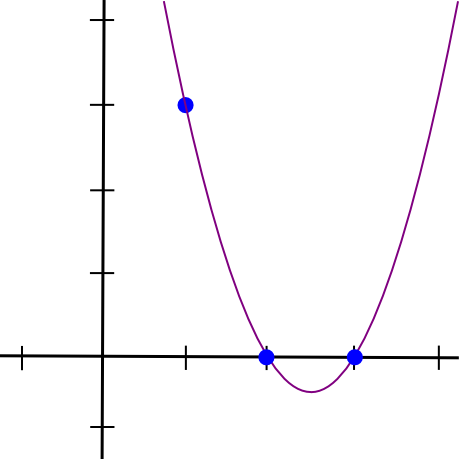

پھر ہم دوسرے دو پوائنٹس کے ساتھ بھی ایسا ہی کرتے ہیں، اور دو دیگر ملتے جلتے نظر آنے والے کثیر نام حاصل کرتے ہیں، سوائے اس کے کہ وہ �=2 کے بجائے �=3 اور �=1 پر "چپ جائیں"۔ ہم تینوں کو ایک ساتھ شامل کرتے ہیں اور حاصل کرتے ہیں:

1.5 * x**2 - 5.5 * x + 7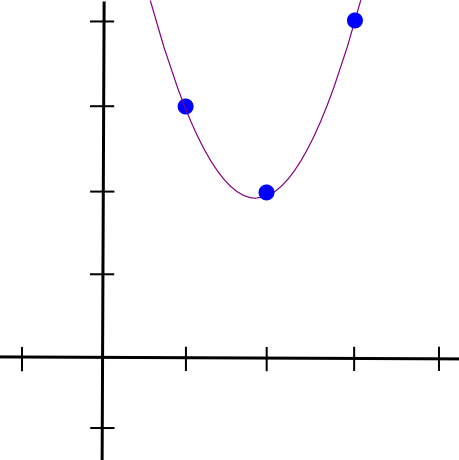

بالکل ان نقاط کے ساتھ جو ہم چاہتے ہیں۔ جیسا کہ اوپر بیان کیا گیا الگورتھم �(�3) وقت لیتا ہے، کیونکہ � پوائنٹس ہوتے ہیں اور ہر پوائنٹ کو �(�2) وقت کی ضرورت ہوتی ہے تاکہ کثیرالاضلاع کو ایک ساتھ ضرب کر سکے۔ تھوڑی سی سوچ کے ساتھ، اسے �(�2) وقت تک کم کیا جا سکتا ہے، اور بہت زیادہ سوچنے کے ساتھ، فاسٹ فوئیر ٹرانسفارم الگورتھم اور اس طرح کے استعمال سے، اسے اور بھی کم کیا جا سکتا ہے — ایک اہم اصلاح جب فنکشنز جو zk میں استعمال ہوتے ہیں۔ عملی طور پر SNARKs میں اکثر ہزاروں دروازے ہوتے ہیں۔

اب، آئیے اپنے R1CS کو تبدیل کرنے کے لیے Lagrange انٹرپولیشن کا استعمال کریں۔ ہم جو کرنے جا رہے ہیں وہ یہ ہے کہ ہر � ویکٹر سے پہلی قدر نکالیں، اس میں سے ایک کثیر الثانی بنانے کے لیے Lagrange انٹرپولیشن کا استعمال کریں (جہاں � پر کثیر نام کی جانچ کرنے سے آپ کو �th � ویکٹر کی پہلی قدر مل جاتی ہے)، اس عمل کو دہرائیں۔ ہر � اور � ویکٹر کی پہلی قدر کے لیے، اور پھر دوسری قدروں، تیسری، قدروں، وغیرہ کے لیے اس عمل کو دہرائیں۔ سہولت کے لیے میں ابھی جوابات فراہم کروں گا:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

گتانک صعودی ترتیب میں ہیں، اس لیے اوپر کا پہلا کثیر الجہتی اصل میں 0.833⋅�3—5⋅�2+9.166⋅�−5 ہے۔ کثیر ناموں کا یہ مجموعہ (علاوہ ایک Z کثیر نام جس کی میں بعد میں وضاحت کروں گا) اس مخصوص QAP مثال کے لیے پیرامیٹرز بناتا ہے۔ نوٹ کریں کہ اس وقت تک تمام کام ہر اس فنکشن کے لیے صرف ایک بار کرنے کی ضرورت ہے جس کی تصدیق کے لیے آپ zk-SNARKs استعمال کرنے کی کوشش کر رہے ہیں۔ QAP پیرامیٹرز تیار ہونے کے بعد، انہیں دوبارہ استعمال کیا جا سکتا ہے۔

آئیے ان تمام کثیر الاضلاع کو �=1 پر جانچنے کی کوشش کریں۔ �=1 پر کثیر الجہتی کا اندازہ کرنے کا سیدھا مطلب ہے تمام گتانکوں کو شامل کرنا (جیسا کہ 1�=1 سب کے لیے �)، لہذا یہ مشکل نہیں ہے۔ ہم حاصل:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

اور دیکھو، ہمارے پاس جو کچھ ہے وہ بالکل ویسا ہی ہے جیسا کہ پہلے لاجک گیٹ کے لیے تین ویکٹروں کا سیٹ جو ہم نے اوپر بنایا تھا۔

QAP کی جانچ کر رہا ہے۔

اب اس پاگل تبدیلی کا کیا فائدہ؟ جواب یہ ہے کہ R1CS میں رکاوٹوں کو انفرادی طور پر چیک کرنے کے بجائے، اب ہم چیک کر سکتے ہیں۔ ایک ہی وقت میں تمام پابندیاں ڈاٹ پروڈکٹ چیک کر کے کثیر الثانیات پر.

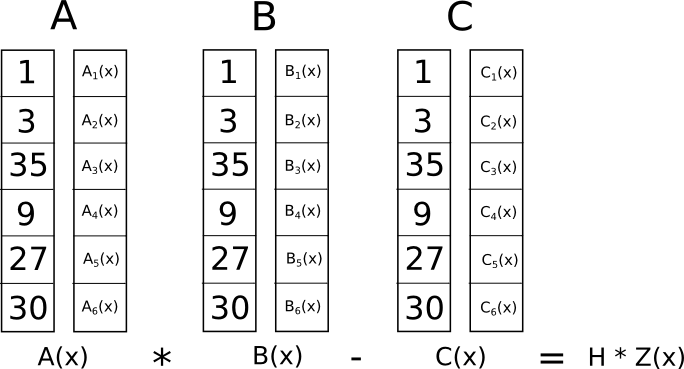
کیونکہ اس صورت میں ڈاٹ پروڈکٹ کی جانچ کثیر ناموں کے اضافے اور ضربوں کا ایک سلسلہ ہے، نتیجہ بذات خود ایک کثیر الثانی ہوگا۔ اگر نتیجہ خیز کثیر الثانی، ہر � کوآرڈینیٹ پر جانچا جاتا ہے جسے ہم نے اوپر لاجک گیٹ کی نمائندگی کرنے کے لیے استعمال کیا ہے، صفر کے برابر ہے، تو اس کا مطلب ہے کہ تمام چیک پاس ہو جاتے ہیں۔ اگر نتیجہ خیز کثیر الجہتی جائزہ لیا گیا کم از کم ایک کوآرڈینیٹ جو لاجک گیٹ کی نمائندگی کرتا ہے ایک غیر صفر قدر دیتا ہے، تو اس کا مطلب ہے کہ اس لاجک گیٹ کے اندر اور باہر جانے والی قدریں متضاد ہیں (یعنی گیٹ �=�⋅�� ہے �1 لیکن فراہم کردہ اقدار �=2، �1=2 اور �=5 ہو سکتی ہیں)۔

نوٹ کریں کہ نتیجہ خیز کثیر الثانی کا خود صفر ہونا ضروری نہیں ہے، اور حقیقت میں زیادہ تر صورتوں میں ایسا نہیں ہوگا؛ اس کا ان نکات پر کوئی بھی طرز عمل ہوسکتا ہے جو کسی منطقی دروازے سے مطابقت نہیں رکھتا ہے، جب تک کہ نتیجہ ان تمام نکات پر صفر ہو do کچھ گیٹ کے مطابق۔ درستگی کو جانچنے کے لیے، ہم درحقیقت ایک گیٹ سے متعلقہ ہر نقطہ پر کثیر الاضلاع �=�.�⋅�.�−�.� کا اندازہ نہیں لگاتے۔ اس کے بجائے، ہم � کو ایک اور کثیر الجہتی، � سے تقسیم کرتے ہیں، اور چیک کرتے ہیں کہ � یکساں طور پر تقسیم ہوتا ہے � – یعنی تقسیم �/� کوئی باقی نہیں چھوڑتا۔

� کی تعریف (�−1)⋅(�−2)⋅(�−3)… کے طور پر کی گئی ہے – سب سے آسان کثیر الجہتی جو منطقی دروازوں سے مطابقت رکھنے والے تمام پوائنٹس پر صفر کے برابر ہے۔ یہ الجبرا کی ایک ابتدائی حقیقت ہے۔ کوئی بھی کثیر الجہتی جو ان تمام نکات پر صفر کے برابر ہے اس کم سے کم کثیر کا ایک ضرب ہونا ضروری ہے، اور اگر کثیر نام � کا ضرب ہے تو ان پوائنٹس میں سے کسی پر بھی اس کی تشخیص صفر ہوگی۔ یہ مساوات ہمارے کام کو بہت آسان بنا دیتی ہے۔

اب، آئیے اصل میں ڈاٹ پروڈکٹ کو اوپر والے کثیر الثانیات کے ساتھ چیک کرتے ہیں۔ سب سے پہلے، درمیانی کثیر الثانیات:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

اب، �.�⋅�.�—�.�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

اب، کم سے کم کثیر الجہتی �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):

Z = [24, -50, 35, -10, 1]

اور اگر ہم اوپر کے نتیجہ کو � سے تقسیم کرتے ہیں تو ہمیں ملتا ہے:

h = t / Z = [-3.666, 17.055, -3.444]

بغیر کسی باقی کے۔

اور اس طرح ہمارے پاس QAP کا حل ہے۔ اگر ہم R1CS حل میں کسی بھی متغیر کو غلط ثابت کرنے کی کوشش کرتے ہیں جس سے ہم یہ QAP حل اخذ کر رہے ہیں - کہتے ہیں کہ، آخری کو 31 کے بجائے 30 پر سیٹ کریں، تو ہمیں ایک � پولنومیل ملتا ہے جو چیکوں میں سے ایک کو ناکام کرتا ہے (اس خاص میں صورت میں، �=3 پر نتیجہ 1 کے بجائے −0 کے برابر ہوگا) اور مزید یہ کہ � کا ضرب نہیں ہوگا۔ بلکہ، �/� کو تقسیم کرنے سے [−5.0,8.833,−4.5,0.666] کا بقیہ حصہ ملے گا۔

نوٹ کریں کہ مندرجہ بالا ایک آسان ہے؛ "حقیقی دنیا میں"، اضافہ، ضرب، گھٹاؤ اور تقسیم باقاعدہ اعداد کے ساتھ نہیں، بلکہ محدود فیلڈ عناصر کے ساتھ ہوگی - ایک ڈراونا قسم کی ریاضی جو خود سے مطابقت رکھتی ہے، لہذا تمام الجبری قوانین جنہیں ہم جانتے ہیں اور اب بھی پسند کرتے ہیں۔ درست رکھیں، لیکن جہاں تمام جوابات کچھ محدود سائز کے سیٹ کے عناصر ہیں، عام طور پر کچھ � کے لیے 0 سے �−1 کی حد کے اندر انٹیجرز ہوتے ہیں۔ مثال کے طور پر، اگر �=13، پھر 1/2=7 (اور 7⋅2=1)، 3⋅5=2، وغیرہ۔ محدود فیلڈ ریاضی کا استعمال گول کرنے کی غلطیوں کے بارے میں فکر کرنے کی ضرورت کو دور کرتا ہے اور نظام کو بیضوی منحنی خطوط کے ساتھ اچھی طرح سے کام کرنے کی اجازت دیتا ہے، جو کہ باقی zk-SNARK مشینری کے لیے ضروری ہے جو zk-SNARK پروٹوکول کو حقیقت میں محفوظ بناتی ہے۔

مجھے zk-SNARKs کے اندرونی کام کے بارے میں بہت سی تفصیلات بتانے میں مدد کرنے کے لیے Eran Tromer کا خصوصی شکریہ۔

• SEO سے چلنے والا مواد اور PR کی تقسیم۔ آج ہی بڑھا دیں۔
• پلیٹو ڈیٹا ڈاٹ نیٹ ورک ورٹیکل جنریٹو اے آئی۔ اپنے آپ کو بااختیار بنائیں۔ یہاں تک رسائی حاصل کریں۔
• پلیٹوآئ اسٹریم۔ ویب 3 انٹیلی جنس۔ علم میں اضافہ۔ یہاں تک رسائی حاصل کریں۔
• پلیٹو ای ایس جی۔ کاربن، کلین ٹیک، توانائی ، ماحولیات، شمسی، ویسٹ مینجمنٹ یہاں تک رسائی حاصل کریں۔
• پلیٹو ہیلتھ۔ بائیوٹیک اینڈ کلینیکل ٹرائلز انٹیلی جنس۔ یہاں تک رسائی حاصل کریں۔
• بلاک آفسیٹس۔ ماحولیاتی آفسیٹ ملکیت کو جدید بنانا۔ یہاں تک رسائی حاصل کریں۔
• ماخذ: افلاطون ڈیٹا انٹیلی جنس.