1Теоретична фізика, Університет Країни Басків UPV/EHU, ES-48080 Більбао, Іспанія
2Квантовий центр EHU, University of the Basque Country UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscay, Spain
3Міжнародний фізичний центр Доностії (DIPC), ES-20080 Сан-Себастьян, Іспанія
4IKERBASQUE, Баскський фонд науки, ES-48011 Більбао, Іспанія
5Інститут фізики та оптики твердого тіла, Науково-дослідний центр фізики Вігнера, HU-1525 Будапешт, Угорщина
6Інститут математики імені Альфреда Реньї, Reáltanoda u. 13-15., HU-1053 Будапешт, Угорщина
7Відділ аналізу та дослідження операцій, Інститут математики, Будапештський університет технології та економіки, Müegyetem rkp. 3., HU-1111 Будапешт, Угорщина
Вам цей документ цікавий чи ви хочете обговорити? Скайте або залиште коментар на SciRate.
абстрактний
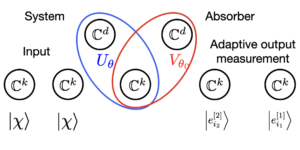
Ми визначаємо квантову відстань Вассерштейна таким чином, що оптимізація зв’язку виконується для дводольних розділених станів, а не для дводольних квантових станів загалом, і досліджуємо його властивості. Дивно, але ми виявили, що власна відстань пов’язана з квантовою інформацією Фішера. Ми представляємо транспортну карту, що відповідає оптимальному двосторонньому роздільному стану. Ми обговорюємо, як введена квантова відстань Вассерштейна пов’язана з критеріями виявлення квантової заплутаності. Ми визначаємо дисперсійні величини, які можна отримати з квантової відстані Вассерштейна шляхом заміни мінімізації квантових станів на максимізацію. Ми поширюємо наші результати на сімейство узагальнених квантових інформаційних величин Фішера.
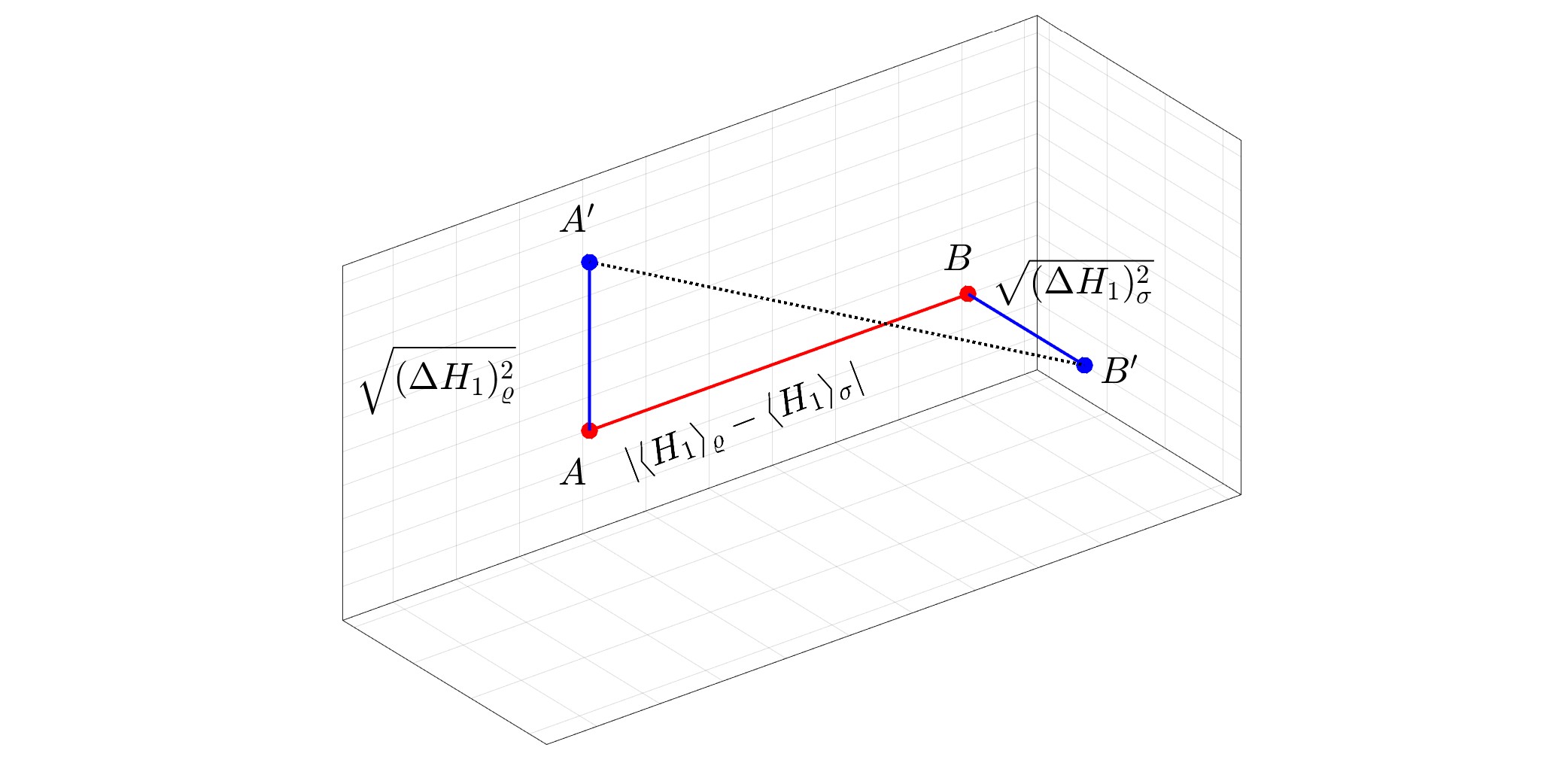
Рекомендоване зображення: Геометричне представлення квантової відстані Вассерштейна між чистим станом $varrho$ і змішаним станом $sigma$ для $N=1.$ Квантова відстань Вассерштейна дорівнює $1/sqrt2$, помноженій на звичайну евклідову відстань між $A'$ і $B'.$
Популярне резюме
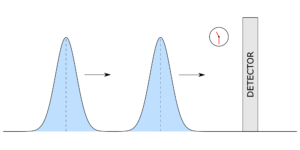
Відстані відіграють центральну роль у математиці, фізиці та інженерії. Фундаментальна проблема ймовірності та статистики полягає в тому, щоб знайти корисні міри відстані між двома розподілами ймовірностей. На жаль, багато понять відстані між розподілами ймовірностей, скажімо p(x) і q(x), є максимальними, якщо вони не перекриваються одне з одним, тобто одне завжди дорівнює нулю, коли інше відмінне від нуля. Це непрактично для багатьох програм. Наприклад, повертаючись до аналогії з піском, дві купи піску, які не перекриваються, здаються однаково віддаленими одна від одної, незалежно від того, чи становить їх відстань 10 км чи 100 км. Теорія оптимального транспорту є способом побудови альтернативного поняття відстані між розподілами ймовірностей, так званої відстані Вассерштейна. Він може бути немаксимальним, навіть якщо розподіли не накладаються один на одного, він чутливий до базової метрики (тобто, вартості транспортування), і, по суті, він виражає зусилля, які нам потрібні, щоб рухатися одне до іншого, ніби це були піщані пагорби.
Нещодавно було визначено квантову відстань Вассерштейна, узагальнюючи класичну відстань Вассерштейна. Він заснований на мінімізації функції вартості над квантовими станами дводольної квантової системи. Він має властивість, аналогічну згаданій вище в квантовому світі. Він може бути немаксимальним для ортогональних станів, що корисно, наприклад, коли нам потрібно навчити квантовим даним алгоритм.
Як ми можемо очікувати, квантова відстань Вассерштейна також має властивості, які дуже відрізняються від властивостей її класичного аналога. Наприклад, коли ми вимірюємо відстань квантового стану до самого себе, вона може бути відмінною від нуля. Хоча це вже викликає здивування, було також виявлено, що власна відстань пов’язана з викривленою інформацією Вігнера-Янасе, представленою в 1963 році лауреатом Нобелівської премії Е. П. Вігнером, який має важливий внесок в основи квантової фізики, і М. М. Янасе.
У нашій статті ми дивимося на цю таємничу знахідку з іншого боку. Ми обмежуємо згадану вище мінімізацію до так званих сепарабельних станів. Це квантові стани, які не містять заплутаності. Ми виявили, що власна відстань стає квантовою інформацією Фішера, величиною, центральною в квантовій метрології та теорії квантової оцінки, яка з’являється, наприклад, у знаменитій межі Крамера-Рао. Досліджуючи властивості такої відстані Вассерштейна, наша робота відкриває шлях до зв’язку теорії квантової відстані Вассерштейна з теорією квантової заплутаності.
► Дані BibTeX
► Список літератури
[1] Г. Монж. «Mémoire sur la héory des déblais et des remblais». Mémoires de l'Académie Royale de Sciences de Paris (1781).
[2] Л. Канторович. «Про переміщення мас». Наука управління 5, 1–4 (1958). url: http:///www.jstor.org/stable/2626967.
http:///www.jstor.org/stable/2626967
[3] Еммануель Буассар, Тібо Ле Гуїк і Жан-Мішель Лубес. “Оцінка шаблону розподілу з метрикою Вассерштейна”. Бернуллі 21, 740–759 (2015).
https:///doi.org/10.3150/13-bej585
[4] Олег Бутковський. “Субгеометричні швидкості збіжності марковських процесів у метриці Вассерштейна”. Енн апл. ймовірно 24, 526–552 (2014).
https:///doi.org/10.1214/13-AAP922
[5] М. Хайрер, Ж.-К. Маттінглі та М. Шойцова. “Асимптотичний зв’язок і загальна форма теореми Гарріса із застосуваннями до стохастичних рівнянь із запізненням”. ймовірно Теорія відн. Поля 149, 223–259 (2011).
https://doi.org/10.1007/s00440-009-0250-6
[6] М. Хайрер і Дж. К. Матінглі. “Спектральні розриви у відстанях Вассерштейна та двовимірні стохастичні рівняння Нав’є-Стокса”. Енн ймовірно 2, 36–2050 (2091).
https:///doi.org/10.1214/08-AOP392
[7] А. Фігаллі, Ф. Маджі та А. Прателлі. «Підхід масового транспорту до кількісних ізопериметричних нерівностей». Винаходити. математика 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z
[8] А. Фігаллі та Ф. Маджі. “Про форму рідких крапель і кристалів у режимі малих мас”. Арк. Раціон. мех. анальний 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x
[9] Дж. Лотт і Ч. Віллані. «Кривина Річчі для просторів метричної міри через оптимальний транспорт». Енн математики. 169 (3), 903–991 (2009).
https:///doi.org/10.48550/arXiv.math/0412127
[10] Макс-К. фон Ренесс і Карл-Теодор Штурм. «Транспортні нерівності, градієнтні оцінки, ентропія та кривизна Річчі». зв'язок Чисте застосування математика 58, 923–940 (2005).
https:///doi.org/10.1002/cpa.20060
[11] Карл-Теодор Штурм. “Про геометрію просторів метричних мір I”. Acta Math. 196, 65–131 (2006).
https://doi.org/10.1007/s11511-006-0002-8
[12] Карл-Теодор Штурм. “Про геометрію просторів метричних мір II”. Acta Math. 196, 133–177 (2006).
https://doi.org/10.1007/s11511-006-0003-7
[13] Бенуа Клокнер. “Геометричне дослідження просторів Вассерштейна: евклідові простори”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https:///doi.org/10.2422/2036-2145.2010.2.03
[14] György Pál Gehér, Tamás Titkos і Dániel Virosztek. “Про ізометричні вкладення просторів Вассерштейна – дискретний випадок”. J. Math. анальний апл. 480, 123435 (2019).
https:///doi.org/10.1016/j.jmaa.2019.123435
[15] György Pál Gehér, T. Titkos, Dániel Virosztek. “Ізометричне дослідження просторів Вассерштейна – дійсна лінія”. пер. амер. математика Соц. 373, 5855–5883 (2020).
https:///doi.org/10.1090/tran/8113
[16] György Pál Gehér, Tamás Titkos і Dániel Virosztek. “Група ізометрії просторів Вассерштейна: гільбертівський випадок”. Дж. Лонд. математика Соц. 106, 3865–3894 (2022).
https:///doi.org/10.1112/jlms.12676
[17] György Pál Gehér, Tamás Titkos і Dániel Virosztek. “Ізометрична жорсткість торів і сфер Вассерштейна”. Математика 69, 20–32 (2023).
https:///doi.org/10.1112/mtk.12174
[18] Ґергей Кісс і Тамаш Тіткос. “Ізометрична жорсткість просторів Вассерштейна: метричний випадок графа”. Proc. Am. математика Соц. 150, 4083–4097 (2022).
https:///doi.org/10.1090/proc/15977
[19] György Pál Gehér, Tamás Titkos і Dániel Virosztek. “Про екзотичний ізометричний потік квадратичного простору Вассерштейна над реальною прямою”. Лінійна алгебра Appl. (2023).
https:///doi.org/10.1016/j.laa.2023.02.016
[20] С. Колоурі, С. Р. Парк і Г. К. Роде. «Інтегральне перетворення розподілу Радона та його застосування до класифікації зображень». IEEE Trans. Обробка зображення. 25, 920–934 (2016).
https:///doi.org/10.1109/TIP.2015.2509419
[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek і GK Rohde. «Лінійна оптимальна транспортна структура для кількісної оцінки та візуалізації варіацій у наборах зображень». Міжн. Ж. Обчисл. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z
[22] С. Колоурі, С. Парк, М. Торп, Д. Слєпцев, Г. К. Роде. «Оптимальний масовий транспорт: обробка сигналів і програми машинного навчання». Журнал IEEE Signal Processing Magazine 34, 43–59 (2017).
https:///doi.org/10.1109/MSP.2017.2695801
[23] А. Грамфорт, Г. Пейре та М. Кутурі. «Швидке оптимальне транспортне усереднення даних нейровізуалізації». Обробка інформації в медичній візуалізації. IPMI 2015. Конспект лекцій з інформатики 9123, 261–272 (2015).
https://doi.org/10.1007/978-3-319-19992-4_20
[24] Z. Su, W. Zeng, Y. Wang, ZL Lu та X. Gu. «Класифікація форм за допомогою відстані Вассерштейна для аналізу морфометрії мозку». Обробка інформації в медичній візуалізації. IPMI 2015. Конспект лекцій з інформатики 24, 411–423 (2015).
https://doi.org/10.1007/978-3-319-19992-4_32
[25] Мартін Арджовскі, Суміт Чінтала та Леон Боту. «Генеративні змагальні мережі Вассерштайна». У Doina Precup і Yee Whye Teh, редактори, Proceedings of the 34th International Conference on Machine Learning. Том 70 Proceedings of Machine Learning Research, сторінки 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875
[26] Т. А. Ель Моселхі та Ю. М. Марзук. “Байєсівський висновок з оптимальними картами”. Ж. Обчисл. фіз. 231, 7815–7850 (2012).
https:///doi.org/10.1016/j.jcp.2012.07.022
[27] Габріель Пейре та Марко Кутурі. «Оптимальний обчислювальний транспорт: із застосуванням до науки про дані». знайдено. Тенденції машинного навчання. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073
[28] Чарлі Фрогнер, Чіюан Чжан, Хоссейн Мобахі, Маурісіо Арайя та Томазо А Поджіо. «Навчання з втратою Вассерштайна». У C. Cortes, N. Lawrence, D. Lee, M. Sugiyama та R. Garnett, редактори, Досягнення в нейронних системах обробки інформації. Том 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439
[29] А. Рамдас, Н. Г. Тріллос і М. Кутурі. «Про двовибіркове тестування Вассерштейна та пов’язані сімейства непараметричних тестів». Ентропія 19, 47. (2017).
https:///doi.org/10.3390/e19020047
[30] С. Срівастава, К. Лі та Д. Б. Дансон. «Масштабований Байєс через Барицентр у просторі Вассерштайн». Й. Мах. вчитися. рез. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880
[31] Кароль Жичковський і Войцех Сломчинський. «Відстань Монжа між квантовими станами». J. Phys. В: Математика. Gen. 31, 9095–9104 (1998).
https://doi.org/10.1088/0305-4470/31/45/009
[32] Кароль Жичковський і Войцех Сломчинський. “Метрика Монжа на сфері та геометрії квантових станів”. J. Phys. В: Математика. Gen. 34, 6689–6722 (2001).
https://doi.org/10.1088/0305-4470/34/34/311
[33] Інгемар Бенгтссон і Кароль Жичковскі. “Геометрія квантових станів: вступ до квантової заплутаності”. Cambridge University Press. (2006).
https:///doi.org/10.1017/CBO9780511535048
[34] П. Біане та Д. Войкулеску. «Вільний ймовірнісний аналог метрики Вассерштейна на просторі слідів-станів». ГАФА, Геом. Функція. анальний 11, 1125–1138 (2001).
https://doi.org/10.1007/s00039-001-8226-4
[35] Ерік А. Карлен і Ян Маас. «Аналог 2-метрики Вассерштейна в некомутативній ймовірності, за якої ферміонне рівняння Фоккера-Планка є градієнтним потоком для ентропії». Комун. математика фіз. 331, 887–926 (2014).
https://doi.org/10.1007/s00220-014-2124-8
[36] Ерік А. Карлен і Ян Маас. “Градієнтний потік та ентропійні нерівності для квантових марковських напівгруп з детальним балансом”. J. Функц. анальний 273, 1810–1869 (2017).
https:///doi.org/10.1016/j.jfa.2017.05.003
[37] Ерік А. Карлен і Ян Маас. “Некомутативне числення, оптимальні транспортні та функціональні нерівності в дисипативних квантових системах”. J. Stat. фіз. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w
[38] Ніланджана Датта та Камбіз Рузе. «Концентрація квантових станів із квантових функціональних нерівностей і нерівностей транспортних витрат». J. Math. фіз. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210
[39] Ніланджана Датта та Камбіз Рузе. «Зв’язок відносної ентропії, оптимального транспорту та інформації Фішера: квантова нерівність HWI». Енн Анрі Пуанкаре 21, 2115–2150 (2020).
https://doi.org/10.1007/s00023-020-00891-8
[40] Франсуа Голс, Клеман Муо та Тьєррі Поль. “Про середнє поле та класичні межі квантової механіки”. Комун. математика фіз. 343, 165–205 (2016).
https://doi.org/10.1007/s00220-015-2485-7
[41] Франсуа Голс і Тьєррі Поль. “Рівняння Шредінгера в середньому полі та напівкласичному режимі”. Арк. Раціон. мех. анальний 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x
[42] Франсуа Голс і Тьєррі Поль. “Хвильові пакети та квадратична відстань Монжа-Канторовича в квантовій механіці”. Comptes Rendus Math. 356, 177–197 (2018).
https:///doi.org/10.1016/j.crma.2017.12.007
[43] Франсуа Голс. “Квантова проблема $N$-тіла в середньому полі та напівкласичному режимі”. Філ. пер. R. Soc. A 376, 20170229 (2018).
https:///doi.org/10.1098/rsta.2017.0229
[44] Е. Каліоті, Ф. Голзе, Т. Поль. «Квантовий оптимальний транспорт дешевший». J. Stat. фіз. 181, 149–162 (2020).
https://doi.org/10.1007/s10955-020-02571-7
[45] Емануеле Каліоті, Франсуа Голс і Тьєррі Поль. «До оптимального транспорту для квантових густин». arXiv:2101.03256 (2021).
https:///doi.org/10.48550/arXiv.2101.03256
arXiv: 2101.03256
[46] Джакомо Де Пальма і Даріо Тревісан. «Квантовий оптимальний транспорт з квантовими каналами». Енн Анрі Пуанкаре 22, 3199–3234 (2021).
https://doi.org/10.1007/s00023-021-01042-3
[47] Джакомо Де Пальма, Мілад Марвіан, Даріо Тревізан і Сет Ллойд. «Квантова відстань Вассерштейна порядку 1». IEEE Trans. Інф. Теорія 67, 6627–6643 (2021).
https:///doi.org/10.1109/TIT.2021.3076442
[48] Шмуель Фрідланд, Міхал Екштайн, Сем Коул і Кароль Жичковський. “Квантова проблема Монжа–Канторовича та транспортна відстань між матрицями густини”. фіз. Преподобний Летт. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402
[49] Сем Коул, Міхал Екштайн, Шмуель Фрідланд і Кароль Жичковський. «Квантовий оптимальний транспорт». arXiv:2105.06922 (2021).
https:///doi.org/10.48550/arXiv.2105.06922
arXiv: 2105.06922
[50] Р. Бістронь, М. Екштайн і К. Жичковський. “Монотонність квантової відстані 2-Вассерштейна”. J. Phys. В: Математика. Теор. 56, 095301 (2023).
https://doi.org/10.1088/1751-8121/acb9c8
[51] Дьєрдь Пал Гехер, Йожеф Пітрік, Тамаш Тіткос і Даніель Віроштек. «Квантові ізометрії Вассерштейна в просторі станів кубіта». J. Math. анальний апл. 522, 126955 (2023).
https:///doi.org/10.1016/j.jmaa.2022.126955
[52] Лу Лі, Кайфен Бу, Дакс Еншань Ко, Артур Джаффе та Сет Ллойд. “Складність квантових схем Вассерштейна”. arXiv: 2208.06306 (2022).
https:///doi.org/10.48550/arXiv.2208.06306
[53] Бобак Туссі Кіані, Джакомо Де Пальма, Мілад Марвіан, Цзи-Вен Лю та Сет Ллойд. «Вивчення квантових даних за допомогою відстаней квантового землероба». Квантова наука. технол. 7, 045002 (2022).
https://doi.org/10.1088/2058-9565/ac79c9
[54] EP Wigner і Mutsuo M. Yanase. “Інформативність розсилок”. Proc. Natl. акад. Sci. США 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910
[55] Ришард Городецький, Павло Городецький, Міхал Городецький та Кароль Городецький. «Квантова заплутаність». Rev. Mod. фіз. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865
[56] Отфрід Гюне та Геза Тот. «Виявлення заплутаності». фіз. 474, 1–75 (2009).
https:///doi.org/10.1016/j.physrep.2009.02.004
[57] Ніколай Фрііс, Джузеппе Вітальяно, Мехул Малік і Маркус Хубер. «Сертифікація заплутаності від теорії до експерименту». Нац. Rev. Phys. 1, 72–87 (2019).
https://doi.org/10.1038/s42254-018-0003-5
[58] Вітторіо Джованетті, Сет Ллойд і Лоренцо Макконе. «Квантово-розширені вимірювання: перевищення стандартної квантової межі». Наука 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149
[59] Маттео Г. А. Паріс. «Квантова оцінка для квантової технології». Міжн. J. Quant. Інф. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839
[60] Рафал Демкович-Добжанський, Марцін Яжина та Ян Колодинський. «Розділ четвертий – Квантові межі в оптичній інтерферометрії». Прог. Оптика 60, 345 – 435 (2015). arXiv:1405.7703.
https:///doi.org/10.1016/bs.po.2015.02.003
arXiv: 1405.7703
[61] Лука Пецце і Аугусто Смерці. “Квантова теорія оцінки фази”. У GM Tino та MA Kasevich, редактори, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Course 188, Varenna). Сторінки 691–741. IOS Press, Амстердам (2014). arXiv:1411.5164.
arXiv: 1411.5164
[62] Геза Тот і Денес Петц. “Екстремальні властивості дисперсії та квантова інформація Фішера”. фіз. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324
[63] Сіксія Ю. «Квантова інформація Фішера як опуклий дах дисперсії». arXiv:1302.5311 (2013).
https:///doi.org/10.48550/arXiv.1302.5311
arXiv: 1302.5311
[64] Геза Тот і Флоріан Фровіс. “Співвідношення невизначеності з дисперсією та квантовою інформацією Фішера на основі опуклих розкладів матриць густини”. фіз. Дослідження 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075
[65] Шао-Хен Чіу та Мануель Гесснер. “Покращення співвідношень сумарної невизначеності з квантовою інформацією Фішера”. фіз. Дослідження 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076
[66] Хельстром. “Теорія квантового виявлення та оцінювання”. Academic Press, Нью-Йорк. (1976). url: www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5.
https://www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5
[67] А. С. Холево. “Імовірнісні та статистичні аспекти квантової теорії”. Північна Голландія, Амстердам. (1982).
[68] Семюел Л. Браунштейн і Карлтон М. Кейвс. «Статистична відстань і геометрія квантових станів». фіз. Преподобний Летт. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439
[69] Семюел Л. Браунштейн, Карлтон М. Кейвс і Джерард Дж. Мілберн. “Узагальнені співвідношення невизначеності: теорія, приклади та лоренц-інваріантність”. Енн фіз. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040
[70] Денес Петц. “Квантова теорія інформації та квантова статистика”. Шпрінгер, Берлін, Гейлдерберг. (2008).
https://doi.org/10.1007/978-3-540-74636-2
[71] Геза Тот і Ягоба Апелланіз. «Квантова метрологія з точки зору квантової інформаційної науки». J. Phys. В: Математика. Теор. 47, 424006 (2014).
https://doi.org/10.1088/1751-8113/47/42/424006
[72] Лука Пецце, Аугусто Смерзі, Маркус К. Оберталер, Роман Шмід і Філіп Тройтлайн. “Квантова метрологія з некласичними станами атомних ансамблів”. Rev. Mod. фіз. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005
[73] Марко Барб'єрі. “Оптична квантова метрологія”. PRX Quantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202
[74] Золтан Лека та Денес Петц. “Деякі розкладання дисперсій матриці”. ймовірно математика статист. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707
[75] Денес Петц і Даніель Віроштек. “Характеристична теорема для дисперсій матриці”. Acta Sci. математика (Сегед) 80, 681–687 (2014).
https:///doi.org/10.14232/actasm-013-789-z
[76] Акіо Фудзівара та Хіроші Імаї. «Пучок волокон над різновидами квантових каналів і його застосування до квантової статистики». J. Phys. В: Математика. Теор. 41, 255304 (2008).
https://doi.org/10.1088/1751-8113/41/25/255304
[77] Б. М. Ешер, Р. Л. де Матос Фільо, Л. Давидович. «Загальна основа для оцінки межі кінцевої точності в шумовій квантово-посиленій метрології». Нац. фіз. 7, 406–411 (2011).
https:///doi.org/10.1038/nphys1958
[78] Рафал Демкович-Добжанський, Ян Колодинський і Мадалін Гуце. «Невловима межа Гейзенберга в квантово-розширеній метрології». Нац. Комун. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067
[79] Іман Марвіан. «Операційна інтерпретація квантової інформації Фішера в квантовій термодинаміці». фіз. Преподобний Летт. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502
[80] Рейнхард Ф. Вернер. “Квантові стани з кореляціями Ейнштейна-Подольського-Розена, які допускають модель прихованої змінної”. фіз. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277
[81] К. Екерт, Й. Шліман, Д. Брюсс, М. Левенштейн. “Квантові кореляції в системах нерозрізнених частинок”. Енн фіз. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268
[82] Цубаса Ічікава, Тосіхіко Сасакі, Ізумі Цуцуі та Нобухіро Йонедзава. “Обмінна симетрія та багатостороння заплутаність”. фіз. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105
[83] Павло Городецький. “Критерій роздільності та нероздільні змішані стани з позитивною частковою транспозицією”. фіз. Lett. A 232, 333–339 (1997).
https://doi.org/10.1016/S0375-9601(97)00416-7
[84] Ашер Перес. “Критерій роздільності для матриць щільності”. фіз. Преподобний Летт. 77, 1413–1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413
[85] Павло Городецький, Міхал Городецький та Ришард Городецький. «Можна активувати пов’язане заплутування». фіз. Преподобний Летт. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056
[86] Геза Тот і Тамаш Вертеші. «Квантові стани з позитивним частковим транспонуванням корисні для метрології». фіз. Преподобний Летт. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506
[87] Скотт Хілл і Вільям К. Вуттерс. «Заплутаність пари квантових бітів». фіз. Преподобний Летт. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022
[88] Вільям К. Вуттерс. “Заплутаність формування довільного стану двох кубітів”. фіз. Преподобний Летт. 80, 2245–2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245
[89] Девід П. ДіВінченцо, Крістофер А. Фукс, Хідео Мабучі, Джон А. Смолін, Ашіш Тапліял та Армін Ульманн. «Заплутування допомоги». quant-ph/9803033 (1998).
https:///doi.org/10.48550/arXiv.quant-ph/9803033
arXiv: quant-ph / 9803033
[90] Джон А. Смолін, Френк Верстрете та Андреас Вінтер. «Плетіння допомоги та багатостороння державна перегонка». фіз. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317
[91] Хольгер Ф. Гофман і Шигекі Такеучі. “Порушення локальних співвідношень невизначеності як ознака заплутаності”. фіз. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103
[92] Отфрід Гюне. «Характеристика заплутаності через співвідношення невизначеності». фіз. Преподобний Летт. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903
[93] Отфрід Гюне, Матьяш Мехлер, Геза Тот і Петер Адам. «Критерії заплутаності, засновані на співвідношеннях локальної невизначеності, суворо сильніші, ніж критерій обчислюваної перехресної норми». фіз. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301
[94] Джузеппе Вітальяно, Філіп Гіллус, Іньїго Л. Егускіза та Геза Тот. “Нерівності стискання обертів для довільного обертання”. фіз. Преподобний Летт. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502
[95] А. Р. Едмондс. “Кутовий момент у квантовій механіці”. Princeton University Press. (1957).
https: / / doi.org/ 10.1515 / 9781400884186
[96] Геза Тот. «Виявлення заплутаності в оптичних решітках бозонних атомів за допомогою колективних вимірювань». фіз. Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327
[97] Геза Тот, Крістіан Кнапп, Отфрід Гюне та Ганс Дж. Брігель. «Оптимальні нерівності обертового стискання виявляють зв’язане заплутування в спінових моделях». фіз. Преподобний Летт. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405
[98] Геза Тот і Морган В. Мітчелл. “Генерація макроскопічних синглетних станів в атомних ансамблях”. New J. Phys. 12, 053007 (2010).
https://doi.org/10.1088/1367-2630/12/5/053007
[99] Геза Тот. “Виявлення багаточастинної заплутаності в околицях симетричних станів Дікке”. J. Opt. Соц. Am. B 24, 275–282 (2007).
https:///doi.org/10.1364/JOSAB.24.000275
[100] Геза Тот, Тобіас Мородер і Отфрід Гюне. «Оцінка показників заплутаності опуклого даху». фіз. Преподобний Летт. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501
[101] Лівен Ванденберге та Стівен Бойд. “Напіввизначене програмування”. SIAM Review 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003
[102] Геза Тот. «Багатостороннє заплутування та високоточна метрологія». фіз. Rev. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322
[103] Філіп Гіллус, Вєслав Ласковскі, Роланд Крішек, Крістіан Швеммер, Вітлеф Вєчорек, Гаральд Вайнфуртер, Лука Пецце та Аугусто Смерзі. «Інформація Фішера та багаточастинкова заплутаність». фіз. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321
[104] Геза Тот, Тамаш Вертеші, Павло Городецький та Ришард Городецький. «Активація прихованої метрологічної корисності». фіз. Преподобний Летт. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402
[105] AC Doherty, Pablo A. Parrilo та Federico M. Spedalieri. «Розрізнення роздільних і заплутаних станів». фіз. Преподобний Летт. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904
[106] Ендрю С. Доерті, Пабло А. Парріло та Федеріко М. Спедальєрі. «Повне сімейство критеріїв роздільності». фіз. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308
[107] Ендрю С. Доерті, Пабло А. Парріло та Федеріко М. Спедальєрі. «Виявлення багатостороннього заплутування». фіз. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333
[108] Гарольд Олів'є та Войцех Х. Зурек. «Квантовий розлад: міра квантовості кореляцій». фіз. Преподобний Летт. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901
[109] Л. Хендерсон і В. Ведрал. “Класичні, квантові та повні кореляції”. J. Phys. В: Математика. Gen. 34, 6899 (2001).
https://doi.org/10.1088/0305-4470/34/35/315
[110] Аніндіта Бера, Тамогна Дас, Дебасіс Садхухан, Судіпто Сінгха Рой, Адіті Сен(Де) та Уджвал Сен. «Квантовий розбрат та його союзники: огляд нещодавнього прогресу». Rep. Prog. фіз. 81, 024001 (2017).
https:///doi.org/10.1088/1361-6633/aa872f
[111] Денес Петц. “Коваріація та інформація Фішера в квантовій механіці”. J. Phys. В: Математика. Gen. 35, 929 (2002).
https://doi.org/10.1088/0305-4470/35/4/305
[112] Паоло Гібіліско, Фуміо Хіай та Денес Петц. “Квантова коваріація, квантова інформація Фішера та співвідношення невизначеностей”. IEEE Trans. Інф. Теорія 55, 439–443 (2009).
https:///doi.org/10.1109/TIT.2008.2008142
[113] Д. Петц і Ч. Гінеа. «Введення в квантову інформацію Фішера». Том 27, сторінки 261–281. Всесвітній науковий. (2011).
https:///doi.org/10.1142/9789814338745_0015
[114] Френк Хансен. «Метрична скоригована інформація про перекіс». Proc. Natl. акад. Sci. США 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105
[115] Паоло Гібіліско, Давіде Гіроламі та Френк Гансен. «Уніфікований підхід до локальної квантової невизначеності та інтерферометричної потужності за допомогою метрично скоригованої інформації про викривлення». Ентропія 23, 263 (2021).
https:///doi.org/10.3390/e23030263
[116] MATLAB. «9.9.0.1524771(r2020b)». The MathWorks Inc. Natick, Массачусетс (2020).
[117] MOSEK ApS. «Набір інструментів оптимізації MOSEK для посібника MATLAB. Версія 9.0”. (2019). url: docs.mosek.com/9.0/toolbox/index.html.
https:///docs.mosek.com/9.0/toolbox/index.html
[118] Й. Лефберг. “YALMIP: інструментарій для моделювання та оптимізації в MATLAB”. У матеріалах конференції CACSD. Тайбей, Тайвань (2004).
[119] Геза Тот. “QUBIT4MATLAB V3.0: програмний пакет для квантової інформатики та квантової оптики для MATLAB”. обчис. фіз. Комун. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007
[120] Пакет QUBIT4MATLAB доступний за адресою https:///www.mathworks.com/matlabcentral/ fileexchange/8433 та на особистій домашній сторінці https://gtoth.eu/qubit4matlab.html.
https:///www.mathworks.com/matlabcentral/fileexchange/8433
Цитується
[1] Лоран Лафлеш, «Квантовий оптимальний транспорт і слабкі топології», arXiv: 2306.12944, (2023).
Вищезазначені цитати від SAO / NASA ADS (останнє оновлення успішно 2023-10-16 14:47:44). Список може бути неповним, оскільки не всі видавці надають відповідні та повні дані про цитування.
Не вдалося отримати Перехресне посилання, наведене за даними під час останньої спроби 2023-10-16 14:47:42: Не вдалося отримати цитовані дані для 10.22331/q-2023-10-16-1143 з Crossref. Це нормально, якщо DOI був зареєстрований нещодавно.
Ця стаття опублікована в Quantum під Creative Commons Attribution 4.0 International (CC на 4.0) ліцензія. Авторське право залишається за оригінальними власниками авторських прав, такими як автори або їх установи.
- Розповсюдження контенту та PR на основі SEO. Отримайте посилення сьогодні.
- PlatoData.Network Vertical Generative Ai. Додайте собі сили. Доступ тут.
- PlatoAiStream. Web3 Intelligence. Розширення знань. Доступ тут.
- ПлатонЕСГ. вуглець, CleanTech, Енергія, Навколишнє середовище, Сонячна, Поводження з відходами. Доступ тут.
- PlatoHealth. Розвідка про біотехнології та клінічні випробування. Доступ тут.
- джерело: https://quantum-journal.org/papers/q-2023-10-16-1143/
- : має
- :є
- : ні
- ][стор
- $UP
- 003
- 07
- 1
- 10
- 100
- 102
- 107
- 11
- 110
- 116
- 118
- 12
- 125
- 13
- 14
- 15%
- 150
- 16
- 17
- 178
- 179
- 19
- 1994
- 1996
- 1998
- 1999
- 20
- 2001
- 2005
- 2006
- 2008
- 2010
- 2011
- 2012
- 2013
- 2014
- 2015
- 2016
- 2017
- 2018
- 2019
- 2020
- 2021
- 2022
- 2023
- 22
- 23
- 24
- 247
- 25
- 26
- 27
- 28
- 29
- 2D
- 30
- 31
- 32
- 33
- 35%
- 36
- 39
- 40
- 41
- 46
- 49
- 50
- 51
- 52
- 53
- 54
- 58
- 60
- 65
- 66
- 67
- 7
- 70
- 72
- 73
- 75
- 77
- 8
- 80
- 84
- 87
- 9
- 90
- 91
- 97
- 98
- a
- вище
- РЕЗЮМЕ
- академічний
- доступ
- активоване
- Адам
- Відрегульований
- аванси
- змагальність
- приналежності
- знову
- алгоритм
- ВСІ
- вже
- Також
- альтернатива
- завжди
- am
- Амстердам
- an
- аналіз
- та
- Ендрю
- Інший
- додаток
- застосування
- підхід
- ЕСТЬ
- Артур
- AS
- ашер
- аспекти
- Допомога
- At
- атом
- спроба
- автор
- authors
- доступний
- усереднення
- b
- Balance
- заснований
- BE
- стає
- було
- Берлін
- між
- пов'язаний
- Brain
- Перерва
- Будапешт
- Пакет
- by
- Кембридж
- CAN
- Може отримати
- carried
- випадок
- Центр
- центральний
- центр
- сертифікація
- канали
- охарактеризувати
- Чарлі
- більш дешевий
- Крістофер
- Міста
- Місто
- класифікація
- Collective
- Приходити
- ком
- коментар
- Commons
- повний
- складність
- комп'ютер
- Інформатика
- конференція
- З'єднуватися
- підключений
- будувати
- споживання
- містити
- зміст
- внески
- Зближення
- Опукла
- авторське право
- кореляції
- Відповідний
- Коштувати
- може
- копія
- країна
- курс
- Критерії
- Перетинати
- дані
- наука про дані
- Девід
- визначати
- певний
- затримка
- Це
- Щільність
- докладно
- виявляти
- Виявлення
- різний
- напрям
- розбрат
- обговорювати
- відстань
- розподіл
- Розподілу
- do
- управляти
- краплі
- під час
- e
- E&T
- кожен
- земля
- легко
- Економіка
- editors
- зусилля
- el
- Машинобудування
- однаково
- Так само
- рівняння
- Еріком
- по суті
- оцінити
- Оцінки
- Ефір (ETH)
- Навіть
- повсякденний
- досліджувати
- Вивчення
- Приклади
- Екзотичний
- очікувати
- експеримент
- продовжити
- сімей
- сім'я
- знаменитий
- далеко
- Федеріко
- поле
- Поля
- знайти
- виявлення
- потік
- для
- форма
- освіта
- знайдений
- фонд
- Підвалини
- чотири
- Рамки
- відвертий
- Безкоштовна
- від
- Паливо
- функція
- функціональний
- фундаментальний
- прогалини
- Gen
- Загальне
- генеративний
- генеративні змагальні мережі
- геометрія
- Жерар
- отримати
- графік
- Group
- Гарольд
- Гарвард
- Мати
- прихований
- Пагорби
- власники
- Головна
- Як
- HTML
- HTTP
- HTTPS
- i
- IEEE
- if
- ii
- зображення
- Класифікація зображень
- зображень
- картина
- Зображеннями
- Іман
- in
- Инк
- нерівності
- Нерівність
- інформація
- інформативний
- екземпляр
- Інститут
- установи
- цікавий
- Міжнародне покриття
- інтерпретація
- введені
- Вступ
- iOS
- IT
- ЙОГО
- сам
- січень
- JavaScript
- Джон
- журнал
- подорож
- поцілунок
- просто
- останній
- lawrence
- УЧИТЬСЯ
- вивчення
- Залишати
- читання
- Подветренний
- дозволяти
- li
- ліцензія
- життя
- МЕЖА
- рамки
- Лінія
- Рідина
- список
- місцевий
- подивитися
- від
- машина
- навчання за допомогою машини
- журнал
- управління
- керівництво
- багато
- карта
- карти
- Марко
- Маркус
- Мартін
- Маса
- Массачусетс
- маси
- математики
- математика
- Матриця
- макс-ширина
- Може..
- значити
- вимір
- вимірювання
- заходи
- механіка
- медичний
- Медична візуалізація
- згаданий
- метрика
- Метрика
- Метрологія
- може бути
- мінімізація
- змішаний
- модель
- моделювання
- Моделі
- Імпульс
- місяць
- більше
- Morgan
- рухатися
- переміщення
- таємничий
- Необхідність
- мереж
- Нейронний
- Нові
- Нью-Йорк
- наступний
- Нобелівський лауреат
- нормальний
- примітки
- поняття
- отриманий
- жовтень
- of
- on
- ONE
- відкрити
- операції
- оптика
- оптимальний
- оптимізація
- or
- порядок
- оригінал
- Інше
- наші
- з
- над
- Пабло
- пакет
- пакети
- сторінка
- сторінок
- пара
- Пол
- Папір
- Паріс
- Парк
- Пол
- персонал
- перспектива
- Пітер
- фаза
- ФІЛ
- Фізика
- місце
- plato
- Інформація про дані Платона
- PlatoData
- Play
- PO
- позитивний
- це можливо
- влада
- Точність
- представити
- press
- Принстон
- ймовірність
- Проблема
- ПРОЦ
- Праці
- процес
- процеси
- обробка
- програма
- Програмування
- прогрес
- властивості
- власність
- забезпечувати
- опублікований
- видавець
- видавців
- квадратичний
- в якості
- кількісний
- кількість
- Квантовий
- квантове заплутування
- квантова інформація
- Квантова механіка
- Квантова оптика
- квантова фізика
- квантові системи
- квантові технології
- Кубіт
- кубіти
- R
- ставки
- швидше
- реальний
- останній
- нещодавно
- посилання
- Відображає
- Незалежно
- режим
- зареєстрований
- пов'язаний
- відносини
- відносний
- залишається
- подання
- дослідження
- обмежити
- результати
- повернення
- огляд
- дорога
- Роланд
- Роль
- дах
- Рой
- Рояль
- s
- Сем
- Сан -
- ПІСНІТЬ
- say
- Школа
- SCI
- наука
- НАУКИ
- науковий
- Скотт
- здається
- сенс
- чутливий
- набори
- Форма
- siam
- Сигнал
- підпис
- косий
- невеликий
- solid
- Простір
- пробіли
- Спін
- standard
- стан
- Штати
- статистичний
- статистика
- Стівен
- більш сильний
- Вивчення
- Успішно
- такі
- підходящий
- сума
- система
- Systems
- T
- Taiwan
- Технологія
- розповідає
- шаблон
- Тестування
- Тести
- ніж
- Що
- Команда
- Графік
- їх
- теорія
- Ці
- вони
- це
- ті
- times
- назва
- до
- Інструменти
- Усього:
- trans
- Перетворення
- перевезення
- транспорт
- подорожувати
- Тенденції
- два
- кінцевий
- Невизначеність
- при
- що лежить в основі
- на жаль
- єдиний
- університет
- оновлений
- URL
- us
- використання
- звичайний
- варіації
- версія
- дуже
- через
- життєво важливий
- обсяг
- з
- W
- ван
- хотіти
- було
- шлях..
- we
- були
- коли
- Чи
- який
- в той час як
- ВООЗ
- Вільям
- Зима
- з
- Work
- світ
- X
- рік
- ще
- йорк
- зефірнет
- нуль
- Чжан