Ayrılabilir durumlar üzerinde bir optimizasyona dayalı Kuantum Wasserstein mesafesi

Ayrılabilir durumlar üzerinde bir optimizasyona dayalı Kuantum Wasserstein mesafesi

Zaman Damgası: 16 Ekim 2023 10:35
Kaynak Düğüm: 2938953

Géza Tóth1,2,3,4,5 ve József Pitrik5,6,7

1Teorik Fizik, Bask Ülkesi Üniversitesi UPV/EHU, ES-48080 Bilbao, İspanya
2EHU Quantum Center, Bask Ülkesi Üniversitesi UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscay, İspanya
3Donostia Uluslararası Fizik Merkezi (DIPC), ES-20080 San Sebastián, İspanya
4IKERBASQUE, Bask Bilim Vakfı, ES-48011 Bilbao, İspanya
5Katı Hal Fiziği ve Optik Enstitüsü, Wigner Fizik Araştırma Merkezi, HU-1525 Budapeşte, Macaristan
6Alfréd Rényi Matematik Enstitüsü, Reáltanoda u. 13-15., HU-1053 Budapeşte, Macaristan
7Analiz ve Yöneylem Araştırması Bölümü, Matematik Enstitüsü, Budapeşte Teknoloji ve Ekonomi Üniversitesi, Müegyetem rkp. 3., HU-1111 Budapeşte, Macaristan

Bu makaleyi ilginç mi buldunuz yoksa tartışmak mı istiyorsunuz? SciRate'e çığlık at veya yorum bırak.

Özet

Kuantum Wasserstein mesafesini, birleştirmenin optimizasyonu genel olarak iki parçalı kuantum durumları yerine iki parçalı ayrılabilir durumlar üzerinden gerçekleştirilecek şekilde tanımlıyoruz ve özelliklerini inceliyoruz. Şaşırtıcı bir şekilde, kişisel mesafenin kuantum Fisher bilgisiyle ilişkili olduğunu bulduk. Optimum iki parçalı ayrılabilir duruma karşılık gelen bir taşıma haritası sunuyoruz. Tanıtılan kuantum Wasserstein mesafesinin kuantum dolaşıklığı tespit eden kriterlerle nasıl bağlantılı olduğunu tartışıyoruz. Kuantum durumları üzerindeki minimizasyon yerine bir maksimizasyon koyarak, kuantum Wasserstein mesafesinden elde edilebilecek varyans benzeri nicelikleri tanımlarız. Sonuçlarımızı genelleştirilmiş kuantum Fisher bilgi miktarları ailesine genişletiyoruz.

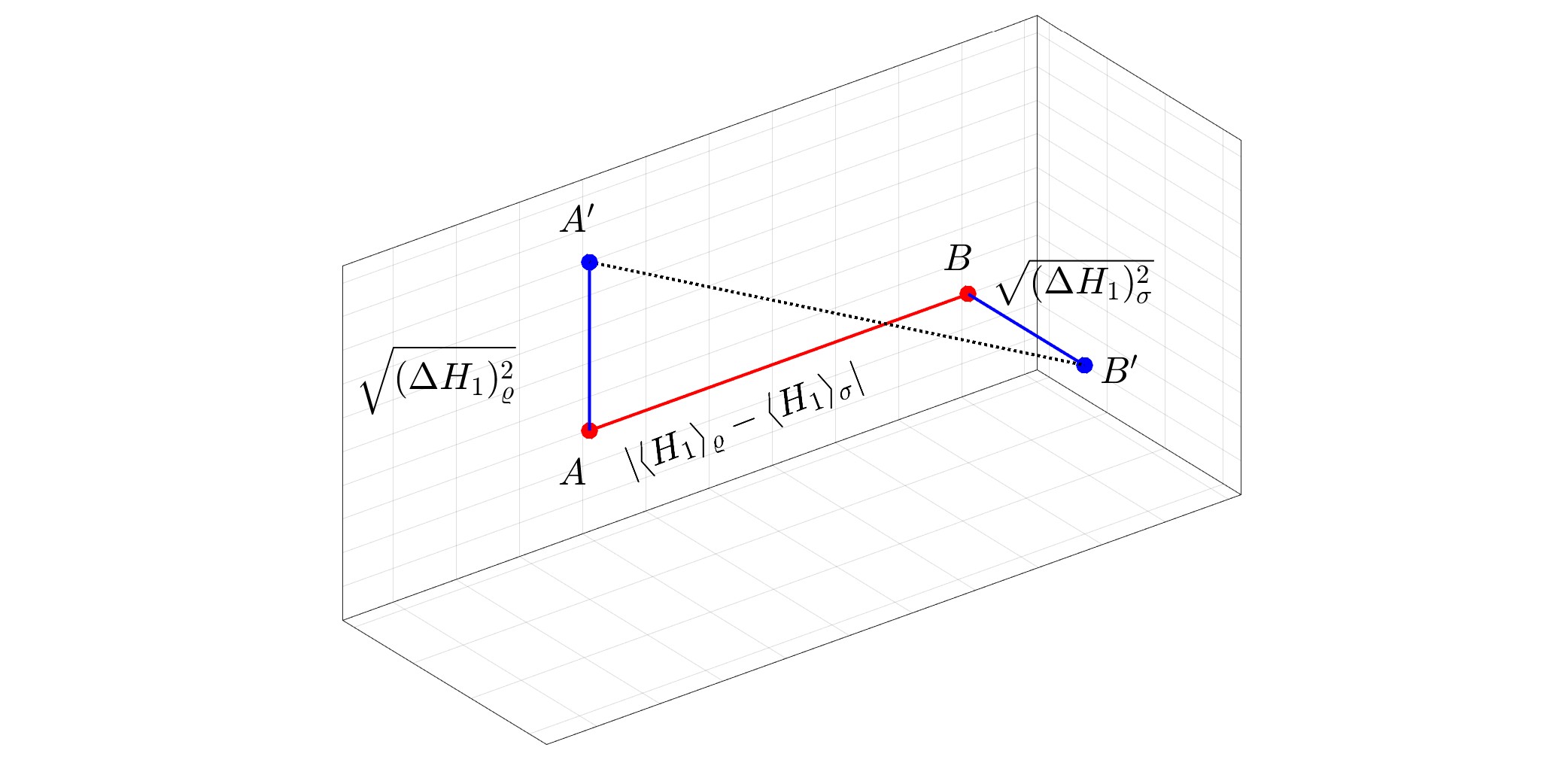
Öne çıkan görsel: $N=1.$ için saf durum $varrho$ ile karma durum $sigma$ arasındaki kuantum Wasserstein mesafesinin geometrik temsili. Kuantum Wasserstein mesafesi, $A'$ arasındaki olağan Öklid mesafesinin $1/sqrt2$ katına eşittir. ve $B'.$

Popüler özet

Günlük yaşamda iki şehrin mesafesi bize birinden diğerine kaç kilometre gitmemiz gerektiğini söyler. Bir şehirden diğerine ne kadar kolay gidebileceğimizi de yolculuğumuz sırasında yakıt tüketimini ölçerek karakterize etmek mümkündür. İkincisi, yolun topoğrafyasına bağlı olarak seyahatin maliyetini yansıtması açısından daha bilgilendiricidir; örneğin, temel alınan metriğe duyarlıdır. Daha sonra bir kum yığınını bir yerden başka bir yere taşımamız gerektiğini ve yeni yığının farklı bir formda olabileceğini düşünelim. Bu durumda yine kumun taşınması için harcanan çabayı nakliye maliyetiyle karakterize edebiliriz.

Mesafeler matematik, fizik ve mühendislikte merkezi bir rol oynar. Olasılık ve istatistikteki temel sorun, iki olasılık dağılımı arasındaki mesafeyi ölçen kullanışlı ölçümler bulmaktır. Ne yazık ki, olasılık dağılımları arasındaki mesafeye ilişkin pek çok kavram, örneğin p(x) ve q(x), eğer birbirleriyle örtüşmüyorlarsa maksimumdur, yani. örneğin, diğeri sıfır olmadığında biri her zaman sıfırdır. Bu, birçok uygulama için pratik değildir. Örneğin kum benzetmesine dönecek olursak, üst üste gelmeyen iki kum yığını, aralarındaki mesafenin 10 km ya da 100 km olmasına bakılmaksızın birbirine eşit uzaklıkta görünüyor. Optimal taşıma teorisi, olasılık dağılımları arasında Wasserstein mesafesi olarak adlandırılan alternatif bir mesafe kavramı oluşturmanın bir yoludur. Dağılımlar birbiriyle örtüşmese bile maksimum olmayabilir, temel ölçüte (yani taşıma maliyetine) duyarlıdır ve esasen birinden diğerine geçmek için ihtiyaç duyduğumuz çabayı ifade eder, sanki kum tepeleriymiş gibi.

Son zamanlarda kuantum Wasserstein mesafesi, klasik Wasserstein mesafesini genelleştirerek tanımlanmıştır. İki parçalı bir kuantum sisteminin kuantum durumları üzerindeki maliyet fonksiyonunun minimizasyonuna dayanmaktadır. Kuantum dünyasında yukarıda bahsettiğimiz özelliğe benzer bir özelliğe sahiptir. Dik durumlar için maksimum olmayabilir; bu, örneğin kuantum verilerini bir algoritmaya öğretmemiz gerektiğinde faydalıdır.

Bekleyebileceğimiz gibi kuantum Wasserstein mesafesinin klasik emsalinden çok farklı özellikleri de var. Örneğin bir kuantum durumunun kendisine olan uzaklığını ölçtüğümüzde sıfırdan farklı olabilir. Bu zaten kafa karıştırıcı olsa da, öz mesafenin, kuantum fiziğinin temellerine hayati katkıları olan Nobel ödüllü E. P. Wigner ve M. M. Yanase tarafından 1963 yılında ortaya atılan Wigner-Yanase çarpık bilgisiyle ilişkili olduğu da tespit edildi.

Makalemizde bu gizemli bulguya bir başka açıdan bakıyoruz. Yukarıda bahsedilen minimizasyon işlemini ayrılabilir durumlarla sınırlandırıyoruz. Bunlar dolaşıklık içermeyen kuantum halleridir. Öz mesafenin, kuantum metrolojisinde ve kuantum tahmin teorisinde merkezi bir nicelik olan ve örneğin ünlü Cramer-Rao sınırında ortaya çıkan kuantum Fisher bilgisi haline geldiğini bulduk. Böyle bir Wasserstein mesafesinin özelliklerini inceleyerek çalışmamız, kuantum Wasserstein mesafesi teorisini kuantum dolaşıklık teorisine bağlamanın yolunu açıyor.

► BibTeX verileri

► Referanslar

[1] G. Monge. "Mémoire sur la theory des déblais et des remblais". Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L. Kantorovitch. “Kitlelerin yer değiştirmesi üzerine”. Yönetim Bilimi 5, 1–4 (1958). URL: http://​/​www.jstor.org/​stable/​2626967.
http: / / www.jstor.org/ kararlı / 2626967

[3] Emmanuel Boissard, Thibaut Le Gouic ve Jean-Michel Loubes. “Wasserstein metrikleriyle dağıtımın şablon tahmini”. Bernoulli 21, 740–759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

[4] Oleg Butkovski. "Wasserstein metriğinde Markov süreçlerinin subgeometrik yakınsama oranları". Ann. Başvuru Muhtemelen. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[5] M. Hairer, J.-C. Mattingly ve M. Scheutzow. “Asimptotik eşleşme ve Harris teoreminin stokastik gecikme denklemlerine uygulamaları ile genel bir formu”. Muhtemelen. Teori İlişkisi. Alanlar 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[6] M. Hairer ve JC Mattingly. “Wasserstein Uzaklıklarındaki Spektral Boşluklar ve 2B Stokastik Navier-Stokes Denklemleri”. Ann. Muhtemelen. 36, 2050–2091 (2008).
https:/​/​doi.org/10.1214/​08-AOP392

[7] A. Figalli, F. Maggi ve A. Pratelli. “Niceliksel izoperimetrik eşitsizliklere toplu taşıma yaklaşımı”. İcat etmek. Matematik. 182, 167–211. (2010).
HTTPS: / / doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli ve F. Maggi. "Küçük kütle rejiminde sıvı damlaların ve kristallerin şekli üzerine". Arch. Rasyon. Mekanik Anal. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[9] J. Lott ve C. Villani. "Optimum taşıma yoluyla metrik ölçü uzayları için Ricci eğriliği". Ann. Matematik. 169 (3), 903–991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

[10] Max-K. von Renesse ve Karl-Theodor Sturm. "Ulaşım eşitsizlikleri, gradyan tahminleri, entropi ve Ricci eğriliği". İletişim Saf Uygulama Matematik. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[11] Karl-Theodor Sturm. “Metrik ölçü uzaylarının geometrisi üzerine I”. Acta Matematik. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[12] Karl-Theodor Sturm. “Metrik ölçü uzaylarının geometrisi üzerine II”. Acta Matematik. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[13] Benoıt Kloeckner. "Wasserstein uzaylarının geometrik bir çalışması: Öklid uzayları". Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03

[14] György Pál Gehér, Tamás Titkos ve Dániel Virosztek. "Wasserstein uzaylarının izometrik gömülmeleri üzerine - ayrık durum". J. Matematik. Anal. Başvuru 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. "Wasserstein uzaylarının izometrik çalışması - gerçek çizgi". Trans. Amer. Matematik. Sos. 373, 5855–5883 (2020).
https://​/​doi.org/​10.1090/​tran/​8113

[16] György Pál Gehér, Tamás Titkos ve Dániel Virosztek. "Wasserstein uzaylarının izometri grubu: Hilbert durumu". J. Lond. Matematik. Sos. 106, 3865–3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

[17] György Pál Gehér, Tamás Titkos ve Dániel Virosztek. "Wasserstein tori ve kürelerin izometrik sertliği". Mathematika 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[18] Gergely Kiss ve Tamás Titkos. "Wasserstein uzaylarının izometrik katılığı: Grafik metrik durumu". Proc. Am. Matematik. Sos. 150, 4083–4097 (2022).
https://​/​doi.org/​10.1090/​proc/​15977

[19] György Pál Gehér, Tamás Titkos ve Dániel Virosztek. "İkinci dereceden Wasserstein uzayının gerçek çizgi üzerindeki egzotik izometri akışı üzerine". Lineer Cebir Uyg. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, SR Park ve GK Rohde. "Radon kümülatif dağılım dönüşümü ve görüntü sınıflandırmasına uygulanması". IEEE Çev. Görüntü Süreci. 25, 920–934 (2016).
https:/​/​doi.org/10.1109/​TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek ve GK Rohde. "Görüntü kümelerindeki farklılıkları ölçmek ve görselleştirmek için doğrusal bir optimal taşıma çerçevesi". Uluslararası J. Bilgisayar. Vis. 101, 254–269 (2013).
HTTPS: / / doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. “Optimal Kütle Taşıma: Sinyal işleme ve makine öğrenme uygulamaları”. IEEE Sinyal İşleme Dergisi 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

[23] A. Gramfort, G. Peyré ve M. Cuturi. “Nöro Görüntüleme Verilerinin Hızlı Optimal Aktarım Ortalaması”. Tıbbi Görüntülemede Bilgi İşleme. IPMI 2015. Bilgisayar Bilimleri Ders Notları 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu ve X. Gu. "Beyin morfometri analizi için Wasserstein mesafesini kullanarak şekil sınıflandırması". Tıbbi Görüntülemede Bilgi İşleme. IPMI 2015. Bilgisayar Bilimleri Ders Notları 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala ve Léon Bottou. "Wasserstein üretken düşman ağları". Doina Precup ve Yee Whye Teh, editörler, 34. Uluslararası Makine Öğrenimi Konferansı Bildirileri. Makine Öğrenimi Araştırması Bildirileri Cilt 70, sayfalar 214-223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] TA El Moselhy ve YM Marzouk. "Optimal haritalarla Bayes çıkarımı". J. Bilgisayar. Fizik. 231, 7815–7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022

[27] Gabriel Peyré ve Marco Cuturi. “Hesaplamalı Optimal Taşıma: Veri Bilimine Uygulamalarla”. Kurmak. Trendler Makine Öğrenimi. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya ve Tomaso A Poggio. "Wasserstein kaybıyla öğrenme". C. Cortes, N. Lawrence, D. Lee, M. Sugiyama ve R. Garnett, editörler, Advances in Neural Information Processing Systems. Cilt 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[29] A. Ramdas, NG Trillos ve M. Cuturi. “Wasserstein İki Örneklem Testi ve İlgili Parametrik Olmayan Test Aileleri Üzerine”. Entropi 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[30] S. Srivastava, C. Li ve DB Dunson. “Wasserstein Uzayında Barycenter aracılığıyla Ölçeklenebilir Bayes”. J. Mach. Öğrenmek. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski ve Wojeciech Slomczynski. “Kuantum durumları arasındaki Monge mesafesi”. J. Phys. C: Matematik. Gen. 31, 9095–9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[32] Karol Życzkowski ve Wojciech Slomczynski. “Kuantum durumlarının küresi ve geometrisine ilişkin Monge metriği”. J. Phys. C: Matematik. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[33] Ingemar Bengtsson ve Karol Życzkowski. "Kuantum durumlarının geometrisi: Kuantum dolaşıklığına giriş". Cambridge Üniversitesi Yayınları. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane ve D. Voiculescu. "İz durumu uzayında Wasserstein metriğinin serbest olasılık analoğu". GAFA, Geom. Fonksiyon Anal. 11, 1125–1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[35] Eric A. Carlen ve Jan Maas. "Fermiyonik Fokker-Planck Denkleminin Entropi için Gradyan Akış Olduğu Değişmez Olasılıkta 2-Wasserstein Metriğinin Bir Analogu". İletişim Matematik. Fizik. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[36] Eric A. Carlen ve Jan Maas. "Ayrıntılı denge ile kuantum Markov yarı grupları için gradyan akışı ve entropi eşitsizlikleri". J. Fonksiyon. Anal. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

[37] Eric A. Carlen ve Jan Maas. "Değişmeli olmayan analiz, optimal taşıma ve enerji tüketen kuantum sistemlerinde fonksiyonel eşitsizlikler". J. Stat. Fizik. 178, 319–378 (2020).
HTTPS: / / doi.org/ 10.1007 / s10955-019-02434-w

[38] Nilanjana Datta ve Cambyse Rouzé. "Kuantum fonksiyonel ve taşıma maliyeti eşitsizliklerinden kuantum durumlarının konsantrasyonu". J. Matematik. Fizik. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[39] Nilanjana Datta ve Cambyse Rouzé. "Göreceli entropi, optimal taşıma ve Fisher bilgisinin ilişkilendirilmesi: Bir kuantum HWI eşitsizliği". Ann. Henri Poincaré 21, 2115–2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[40] François Golse, Clément Mouhot ve Thierry Paul. "Kuantum mekaniğinin ortalama alanı ve klasik sınırları üzerine". İletişim Matematik. Fizik. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[41] François Golse ve Thierry Paul. “Ortalama alan ve yarı klasik rejimde Schrödinger denklemi”. Arch. Rasyon. Mekanik Anal. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[42] François Golse ve Thierry Paul. "Dalga paketleri ve kuantum mekaniğinde ikinci dereceden Monge-Kantorovich mesafesi". Rendus Math'ı hesaplar. 356, 177–197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

[43] François Golse. “Ortalama alan ve yarı klasik rejimde kuantum $N$-cisim problemi”. Phil. Trans. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse ve T. Paul. “Kuantum optimal taşıma daha ucuzdur”. J. Stat. Fizik. 181, 149–162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[45] Emanuele Caglioti, François Golse ve Thierry Paul. "Kuantum yoğunlukları için optimal taşınmaya doğru". arXiv:2101.03256 (2021).
https:/​/​doi.org/10.48550/​arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma ve Dario Trevisan. "Kuantum kanallarıyla kuantum optimal taşıma". Ann. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan ve Seth Lloyd. “1. dereceden kuantum Wasserstein mesafesi”. IEEE Çev. Enf. Teori 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole ve Karol Życzkowski. “Kuantum Monge-Kantorovich problemi ve yoğunluk matrisleri arasındaki taşıma mesafesi”. Fizik. Rahip Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland ve Karol Życzkowski. "Kuantum optimal taşıma". arXiv:2105.06922 (2021).
https:/​/​doi.org/10.48550/​arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein ve K. Życzkowski. "Kuantum 2-Wasserstein mesafesinin monotonluğu". J. Phys. C: Matematik. Teori. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos ve Dániel Virosztek. "Kubit durum uzayında Kuantum Wasserstein izometrileri". J. Matematik. Anal. Başvuru 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe ve Seth Lloyd. "Kuantum Devrelerinin Wasserstein Karmaşıklığı". arXiv: 2208.06306 (2022).
https:/​/​doi.org/10.48550/​arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu ve Seth Lloyd. “Kuantum dünya taşıyıcısının mesafesiyle kuantum verilerini öğrenme”. Kuantum Bilimi. Teknoloji. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[54] EP Wigner ve Mutsuo M. Yanase. “Dağıtımların bilgi içerikleri”. Proc. Natl. Acad. Bilim. ABD 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki ve Karol Horodecki. "Kuantum dolaşıklığı". Mod. fizik 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[56] Otfried Gühne ve Géza Tóth. "Dolaşıklık tespiti". fizik 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik ve Marcus Huber. "Teoriden deneye dolaşıklık sertifikası". Nat. Rahip Phys. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd ve Lorenzo Maccone. "Kuantumla geliştirilmiş ölçümler: Standart kuantum sınırını aşmak". Bilim 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

[59] Matteo GA Paris. “Kuantum teknolojisi için kuantum tahmini”. Uluslararası J. Quant. Enf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna ve Jan Kolodynski. “Dördüncü Bölüm – Optik interferometride kuantum sınırları”. Prog. Optik 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze ve Augusto Smerzi. “Faz tahmininin kuantum teorisi”. GM Tino ve MA Kasevich, editörler, Atom İnterferometrisi (Proc. Int. School of Physics 'Enrico Fermi', Course 188, Varenna). Sayfalar 691–741. IOS Press, Amsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Géza Tóth ve Dénes Petz. "Varyansın ekstrem özellikleri ve kuantum Fisher bilgisi". Fizik. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[63] Sixia Yu. “Dışbükey Varyans Çatısı Olarak Kuantum Fisher Bilgisi”. arXiv:1302.5311 (2013).
https:/​/​doi.org/10.48550/​arXiv.1302.5311
arXiv: 1302.5311

[64] Géza Tóth ve Florian Fröwis. "Yoğunluk matrislerinin dışbükey ayrışmalarına dayanan varyans ve kuantum Fisher bilgisiyle belirsizlik ilişkileri". Fizik. Rev. Araştırma 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[65] Shao-Hen Chiew ve Manuel Gessner. “Kuantum Fisher bilgisi ile toplam belirsizlik ilişkilerinin iyileştirilmesi”. Fizik. Rev. Araştırma 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[66] CW Helstrom. “Kuantum algılama ve tahmin teorisi”. Akademik Basın, New York. (1976). URL: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[67] AS Holevo. “Kuantum teorisinin olasılıksal ve istatistiksel yönleri”. Kuzey Hollanda, Amsterdam. (1982).

[68] Samuel L. Braunstein ve Carlton M. Caves. "İstatistiksel mesafe ve kuantum durumlarının geometrisi". fizik Rahip Lett. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

[69] Samuel L Braunstein, Carlton M Caves ve Gerard J Milburn. "Genelleştirilmiş belirsizlik ilişkileri: Teori, örnekler ve Lorentz değişmezliği". Ann. Fizik. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[70] Denes Petz. “Kuantum bilgi teorisi ve kuantum istatistikleri”. Springer, Berlin, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[71] Géza Tóth ve Iagoba Apellaniz. "Kuantum bilgi bilimi perspektifinden kuantum metrolojisi". J. Phys. C: Matematik. teori 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied ve Philipp Treutlein. "Atomik toplulukların klasik olmayan durumlarıyla kuantum metrolojisi". Mod. fizik 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[73] Marco Barbieri. “Optik kuantum metrolojisi”. PRX Kuantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

[74] Zoltán Léka ve Dénes Petz. "Matris varyanslarının bazı ayrıştırmaları". Muhtemelen. Matematik. Devletçi. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Dénes Petz ve Dániel Virosztek. "Matris varyansları için bir karakterizasyon teoremi". Acta Sci. Matematik. (Szeged) 80, 681–687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

[76] Akio Fujiwara ve Hiroshi Imai. "Kuantum kanallarının manifoldları üzerinde bir fiber demeti ve bunun kuantum istatistiklerine uygulanması". J. Phys. C: Matematik. Teori. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[77] BM Escher, RL de Matos Filho ve L. Davidovich. "Gürültülü kuantumla geliştirilmiş metrolojide nihai hassasiyet sınırını tahmin etmek için genel çerçeve". Nat. Fizik. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński ve Mădălin Guţă. "Kuantumla geliştirilmiş metrolojide anlaşılması zor Heisenberg sınırı". Nat. İletişim 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[79] Iman Marvian. "Kuantum termodinamiğinde kuantum avcısı bilgilerinin operasyonel yorumlanması". Fizik. Rahip Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

[80] Reinhard F. Werner. "Kuantum, gizli değişkenli bir modeli kabul eden Einstein-Podolsky-Rosen korelasyonlarıyla durumları". Fizik. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss ve M. Lewenstein. "Ayırt edilemeyen parçacık sistemlerinde kuantum korelasyonları". Ann. Fizik. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui ve Nobuhiro Yonezawa. "Değişim simetrisi ve çok parçalı dolaşma". Fizik. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[83] Pawel Horodecki. “Ayrılabilirlik kriteri ve pozitif kısmi aktarımla ayrılamaz karışık durumlar”. Fizik. Lett. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[84] Asher Peres. "Yoğunluk matrisleri için ayrılabilirlik kriteri". Fizik Rev. Lett. 77, 1413–1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki ve Ryszard Horodecki. "Bağlı dolaşma etkinleştirilebilir". Fizik. Rahip Lett. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

[86] Géza Tóth ve Tamás Vértesi. "Pozitif kısmi devrikliğe sahip kuantum durumları metroloji için faydalıdır". Fizik. Rahip Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

[87] Scott Hill ve William K. Wootters. “Bir çift kuantum bitinin dolaşması”. Fizik. Rahip Lett. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

[88] William K. Wootters. "İki kübitlik keyfi bir durumun oluşumunun dolaşıklığı". fizik Rahip Lett. 80, 2245–2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal ve Armin Uhlmann. “Yardım karışıklığı”. nicem-ph/​9803033 (1998).
https:/​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: kuant-ph / 9803033

[90] John A. Smolin, Frank Verstraete ve Andreas Winter. “Yardımın dolaşması ve çok parçalı durum damıtma”. Fizik. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[91] Holger F. Hofmann ve Shigeki Takeuchi. “Dolaşıklığın işareti olarak yerel belirsizlik ilişkilerinin ihlali”. Fizik. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[92] Otfried Gühne. "Dolaşıklığın belirsizlik ilişkileri yoluyla karakterize edilmesi". Fizik. Rahip Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth ve Peter Adam. “Yerel belirsizlik ilişkilerine dayalı dolaşma kriterleri, hesaplanabilir çapraz norm kriterlerinden kesinlikle daha güçlüdür”. Fizik. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza ve Géza Tóth. "Keyfi dönüş için sıkma eşitsizlikleri". fizik Rahip Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

[95] AR Edmonds. "Kuantum mekaniğinde açısal momentum". Princeton Üniversitesi Yayınları. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[96] Géza Tóth. "Kolektif ölçümlerle bozonik atomların optik kafeslerinde dolaşıklık tespiti". fizik A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne ve Hans J. Briegel. "Optimal döndürme sıkma eşitsizlikleri, döndürme modellerinde bağlı karışıklığı algılar". fizik Rahip Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

[98] Géza Tóth ve Morgan W. Mitchell. "Atom topluluklarında makroskobik singlet durumların oluşturulması". Yeni J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[99] Géza Tóth. "Simetrik Dicke durumları çevresinde çok parçalı dolaşıklığın tespiti". J. Opt. Sos. Am. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

[100] Géza Tóth, Tobias Moroder ve Otfried Gühne. “Dışbükey çatı dolaşma önlemlerinin değerlendirilmesi”. Fizik. Rahip Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

[101] Lieven Vandenberghe ve Stephen Boyd. “Yarı kesin programlama”. SIAM İncelemesi 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[102] Géza Tóth. "Çok parçalı dolaşıklık ve yüksek hassasiyetli metroloji". fizik A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé ve Augusto Smerzi. "Fisher bilgisi ve çoklu parçacık dolaşıklığı". fizik A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki ve Ryszard Horodecki. “Gizli metrolojik kullanışlılığın etkinleştirilmesi”. Fizik. Rahip Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo ve Federico M. Spedalieri. “Ayrılabilir ve dolaşmış durumları ayırt etmek”. Fizik. Rahip Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo ve Federico M. Spedalieri. “Ayrılabilirlik kriterlerinin tam ailesi”. Fizik. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo ve Federico M. Spedalieri. “Çok parçalı dolaşıklığın tespiti”. Fizik. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[108] Harold Ollivier ve Wojciech H. Zurek. "Kuantum uyumsuzluğu: Korelasyonların kuantumluğunun bir ölçüsü". fizik Rahip Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

[109] L. Henderson ve V. Vedral. “Klasik, kuantum ve toplam korelasyonlar”. J. Phys. C: Matematik. Gen. 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) ve Ujjwal Sen. "Kuantum anlaşmazlığı ve müttefikleri: son gelişmelerin gözden geçirilmesi". Temsilci Prog. Fizik. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

[111] Denes Petz. “Kuantum mekaniğinde Kovaryans ve Fisher bilgisi”. J. Phys. C: Matematik. Gen. 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[112] Paolo Gibilisco, Fumio Hiai ve Dénes Petz. "Kuantum kovaryansı, kuantum Fisher bilgisi ve belirsizlik ilişkileri". IEEE Çev. Enf. Teori 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[113] D. Petz ve C. Ghinea. “Kuantum Fisher bilgisine giriş”. Cilt 27, sayfalar 261–281. Dünya Bilimsel. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[114] Frank Hansen. “Metrik ayarlı eğrilik bilgisi”. Proc. Natl. Acad. Bilim. ABD 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami ve Frank Hansen. "Metrik ayarlı çarpık bilgilerle yerel kuantum belirsizliğine ve interferometrik güce birleşik bir yaklaşım". Entropi 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[116] MATLAB. “9.9.0.1524771(r2020b)”. MathWorks Inc. Natick, Massachusetts (2020).

[117] MOSEK ApS. “MATLAB kılavuzu için MOSK optimizasyon araç kutusu. Sürüm 9.0”. (2019). URL: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[118] J. Löfberg. “YALMIP: MATLAB'da Modelleme ve Optimizasyon için Bir Araç Kutusu”. CACSD Konferansı Bildirileri içinde. Taipei, Tayvan (2004).

[119] Géza Tóth. “QUBIT4MATLAB V3.0: MATLAB için kuantum bilgi bilimi ve kuantum optiği için bir program paketi”. Hesapla. Fizik. İletişim 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[120] QUBIT4MATLAB paketine https://​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433 adresinden ve https://​/​gtoth.eu/​qubit4matlab.html kişisel ana sayfasından ulaşılabilir.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Alıntılama

[1] Laurent Lafleche, “Kuantum Optimal Taşıma ve Zayıf Topolojiler”, arXiv: 2306.12944, (2023).

Yukarıdaki alıntılar SAO / NASA REKLAMLARI (son başarıyla 2023-10-16 14:47:44) güncellendi. Tüm yayıncılar uygun ve eksiksiz alıntı verisi sağlamadığından liste eksik olabilir.

Getirilemedi Alıntılanan veriler son girişim sırasında 2023-10-16 14:47:42: Crossref'ten 10.22331 / q-2023-10-16-1143 için belirtilen veriler getirilemedi. DOI yakın zamanda kaydedildiyse bu normaldir.

Bu Makale, Quantum'da Creative Commons Atıf 4.0 Uluslararası (CC BY 4.0) lisans. Telif hakkı, yazarlar veya kurumları gibi orijinal telif hakkı sahiplerine aittir.

Zaman Damgası:

Den fazla Kuantum Günlüğü