[Зеркало] Программы квадратичной арифметики: от нуля до героя

Виталик Бутерин через Блог Виталика Бутерина

Это зеркало поста на https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

В последнее время наблюдается большой интерес к технологии, лежащей в основе zk-SNARK, и люди все чаще пытаюсь демистифицировать то, что многие стали называть «лунной математикой» из-за ее явной не поддающейся расшифровке сложности. zk-SNARK действительно довольно сложно понять, особенно из-за огромного количества движущихся частей, которые должны собраться вместе, чтобы все это работало, но если мы разложим технологию по частям, то понять ее станет проще.

Целью этого поста не является полное введение в zk-SNARK; в качестве базовых знаний он предполагает, что (i) вы знаете, что такое zk-SNARK и что они делают, и (ii) знаете достаточно математики, чтобы рассуждать о таких вещах, как полиномы (если утверждение �(��)+��(��) =(��+��)(��) , где � и � — полиномы, вам кажется естественным и очевидным, значит, вы на правильном уровне). Скорее, пост углубляется в механизм, лежащий в основе технологии, и пытается как можно лучше объяснить первую половину конвейера, как это нарисовано исследователем zk-SNARK Эраном Тромером здесь:

Шаги здесь можно разделить на две половины. Во-первых, zk-SNARK нельзя напрямую применить к какой-либо вычислительной задаче; скорее, вам нужно преобразовать проблему в правильную «форму», чтобы проблема могла работать. Эта форма называется «программой квадратичной арифметики» (QAP), и преобразование кода функции в одну из них само по себе весьма нетривиально. Наряду с процессом преобразования кода функции в QAP есть еще один процесс, который можно запустить параллельно, чтобы, если у вас есть входные данные для кода, вы могли создать соответствующее решение (иногда называемое «свидетелем» QAP). После этого существует еще один довольно сложный процесс создания фактического «доказательства с нулевым разглашением» для этого свидетеля и отдельный процесс проверки доказательства, которое кто-то другой передает вам, но это детали, которые выходят за рамки этого поста. .

Пример, который мы выберем, прост: докажите, что вы знаете решение кубического уравнения: �3+�+5=35 (подсказка: ответ — 3). Эта проблема достаточно проста, чтобы результирующий QAP не был настолько большим, чтобы пугать, но и достаточно нетривиален, чтобы вы могли видеть, как в игру вступают все механизмы.

Запишем нашу функцию следующим образом:

def qeval(x):
    y = x**3
    return x + y + 5

Простой язык программирования специального назначения, который мы здесь используем, поддерживает базовую арифметику (+, −, ⋅, /), возведение в степень в постоянной степени (��7, но не ��) и присваивание переменных, что достаточно мощно, чтобы вы могли теоретически это сделать. любые вычисления внутри него (при условии, что количество вычислительных шагов ограничено; циклы не допускаются). Обратите внимание, что операторы по модулю (%) и сравнения (<, >, ≤, ≥) НЕ поддерживаются, так как не существует эффективного способа выполнения по модулю или сравнения непосредственно в арифметике конечных циклических групп (будьте благодарны за это; если бы был способ если сделать любой из них, то криптография на эллиптических кривых будет взломана быстрее, чем вы сможете произнести «двоичный поиск» и «китайскую теорему об остатках»).

Вы можете расширить язык до модулей и сравнений, предоставляя битовые разложения (например, 13=23+22+1) в качестве вспомогательных входных данных, доказывая правильность этих разложений и выполняя математические операции в двоичных схемах; в арифметике с конечными полями проверка на равенство (==) также возможна и на самом деле немного проще, но обе эти детали мы сейчас не будем вдаваться в подробности. Мы можем расширить язык для поддержки условных операторов (например, if �<5:��=7; else: �=9), преобразовав их в арифметическую форму: �=7⋅(��<5)+9⋅(��≥5 ), однако обратите внимание, что оба «пути» условного оператора должны быть выполнены, и если у вас много вложенных условных операторов, это может привести к большим накладным расходам.

Давайте теперь пройдемся по этому процессу шаг за шагом. Если вы хотите сделать это самостоятельно для какого-либо фрагмента кода, я здесь реализован компилятор (только для образовательных целей; пока не готов к созданию QAP для реальных zk-SNARK!).

уплощение

Первым шагом является процедура «сглаживания», при которой исходный код, который может содержать сколь угодно сложные операторы и выражения, преобразуется в последовательность операторов двух форм: ��=�� (где �� может быть переменной или числом ) и ��=�� (��) � (где �� могут быть +, −, ⋅, /, а �� и �� могут быть переменными, числами или самими подвыражениями). Вы можете думать о каждом из этих утверждений как о чем-то вроде логических элементов в схеме. Результат процесса выравнивания приведенного выше кода выглядит следующим образом:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

Если вы прочитаете исходный код и приведенный здесь код, вы легко увидите, что они эквивалентны.

Ворота в R1CS

Теперь мы преобразуем это в нечто, называемое системой ограничений ранга 1 (R1CS). R1CS – это последовательность групп трех векторов (��, �, �), а решением R1CS является вектор �, где � должно удовлетворять уравнению �.�⋅�.�−�.�=0, где . представляет собой скалярное произведение – проще говоря, если мы «сцепим» � и �, умножив два значения в одних и тех же позициях, а затем возьмем сумму этих произведений, затем проделаем то же самое с � и �, а затем � и � , то третий результат равен произведению первых двух результатов. Например, это удовлетворенный R1CS:

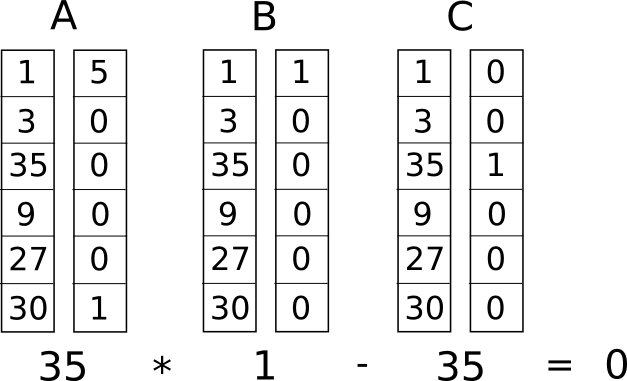
Но вместо одного ограничения у нас будет много ограничений: по одному на каждый логический элемент. Существует стандартный способ преобразования логического элемента в тройку (��,��,��) в зависимости от того, какая операция (+, −, ⋅ или /) и являются ли аргументы переменными или числами. Длина каждого вектора равна общему количеству переменных в системе, включая фиктивную переменную ~одну с первым индексом, представляющую число 1, входные переменные, фиктивную переменную ~out, представляющую выходные данные, а затем все промежуточные переменные (��1 и ��2 выше); векторы, как правило, будут очень редкими, заполняя только слоты, соответствующие переменным, на которые влияет какой-то конкретный логический элемент.

Сначала мы предоставим сопоставление переменных, которое будем использовать:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

Вектор решения будет состоять из назначений для всех этих переменных в указанном порядке.

Теперь мы дадим тройку (��,�,�) для первых ворот:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

Вы можете видеть, что если вектор решения содержит 3 во второй позиции и 9 в четвертой позиции, то независимо от остального содержимого вектора решения проверка скалярного произведения сведется к 3⋅3=9, и так что это пройдет. Если вектор решения имеет -3 во второй позиции и 9 в четвертой позиции, проверка также пройдет; Фактически, если вектор решения имеет 7 во второй позиции и 49 в четвертой позиции, то эта проверка все равно пройдет — цель этой первой проверки — проверить согласованность входных и выходных данных только первого вентиля.

Теперь перейдем ко вторым воротам:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

По аналогии с первой проверкой скалярного произведения здесь мы проверяем, что ��1⋅�=��.

Теперь третьи ворота:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

Здесь схема несколько иная: первый элемент вектора решения умножается на второй элемент, затем на пятый элемент, складываются два результата и проверяется, равна ли сумма шестому элементу. Поскольку первый элемент в векторе решения всегда равен единице, это всего лишь проверка сложения, проверяющая, что выходные данные равны сумме двух входных данных.

Наконец, четвёртые ворота:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

Здесь мы оцениваем последнюю проверку ~out =����2+5. Проверка скалярного произведения заключается в том, что мы берем шестой элемент в векторе решения, добавляем пять раз первый элемент (напоминание: первый элемент равен 1, поэтому это фактически означает добавление 5) и сравниваем его с третьим элементом, где мы сохраните выходную переменную.

И вот у нас есть R1CS с четырьмя ограничениями. Свидетель — это просто присвоение всем переменным, включая входные, выходные и внутренние переменные:

[1, 3, 35, 9, 27, 30]

Вы можете вычислить это самостоятельно, просто «выполнив» приведенный выше упрощенный код, начав с присвоения входной переменной = 3 и вводя значения всех промежуточных переменных и выходных данных по мере их вычисления.

Полный комплект R1CS представляет собой:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS в QAP

Следующий шаг — взять этот R1CS и преобразовать его в форму QAP, которая реализует ту же логику, за исключением использования полиномов вместо скалярных произведений. Мы делаем это следующим образом. Мы переходим от четырех групп по три вектора длины шесть к шести группам по три полинома степени 3, где оценивая полиномы в каждом координата х представляет собой одно из ограничений. То есть, если мы оцениваем полиномы при =1, мы получаем наш первый набор векторов, если мы оцениваем полиномы при =2, то мы получаем второй набор векторов и так далее.

Мы можем выполнить это преобразование, используя нечто, называемое Интерполяция Лагранжа. Проблема, которую решает интерполяция Лагранжа, заключается в следующем: если у вас есть набор точек (т.е. (��,��) пары координат), то выполнение интерполяции Лагранжа в этих точках дает вам полином, который проходит через все эти точки. Мы делаем это путем декомпозиции задачи: для каждой координаты мы создаем многочлен, который имеет желаемую координату в этой координате и координату 0 во всех других координатах, которые нас интересуют, а затем, чтобы получить окончательный результат В результате мы сложим все полиномы вместе.

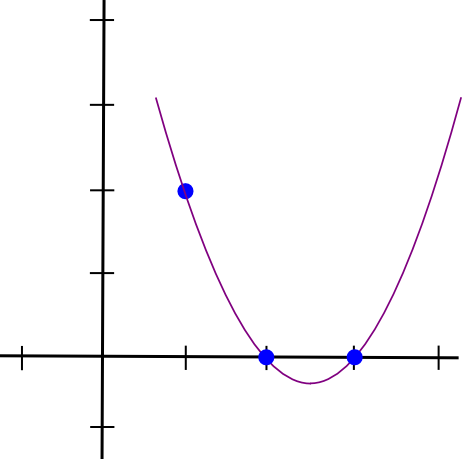
Давайте сделаем пример. Предположим, что нам нужен полином, который проходит через (1,3), (2,2) и (3,4). Мы начнем с создания полинома, который проходит через (1,3), (2,0) и (3,0). Как оказывается, создать полином, который «выступает» в точке = 1 и равен нулю в других интересующих точках, легко; мы просто делаем:

(x - 2) * (x - 3)

Это выглядит так:

Теперь нам просто нужно «изменить масштаб» так, чтобы высота в точке x=1 была правильной:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

Это дает нам:

1.5 * x**2 - 7.5 * x + 9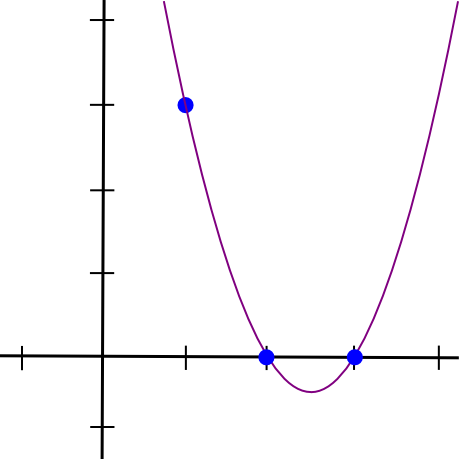

Затем мы делаем то же самое с двумя другими точками и получаем еще два полинома, похожих на них, за исключением того, что они «выступают» в точках =2 и =3 вместо =1. Складываем все три вместе и получаем:

1.5 * x**2 - 5.5 * x + 7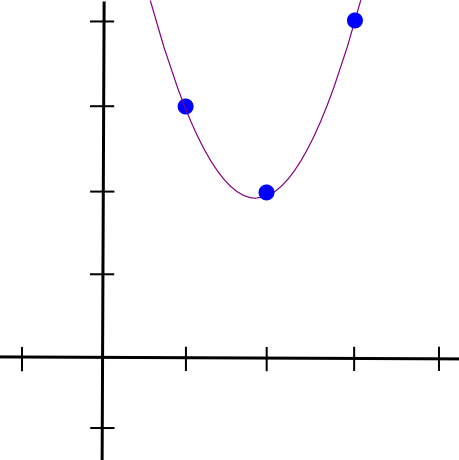

С именно теми координатами, которые нам нужны. Описанный выше алгоритм требует �(��3) времени, так как имеется � точек, и каждая точка требует �(��2) времени для умножения полиномов вместе; немного подумав, это можно сократить до ��(��2) времени, а еще подумав, используя алгоритмы быстрого преобразования Фурье и т.п., его можно сократить еще больше – решающая оптимизация, когда функции, которые используются в zk -На практике СНАРКи часто имеют многие тысячи ворот.

Теперь давайте воспользуемся интерполяцией Лагранжа, чтобы преобразовать нашу R1CS. Что мы собираемся сделать, так это взять первое значение из каждого вектора �, использовать интерполяцию Лагранжа, чтобы получить из него полином (при этом вычисление многочлена в � дает вам первое значение вектора �-го �), повторить процесс для первого значения каждого вектора � и �, а затем повторите этот процесс для вторых значений, третьего значения и так далее. Для удобства приведу ответы прямо сейчас:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

Коэффициенты расположены в порядке возрастания, поэтому первый полином выше на самом деле равен 0.833⋅�3–5⋅�2+9.166⋅�−5. Этот набор полиномов (плюс полином Z, который я объясню позже) составляет параметры для этого конкретного экземпляра QAP. Обратите внимание, что всю работу до этого момента необходимо выполнить только один раз для каждой функции, для проверки которой вы пытаетесь использовать zk-SNARK; как только параметры QAP сгенерированы, их можно использовать повторно.

Давайте попробуем оценить все эти полиномы при =1. Вычисление полинома при =1 просто означает сложение всех коэффициентов (поскольку 1�=1 для всех �), так что это несложно. Мы получаем:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

И о чудо, то, что мы здесь имеем, точно такое же, как набор из трех векторов для первого логического элемента, который мы создали выше.

Проверка QAP

В чем же смысл этой сумасшедшей трансформации? Ответ заключается в том, что вместо проверки ограничений в R1CS по отдельности мы теперь можем проверить все ограничения одновременно выполнив проверку скалярного произведения о полиномах.

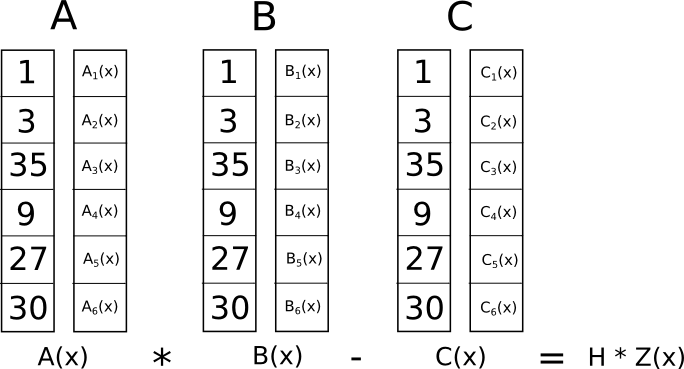
Поскольку в этом случае проверка скалярного произведения представляет собой серию сложений и умножений полиномов, результатом будет полином. Если результирующий полином, вычисляемый по каждой координате �, которую мы использовали выше для представления логического элемента, равен нулю, то это означает, что все проверки пройдены; если результирующий полином, оцененный хотя бы по одной из координат �, представляющих логический элемент, дает ненулевое значение, то это означает, что значения, входящие и выходящие из этого логического элемента, несовместимы (т. е. элемент равен ��=��⋅�� �1, но предоставленные значения могут быть �=2, ���1=2 и �=5).

Обратите внимание, что результирующий полином сам по себе не обязательно должен быть нулевым и фактически в большинстве случаев не будет; он может вести себя любое поведение в точках, которые не соответствуют каким-либо логическим элементам, пока результат равен нулю во всех точках, которые do соответствуют некоторым воротам. Чтобы проверить правильность, мы на самом деле не оцениваем полином ��=��.�⋅�.�-�.� в каждой точке, соответствующей вентилю; вместо этого мы делим � на другой многочлен � и проверяем, что � делит равномерно �, то есть деление �/� не оставляет остатка.

� определяется как (��−1)⋅(��−2)⋅(��−3)… – простейший многочлен, равный нулю во всех точках, соответствующих логическим элементам. Это элементарный факт алгебры, что любой многочлен, равный нулю во всех этих точках, должен быть кратным этому минимальному многочлену, и если многочлен кратен �, то его оценка в любой из этих точек будет равна нулю; эта эквивалентность значительно облегчает нашу работу.

Теперь давайте проверим скалярное произведение полиномов, приведенных выше. Сначала промежуточные полиномы:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

Теперь �.�⋅�.�—��.�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

Теперь минимальный многочлен ��=(��−1)⋅(��−2)⋅(��−3)⋅(��−4):

Z = [24, -50, 35, -10, 1]

И если мы разделим полученный выше результат на �, мы получим:

h = t / Z = [-3.666, 17.055, -3.444]

Без остатка.

Итак, у нас есть решение для QAP. Если мы попытаемся фальсифицировать любую из переменных в решении R1CS, из которого мы получаем это решение QAP, — скажем, установим последнюю переменную равной 31 вместо 30, то мы получим многочлен, который не проходит одну из проверок (в этом конкретном случае). В этом случае результат при =3 будет равен −1 вместо 0), и, кроме того, � не будет кратным �; скорее, деление �/� даст остаток [-5.0,8.833,-4.5,0.666].

Обратите внимание, что вышеизложенное является упрощением; «В реальном мире» сложение, умножение, вычитание и деление будут происходить не с обычными числами, а с конечными элементами поля — жуткий вид арифметики, который является самосогласованным, поэтому все алгебраические законы, которые мы знаем и любим, по-прежнему верно, но все ответы являются элементами некоторого множества конечного размера, обычно целыми числами в диапазоне от 0 до −1 для некоторого числа . Например, если �=13, то 1/2=7 (и 7⋅2=1), 3⋅5=2 и так далее. Использование арифметики с конечными полями устраняет необходимость беспокоиться об ошибках округления и позволяет системе хорошо работать с эллиптическими кривыми, которые в конечном итоге необходимы для остальной части механизма zk-SNARK, который делает протокол zk-SNARK действительно безопасным.

Особая благодарность Эрану Тромеру за то, что он помог мне объяснить многие детали внутренней работы zk-SNARK.

• SEO-контент и PR-распределение. Получите усиление сегодня.
• PlatoData.Network Вертикальный генеративный ИИ. Расширьте возможности себя. Доступ здесь.
• ПлатонАйСтрим. Интеллект Web3. Расширение знаний. Доступ здесь.
• ПлатонЭСГ. Углерод, чистые технологии, Энергия, Окружающая среда, Солнечная, Управление отходами. Доступ здесь.
• ПлатонЗдоровье. Биотехнологии и клинические исследования. Доступ здесь.
• Смещения блоков. Модернизация права собственности на экологические компенсации. Доступ здесь.
• Источник: Платон Data Intelligence.