Триплетное дерево образует одну из самых красивых структур в математике | Журнал Кванта

Большинству людей знакомо лишь несколько чисел, которые нельзя записать в виде дробей, например, $latex sqrt{2}$ или $latex pi$. Но таких чисел, называемых иррациональными числами, гораздо больше, чем дробей или рациональных чисел.

Насколько легко их аппроксимировать дробями? Если вы используете дробь со сколь угодно большим знаменателем, вы можете получить сколь угодно близкое значение. (Как известно, 22/7 дает приличное приближение к $latex pi$; 355/113 даже лучше.) Но некоторые иррациональные числа приблизить сложнее, чем другие, а это означает, что вам нужно использовать очень большой знаменатель, чтобы получить близкое приближение. Самым сложным оказывается золотое сечение, $latex phi$ или $latex (1+ sqrt{5})/2$. В специфическом математическом смысле это число, которое «дальше всего» от рационального.

Что следующее, самое дальнее? А следующий? Последовательность иррациональных чисел, которые трудно аппроксимировать, оказывается целочисленными решениями обманчиво простого уравнения, которое не имеет очевидной связи с аппроксимацией иррациональных чисел. Эту связь доказал в 1879 году выдающийся русский математик Андрей Марков.

Марков известен тем, что придумал концепцию в теории вероятностей, называемую цепями Маркова, которая используется во всем, от алгоритма Google PageRank до моделей эволюции ДНК. Но хотя решения его уравнения, называемые числами Маркова, не так хорошо известны, они возникают в широком спектре математических дисциплин, включая комбинаторику, теорию чисел, геометрию и теорию графов.

«Это не просто уравнение, это своего рода метод», — сказал Олег Карпенков, математик из Ливерпульского университета. «Эти числа занимают центральное место, глубоко внутри математики… структуры, подобные этой, представляют собой редкие идеи».

Его уравнение $latex x^2+y^2+z^2=3xyz$ имеет очевидное целочисленное решение, когда x, y и z все равны 1 (поскольку 1 + 1 + 1 = 3 × 1). Оказывается, все целочисленные решения уравнения связаны простым правилом. Начни с решения(a, b, c). Тогда соответствующая тройка (a, b, 3 ab - c) тоже решение. Первые два числа остаются прежними, а c, третий, заменяется на 3аб - с. Примените это правило к (1, 1, 1), и вы получите (1, 1, 2). (Легко проверить, что при вводе этих значений обе части уравнения равны 6.) Примените правило еще раз, и вы вернетесь к тому, с чего начали, поскольку 3 − 2 = 1. Но если вы перевернете порядок чисел числа в тройке, прежде чем применять правило, создается целая вселенная решений. Введите (1, 2, 1) и вы получите (1, 2, 5).

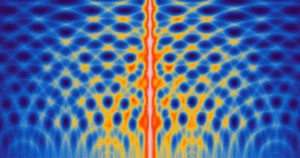
До сих пор из-за одинаковых единиц дерево (показанное на иллюстрации в начале этой истории) не ветвится — с первых шагов вырастает, так сказать, ствол дерева. Но если вы начнете с решения с тремя разными числами, например (1, 1, 2), ветви начнут размножаться. Введите (5, 5, 1) и вы получите (2, 2, 5). Но (29, 2, 5) приводит к (1, 1, 5). (Если вы введете (13), то правило вернет вас обратно на более низкую ветвь дерева.) С этого момента каждое решение имеет три разных числа, поэтому каждая ветвь дерева ведет к двум новым ветвям. .

Крайняя левая ветвь дерева может показаться знакомой — она содержит все остальные числа последовательности Фибоначчи, одной из самых известных в математике (каждое число в этой последовательности представляет собой сумму двух предыдущих членов: 1, 1, 2, 3, 5, 8, 13, 21, 34, …). Крайняя правая ветвь аналогичным образом содержит все остальные термины последовательности Пелла, родственной, хотя и немного менее известной, последовательности. То, как эти последовательности появляются на дереве решений, — «одна из самых прекрасных вещей в математике, которую я знаю», — сказал Александр Гамбурд, профессор Городского университета Нью-Йорка.

Теорема Маркова 1879 года, связывающая каждую тройку с трудно аппроксимируемым иррациональным числом, была первым намеком на то, что это уравнение может найти глубокий отклик во всей математике. В Книга 2013 года на эту темуМартин Айгнер, австрийский математик, умерший в октябре, назвал эту теорему «без сомнения, одной из классических произведений всех времен в теории чисел».

В 1913 году Георг Фробениус, немецкий математик, сделавший широкий вклад алгебре, теории чисел и изучению дифференциальных уравнений, заметил кое-что любопытное в марковских тройках. Каждое наибольшее число, казалось, однозначно определяло два меньших. Число — например, 5 — может встречаться во многих тройках, например (1, 2, 5), (1, 5, 13), (2, 5, 29) и так далее. Но, заметил он, если вы посмотрите только на самое большое число в каждой тройке, оно будет связано только с одной парой меньших чисел.

Поскольку цифры растут так быстро, далеко не очевидно, что это так. Например, возьмем тройку (5, 433, 6,466). Неочевидно, что если вы установите z до 6,466, единственно возможного x и y которые решат уравнение, — это 5 и 433. Но, насколько мог судить Фробениус, наибольшее число всегда однозначно определяло два меньших. За прошедшие с тех пор 110 лет, несмотря на огромное количество исследований, связывающих числа Маркова с другими проблемами, никто не смог доказать то, что стало известно как гипотеза единственности.

Относительная простота гипотезы иллюстрирует общий математический парадокс. Такие инструменты, как уравнение Маркова, можно использовать для доказательства тонких и сложных результатов, даже если основные вопросы об их свойствах остаются нерешенными.

Однако за последние несколько лет произошел заметный прогресс в доказательстве гипотезы единственности. Давно известно, что между каждой марковской тройкой и всеми дробями между нулем и 1 можно создать соответствие. Для каждой дроби p/q, который называется индексом, можно присвоить число Маркова m_p/q следуя определенной математической процедуре. Например, m_2/3 29, и m_3/5 это 433.

В 2013 году Айгнер выдвинул три гипотезы о том, как можно упорядочить тройки с помощью этого соответствия. Эти гипотезы являются ступеньками на пути к доказательству гипотезы единственности. Он предположил, что если оставить числитель индекса постоянным и увеличить знаменатель (как в 1/2, 1/3, 1/4, 1/5, …), соответствующие числа Маркова будут продолжать увеличиваться. Точно так же он думал, что если вы увеличите числитель, но сохраните тот же знаменатель (как в 1/17, 2/17, 3/17, 4/17, …), вы также должны получить строку все больших чисел Маркова. По его мнению, та же самая закономерность увеличения чисел должна сохраняться, если сумма числителя и знаменателя остается постоянной (как в 1/100, 2/99, 3/98,…).

Гипотеза о постоянном числителе была доказана в бумага 2020 in Достижения в математике by Мишель Рабидо Университета Хартфорда и Ральф Шиффлер Университета Коннектикута. В феврале 2023 года вместе с двумя другими сотрудниками Рабидо и Шиффлер опубликовали доказательство еще две гипотезы так же.

Благодаря этим и другим достижениям Карпенков с оптимизмом смотрит на то, что доказательство гипотезы Фробениуса о единственности, наконец, может быть в разработке. «Я знаю людей, которые говорят, что близки к тому, чтобы доказать это», — сказал он. «Я думаю, что мы довольно близки — возможно, в течение следующих пяти лет».

Quanta проводит серию опросов, чтобы лучше обслуживать нашу аудиторию. Возьми наш опрос читателей по математике и вы будете участвовать в бесплатном выигрыше Quanta мерч.