Ортонормальные основы экстремальной квантовости

Переиздано Платоном

Читают: 0

Марцин Рудзиньски^1,2, Адам Бурхардт³и Кароль Жичковски^1,4

¹Факультет физики, астрономии и прикладной информатики Ягеллонского университета, ул. Łojasiewicza 11, 30-348 Краков, Польша
²Докторантура точных и естественных наук, Ягеллонский университет, ул. Лоясевича 11, 30-348 Краков, Польша
³QuSoft, CWI и Амстердамский университет, Научный парк 123, 1098 XG Амстердам, Нидерланды
⁴Центр теоретической физики, Польская академия наук, Ал. Lotników 32/46, 02-668 Варшава, Польша

Находите эту статью интересной или хотите обсудить? Scite или оставить комментарий на SciRate.

Абстрактные

Спиновые антикогерентные состояния в последнее время привлекли к себе большое внимание как наиболее «квантовые» состояния. Некоторые когерентные и антикогерентные спиновые состояния известны как оптимальные квантовые ротосенсоры. В данной работе мы вводим меру квантовости ортонормированных базисов спиновых состояний, определяемую средней антикогерентностью отдельных векторов и энтропией Верля. Таким образом, мы идентифицируем наиболее когерентные и наиболее квантовые состояния, которые приводят к ортогональным измерениям предельной квантовости. Их симметрию можно выявить с помощью звездного представления Майораны, которое обеспечивает интуитивное геометрическое представление чистого состояния точками на сфере. Полученные результаты приводят к максимально (минимально) запутанным базисам в $2j+1$-мерном симметричном подпространстве $2^{2j}$-мерного пространства состояний многочастных систем, составленных из $2j$ кубитов. Некоторые найденные основания являются изокогерентными, поскольку состоят из всех состояний одинаковой степени спиновой когерентности.

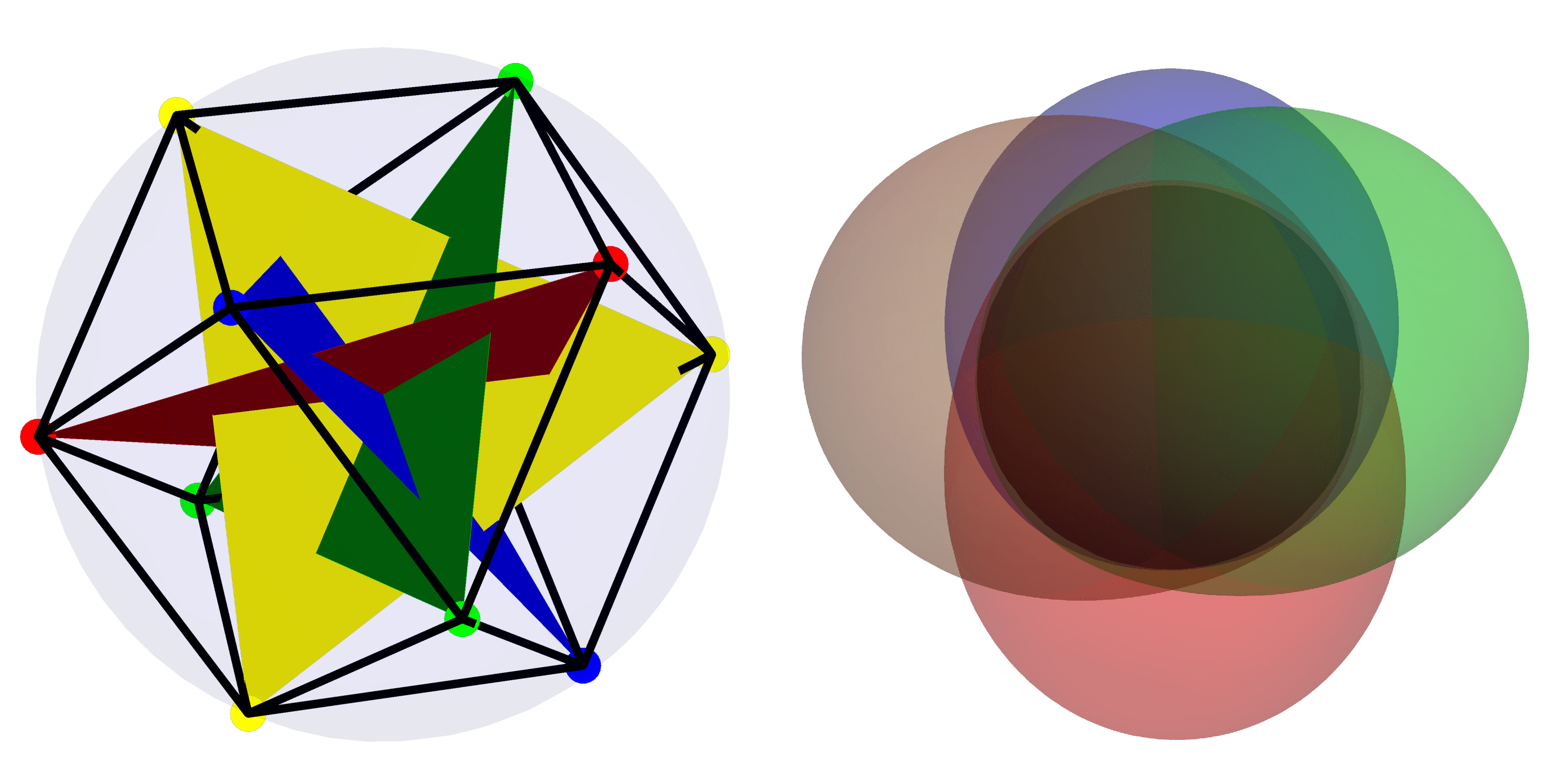
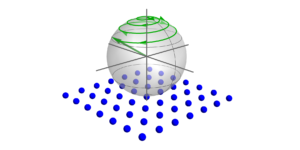
Рекомендованное изображение: На левом изображении самый «квантовый» базис в $mathcal{H}_4$ изображен в звездном представлении. Справа представлена функция Хусими для состояний в наиболее когерентном («классическом») базисе в рамках $mathcal{H}_4$.

► Данные BibTeX

@article{Rudzinski2024orthonormalbasesof, дои = {10.22331/q-2024-01-25-1234}, URL = {https://doi.org/10.22331/q-2024-01-25-1234}, title = {Ортонормированные базисы крайней квантовости}, автор = {Рудзи{'{n}}ски, Марцин и Бурхардт, Адам и {.{Z}}ычковский, Кароль}, журнал = {{Квант}}, иссн = {2521-327X}, издатель = {{Verein zur F{"{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, объем = {8}, страницы = {1234}, месяц = январь, год = {2024} }

► Рекомендации

[1] Т. Франкель, Геометрия физики: введение, 3-е изд., Cambridge University Press (2011).
https: / / doi.org/ 10.1017 / CBO9781139061377

[2] Д. Хрущиньский и А. Ямиолковский, Геометрические фазы в классической и квантовой механике, Биркхойзер (2004).
https://doi.org/10.1007/978-0-8176-8176-0

[3] Д.А. Ли, Геометрическая относительность, Американское математическое общество, Провиденс (2021).
https: / / doi.org/ 10.1090 / GSM / 201

[4] И. Бенгтссон и К. Жичковски, Геометрия квантовых состояний: введение в квантовую запутанность, 2-е изд., Cambridge University Press (2017).
https: / / doi.org/ 10.1017 / 9781139207010

[5] М. Левин, Геометрические методы для нелинейных квантовых систем многих тел, J. Functional Analysis 260, 12, (2011).
https: / / doi.org/ 10.1016 / j.jfa.2010.11.017

[6] Э. Коэн, Х. Ларок, Ф. Бушар и др., Геометрическая фаза от Ааронова – Бома до Панчаратнама – Берри и далее, Nat. Преподобный физ. 1, 437–449 (2019).
https://doi.org/10.1038/s42254-019-0071-1

[7] E. Majorana Atomi orientati в переменной кампо магнито, Nuovo Cimento 9, 43–50 (1932).
https: / / doi.org/ 10.1007 / BF02960953

[8] Р. Барнетт, А. Тернер и Э. Демлер, Классификация новых фаз спинорных атомов, Phys. Преподобный Летт. 97, 180412 (2006).
https: / / doi.org/ 10.1103 / PhysRevLett.97.180412

[9] Р. Барнетт, А. Тернер и Э. Демлер, Классификация вихрей в $S=3$ конденсатах Бозе-Эйнштейна, Phys. Ред. А 76, 013605 (2007).
https: / / doi.org/ 10.1103 / PhysRevA.76.013605

[10] Х. Мякеля и К.-А. Суоминен, Инертные состояния спин-s-систем, Физ. Преподобный Летт. 99, 190408 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.190408

[11] Э. Серрано-Энсастига и Ф. Мирелес, Фазовая характеристика спинорных конденсатов Бозе-Эйнштейна: подход майорановского звездного представления, Phys. Летт. А 492, 129188 (2023).
https: / / doi.org/ 10.1016 / j.physleta.2023.129188

[12] П. Матонет и др., Эквивалентность запутанности симметричных состояний $N$-кубита, Phys. Ред. А 81, 052315 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.052315

[13] Ж. Мартин, О. Жиро, П. А. Браун, Д. Браун и Т. Бастин, Многокубитные симметричные состояния с высокой геометрической запутанностью, Phys. Ред. А 81, 062347 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.062347

[14] М. Аулбах, DJH Маркхэм и М. Мурао, Максимально запутанное симметричное состояние с точки зрения геометрической меры, New J. Phys. 12, 073025 (2010).
https://doi.org/10.1088/1367-2630/12/7/073025

[15] DJH Markham, Запутанность и симметрия в перестановочно-симметричных состояниях, Phys. Ред. А 83, 042332 (2011).
https: / / doi.org/ 10.1103 / PhysRevA.83.042332

[16] П. Рибейро, Р. Моссери, Запутывание в симметричном секторе $n$ кубитов, Phys. Преподобный Летт. 106, 180502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.106.180502

[17] М.Аульбах, Классификация запутанности в симметричных состояниях, Межд. Ж. Квантум Информ. 10, 1230004 (2012).
https: / / doi.org/ 10.1142 / S0219749912300045

[18] В. Ганчарек, М. Кусь и К. Жичковски, Барицентрическая мера квантовой запутанности, Phys. Ред. А 85, 032314 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.032314

[19] А. Мандилара, Т. Кудро, А. Келлер и П. Милман, Классификация чистых симметричных состояний по запутанности через спин-когерентные состояния, Phys. Ред. А 90, 050302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.050302

[20] П. Хиллус и др., Информация Фишера и многочастичная запутанность, Phys. Ред. А 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[21] Дж. Хэнней, Фаза Берри для спина в представлении Майораны, J. Phys. А: Математика. Быт. 31, L53 (1998).
https://doi.org/10.1088/0305-4470/31/2/002

[22] П. Бруно, Квантово-геометрическая фаза в звездном представлении Майораны: отображение на многочастичной фазе Ааронова-Бома, Phys. Преподобный Летт. 108, 240402 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.240402

[23] HD Лю и Л.Б. Фу, Фаза Берри и квантовая запутанность в звездном представлении Майораны, Phys. Ред. А 94, 022123 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.022123

[24] П. Рибейро, Дж. Видал и Р. Моссери, Термодинамический предел модели Липкина-Мешкова-Глика, Phys. Преподобный Летт. 99, 050402 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.050402

[25] П. Рибейро, Дж. Видал и Р. Моссери, Точный спектр модели Липкина-Мешкова-Глика в термодинамическом пределе и поправках конечного размера, Phys. Ред. Е 78, 021106 (2008).
https: / / doi.org/ 10.1103 / PhysRevE.78.021106

[26] Дж. Зимба, «Антикогерентные» спиновые состояния через представление Майораны, Электрон. Дж. Теория. Физ. 3, 143 (2006).
https:///api.semanticscholar.org/CorpusID:13938120

[27] Д. Багет, Т. Бастин, Дж. Мартин, Мультикбитные симметричные состояния с максимально смешанными однобитными редукциями, Phys. Rev. A 90, 032314 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.032314

[28] О. Жиро, Д. Браун, Д. Багет, Т. Бастин и Дж. Мартин, Тензорное представление спиновых состояний, Phys. Преподобный Летт. 114, 080401 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.080401

[29] D. Baguette, F. Damanet, O. Giraud, J. Martin. Антигогерентность спиновых состояний с симметриями точечной группы, Phys. Rev. A 92, 052333 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.92.052333

[30] Х.Д. Лю, Л.Б. Фу, X. Ван, Когерентный подход к представлению Майораны, Commun. Теор. Физ. 67, 611 (2017).
https://doi.org/10.1088/0253-6102/67/6/611

[31] Д. Багет и Дж. Мартин, Меры антикогерентности для чистых спиновых состояний, Phys. Ред. А 96, 032304 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.032304

[32] П. Колендерски и Р. Демкович-Добжанский, Оптимальное состояние для поддержания выровненных систем отсчета и платоновых тел, Phys. Ред. А 78, 052333 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052333

[33] К. Криссомалакос и Х. Эрнандес-Коронадо, Оптимальные квантовые ротосенсоры, Phys. Ред. А 95, 052125 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.95.052125

[34] AZ Goldberg и DFV James, Квантово-ограниченные измерения угла Эйлера с использованием антикогерентных состояний, Phys. Ред. А 98, 032113 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032113

[35] Ж. Мартин, С. Вейгерт и О. Жиро, Оптимальное обнаружение вращений вокруг неизвестных осей с помощью когерентных и антикогерентных состояний, Quantum 4, 285 (2020).
https://doi.org/10.22331/q-2020-06-22-285

[36] Дж. Крэнн, Д. В. Крибс и Р. Перейра, Сферические конструкции и антикогерентные спиновые состояния, J. Phys. А: Математика. Теор. 43, 255307 (2010).
https://doi.org/10.1088/1751-8113/43/25/255307

[37] Э. Баннаи и М. Тагами, Заметка об антикогерентных спиновых состояниях, J. Phys. А: Математика. Теор. 44, 342002 (2011).
https://doi.org/10.1088/1751-8113/44/34/342002

[38] М. Ван и Ю. Чжу, Антикогерентные состояния со спином 2 и сферические конструкции, J. Phys. А: Математика. Теор. 55, 425304 (2022).
https://doi.org/10.1088/1751-8121/ac971d

[39] А.З. Гольдберг, А.Б. Климов, М.Грассл, Г. Лейхс и Л.Л. Санчес-Сото, Экстремальные квантовые состояния, AVS Quantum Sci. 2, 044701 (2020).
https: / / doi.org/ 10.1116 / 5.0025819

[40] AZ Goldberg, M. Grassl, G. Leuchs и LL Sanchez-Soto, Quantumness за пределами запутанности: случай симметричных состояний, Phys. Ред. А 105, 022433 (2022).
https: / / doi.org/ 10.1103 / PhysRevA.105.022433

[41] О. Жиро, П. Браун и Д. Браун, Количественная оценка квантовости и поиск королев квантов, New J. Phys. 12, 063005 (2010).
https://doi.org/10.1088/1367-2630/12/6/063005

[42] Р. Дельбурго, Состояния минимальной неопределенности для группы вращения и родственных групп, J. Phys. А 10, Л233 (1977).
https://doi.org/10.1088/0305-4470/10/11/012

[43] А. Верль, О связи между классической и квантово-механической энтропией, Rep. Math. Физ. 16, 353 (1979).
https://doi.org/10.1016/0034-4877(79)90070-3

[44] Э. Х. Либ, Доказательство энтропийной гипотезы Верля, Коммун. Математика. Физ. 62, 35 (1978).
https: / / doi.org/ 10.1007 / BF01940328

[45] CT Lee, Энтропия спиновых состояний Верля и гипотеза Либа, J. Phys. А 21, 3749 (1988).
https://doi.org/10.1088/0305-4470/21/19/013

[46] Э. Х. Либ и Дж. П. Соловей, Доказательство энтропийной гипотезы для когерентных спиновых состояний Блоха и ее обобщений, Acta Math. 212, 379 (2014).
https://doi.org/10.1007/s11511-014-0113-6

[47] Ф. Бушар и др., Квантовая метрология на пределе с экстремальными майорановскими созвездиями, Optica 4, 1429–1432 (2017).
https: / / doi.org/ 10.1364 / OPTICA.4.001429

[48] А. Верль, Общие свойства энтропии, Rev. Mod. Физ. 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[49] А. Верль, Многогранность энтропии, Rep. Math. Физ. 30, 119 (1991).
https://doi.org/10.1016/0034-4877(91)90045-O

[50] С. Гнутцманн и К. Жичковский, Энтропия Реньи-Верля как мера локализации в фазовом пространстве, J. Phys. А 34, 10123 (2001).
https://doi.org/10.1088/0305-4470/34/47/317

[51] К. Жичковский, Локализация собственных состояний и средняя энтропия Верля, Physica E 9, 583 (2001).
https://doi.org/10.1016/S1386-9477(00)00266-6

[52] Л. Л. Санчес-Сото, А. Б. Климов, П. де ла Оз и Г. Лейхс, Квантовые и классические состояния поляризации: когда учитываются мультиполи, J. Phys. Б 46 104011 (2013).
https://doi.org/10.1088/0953-4075/46/10/104011

[53] А. Таваколи и Н. Гизин, Платоновые тела и фундаментальные тесты квантовой механики, Quantum 4, 293 (2020).
https://doi.org/10.22331/q-2020-07-09-293

[54] Х.Ч. Нгуен, С. Дизайноль, М. Баракат и О. Гюне, Симметрии между измерениями в квантовой механике, препринт arXiv:2003.12553 (2022).
https:///doi.org/10.48550/arXiv.2003.12553
Arxiv: 2003.12553

[55] Дж. И. Латорре, Г. Сьерра, Платоническая запутанность, Quantum Inf. Вычислить. 21, 1081 (2021).
https: / / doi.org/ 10.26421 / QIC21.13-14-1

[56] К. Болонек-Ласонь, П. Косинский, Группы, Платоновы тела и неравенства Белла, Quantum 5, 593 (2021).
https://doi.org/10.22331/q-2021-11-29-593

[57] К. Ф. Пал, Т. Вертези, Группы, платоновые неравенства Белла для всех измерений, Quantum 6, 756 (2022).
https://doi.org/10.22331/q-2022-07-07-756

[58] Р. Х. Дике, Когерентность в процессах спонтанного излучения, Phys. Откр. 93, 99 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99

[59] В. Каримипур, Л. Мемарзаде, Равнозапутанные базисы в произвольных измерениях Phys. Ред. А 73, 012329 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.73.012329

[60] Г. Райхель, А. Гонсиоровски и К. Жичковский, Робастные матрицы Адамара, унистохастические лучи в многограннике Биркгофа и равнозапутанные основания в составных пространствах. Матем. Комп. наук. 12, 473 (2018).
https: / / doi.org/ 10.1007 / s11786-018-0384-й

[61] Дж. Чартовский, Д. Гойенече, М. Грассл и К. Жичковски, Изоперепутанные взаимно несмещенные основания, симметричные квантовые измерения и конструкции со смешанными состояниями, Phys. Преподобный Летт. 124, 090503 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.124.090503

[62] Ф. Дель Санто, Дж. Чартовский, К. Жичковский и Н. Гизин, Изо-запутанные основания и измерения суставов, препринт arXiv: 2307.06998 (2023).
https:///doi.org/10.48550/arXiv.2307.06998
Arxiv: 2307.06998

[63] Р. Пенроуз, «О нелокальности Белла без вероятностей: немного любопытной геометрии», «Квантовые отражения» (2000).

[64] Дж. Зимба и Р. Пенроуз, О нелокальности Белла без вероятностей: более любопытная геометрия, Stud. Хист. Фил. наук. 24, 697 (1993).
https://doi.org/10.1016/0039-3681(93)90061-N

[65] Дж. Э. Массад и П. К. Аравинд, Новый взгляд на додекаэдр Пенроуза, Am. J. Physics 67, 631 (1999).
https: / / doi.org/ 10.1119 / 1.19336

[66] Хусими К. «Некоторые формальные свойства матрицы плотности» // Тр. Физ. Математика. Соц. 22, 264 (1940).
https: / / doi.org/ 10.11429 / ppmsj1919.22.4_264

[67] В. Сломчинский и К. Жичковский, Средняя динамическая энтропия квантовых отображений на сфере расходится в квазиклассическом пределе, Phys. Преподобный Летт. 80, 1880 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.1880

[68] М. Пиотрак, М. Копчух, А.Д. Фард, М. Смолис, С. Пустельный, К. Корзеква, Совершенные квантовые транспортиры, препринт arXiv:2310.13045 (2023).
https:///doi.org/10.48550/arXiv.2310.13045
Arxiv: 2310.13045

[69] NCN Maestro 7 2015/18/A/ST2/00274 веб-сайт https://chaos.if.uj.edu.pl/ karol/Maestro7/files/data3/Numerical_Results.dat.
https://chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

[70] Д. Вайнгартен, Асимптотическое поведение групповых интегралов в пределе бесконечного ранга, J. Math. Физ. 19, 999 (1978).
https: / / doi.org/ 10.1063 / 1.523807

[71] Коллинз Б., Сниади П. Интегрирование по мере Хаара на унитарной, ортогональной и симплектической группе, Сообщ. Математика. Физ. 264, 773 (2006).
https://doi.org/10.1007/s00220-006-1554-3

[72] Г. Райчел, Квантовые отображения и конструкции, Кандидатская диссертация, препринт arXiv:2204.13008 (2022).
https:///doi.org/10.48550/arXiv.2204.13008
Arxiv: 2204.13008

[73] Д. Мартин и Е. П. Вигнер, Теория групп и ее применение к квантовой механике атомных спектров, Academic Press Inc., Нью-Йорк (1959).
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

Цитируется

[1] Михал Пиотрак, Марек Копчух, Араш Дежан Фард, Магдалена Смолис, Шимон Пустельный и Камиль Корзеква, «Совершенные квантовые транспортиры», Arxiv: 2310.13045, (2023).

[2] Аарон З. Голдберг, «Корреляции для подмножеств частиц в симметричных состояниях: что фотоны делают в луче света, когда остальные игнорируются», Arxiv: 2401.05484, (2024).

Приведенные цитаты из САО / НАСА ADS (последнее обновление успешно 2024-01-25 11:53:23). Список может быть неполным, поскольку не все издатели предоставляют подходящие и полные данные о цитировании.

Не удалось получить Перекрестная ссылка на данные во время последней попытки 2024-01-25 11:53:22: Не удалось получить цитируемые данные для 10.22331 / q-2024-01-25-1234 от Crossref. Это нормально, если DOI был зарегистрирован недавно.

Эта статья опубликована в Quantum под Creative Commons Attribution 4.0 International (CC BY 4.0) лицензия. Авторское право остается за первоначальными правообладателями, такими как авторы или их учреждения.

SEO-контент и PR-распределение. Получите усиление сегодня.
PlatoData.Network Вертикальный генеративный ИИ. Расширьте возможности себя. Доступ здесь.
ПлатонАйСтрим. Интеллект Web3. Расширение знаний. Доступ здесь.
ПлатонЭСГ. Углерод, чистые технологии, Энергия, Окружающая среда, Солнечная, Управление отходами. Доступ здесь.
ПлатонЗдоровье. Биотехнологии и клинические исследования. Доступ здесь.
Источник: https://quantum-journal.org/papers/q-2024-01-25-1234/

Отметка времени: 25 января 2024

Отметка времени: 3 октября, 2023

Ортонормированные базисы крайней квантовости

Переиздано Платоном

Абстрактные

Популярное резюме

► Данные BibTeX

► Рекомендации

Цитируется

Больше от Квантовый журнал

Улучшенные протоколы DIQKD с анализом конечного размера

Дистанционно управляемая генерация запутанности

Быстрое квантовое разделение цепей с рандомизированными измерениями

Генерация на основе измерений и сохранение состояний кота и сетки в кластерном состоянии с непрерывной переменной

Подготовка состояния в модели Гейзенберга через адиабатическое спиральное движение

MQT Bench: программное обеспечение для сравнительного анализа и инструменты автоматизации проектирования для квантовых вычислений

Ограничения аналитичности ограничивают распад спектрального формфактора

Вариационные решения отображений фермионов в кубиты в двух пространственных измерениях

Доказуемо точное моделирование калибровочных теорий и бозонных систем

Квантовое кодирование и анализ непрерывных стохастических процессов с использованием финансовых приложений

О Нас

Вертикальный поиск и AI

Платформа

Оставайтесь на связи

Учетная запись