Bases ortonormais de extrema quantumidade

Bases ortonormais de extrema quantumidade

Carimbo de data / hora: 25 de janeiro de 2024 6h51
Nó Fonte: 3083690

Marcin Rudzinski1,2, Adam Burchardt3 e Karol Życzkowski1,4

1Faculdade de Física, Astronomia e Ciência da Computação Aplicada, Universidade Jagiellonian, ul. Łojasiewicza 11, 30-348 Cracóvia, Polônia
2Escola de Doutorado em Ciências Exatas e Naturais, Universidade Jaguelônica, ul. Łojasiewicza 11, 30-348 Cracóvia, Polônia
3QuSoft, CWI e Universidade de Amsterdã, Science Park 123, 1098 XG Amsterdã, Holanda
4Centro de Física Teórica, Academia Polonesa de Ciências, Al. Lotników 32/46, 02-668 Warszawa, Polônia

Acha este artigo interessante ou deseja discutir? Scite ou deixe um comentário no SciRate.

Sumário

Os estados anticoerentes de spin adquiriram recentemente muita atenção como os estados mais “quânticos”. Alguns estados de spin coerentes e anticoerentes são conhecidos como rotossensores quânticos ideais. Neste trabalho, introduzimos uma medida de quantum para bases ortonormais de estados de spin, determinada pela anticoerência média de vetores individuais e pela entropia de Wehrl. Desta forma, identificamos os estados mais coerentes e quânticos, que levam a medições ortogonais de extrema quântica. Suas simetrias podem ser reveladas usando a representação estelar de Majorana, que fornece uma representação geométrica intuitiva de um estado puro por pontos em uma esfera. Os resultados obtidos levam a bases maximamente (minimamente) emaranhadas no subespaço simétrico dimensional $2j+1$ do espaço dimensional $2^{2j}$ de estados de sistemas multipartidos compostos por $2j$ qubits. Algumas bases encontradas são isocoerentes, pois consistem em todos os estados com o mesmo grau de coerência de spin.

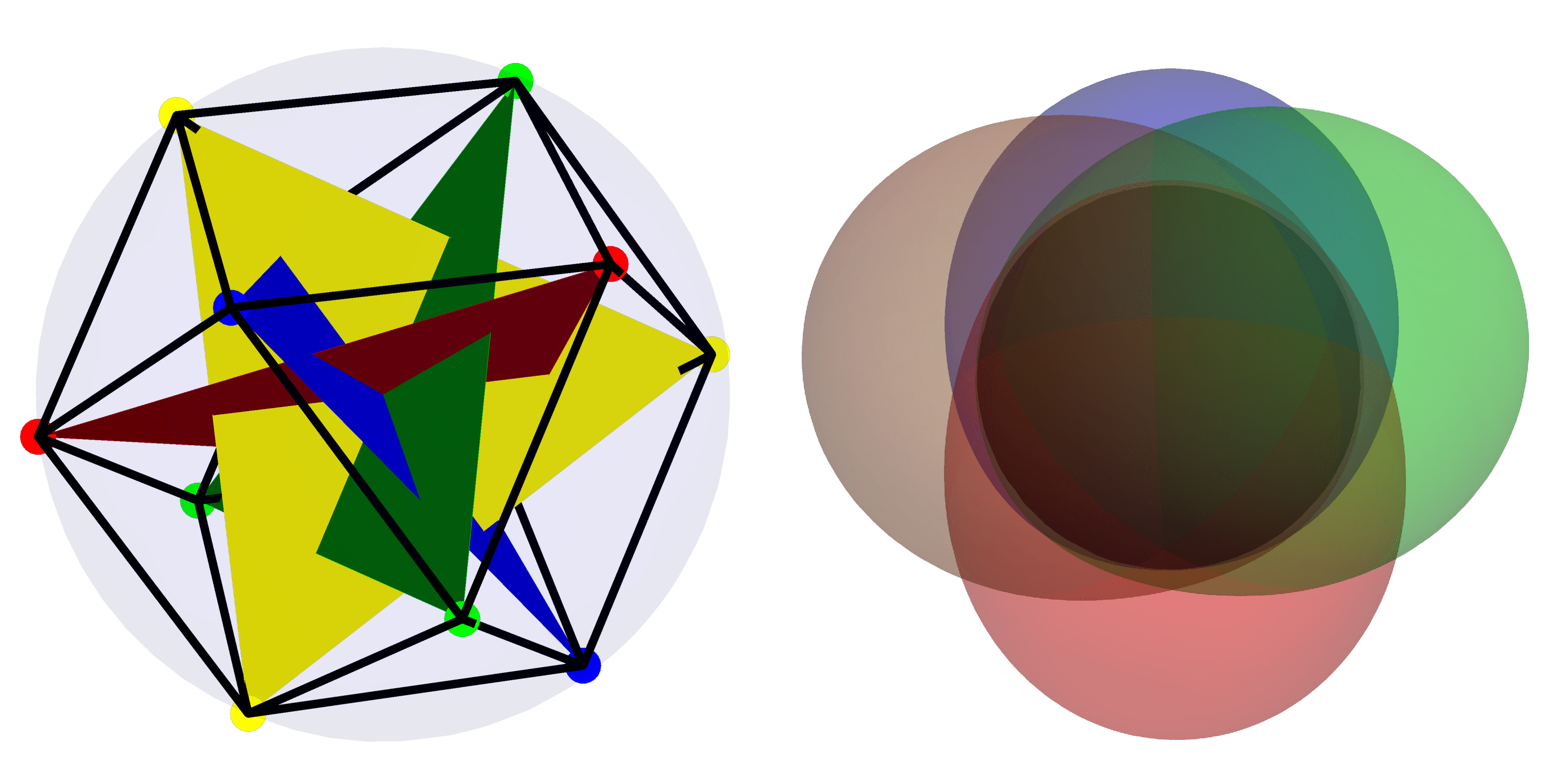
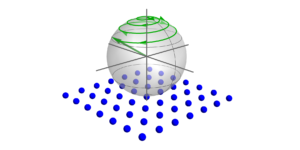
Imagem em destaque: Na imagem à esquerda, a base mais “quântica” em $mathcal{H}_4$ é representada usando a representação estelar. À direita, é apresentada a função Husimi para estados na base mais coerente (“clássica”) dentro de $mathcal{H}_4$.

Resumo popular

Extremal states, coherent and anticoherent, have practical applications in quantum metrology as optimal rotosensors. This work provides a natural extension of previous studies concerning the search for such states proposing optimal orthogonal measurements of Lüders and von Neumann of the extreme spin coherence. We introduce the measure $mathcal{B}_t$ as the tool to characterize the quantumness of a measurement given by a basis in $mathcal{H}_N$. The search for the most quantum bases for $N=3,4,5$ and $7$ is performed. Numerical results suggest, that the obtained solutions are unique. A set of candidates for the “classical” bases consisting of the most spin-coherent states is indicated for $N=3,4,5,6$. Some of the most quantum bases, analyzed in the stellar representation of Majorana, reveal symmetries of Platonic solids. Most classical bases display symmetric structures too. We also considered other measures of the quantumness of vectors forming a given basis. Optimization of the mean Wehrl entropy of $N$ orthogonal vectors leads to the same bases distinguished by extremal values of the quantities $mathcal{B}_t$, with a single exception of the quantum basis for $N=6$.

► dados BibTeX

► Referências

[1] T. Frankel, A Geometria da Física: Uma Introdução, 3ª ed., Cambridge University Press (2011).
https: / / doi.org/ 10.1017 / CBO9781139061377

[2] D. Chruściński e A. Jamiołkowski, Fases Geométricas em Mecânica Clássica e Quântica, Birkhäuser (2004).
https:/​/​doi.org/​10.1007/​978-0-8176-8176-0

[3] DA Lee, Relatividade geométrica, American Mathematical Society, Providence (2021).
https: / / doi.org/ 10.1090 / gsm / 201

[4] I. Bengtsson e K. Życzkowski, Geometria dos Estados Quânticos: Uma Introdução ao Emaranhamento Quântico, 2ª ed., Cambridge University Press (2017).
https: / / doi.org/ 10.1017 / 9781139207010

[5] M. Lewin, Métodos geométricos para sistemas quânticos não lineares de muitos corpos, J. Functional Analysis 260, 12, (2011).
https: / / doi.org/ 10.1016 / j.jfa.2010.11.017

[6] E. Cohen, H. Larocque, F. Bouchard et al., Fase geométrica de Aharonov – Bohm a Pancharatnam – Berry e além, Nat. Rev. 1, 437–449 (2019).
https:/​/​doi.org/​10.1038/​s42254-019-0071-1

[7] E. Majorana Atomi orientati em campo magnético variável, Nuovo Cimento 9, 43-50 (1932).
https: / / doi.org/ 10.1007 / BF02960953

[8] R. Barnett, A. Turner e E. Demler, Classificando novas fases de átomos espinor, Phys. Rev. 97, 180412 (2006).
https: / / doi.org/ 10.1103 / PhysRevLett.97.180412

[9] R. Barnett, A. Turner e E. Demler, Classificando vórtices em $S=3$ Condensados ​​de Bose-Einstein, Phys. Rev.A 76, 013605 (2007).
https: / / doi.org/ 10.1103 / PhysRevA.76.013605

[10] H. Mäkelä e K.-A. Suominen, Estados inertes de sistemas de spin-s, Phys. Rev. 99, 190408 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.190408

[11] E. Serrano-Ensástiga e F. Mireles, Caracterização de fase de condensados ​​espinor de Bose-Einstein: uma abordagem de representação estelar de Majorana, Phys. Vamos. A 492, 129188 (2023).
https: / / doi.org/ 10.1016 / j.physleta.2023.129188

[12] P. Mathonet et al., Equivalência de emaranhamento de estados simétricos de $N$-qubit, Phys. Rev. A 81, 052315 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.052315

[13] J. Martin, O. Giraud, PA Braun, D. Braun e T. Bastin, Estados simétricos multiqubit com alto emaranhamento geométrico, Phys. Rev.A 81, 062347 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.062347

[14] M. Aulbach, DJH Markham e M. Murao, O estado simétrico maximamente emaranhado em termos de medida geométrica, New J. Phys. 12, 073025 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​7/​073025

[15] DJH Markham, Emaranhamento e simetria em estados simétricos de permutação, Phys. Rev.A 83, 042332 (2011).
https: / / doi.org/ 10.1103 / PhysRevA.83.042332

[16] P. Ribeiro e R. Mosseri, Emaranhamento no setor simétrico de $n$ qubits, Phys. Rev. 106, 180502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.106.180502

[17] M.Aulbach, Classificação de emaranhamento em estados simétricos, Int. J. Informação Quântica. 10, 1230004 (2012).
https: / / doi.org/ 10.1142 / S0219749912300045

[18] W. Ganczarek, M. Kuś e K. Życzkowski, medida baricêntrica de emaranhamento quântico, Phys. Rev.A 85, 032314 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.032314

[19] A. Mandilara, T. Coudreau, A. Keller e P. Milman, Classificação de emaranhamento de estados simétricos puros via estados coerentes de spin, Phys. Rev. A 90, 050302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.050302

[20] P. Hyllus, at al., Informação de Fisher e emaranhamento de partículas múltiplas, Phys. Rev.A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[21] JH Hannay, A fase Berry para rotação na representação Majorana, J. Phys. R: Matemática. Gênesis 31, L53 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​2/​002

[22] P. Bruno, Fase Geométrica Quântica na Representação Estelar de Majorana: Mapeando em uma Fase Aharonov-Bohm de muitos corpos, Phys. Rev. 108, 240402 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.240402

[23] HD Liu e LB Fu, fase Berry e emaranhamento quântico na representação estelar de Majorana, Phys. Rev. A 94, 022123 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.022123

[24] P. Ribeiro, J. Vidal e R. Mosseri, Limite termodinâmico do modelo Lipkin-Meshkov-Glick, Phys. Rev. 99, 050402 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.050402

[25] P. Ribeiro, J. Vidal e R. Mosseri, Espectro exato do modelo Lipkin-Meshkov-Glick no limite termodinâmico e correções de tamanho finito, Phys. Rev. E 78, 021106 (2008).
https: / / doi.org/ 10.1103 / PhysRevE.78.021106

[26] J. Zimba, Estados de spin “Anticoerentes” através da Representação de Majorana, Elétron. J. Teor. Física. 3, 143 (2006).
https://​/​api.semanticscholar.org/​CorpusID:13938120

[27] D. Baguette, T. Bastin e J. Martin, Estados simétricos multiqubit com reduções de um qubit maximamente mistas, Phys. Rev. A 90, 032314 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.032314

[28] O. Giraud, D. Braun, D. Baguette, T. Bastin e J. Martin, Representação tensorial de estados de spin, Phys. Rev. Lett. 114, 080401 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.080401

[29] D. Baguette, F. Damanet, O. Giraud e J. Martin, Anticoerência de estados de spin com simetrias de grupos pontuais, Phys. Rev. A 92, 052333 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.92.052333

[30] HD Liu, LB Fu, X. Wang, Abordagem de estado coerente para representação de Majorana, Commun. Teoria. Física. 67, 611 (2017).
https:/​/​doi.org/​10.1088/​0253-6102/​67/​6/​611

[31] D. Baguette e J. Martin, Medidas de anticoerência para estados de spin puros, Phys. Rev. A 96, 032304 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.032304

[32] P. Kolenderski e R. Demkowicz-Dobrzański, Estado ideal para manter os referenciais alinhados e os sólidos platônicos, Phys. Rev.A 78, 052333 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052333

[33] C. Chryssomalakos e H. Hernández-Coronado, Rotossensores quânticos ideais, Phys. Rev.A 95, 052125 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.95.052125

[34] AZ Goldberg e DFV James, Medições de ângulo de Euler limitadas por Quantum usando estados anticoerentes, Phys. Rev. A 98, 032113 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032113

[35] J. Martin, S. Weigert e O. Giraud, Detecção ideal de rotações sobre eixos desconhecidos por estados coerentes e anticoerentes, Quantum 4, 285 (2020).
https:/​/​doi.org/​10.22331/​q-2020-06-22-285

[36] J. Crann, DW Kribs e R. Pereira, Projetos esféricos e estados de spin anticoerentes, J. Phys. R: Matemática. Teoria. 43, 255307 (2010).
https:/​/​doi.org/​10.1088/​1751-8113/​43/​25/​255307

[37] E. Bannai e M. Tagami, Uma nota sobre estados de spin anticoerentes, J. Phys. R: Matemática. Teoria. 44, 342002 (2011).
https:/​/​doi.org/​10.1088/​1751-8113/​44/​34/​342002

[38] M. Wang e Y. Zhu, Estados anticoerentes de spin-2 e projetos esféricos, J. Phys. R: Matemática. Teoria. 55, 425304 (2022).
https://​/​doi.org/​10.1088/​1751-8121/​ac971d

[39] AZ Goldberg, AB Klimov, M.Grassl, G. Leuchs e LL Sánchez-Soto, Estados quânticos extremos, AVS Quantum Sci. 2, 044701 (2020).
https: / / doi.org/ 10.1116 / 5.0025819

[40] AZ Goldberg, M. Grassl, G. Leuchs e LL Sánchez-Soto, Quantumness além do emaranhamento: O caso de estados simétricos, Phys. Rev. A 105, 022433 (2022).
https: / / doi.org/ 10.1103 / PhysRevA.105.022433

[41] O. Giraud, P. Braun e D. Braun, Quantificando a quantumidade e a busca pelas Rainhas da Quântica, New J. Phys. 12, 063005 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​6/​063005

[42] R. Delbourgo, Estados de incerteza mínima para o grupo de rotação e grupos aliados, J. Phys. A10, L233 (1977).
https:/​/​doi.org/​10.1088/​0305-4470/​10/​11/​012

[43] A. Wehrl, Sobre a relação entre entropia clássica e mecânica quântica, Rep. Math. Física. 16, 353 (1979).
https:/​/​doi.org/​10.1016/​0034-4877(79)90070-3

[44] EH Lieb, Prova de uma conjectura de entropia de Wehrl, Commun. Matemática. Física. 62, 35 (1978).
https: / / doi.org/ 10.1007 / BF01940328

[45] CT Lee, entropia dos estados de spin de Wehrl e conjectura de Lieb, J. Phys. A 21, 3749 (1988).
https:/​/​doi.org/​10.1088/​0305-4470/​21/​19/​013

[46] EH Lieb e JP Solovej, Prova de uma conjectura de entropia para estados de spin coerentes de Bloch e suas generalizações, Acta Math. 212, 379 (2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[47] F. Bouchard, at al., Metrologia quântica no limite com constelações extremas de Majorana, Optica 4, 1429-1432 (2017).
https: / / doi.org/ 10.1364 / OPTICA.4.001429

[48] A. Wehrl, Propriedades gerais da entropia, Rev. Mod. Física. 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[49] A. Wehrl, As muitas facetas da entropia, Rep. Math. Física. 30, 119 (1991).
https:/​/​doi.org/​10.1016/​0034-4877(91)90045-O

[50] S. Gnutzmann e K. Życzkowski, entropias de Renyi-Wehrl como medidas de localização no espaço de fase, J. Phys. A 34, 10123 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​47/​317

[51] K. Życzkowski, Localização de estados próprios e entropia média de Wehrl, Physica E 9, 583 (2001).
https:/​/​doi.org/​10.1016/​S1386-9477(00)00266-6

[52] LL Sánchez-Soto, AB Klimov, P. de la Hoz e G. Leuchs, Quantum versus estados de polarização clássicos: quando os multipolos contam, J. Phys. B 46 104011 (2013).
https:/​/​doi.org/​10.1088/​0953-4075/​46/​10/​104011

[53] A. Tavakoli e N. Gisin, Os sólidos platônicos e testes fundamentais da mecânica quântica, Quantum 4, 293 (2020).
https:/​/​doi.org/​10.22331/​q-2020-07-09-293

[54] H. Ch. Nguyen, S. Designolle, M. Barakat e O. Gühne, Simetrias entre medições em mecânica quântica, pré-impressão arXiv:2003.12553 (2022).
https://​/​doi.org/​10.48550/​arXiv.2003.12553
arXiv: 2003.12553

[55] JI Latorre e G. Sierra, emaranhamento platônico, Quantum Inf. Computação. 21, 1081 (2021).
https: / / doi.org/ 10.26421 / QIC21.13-14-1

[56] K. Bolonek-Lasoń e P. Kosiński, Grupos, Sólidos platônicos e desigualdades de Bell, Quantum 5, 593 (2021).
https:/​/​doi.org/​10.22331/​q-2021-11-29-593

[57] KF Pál e T. Vértesi, Grupos, Desigualdades Platônicas de Bell para todas as dimensões, Quantum 6, 756 (2022).
https:/​/​doi.org/​10.22331/​q-2022-07-07-756

[58] RH Dicke, Coerência em processos de radiação espontânea, Phys. 93, 99 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99

[59] V. Karimipour e L. Memarzadeh, Bases equiemaranhadas em dimensões arbitrárias Phys. Rev.A 73, 012329 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.73.012329

[60] G. Rajchel, A. Gąsiorowski e K. Życzkowski, Matrizes robustas de Hadamard, raios unistocásticos em politopo de Birkhoff e bases equi-emaranhadas em espaços compostos Matemática. Comp. Ciência. 12, 473 (2018).
https: / / doi.org/ 10.1007 / s11786-018-0384-y

[61] J. Czartowski, D. Goyeneche, M. Grassl e K. Życzkowski, Bases isoemaranhadas mutuamente imparciais, medições quânticas simétricas e projetos de estado misto, Phys. Rev. 124, 090503 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.124.090503

[62] F. Del Santo, J. Czartowski, K. Życzkowski e N. Gisin, bases iso-emaranhadas e medições conjuntas, pré-impressão arXiv:2307.06998 (2023).
https://​/​doi.org/​10.48550/​arXiv.2307.06998
arXiv: 2307.06998

[63] R. Penrose, On Bell não-localidade sem probabilidades: alguma geometria curiosa, Quantum Reflections (2000).

[64] J. Zimba e R. Penrose, On Bell não-localidade sem probabilidades: Geometria mais curiosa, Stud. História. Fil. Ciência. 24, 697 (1993).
https:/​/​doi.org/​10.1016/​0039-3681(93)90061-N

[65] JE Massad e PK Aravind, O dodecaedro de Penrose revisitado, Am. J. Física 67, 631 (1999).
https: / / doi.org/ 10.1119 / 1.19336

[66] K. Husimi, Algumas propriedades formais da matriz de densidade, Proc. Física. Matemática. Soc. 22, 264 (1940).
https: / / doi.org/ 10.11429 / ppmsj1919.22.4_264

[67] W. Słomczyński e K. Życzkowski, A entropia dinâmica média dos mapas quânticos na esfera diverge no limite semiclássico, Phys. Rev. 80, 1880 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.1880

[68] M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, Transferidores quânticos perfeitos, pré-impressão arXiv:2310.13045 (2023).
https://​/​doi.org/​10.48550/​arXiv.2310.13045
arXiv: 2310.13045

[69] Site NCN Maestro 7 2015/​18/​A/​ST2/​00274 https:/​/​chaos.if.uj.edu.pl/​ karol/​Maestro7/​files/​data3/​Numerical_Results.dat.
https:/​/​chaos.if.uj.edu.pl/​~karol/​Maestro7/​files/​data3/​Numerical_Results.dat

[70] D. Weingarten, Comportamento assintótico de integrais de grupo no limite de classificação infinita, J. Math. Física. 19, 999 (1978).
https: / / doi.org/ 10.1063 / 1.523807

[71] B. Collins e P. Śniady, Integração com respeito à medida Haar em grupo unitário, ortogonal e simplético, Commun. Matemática. Física. 264, 773 (2006).
https:/​/​doi.org/​10.1007/​s00220-006-1554-3

[72] G. Rajchel, Mapeamentos e projetos quânticos, Tese de doutorado, pré-impressão arXiv:2204.13008 (2022).
https://​/​doi.org/​10.48550/​arXiv.2204.13008
arXiv: 2204.13008

[73] D. Martin e EP Wigner, Teoria de grupo e sua aplicação à mecânica quântica de espectros atômicos, Academic Press Inc. NY (1959).
https:/​/​doi.org/​10.1016/​b978-0-12-750550-3.x5001-0

Citado por

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny e Kamil Korzekwa, “Transferidores quânticos perfeitos”, arXiv: 2310.13045, (2023).

[2] Aaron Z. Goldberg, “Correlações para subconjuntos de partículas em estados simétricos: o que os fótons estão fazendo dentro de um feixe de luz quando o resto é ignorado”, arXiv: 2401.05484, (2024).

As citações acima são de SAO / NASA ADS (última atualização com êxito 2024-01-25 11:53:23). A lista pode estar incompleta, pois nem todos os editores fornecem dados de citação adequados e completos.

Não foi possível buscar Dados citados por referência cruzada durante a última tentativa 2024-01-25 11:53:22: Não foi possível buscar os dados citados por 10.22331 / q-2024-01-25-1234 do Crossref. Isso é normal se o DOI foi registrado recentemente.

Este artigo é publicado na Quantum sob o Atribuição 4.0 do Creative Commons Internacional (CC BY 4.0) licença. Os direitos autorais permanecem com os detentores originais, como os autores ou suas instituições.

Carimbo de hora:

Mais de Diário Quântico