The complexity of quantum support vector machines

The complexity of quantum support vector machines

Time Stamp: January 11, 2024 9:08 AM
Source Node: 3057476

Gian Gentinetta1,2, Arne Thomsen3,2, David Sutter2, and Stefan Woerner2

1Institute of Physics, École Polytechnique Fédérale de Lausanne
2IBM Quantum, IBM Research Europe – Zurich
3Department of Physics, ETH Zurich

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

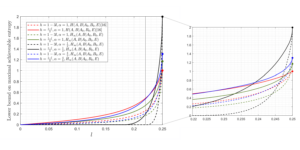
Quantum support vector machines employ quantum circuits to define the kernel function. It has been shown that this approach offers a provable exponential speedup compared to any known classical algorithm for certain data sets. The training of such models corresponds to solving a convex optimization problem either via its primal or dual formulation. Due to the probabilistic nature of quantum mechanics, the training algorithms are affected by statistical uncertainty, which has a major impact on their complexity. We show that the dual problem can be solved in $O(M^{4.67}/varepsilon^2)$ quantum circuit evaluations, where $M$ denotes the size of the data set and $varepsilon$ the solution accuracy compared to the ideal result from exact expectation values, which is only obtainable in theory. We prove under an empirically motivated assumption that the kernelized primal problem can alternatively be solved in $O(min { M^2/varepsilon^6, , 1/varepsilon^{10} })$ evaluations by employing a generalization of a known classical algorithm called Pegasos. Accompanying empirical results demonstrate these analytical complexities to be essentially tight. In addition, we investigate a variational approximation to quantum support vector machines and show that their heuristic training achieves considerably better scaling in our experiments.

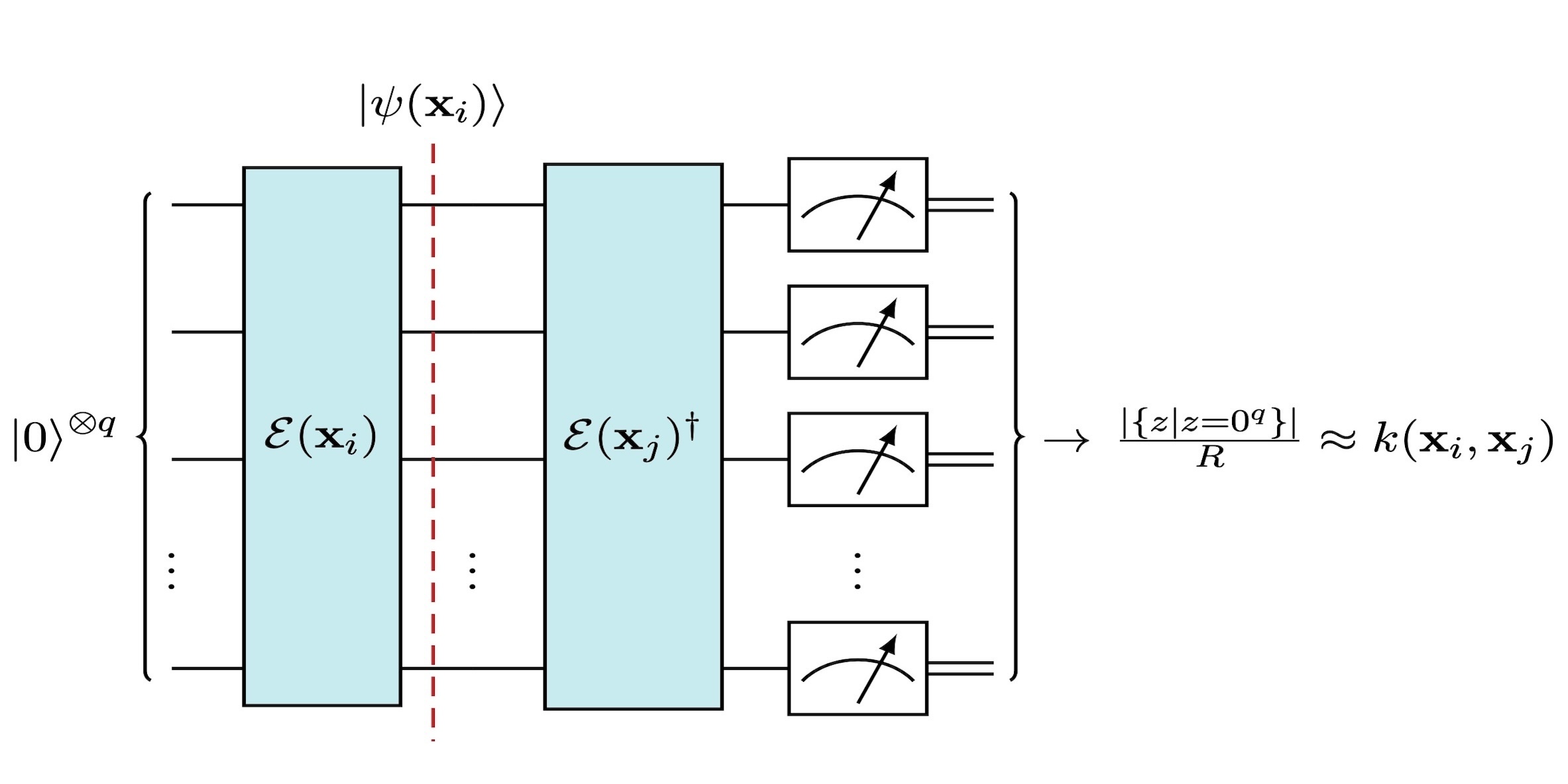
Featured image: Estimation of the kernel value $k(mathbf{x}_i, mathbf{x}_j)$, where $mathcal{E}(mathbf{x}_i)$ denotes a unitary parametrized by the data $mathbf{x}_i$. The number of shots is given by $R$ which controls the accuracy of kernel estimation.

Popular summary

Quantum support vector machines are candidates for demonstrating a quantum advantage in the close future for classification problems. The idea is that a (hopefully useful) kernel function is given by an efficient quantum circuit which is classically hard to evaluate. Due to the probabilistic nature of quantum mechanics such kernel functions are affected by statistical uncertainty. In this work, we rigorously analyze how this uncertainty (also called shot noise) impacts the overall computational complexity for solving the classification problem.

► BibTeX data

► References

[1] J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, and S. Lloyd. Quantum machine learning. Nature, 549(7671):195–202, 2017. DOI: 10.1038/​nature23474.
https:/​/​doi.org/​10.1038/​nature23474

[2] V. Havlíček, A. D. Córcoles, K. Temme, A. W. Harrow, A. Kandala, J. M. Chow, and J. M. Gambetta. Supervised learning with quantum-enhanced feature spaces. Nature, 567(7747):209–212, 2019. DOI: 10.1038/​s41586-019-0980-2.
https:/​/​doi.org/​10.1038/​s41586-019-0980-2

[3] A. Abbas, D. Sutter, C. Zoufal, A. Lucchi, A. Figalli, and S. Woerner. The power of quantum neural networks. Nature Computational Science, 1(June), 2020. DOI: 10.1038/​s43588-021-00084-1.
https:/​/​doi.org/​10.1038/​s43588-021-00084-1

[4] Y. Liu, S. Arunachalam, and K. Temme. A rigorous and robust quantum speed-up in supervised machine learning. Nature Physics, 2021. DOI: 10.1038/​s41567-021-01287-z.
https:/​/​doi.org/​10.1038/​s41567-021-01287-z

[5] S. Aaronson. Read the fine print. Nature Physics, 11(4):291–293, 2015. DOI: 10.1038/​nphys3272.
https:/​/​doi.org/​10.1038/​nphys3272

[6] E. Tang. A quantum-inspired classical algorithm for recommendation systems. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, STOC 2019, page 217–228, New York, NY, USA, 2019. Association for Computing Machinery. DOI: 10.1145/​3313276.3316310.
https:/​/​doi.org/​10.1145/​3313276.3316310

[7] N.-H. Chia, A. Gilyén, T. Li, H.-H. Lin, E. Tang, and C. Wang. Sampling-Based Sublinear Low-Rank Matrix Arithmetic Framework for Dequantizing Quantum Machine Learning, page 387–400. Association for Computing Machinery, New York, NY, USA, 2020. Available online: https:/​/​doi.org/​10.1145/​3357713.3384314.
https:/​/​doi.org/​10.1145/​3357713.3384314

[8] T. Li, S. Chakrabarti, and X. Wu. Sublinear quantum algorithms for training linear and kernel-based classifiers. In International Conference on Machine Learning, pages 3815–3824. PMLR, 2019.

[9] S. Thanasilp, S. Wang, M. Cerezo, and Z. Holmes. Exponential concentration and untrainability in quantum kernel methods, 2022. DOI: 10.48550/​ARXIV.2208.11060.
https:/​/​doi.org/​10.48550/​ARXIV.2208.11060

[10] S. Shalev-Shwartz and N. Srebro. SVM optimization: Inverse dependence on training set size. Proceedings of the 25th International Conference on Machine Learning, pages 928–935, 2008.

[11] A. Thomsen. Comparing quantum neural networks and quantum support vector machines. Master's thesis, ETH Zurich, 2021-09-06. DOI: 20.500.11850/​527559.

[12] B. E. Boser, I. M. Guyon, and V. N. Vapnik. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, COLT '92, pages 144–152, New York, NY, USA, 1992. Association for Computing Machinery. DOI: 10.1145/​130385.130401.
https:/​/​doi.org/​10.1145/​130385.130401

[13] C. Cortes and V. Vapnik. Support-vector networks. In Machine Learning, pages 273–297, 1995.

[14] V. N. Vapnik. The Nature of Statistical Learning Theory. Springer Science+Business Media, LLC, 2000.

[15] F. Pedregosa et al. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research, 12(85):2825–2830, 2011. Available online: http:/​/​jmlr.org/​papers/​v12/​pedregosa11a.html.
http:/​/​jmlr.org/​papers/​v12/​pedregosa11a.html

[16] S. Boyd and L. Vandenberghe. Convex Optimization. Cambridge University Press, 2004.

[17] S. Shalev-Shwartz, Y. Singer, N. Srebro, and A. Cotter. Pegasos: Primal estimated sub-gradient solver for SVM. Mathematical Programming, 127(1):3–30, 2011. DOI: 10.1007/​s10107-010-0420-4.
https:/​/​doi.org/​10.1007/​s10107-010-0420-4

[18] M. D. S. Anis et al. Qiskit: An Open-source Framework for Quantum Computing, 2021. DOI: 10.5281/​zenodo.2573505.
https:/​/​doi.org/​10.5281/​zenodo.2573505

[19] P. Rebentrost, M. Mohseni, and S. Lloyd. Quantum support vector machine for big data classification. Physical Review Letters, 113(3):1–5, 2014. DOI: 10.1103/​PhysRevLett.113.130503.
https:/​/​doi.org/​10.1103/​PhysRevLett.113.130503

[20] J. Kübler, S. Buchholz, and B. Schölkopf. The inductive bias of quantum kernels. In M. Ranzato, A. Beygelzimer, Y. Dauphin, P. Liang, and J. W. Vaughan, editors, Advances in Neural Information Processing Systems, volume 34, pages 12661–12673. Curran Associates, Inc., 2021. Available online: https:/​/​proceedings.neurips.cc/​paper_files/​paper/​2021/​file/​69adc1e107f7f7d035d7baf04342e1ca-Paper.pdf.
https:/​/​proceedings.neurips.cc/​paper_files/​paper/​2021/​file/​69adc1e107f7f7d035d7baf04342e1ca-Paper.pdf

[21] V. Heyraud, Z. Li, Z. Denis, A. Le Boité, and C. Ciuti. Noisy quantum kernel machines. Phys. Rev. A, 106:052421, 2022. DOI: 10.1103/​PhysRevA.106.052421.
https:/​/​doi.org/​10.1103/​PhysRevA.106.052421

[22] C. J. C. Burges and C. J. C. Burges. A Tutorial on Support Vector Machines for Pattern Recognition. Data Mining and Knowledge Discovery, 2:121–167, 1998. Available online: https:/​/​www.microsoft.com/​en-us/​research/​publication/​a-tutorial-on-support-vector-machines-for-pattern-recognition/​.
https:/​/​www.microsoft.com/​en-us/​research/​publication/​a-tutorial-on-support-vector-machines-for-pattern-recognition/​

[23] M. Cerezo, A. Sone, T. Volkoff, L. Cincio, and P. J. Coles. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nature Communications, 12(1):1791, 2021. DOI: 10.1038/​s41467-021-21728-w.
https:/​/​doi.org/​10.1038/​s41467-021-21728-w

[24] Belis, Vasilis, González-Castillo, Samuel, Reissel, Christina, Vallecorsa, Sofia, Combarro, Elías F., Dissertori, Günther, and Reiter, Florentin. Higgs analysis with quantum classifiers. EPJ Web Conf., 251:03070, 2021. DOI: 10.1051/​epjconf/​202125103070.
https:/​/​doi.org/​10.1051/​epjconf/​202125103070

[25] M. Cerezo, A. Arrasmith, R. Babbush, S. C. Benjamin, S. Endo, K. Fujii, J. R. McClean, K. Mitarai, X. Yuan, L. Cincio, and P. J. Coles. Variational quantum algorithms. Nature Reviews Physics, 3(9):625–644, 2021. DOI: 10.1038/​s42254-021-00348-9.
https:/​/​doi.org/​10.1038/​s42254-021-00348-9

[26] R. McGibborn et al. quadprog: Quadratic programming solver (python). https:/​/​github.com/​quadprog/​quadprog, 2022.
https:/​/​github.com/​quadprog/​quadprog

[27] Y. Nesterov. Introductory Lectures on Convex Optimization: A Basic Course. Applied Optimization. Springer, 2004. DOI: 10.1007/​978-1-4419-8853-9.
https:/​/​doi.org/​10.1007/​978-1-4419-8853-9

[28] J. Spall. An Overview of the Simultaneous Perturbation Method for Efficient Optimization. John Hopkins APL Technical Digest, 19(4), pages 482–492, 1998.

[29] G. Gentinetta, A. Thomsen, D. Sutter, and S. Woerner. Code for manuscript ``The complexity of quantum support vector machines". 2022. DOI: https:/​/​doi.org/​10.5281/​zenodo.6303725.
https:/​/​doi.org/​10.5281/​zenodo.6303725

[30] T. Hubregtsen, D. Wierichs, E. Gil-Fuster, P.-J. H. S. Derks, P. K. Faehrmann, and J. J. Meyer. Training quantum embedding kernels on near-term quantum computers. Phys. Rev. A, 106:042431, 2022. DOI: 10.1103/​PhysRevA.106.042431.
https:/​/​doi.org/​10.1103/​PhysRevA.106.042431

[31] R. Latała. Some estimates of norms of random matrices. Proceedings of the American Mathematical Society, 133(5):1273–1282, 2005. DOI: 10.1090/​s0002-9939-04-07800-1.
https:/​/​doi.org/​10.1090/​s0002-9939-04-07800-1

[32] R. Vershynin. Introduction to the non-asymptotic analysis of random matrices. Compressed Sensing: Theory and Applications, pages 210–268, 2009. DOI: 10.1017/​CBO9780511794308.006.
https:/​/​doi.org/​10.1017/​CBO9780511794308.006

[33] T. Hofmann, B. Schölkopf, and A. J. Smola. Kernel methods in machine learning. Annals of Statistics, 36(3):1171–1220, 2008. DOI: 10.1214/​009053607000000677.
https:/​/​doi.org/​10.1214/​009053607000000677

[34] J. W. Daniel. Stability of the solution of definite quadratic programs. Mathematical Programming, 5(1):41–53, 1973. DOI: 10.1007/​BF01580110.
https:/​/​doi.org/​10.1007/​BF01580110

Cited by

[1] Alexander M. Dalzell, Sam McArdle, Mario Berta, Przemyslaw Bienias, Chi-Fang Chen, András Gilyén, Connor T. Hann, Michael J. Kastoryano, Emil T. Khabiboulline, Aleksander Kubica, Grant Salton, Samson Wang, and Fernando G. S. L. Brandão, "Quantum algorithms: A survey of applications and end-to-end complexities", arXiv:2310.03011, (2023).

[2] Maria Schuld and Nathan Killoran, "Is Quantum Advantage the Right Goal for Quantum Machine Learning?", PRX Quantum 3 3, 030101 (2022).

[3] Mohammad Hassan Hassanshahi, Marcin Jastrzebski, Sarah Malik, and Ofer Lahav, "A quantum-enhanced support vector machine for galaxy classification", RAS Techniques and Instruments 2 1, 752 (2023).

[4] Kuan-Cheng Chen, Xiaotian Xu, Henry Makhanov, Hui-Hsuan Chung, and Chen-Yu Liu, "Quantum-Enhanced Support Vector Machine for Large-Scale Stellar Classification with GPU Acceleration", arXiv:2311.12328, (2023).

[5] Supanut Thanasilp, Samson Wang, M. Cerezo, and Zoë Holmes, "Exponential concentration and untrainability in quantum kernel methods", arXiv:2208.11060, (2022).

[6] Kouhei Nakaji, Hiroyuki Tezuka, and Naoki Yamamoto, "Quantum-classical hybrid neural networks in the neural tangent kernel regime", Quantum Science and Technology 9 1, 015022 (2024).

[7] Yaswitha Gujju, Atsushi Matsuo, and Rudy Raymond, "Quantum Machine Learning on Near-Term Quantum Devices: Current State of Supervised and Unsupervised Techniques for Real-World Applications", arXiv:2307.00908, (2023).

[8] Raoul Heese, Thore Gerlach, Sascha Mücke, Sabine Müller, Matthias Jakobs, and Nico Piatkowski, "Explaining Quantum Circuits with Shapley Values: Towards Explainable Quantum Machine Learning", arXiv:2301.09138, (2023).

[9] Julien Gacon, Jannes Nys, Riccardo Rossi, Stefan Woerner, and Giuseppe Carleo, "Variational Quantum Time Evolution without the Quantum Geometric Tensor", arXiv:2303.12839, (2023).

[10] Gian Gentinetta, David Sutter, Christa Zoufal, Bryce Fuller, and Stefan Woerner, "Quantum Kernel Alignment with Stochastic Gradient Descent", arXiv:2304.09899, (2023).

[11] Philippa Duckett, Gabriel Facini, Marcin Jastrzebski, Sarah Malik, Sebastien Rettie, and Tim Scanlon, "Reconstructing charged particle track segments with a quantum-enhanced support vector machine", arXiv:2212.07279, (2022).

[12] Travis L. Scholten, Derrick Perry, Joseph Washington, Jennifer R. Glick, and Thomas Ward, "A Model for Circuit Execution Runtime And Its Implications for Quantum Kernels At Practical Data Set Sizes", arXiv:2307.04980, (2023).

[13] Samantha V. Barron, Daniel J. Egger, Elijah Pelofske, Andreas Bärtschi, Stephan Eidenbenz, Matthis Lehmkuehler, and Stefan Woerner, "Provable bounds for noise-free expectation values computed from noisy samples", arXiv:2312.00733, (2023).

[14] M. Emre Sahin, Benjamin C. B. Symons, Pushpak Pati, Fayyaz Minhas, Declan Millar, Maria Gabrani, Jan Lukas Robertus, and Stefano Mensa, "Efficient Parameter Optimisation for Quantum Kernel Alignment: A Sub-sampling Approach in Variational Training", arXiv:2401.02879, (2024).

The above citations are from SAO/NASA ADS (last updated successfully 2024-01-12 02:12:22). The list may be incomplete as not all publishers provide suitable and complete citation data.

On Crossref's cited-by service no data on citing works was found (last attempt 2024-01-12 02:12:21).

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

Time Stamp:

More from Quantum Journal