Quantum Algorithm For Simulating Hamiltonian Dynamics With An Off-diagonal Series Expansion

Republished By Plato

Followers: 0

Amir Kalev¹ and Itay Hen^2,3

¹Information Sciences Institute, University of Southern California, Arlington, VA 22203, USA
²Information Sciences Institute, University of Southern California, Marina del Rey, CA 90292, USA
³Department of Physics and Astronomy, and Center for Quantum Information Science & Technology,University of Southern California, Los Angeles, California 90089, USA

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

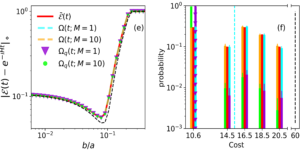
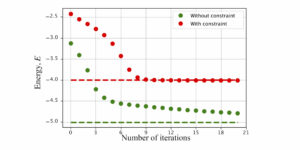
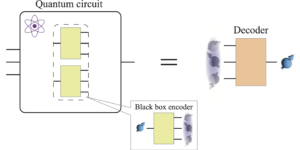
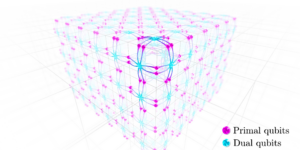
We propose an efficient quantum algorithm for simulating the dynamics of general Hamiltonian systems. Our technique is based on a power series expansion of the time-evolution operator in its off-diagonal terms. The expansion decouples the dynamics due to the diagonal component of the Hamiltonian from the dynamics generated by its off-diagonal part, which we encode using the linear combination of unitaries technique. Our method has an optimal dependence on the desired precision and, as we illustrate, generally requires considerably fewer resources than the current state-of-the-art. We provide an analysis of resource costs for several sample models.

Popular summary

Simulating the dynamics of quantum many-body systems is a central challenge in Physics, Chemistry and the Material Sciences as well as in other areas of science and technology. While for classical algorithms this task is in general intractable, quantum circuits offer a way around the classical bottlenecks by way of `circuitizing’ the time evolution of the system in question. However, present-day quantum computing devices allow for the programming of only small and noisy quantum circuits, a state of matters that places severe constraints on the types of applications these devices may be used for in practice. The qubit and gate costs of circuitization procedures have therefore rightfully become key factors in determining the feasibility of any potential application and increasingly more efficient algorithms are continuously being devised. We propose a novel approach to resource-efficient Hamiltonian dynamics simulations on quantum circuits that we argue offers certain advantages, which directly translate to a shorter algorithm runtime, over state-of-the-art quantum simulation algorithms. We accomplish this by utilizing a series expansion of the quantum time-evolution operator in its off-diagonal elements wherein the operator is expanded around its diagonal component. This expansion allows one to effectively integrate out the diagonal component of the evolution, thereby reducing the overall gate and qubit complexities of the algorithm as compared to existing methods.

► BibTeX data

@article{Kalev2021quantumalgorithm, doi = {10.22331/q-2021-04-08-426}, url = {https://doi.org/10.22331/q-2021-04-08-426}, title = {Quantum {A}lgorithm for {S}imulating {H}amiltonian {D}ynamics with an {O}ff-diagonal {S}eries {E}xpansion}, author = {Kalev, Amir and Hen, Itay}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {5}, pages = {426}, month = apr, year = {2021}<br /> }

► References

[1] D. W. Berry, A. M. Childs, R. Cleve, R. Kothari, and R. D. Somma. Simulating hamiltonian dynamics with a truncated taylor series. Phys. Rev. Lett., 114: 090502, Mar 2015. https://doi.org/10.1103/PhysRevLett.114.090502.
https://doi.org/10.1103/PhysRevLett.114.090502

[2] G. Hao Low and N. Wiebe. Hamiltonian Simulation in the Interaction Picture. arXiv e-prints, art. arXiv:1805.00675, May 2018.
arXiv:1805.00675

[3] T. Albash, G. Wagenbreth, and I. Hen. Off-diagonal expansion quantum monte carlo. Phys. Rev. E, 96: 063309, Dec 2017. https://doi.org/10.1103/PhysRevE.96.063309.
https://doi.org/10.1103/PhysRevE.96.063309

[4] I. Hen. Off-diagonal series expansion for quantum partition functions. Journal of Statistical Mechanics: Theory and Experiment, 2018 (5): 053102, 2018. https://doi.org/10.1088/1742-5468/aabbe4.
https://doi.org/10.1088/1742-5468/aabbe4

[5] L. Gupta, T. Albash, and I. Hen. Permutation matrix representation quantum monte carlo. Journal of Statistical Mechanics: Theory and Experiment, 2020 (7): 073105, jul 2020a. https://doi.org/10.1088/1742-5468/ab9e64.
https://doi.org/10.1088/1742-5468/ab9e64

[6] Y.-H. Chen, A. Kalev, and I. Hen. A quantum algorithm for time-dependent Hamiltonian simulation by permutation expansion. arXiv e-prints, art. arXiv:2103.15334, March 2021.
arXiv:2103.15334

[7] E. T. Whittaker and G. Robinson. Divided differences. In The Calculus of Observations: A Treatise on Numerical Mathematics. New York: Dover, New York, 1967.

[8] C. de Boor. Divided differences. Surveys in Approximation Theory, 1: 46–69, 2005. https://arxiv.org/abs/math/0502036.
https://arxiv.org/abs/math/0502036

[9] M. A. Nielsen and I. L. Chuang. Quantum Computation and Quantum Information. Cambridge University Press, USA, 10th edition, 2011. ISBN 1107002176.

[10] R. M. Corless, G. H. Gonnet, D. E. G. Hare, D. J. Jeffrey, and D. E. Knuth. On the lambertw function. Advances in Computational Mathematics, 5 (1): 329–359, Dec 1996. ISSN 1572-9044. https://doi.org/10.1007/BF02124750.
https://doi.org/10.1007/BF02124750

[11] V. V. Shende, S. S. Bullock, and I. L. Markov. Synthesis of quantum-logic circuits. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 25 (6): 1000–1010, 2006. https://doi.org/10.1109/TCAD.2005.855930.
https://doi.org/10.1109/TCAD.2005.855930

[12] A. Barenco, C. H. Bennett, R. Cleve, D. P. DiVincenzo, N. Margolus, P. Shor, T. Sleator, J. A. Smolin, and H. Weinfurter. Elementary gates for quantum computation. Phys. Rev. A, 52: 3457–3467, Nov 1995. https://doi.org/10.1103/PhysRevA.52.3457.
https://doi.org/10.1103/PhysRevA.52.3457

[13] A. Kalev and I. Hen. An integral-free representation of the Dyson series using divided differences. arXiv e-prints, art. arXiv:2010.09888, October 2020.
arXiv:2010.09888

[14] J. Hubbard and B. H. Flowers. Electron correlations in narrow energy bands. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 276 (1365): 238–257, 1963. https://doi.org/10.1098/rspa.1963.0204.
https://doi.org/10.1098/rspa.1963.0204

[15] A. Tranter, P. J. Love, F. Mintert, and P. V. Coveney. A comparison of the bravyi-kitaev and jordan-wigner transformations for the quantum simulation of quantum chemistry. Journal of chemical theory and computation, 14 (11): 5617–5630, 11 2018. https://doi.org/10.1021/acs.jctc.8b00450.
https://doi.org/10.1021/acs.jctc.8b00450

[16] S. B. Bravyi and A. Yu. Kitaev. Fermionic quantum computation. Annals of Physics, 298 (1): 210 – 226, 2002. ISSN 0003-4916. https://doi.org/10.1006/aphy.2002.6254.
https://doi.org/10.1006/aphy.2002.6254

[17] F. Verstraete and J. I. Cirac. Mapping local hamiltonians of fermions to local hamiltonians of spins. Journal of Statistical Mechanics: Theory and Experiment, 2005 (09): P09012–P09012, sep 2005. https://doi.org/10.1088/1742-5468/2005/09/p09012.
https://doi.org/10.1088/1742-5468/2005/09/p09012

[18] C. Derby and J. Klassen. A Compact Fermion to Qubit Mapping. arXiv e-prints, art. arXiv:2003.06939, March 2020.
arXiv:2003.06939

[19] R. Babbush, N. Wiebe, J. McClean, J. McClain, H. Neven, and G. K.-L. Chan. Low-depth quantum simulation of materials. Phys. Rev. X, 8: 011044, Mar 2018. https://doi.org/10.1103/PhysRevX.8.011044.
https://doi.org/10.1103/PhysRevX.8.011044

[20] J. Schwinger. Gauge invariance and mass. ii. Phys. Rev., 128: 2425–2429, Dec 1962. https://doi.org/10.1103/PhysRev.128.2425.
https://doi.org/10.1103/PhysRev.128.2425

[21] Z. Davoudi, M. Hafezi, C. Monroe, G. Pagano, A. Seif, and A. Shaw. Towards analog quantum simulations of lattice gauge theories with trapped ions. Phys. Rev. Research, 2: 023015, Apr 2020. https://doi.org/10.1103/PhysRevResearch.2.023015.
https://doi.org/10.1103/PhysRevResearch.2.023015

[22] J. Kogut and L. Susskind. Hamiltonian formulation of wilson’s lattice gauge theories. Phys. Rev. D, 11: 395–408, Jan 1975. https://doi.org/10.1103/PhysRevD.11.395.
https://doi.org/10.1103/PhysRevD.11.395

[23] T. Banks, L. Susskind, and J. Kogut. Strong-coupling calculations of lattice gauge theories: (1 + 1)-dimensional exercises. Phys. Rev. D, 13: 1043–1053, Feb 1976. https://doi.org/10.1103/PhysRevD.13.1043.
https://doi.org/10.1103/PhysRevD.13.1043

[24] E. Rieffel and W. Polak. Quantum Computing: A Gentle Introduction. MIT Press, Cambridge, MA, 2011.

[25] L. Gupta, L. Barash, and I. Hen. Calculating the divided differences of the exponential function by addition and removal of inputs. Computer Physics Communications, 254: 107385, 2020b. ISSN 0010-4655. https://doi.org/10.1016/j.cpc.2020.107385.
https://doi.org/10.1016/j.cpc.2020.107385

[26] T. Häner, M. Roetteler, and K. M. Svore. Optimizing Quantum Circuits for Arithmetic. arXiv e-prints, art. arXiv:1805.12445, May 2018.
arXiv:1805.12445

Cited by

[1] Amir Kalev and Itay Hen, “An integral-free representation of the Dyson series using divided differences”, arXiv:2010.09888.

[2] Yi-Hsiang Chen, Amir Kalev, and Itay Hen, “A quantum algorithm for time-dependent Hamiltonian simulation by permutation expansion”, arXiv:2103.15334.

[3] Efekan Kökcü, Thomas Steckmann, J. K. Freericks, Eugene F. Dumitrescu, and Alexander F. Kemper, “Fixed Depth Hamiltonian Simulation via Cartan Decomposition”, arXiv:2104.00728.

The above citations are from SAO/NASA ADS (last updated successfully 2021-04-10 13:00:28). The list may be incomplete as not all publishers provide suitable and complete citation data.

On Crossref’s cited-by service no data on citing works was found (last attempt 2021-04-10 13:00:26).

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

Source: https://quantum-journal.org/papers/q-2021-04-08-426/

Time Stamp: April 8, 2021

Quantum Algorithm for Simulating Hamiltonian Dynamics with an Off-diagonal Series Expansion

Republished By Plato

Abstract

Popular summary

► BibTeX data

► References

Cited by

More from Quantum Journal

Importance sampling for stochastic quantum simulations

Measurement disturbance and conservation laws in quantum mechanics

Universal construction of decoders from encoding black boxes

Concatenation Schemes for Topological Fault-tolerant Quantum Error Correction

Digital Discovery of 100 diverse Quantum Experiments with PyTheus

Certifying the quantum Fisher information from a given set of mean values: a semidefinite programming approach

Quantum Local Search with the Quantum Alternating Operator Ansatz

Quantum reference frames: derivation of perspective-dependent descriptions via a perspective-neutral structure

Limits of Short-Time Evolution of Local Hamiltonians

Optimal nonequilibrium thermometry in Markovian environments

About Us

Vertical Search & Ai

Platform

Stay Connected

Account