Vitalik Buterin przez Blog Vitalika Buterina
To jest lustrzane odbicie postu pod adresem https://medium.com/@VitalikButerin/programy-arytmetyczne-kwadratowe-od-zera-do-bohatera-f6d558cea649
Ostatnio pojawiło się duże zainteresowanie technologią stojącą za zk-SNARK, a ludzi coraz więcej próbując zdemistyfikować coś, co wielu zaczęło nazywać „matematyką księżycową” ze względu na jej postrzeganą niemożliwą do rozszyfrowania złożoność. Zk-SNARK rzeczywiście są dość trudne do zrozumienia, szczególnie ze względu na ogromną liczbę ruchomych części, które muszą się połączyć, aby całość działała, ale jeśli rozłożymy technologię na kawałki, zrozumienie stanie się prostsze.
Celem tego wpisu nie jest pełne wprowadzenie do zk-SNARK; zakłada jako wiedzę podstawową, że (i) wiesz, czym są zk-SNARK i do czego służą oraz (ii) znasz wystarczająco dużo matematyki, aby móc wyciągać wnioski na temat takich rzeczy jak wielomiany (jeśli stwierdzenie �(�)+�(�) =(�+�)(�) , gdzie � i � są wielomianami, wydaje Ci się to naturalne i oczywiste, to jesteś na właściwym poziomie). W poście autorzy zagłębiają się raczej w mechanizmy stojące za technologią i starają się jak najlepiej wyjaśnić pierwszą połowę rurociągu, jak narysował tutaj Eran Tromer, badacz zk-SNARK:

Kroki tutaj można podzielić na dwie połowy. Po pierwsze, zk-SNARK nie można zastosować bezpośrednio do żadnego problemu obliczeniowego; raczej musisz przekształcić problem w odpowiednią „formę”, aby można było na nim działać. Formularz nazywa się „kwadratowym programem arytmetycznym” (QAP), a przekształcenie kodu funkcji w jeden z nich jest samo w sobie wysoce nietrywialne. Wraz z procesem konwersji kodu funkcji do QAP istnieje inny proces, który można uruchomić równolegle, dzięki czemu, jeśli masz dane wejściowe do kodu, możesz stworzyć odpowiednie rozwiązanie (czasami nazywane „świadkiem” QAP). Następnie następuje kolejny dość skomplikowany proces tworzenia faktycznego „dowodu z wiedzą zerową” dla tego świadka oraz oddzielny proces weryfikacji dowodu, który przekazuje Ci ktoś inny, ale są to szczegóły, które nie mieszczą się w tym poście .
Przykład, który wybierzemy, jest prosty: udowodnienie, że znasz rozwiązanie równania sześciennego: �3+�+5=35 (wskazówka: odpowiedź brzmi 3). Problem ten jest na tyle prosty, że wynikowy QAP nie będzie tak duży, aby zastraszał, ale na tyle nietrywialny, że będzie można zobaczyć, jak wszystkie mechanizmy wchodzą w grę.
Zapiszmy naszą funkcję w następujący sposób:
def qeval(x):
y = x**3
return x + y + 5Prosty język programowania specjalnego przeznaczenia, którego tutaj używamy, obsługuje podstawową arytmetykę (+, -, ⋅, /), potęgowanie o stałej mocy (�7, ale nie ��) i przypisywanie zmiennych, co jest na tyle potężne, że teoretycznie możesz to zrobić dowolne obliczenia w nim zawarte (o ile liczba kroków obliczeniowych jest ograniczona; pętle nie są dozwolone). Zauważ, że operatory modulo (%) i operatory porównania (<, >, ≤, ≥) NIE są obsługiwane, ponieważ nie ma skutecznego sposobu na wykonanie modulo lub porównania bezpośrednio w arytmetyce skończonych grup cyklicznych (bądź za to wdzięczny; gdyby był sposób zrobić jedno i drugie, wówczas kryptografia krzywych eliptycznych zostałaby złamana szybciej, niż można powiedzieć „wyszukiwanie binarne” i „chińskie twierdzenie o resztach”).
Możesz rozszerzyć język na modulo i porównania, dostarczając rozkłady bitów (np. 13=23+22+1) jako wejścia pomocnicze, udowadniając poprawność tych rozkładów i wykonując obliczenia w obwodach binarnych; w arytmetyce pól skończonych sprawdzanie równości (==) jest również wykonalne i w rzeczywistości nieco łatwiejsze, ale są to oba szczegóły, którymi nie będziemy się teraz zajmować. Możemy rozszerzyć język, aby obsługiwał warunki warunkowe (np. if �<5:�=7; else: �=9), konwertując je do postaci arytmetycznej: �=7⋅(�<5)+9⋅(�≥5 ), jednak pamiętaj, że obie „ścieżki” warunku warunkowego musiałyby zostać wykonane, a jeśli masz wiele zagnieżdżonych warunków warunkowych, może to prowadzić do dużych kosztów ogólnych.
Przeanalizujmy teraz ten proces krok po kroku. Jeśli chcesz to zrobić samodzielnie dla dowolnego fragmentu kodu, I zaimplementowałem tutaj kompilator (wyłącznie do celów edukacyjnych; nie jest jeszcze gotowy do tworzenia QAP dla rzeczywistych zk-SNARK!).
Spłaszczenie
Pierwszym krokiem jest procedura „spłaszczania”, podczas której konwertujemy oryginalny kod, który może zawierać dowolnie złożone instrukcje i wyrażenia, na ciąg instrukcji występujących w dwóch postaciach: �=� (gdzie � może być zmienną lub liczbą ) i �=� (��) � (gdzie �� może oznaczać +, −, ⋅, / oraz � i � mogą być zmiennymi, liczbami lub same w sobie podwyrażeniami). Każde z tych stwierdzeń można traktować jako coś w rodzaju bramek logicznych w obwodzie. Wynik procesu spłaszczania powyższego kodu jest następujący:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5Jeśli przeczytasz oryginalny kod i kod tutaj, możesz dość łatwo zobaczyć, że oba są równoważne.
Bramy do R1CS
Teraz przekształcamy to w coś, co nazywa się systemem ograniczeń rangi 1 (R1CS). R1CS to ciąg grup trzech wektorów (�, �, �), a rozwiązaniem R1CS jest wektor �, gdzie � musi spełniać równanie �.�⋅�.�−�.�=0, gdzie . reprezentuje iloczyn skalarny – mówiąc prościej, jeśli „spinamy razem” � i �, mnożąc dwie wartości w tych samych pozycjach, a następnie sumujemy te iloczyny, następnie robimy to samo z � i �, a następnie � i � , wówczas trzeci wynik jest iloczynem dwóch pierwszych wyników. Na przykład jest to zadowolony R1CS:
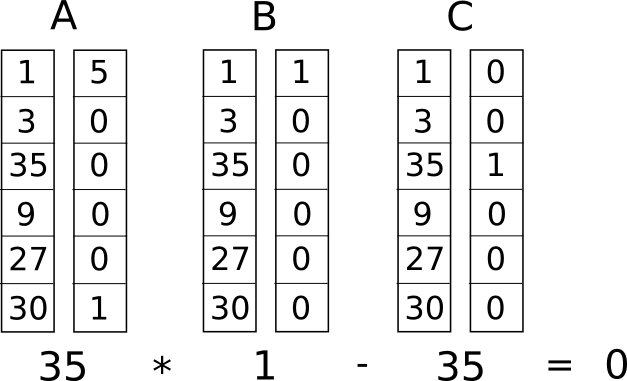
Zamiast jednak mieć tylko jedno ograniczenie, będziemy mieć wiele ograniczeń: po jednym dla każdej bramki logicznej. Istnieje standardowy sposób konwertowania bramki logicznej na trójkę (�,�,�) w zależności od tego, jaka to operacja (+, −, ⋅ lub /) i czy argumenty są zmiennymi czy liczbami. Długość każdego wektora jest równa całkowitej liczbie zmiennych w systemie, włączając zmienną fikcyjną ~jeden w pierwszym indeksie reprezentującą liczbę 1, zmienne wejściowe, zmienną fikcyjną ~out reprezentującą wynik, a następnie wszystkie zmienne pośrednie (���1 i ���2 powyżej); wektory będą na ogół bardzo rzadkie, wypełniając jedynie szczeliny odpowiadające zmiennym, na które wpływa jakaś konkretna bramka logiczna.
Najpierw udostępnimy mapowanie zmiennych, którego będziemy używać:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'Wektor rozwiązania będzie się składał z przypisań dla wszystkich tych zmiennych w tej kolejności.
Teraz podamy potrójną (�,�,�) dla pierwszej bramki:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Widać, że jeśli wektor rozwiązania zawiera 3 na drugiej pozycji i 9 na czwartej pozycji, to niezależnie od reszty zawartości wektora rozwiązania, sprawdzenie iloczynu skalarnego sprowadzi się do 3⋅3=9 i więc to minie. Jeśli wektor rozwiązania ma -3 na drugiej pozycji i 9 na czwartej pozycji, sprawdzenie również zakończy się pomyślnie; w rzeczywistości, jeśli wektor rozwiązania ma 7 na drugiej pozycji i 49 na czwartej pozycji, to sprawdzenie nadal będzie pozytywne — celem tej pierwszej kontroli jest sprawdzenie spójności wejść i wyjść tylko pierwszej bramki.
Przejdźmy teraz do drugiej bramy:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]W podobny sposób jak w przypadku pierwszego sprawdzania iloczynu kropkowego, tutaj sprawdzamy, czy ���1⋅�=�.
A teraz trzecia brama:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]Tutaj wzór jest nieco inny: mnoży pierwszy element wektora rozwiązania przez drugi element, następnie przez piąty element, dodając oba wyniki i sprawdzając, czy suma jest równa szóstemu elementowi. Ponieważ pierwszym elementem wektora rozwiązania jest zawsze jeden, jest to tylko sprawdzenie dodawania polegające na sprawdzeniu, czy wynik jest równy sumie dwóch wejść.
Wreszcie czwarta brama:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]Tutaj oceniamy ostatnie sprawdzenie, ~out =���2+5. Sprawdzanie iloczynu skalarnego polega na wzięciu szóstego elementu wektora rozwiązania, dodaniu pięciokrotności pierwszego elementu (przypomnienie: pierwszy element to 1, więc w rzeczywistości oznacza to dodanie 5) i porównaniu go z trzecim elementem, czyli w tym miejscu zapisz zmienną wyjściową.
I tam mamy nasz R1CS z czterema ograniczeniami. Świadkiem jest po prostu przypisanie do wszystkich zmiennych, włączając w to zmienne wejściowe, wyjściowe i wewnętrzne:
[1, 3, 35, 9, 27, 30]Możesz to obliczyć samodzielnie, po prostu „wykonując” powyższy spłaszczony kod, zaczynając od przypisania zmiennej wejściowej �=3 i wprowadzając wartości wszystkich zmiennych pośrednich oraz dane wyjściowe podczas ich obliczania.
Kompletny zestaw R1CS to:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]R1CS do QAP
Następnym krokiem jest wzięcie tego R1CS i przekształcenie go w formę QAP, która implementuje dokładnie tę samą logikę, z wyjątkiem użycia wielomianów zamiast iloczynów skalarnych. Robimy to w następujący sposób. Przechodzimy do 3 z czterech grup trzech wektorów o długości od sześciu do sześciu grup wielomianów trzech stopnia-3, gdzie oceniamy wielomiany w każdym współrzędna x reprezentuje jedno z ograniczeń. Oznacza to, że jeśli obliczymy wielomiany w punkcie �=1, otrzymamy pierwszy zbiór wektorów, jeśli obliczymy wielomiany w punkcie �=2, otrzymamy drugi zbiór wektorów i tak dalej.
Możemy dokonać tej transformacji za pomocą czegoś, co nazywa się a Interpolacja Lagrange'a. Problem rozwiązywany przez interpolację Lagrange'a jest następujący: jeśli masz zbiór punktów (tj. (�,�) par współrzędnych), to wykonanie interpolacji Lagrange'a na tych punktach daje wielomian przechodzący przez wszystkie te punkty. Robimy to poprzez dekompozycję problemu: dla każdej współrzędnej � tworzymy wielomian, który ma pożądaną współrzędną � w tej współrzędnej � i współrzędną � równą 0 we wszystkich pozostałych interesujących nas współrzędnych, a następnie otrzymujemy ostateczną W rezultacie dodajemy wszystkie wielomiany do siebie.
Zróbmy przykład. Załóżmy, że chcemy wielomianu przechodzącego przez (1,3), (2,2) i (3,4). Zaczynamy od stworzenia wielomianu przechodzącego przez (1,3), (2,0) i (3,0). Jak się okazuje, utworzenie wielomianu, który „wystaje” w punkcie �=1 i ma wartość zero w pozostałych punktach zainteresowania, jest łatwe; po prostu robimy:
(x - 2) * (x - 3)Wygląda to tak:
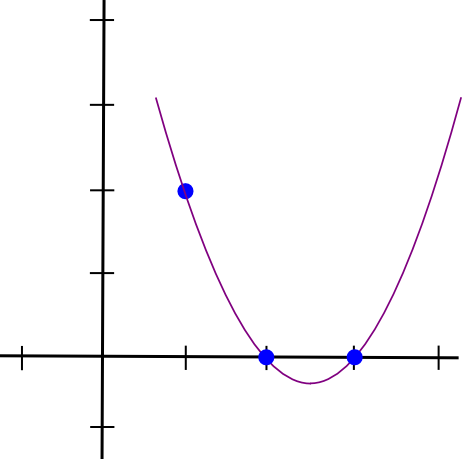
Teraz musimy tylko „przeskalować” go tak, aby wysokość przy x=1 była właściwa:
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))To daje nam:
1.5 * x**2 - 7.5 * x + 9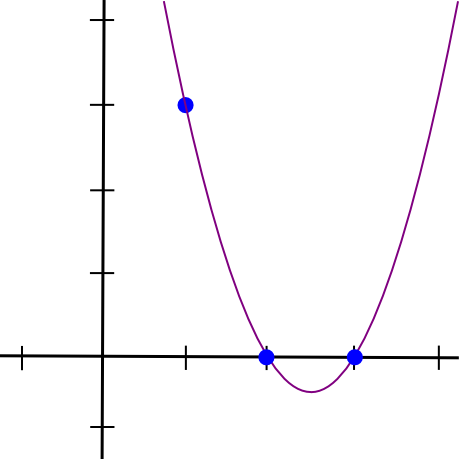
Następnie robimy to samo z dwoma pozostałymi punktami i otrzymujemy dwa inne podobnie wyglądające wielomiany, z tą różnicą, że „wystają” w �=2 i �=3 zamiast �=1. Dodajemy wszystkie trzy razem i otrzymujemy:
1.5 * x**2 - 5.5 * x + 7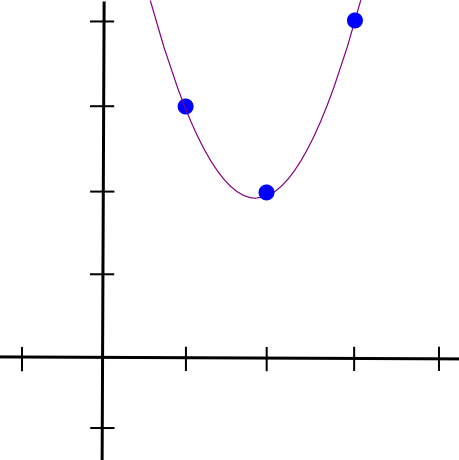
Z dokładnie takimi współrzędnymi, jakie chcemy. Algorytm opisany powyżej zajmuje �(�3) czasu, ponieważ jest � punktów, a każdy punkt wymaga �(�2) czasu na pomnożenie wielomianów przez siebie; przy odrobinie myślenia można to zredukować do czasu �(�2), a przy dużo większym myśleniu, stosując algorytmy szybkiej transformacji Fouriera i tym podobne, można to skrócić jeszcze bardziej — kluczowa optymalizacja, gdy funkcje używane w zk -SNARK w praktyce często ma wiele tysięcy bramek.
Teraz użyjmy interpolacji Lagrange'a, aby przekształcić nasz R1CS. Zamierzamy pobrać pierwszą wartość z każdego wektora �, użyć interpolacji Lagrange'a, aby utworzyć z tego wielomian (gdzie obliczenie wielomianu w � daje pierwszą wartość wektora �-tego �), powtórzyć proces dla pierwszej wartości każdego wektora � i �, a następnie powtórz ten proces dla drugich wartości, trzecich, wartości i tak dalej. Dla ułatwienia podam odpowiedzi już teraz:
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]Współczynniki są uporządkowane rosnąco, więc pierwszy wielomian powyżej ma w rzeczywistości wartość 0.833⋅�3—5⋅�2+9.166⋅�−5. Ten zbiór wielomianów (plus wielomian Z, który wyjaśnię później) tworzy parametry dla tej konkretnej instancji QAP. Zauważ, że całą pracę do tego momentu należy wykonać tylko raz dla każdej funkcji, którą próbujesz zweryfikować za pomocą zk-SNARK; po wygenerowaniu parametrów QAP można je ponownie wykorzystać.
Spróbujmy ocenić wszystkie te wielomiany przy �=1. Ocena wielomianu przy �=1 oznacza po prostu zsumowanie wszystkich współczynników (jako 1�=1 dla wszystkich �), więc nie jest to trudne. Otrzymujemy:
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0I oto, co tu mamy, jest dokładnie takie samo, jak zbiór trzech wektorów dla pierwszej bramki logicznej, który stworzyliśmy powyżej.
Sprawdzanie QAP
Jaki jest sens tej szalonej transformacji? Odpowiedź jest taka, że zamiast sprawdzać ograniczenia w R1CS indywidualnie, możemy teraz to sprawdzić wszystkie ograniczenia jednocześnie wykonując kontrolę iloczynu skalarnego na wielomianach.
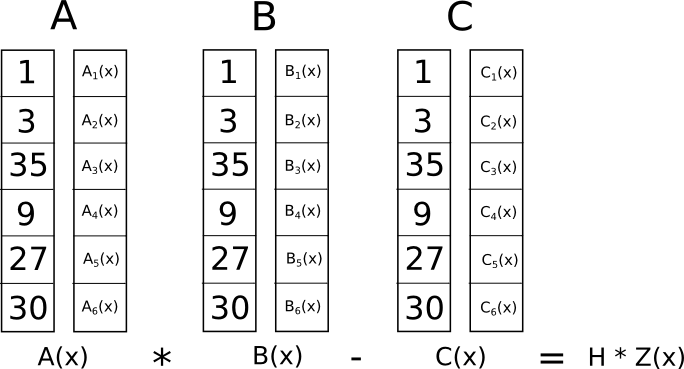
Ponieważ w tym przypadku sprawdzanie iloczynu skalarnego polega na serii dodawania i mnożenia wielomianów, wynik sam w sobie będzie wielomianem. Jeśli wynikowy wielomian, obliczony przy każdej współrzędnej �, której użyliśmy powyżej do przedstawienia bramki logicznej, jest równy zeru, oznacza to, że wszystkie kontrole zakończyły się pomyślnie; jeśli wynikowy wielomian obliczony na co najmniej jednej ze współrzędnych � reprezentujących bramkę logiczną daje wartość różną od zera, oznacza to, że wartości wchodzące i wychodzące z tej bramki logicznej są niespójne (tj. bramka ma wartość �=�⋅�� �1, ale podane wartości mogą wynosić �=2,���1=2 i �=5).
Należy zauważyć, że powstały wielomian sam w sobie nie musi wynosić zero i w większości przypadków tak nie będzie; może zachowywać się w dowolny sposób w punktach, które nie odpowiadają żadnej bramce logicznej, o ile wynik wynosi zero we wszystkich punktach, które do odpowiadają jakiejś bramie. Aby sprawdzić poprawność, tak naprawdę nie oceniamy wielomianu �=�.�⋅�.�−�.� w każdym punkcie odpowiadającym bramce; zamiast tego dzielimy � przez inny wielomian � i sprawdzamy, czy � dzieli równomiernie � – to znaczy, że dzielenie �/� nie pozostawia reszty.
� definiuje się jako (�−1)⋅(�−2)⋅(�−3)… – najprostszy wielomian równy zeru we wszystkich punktach odpowiadających bramkom logicznym. Jest to elementarny fakt algebry każdy wielomian równy zero we wszystkich tych punktach musi być wielokrotnością tego minimalnego wielomianu, a jeśli wielomian jest wielokrotnością �, to jego ocena w którymkolwiek z tych punktów będzie wynosić zero; ta równoważność znacznie ułatwia nam pracę.
Teraz przeprowadźmy sprawdzenie iloczynu skalarnego za pomocą powyższych wielomianów. Najpierw wielomiany pośrednie:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]Teraz �.�⋅�.�—�.�:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Teraz minimalny wielomian �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):
Z = [24, -50, 35, -10, 1]A jeśli podzielimy powyższy wynik przez �, otrzymamy:
h = t / Z = [-3.666, 17.055, -3.444]Bez reszty.
I tak mamy rozwiązanie dla QAP. Jeśli spróbujemy sfałszować którąkolwiek ze zmiennych w rozwiązaniu R1CS, z którego wyprowadzamy rozwiązanie QAP — powiedzmy, ustawmy ostatnią na 31 zamiast 30, wówczas otrzymamy wielomian �, który nie przejdzie żadnej kontroli (w tym konkretnym w tym przypadku wynik przy �=3 będzie równy −1 zamiast 0), a ponadto � nie będzie wielokrotnością �; raczej dzielenie �/� dałoby resztę [−5.0,8.833, −4.5,0.666].
Należy pamiętać, że powyższe jest uproszczeniem; „w prawdziwym świecie” dodawanie, mnożenie, odejmowanie i dzielenie nie będą zachodzić w przypadku liczb regularnych, ale raczej w przypadku skończonych elementów ciała — jest to przerażający rodzaj arytmetyki, który jest samowystarczalny, więc wszystkie prawa algebraiczne, które znamy i kochamy nadal jest prawdziwe, ale gdzie wszystkie odpowiedzi są elementami pewnego zbioru o skończonych rozmiarach, zwykle są to liczby całkowite z zakresu od 0 do �−1 dla niektórych �. Na przykład, jeśli �=13, to 1/2=7 (oraz 7⋅2=1), 3⋅5=2 i tak dalej. Stosowanie arytmetyki pola skończonego eliminuje potrzebę martwienia się o błędy zaokrągleń i pozwala systemowi dobrze pracować z krzywymi eliptycznymi, które w efekcie są niezbędne dla reszty maszynerii zk-SNARK, dzięki czemu protokół zk-SNARK jest faktycznie bezpieczny.
Specjalne podziękowania dla Erana Tromera za pomoc w wyjaśnieniu mi wielu szczegółów dotyczących wewnętrznego działania zk-SNARK.
- Dystrybucja treści i PR oparta na SEO. Uzyskaj wzmocnienie już dziś.
- PlatoData.Network Pionowe generatywne AI. Wzmocnij się. Dostęp tutaj.
- PlatoAiStream. Inteligencja Web3. Wiedza wzmocniona. Dostęp tutaj.
- PlatonESG. Węgiel Czysta technologia, Energia, Środowisko, Słoneczny, Gospodarowanie odpadami. Dostęp tutaj.
- Platon Zdrowie. Inteligencja w zakresie biotechnologii i badań klinicznych. Dostęp tutaj.
- Przesunięcia bloków. Modernizacja własności offsetu środowiskowego. Dostęp tutaj.
- Źródło: Inteligencja danych Platona.
