En kunstig intelligens-basert løsning på Sudoku

29. januar er National Puzzle Day, og for å feire det, har vi laget en morsom blogg som beskriver hvordan du løser Sudoku ved hjelp av kunstig intelligens (AI).

Introduksjon

Før Wordleden Sudoku puslespill var raseriet, og det er fortsatt veldig populært. De siste årene har bruken av optimalisering metoder for å løse gåten har vært et dominerende tema. Se "Løse Sudoku-puslespill ved hjelp av optimalisering i Arkieva".

I dagens tid er bruken av AI fokusert på maskinlæring som omfatter et bredt spekter av metoder fra lasso-regresjon til forsterkende læring. Bruken av AI har dukket opp igjen å takle komplekse planlegging utfordringer. En metode, søk med tilbakesporing, er ofte brukt og er perfekt for Sudoku.

Denne bloggen vil gi en detaljert beskrivelse av hvordan du bruker denne metoden for å løse Sudoku. Som det viser seg, kan "backtracking" finnes i optimaliserings- og maskinlæringsmotorer og er en hjørnestein i den avanserte heuristikken Arkieva bruker for planlegging. Algoritmen er implementert i et "Array Programming Language", et funksjonsorientert programmeringsspråk som håndterer en rikt sett med array-strukturer.

Grunnleggende om Sudoku

Fra Wikipedia: Sudoku er et logikkbasert, kombinatorisk tallplasseringspuslespill. Målet er å fylle et 9×9 rutenett med sifre slik at hver kolonne, hver rad og hver av de ni 3×3 underrutene som utgjør rutenettet (også kalt "bokser", "blokker", "regioner", eller "sub-kvadrater") inneholder alle sifrene fra 1 til 9. Puslespillet gir et delvis fullført rutenett, som vanligvis har en unik løsning. Fullførte oppgaver er alltid en type latinsk firkant med en ekstra begrensning på innholdet i individuelle regioner. For eksempel kan det samme enkelt heltall ikke vises to ganger i den samme 9×9-spillebrettraden eller -kolonnen eller i noen av de ni 3×3-underregionene på 9×9-spillebrettet.

Tabell 1 har et eksempelproblem. Det er 9 rader og 9 kolonner for totalt 81 celler. Hver har lov til å ha ett og bare ett av ni heltall mellom 1 og 9. I startløsningen har en celle enten en enkelt verdi – som fikserer verdien i denne cellen til den verdien, eller cellen er tom, noe som indikerer at vi trenger for å finne en verdi for denne cellen. Cellen (1,1) har verdien 2 og celle (6,5) har verdien 6. Celle (1,2) og celle (2,3) er tomme, og algoritmen vil finne en verdi for disse cellene.

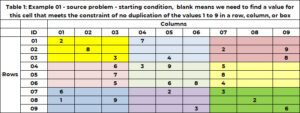
Komplikasjonen

I tillegg til å tilhøre én og bare én rad og kolonne, tilhører en celle én og kun én boks. Det er 1 bokser, og de er angitt med farge i tabell 9. Tabell 1 bruker et unikt heltall mellom 2 og 1 for å identifisere hver boks eller rutenett. Cellene med en radverdi på (9, 1 eller 2) og kolonneverdi på (3, 1 eller 2) tilhører boks 3. Boks 1 er radverdier på (6, 4, 5) og kolonneverdier (6, 7) , 8). Boks-IDen bestemmes av formelen BOX_ID = {9x(gulv((ROW_ID-3) /1)} + tak (COL_ID/3). For cellen (3), 5,7 = 6x(gulv(3-5) ))/1) + tak (3/8)= 3×3 + 1 = 3+3.

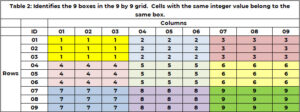
Hjertet av puslespillet

Å finne en heltallsverdi mellom 1 og 9 for hver ukjent celle slik at heltallene 1 til 9 brukes én gang og bare én gang for hver kolonne, hver rad og hver boks.

La oss se på celle (1,3) som er tom. Rad 1 har allerede verdiene 2 og 7. Disse er ikke tillatt i denne cellen. Kolonne 3 har allerede verdiene 3, 5,6, 7,9. Disse er ikke tillatt. Boks 1 (gul) har verdiene 2, 3 og 8. Disse er ikke tillatt. Følgende verdier er ikke tillatt (2,7); (3, 5, 6, 7, 9); (2, 3, 8). De unike verdiene som ikke er tillatt er (2, 3, 5, 6, 7, 8, 9). De eneste kandidatverdiene er (1,4).

En løsningsmetode ville være å midlertidig tildele 1 til celle (1,3) og deretter prøve å finne kandidatverdier for en annen celle.

En tilbakesporingsløsning: Starte komponenter

Array struktur

Utgangspunktet er å bestemme seg for en matrisestruktur for å lagre kildeproblemet og støtte søket. Tabell 3 har denne array-strukturen. Kolonne 1 er en unik heltalls-ID for hver celle. Verdiene varierer fra 1 til 81. Kolonne 2 er rad-ID-en til cellen. Kolonne 3 er kolonne-ID-en til cellen. Kolonne 4 er boks-ID. Kolonne 5 er verdien i cellen. Observer at en celle uten verdi får verdien null i stedet for blank eller null. Dette holder dette en "bare heltallsarray" - langt overlegen for ytelse.

I APL vil denne matrisen bli lagret i en 2-dimensjonal matrise der formen er 81 x 5. Anta at elementene i Tabell 3 er lagret i variabelen MAT. Eksempelfunksjoner er:

Kommandoen MAT[1 2 3;] tar tak i de første 3 radene med MAT
1 1 1 1 2
2 1 2 1 0
3 1 3 1 0
MAT[1 2 3; 4 5] sikrer rad 1, 2, 3 og bare kolonne 4 og 5
1 2
1 0
1 0
(MAT[;5]=0)/MAT[;1] finner alle celler som trenger en verdi.

SETTE INN TABELL 3

Sanity Check: Duplikater

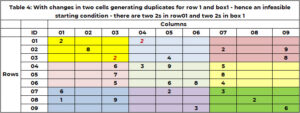
Før du starter søket, er det viktig å sjekke fornuften! Det er startløsningen som er mulig. Gjennomførbart for Sudoku, er det nå duplikater i en hvilken som helst rad, kolonne eller boks. Dagens startløsning, for eksempel 1, er gjennomførbar. Tabell 4 har et eksempel hvor startløsningen har duplikater. Rad 1 har to verdier 2. Område 1 har to verdier 2. Funksjonen "SANITY_DUPE" håndterer denne logikken.

Sanity Check: Alternativer for celler uten verdier

En svært nyttig informasjon vil være alle mulige verdier for en celle uten verdi. Hvis det ikke er noen kandidater, er dette puslespillet ikke løsbart. En celle kan ikke ta på seg en verdi som allerede er gjort krav på av naboen. Ved å bruke tabell 1 for celle (1,3,'1' – denne siste 1 er boks), dens naboer er rad 1, kolonne 3 og boks 1. Rad 1 har verdiene (2,7); kolonne 3 har verdiene (3,5,6,7,9); boks 1 har verdiene (2,3,8). Celle (1,3.1) kan ikke ta følgende verdier (2,3,5,6,7,8,9). De eneste alternativene for celle (1,3,1) er (1,4). For celle (4,1,2) er verdiene 1, 2, 3, 5, 6, 7, 9 allerede brukt i rad 4, kolonne 1 og/eller boks 4. De eneste kandidatverdiene er (4,8) . Unction "SANITY_CAND" håndterer denne logikken.

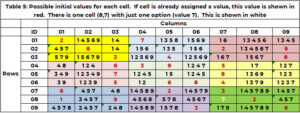
Tabell 5 viser kandidatene, for eksempel 1 ved starten av søkeprosessen. Hvis en celle allerede har blitt tildelt en verdi i startbetingelsene (tabell 1), gjentas denne verdien og vises i rødt. Hvis en celle som trenger en verdi bare har ett alternativ, vises dette i hvitt. Celle (8,7,9) har enkeltverdien 7 i hvitt. (2,5,8,4,3) er hevdet av nabokolonne 7. (1, 2, 9) av rad 8. (3,2,6) av boks 9. Bare verdien 7 er ikke gjort krav på.

Sanity Check: Leter etter konflikter

Informasjonen som identifiserer alle alternativer for celler som trenger en verdi (oppgitt i tabell 4), gjør det mulig for oss å identifisere en konflikt før du starter søkeprosessen. En konflikt oppstår når to celler som trenger en verdi bare har én kandidat, kandidatverdien er den samme, og de to cellene er naboer. Fra tabell 4 vet vi at den eneste cellen som trenger en verdi og bare har én kandidat er celle (8,7,9). For eksempel 1, det er ingen konflikt.

Hva ville være en konflikt? Hvis den eneste mulige verdien for celle (3,7,3) var 7 (i stedet for 1, 6, 7), så er det en konflikt. Celle (8,7) og celle (3,7) er naboer – samme kolonne. Men hvis den eneste mulige verdien for celle (4,9,2) var 7 (i stedet for 1, 2, 7), ville dette ikke være en konflikt. Disse cellene er ikke naboer.

Sammendrag av helsesjekk

1. Hvis det er duplikater, er startløsningen ikke gjennomførbar.
2. Hvis en celle som trenger en verdi, ikke har noen kandidater, er det ingen mulig løsning på dette puslespillet. Listen over kandidatverdier for hver celle kan brukes til å redusere søkeområdet – både for tilbakesporing og optimalisering.
3. Evnen til å finne konflikter identifiserer at gåten ikke er gjennomførbar – har ingen løsning – uten en søkeprosess. I tillegg identifiserer den "problemcellene".

En tilbakesporingsløsning: Søkeprosess

Med kjernedatastrukturer og helsekontroll på plass, retter vi oppmerksomheten mot søkeprosessen. Det tilbakevendende temaet er igjen, å få på plass datastrukturer for å støtte søk.

Sporing av søket

Matrisen Tracker holder styr på oppdragene som er gjort

1. Kol 1 er telleren
2. Kol 2 er antallet alternativer som er tilgjengelige for å tildele denne cellen
   • 1 betyr 1 alternativ tilgjengelig, 2 betyr to alternativer osv.
   • 0 betyr – ingen alternativ tilgjengelig eller tilbakestilling til 0 (ingen tilordnet verdi) og tilbakesporing
3. Kol 3 er cellen som er tildelt et verdiindeksnummer (1 til 81)
4. Kol 4 er verdien som er tildelt cellen i sporhistorikken
   • En verdi på 9999 betyr at denne cellen var da blindveien ble funnet
   • Verdien av et heltall mellom 1 og 9 inklusive, er den tildelte verdien til denne cellen på dette tidspunktet i søkeprosessen.
   • En verdi på 0 betyr at denne cellen trenger en tilordning

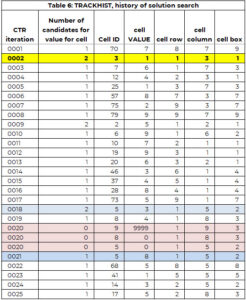
Tracker-arrayet brukes til å støtte søkeprosessen. Matrisen SPORHIST har samme struktur som trackeren, men beholder historien til hele søkeprosessen. Tabell 6 har en del av TRACKHIST for eksempel 1. Det er forklart mer detaljert i et senere avsnitt.

I tillegg arrayen PAV (en vektor av en vektor), holder styr på tidligere tildelte verdier til denne cellen. Dette sikrer at vi ikke går tilbake til en mislykket løsning – i likhet med det som gjøres i TABU.

Det er en valgfri loggprosess der søkeprosessen skriver ut hvert trinn.

Starter søket

Med bokføring og helsekontroll utført, kan vi nå starte søkeprosessen. Fremgangsmåten er:

1. Er det noen celler igjen som trenger en verdi? – hvis nei, så er vi ferdige.
2. For hver celle som trenger en verdi, finn alle kandidatalternativer for hver celle. Tabell 4 har disse verdiene ved starten av løsningsprosessen. Ved hver iterasjon oppdateres dette for å imøtekomme verdier som er tildelt celler.
3. Vurder alternativene i denne rekkefølgen.
   • Hvis en celle har NULL alternativer, så initier tilbakesporing
   • Finn alle cellene med ett alternativ, velg en av disse cellene, lag denne oppgaven,
     1. og oppdater sporingstabellen, gjeldende løsning og PAV.
   • Hvis alle cellene har mer enn ett alternativ, velg én celle og én verdi, og oppdater
     1. og oppdater sporingstabellen, gjeldende løsning og PAV

Vi vil bruke Tabell 6 som er en del av historien til løsningsprosessen (kalt TRACKHIST) for å illustrere hvert trinn.

I den første iterasjonen (CTR=1), er celle 70 (rad 8, kolonne 7, boks 9) valgt for å bli tildelt en verdi. Det er bare kandidat (7), og denne verdien tildeles celle 70. I tillegg legges verdien 7 til vektoren av tidligere tildelte verdier (PAV) for celle 70.

I den andre iterasjonen er cellen 30 tildelt verdien 1. Denne cellen hadde to kandidatverdier. Den minste kandidatverdien tildeles cellen (bare en vilkårlig regel for å gjøre logikken enkel å følge).

Prosessen med å identifisere en celle som trenger en verdi og tildele en verdi fungerer fint inntil iterasjon (CTR) 20. Celle 9 trenger verdi, men antallet kandidater er NULL. Det er to alternativer:

• Det er ingen løsning på dette puslespillet.
• Vi angrer (backtrack) noen av oppgavene og tar en annen vei.

Vi lette etter celleoppgaven nærmest denne, der det var mer enn ett alternativ. I dette eksemplet skjedde dette ved iterasjon 18, der celle 5 er tildelt verdien 3, men det var to kandidatverdier for celle 5 – verdier 3 og 8.

Mellom celle 5 (CTR = 18) og celle 9 (CTR = 20), er celle 8 tildelt verdien 4 (CTR=19). Vi setter celle 8 og 5 tilbake på listen "trenger en verdi". Dette fanges opp i andre og tredje CTR=20-oppføringer, der verdien settes til 0. Verdien 3 beholdes i PAV-vektoren for celle 5. Det vil si at søkemotoren ikke kan tilordne verdien 3 til celle 5.

Søkemotoren starter opp igjen for å identifisere en verdi for celle 5 (med 3 ikke lenger et alternativ) og tildeler verdien 8 til celle 5 (CTR=21). Det fortsetter til alle cellene har en verdi eller det er en celle uten alternativ og det ikke er noen tilbakesporingsbane. Løsningen er lagt ut i tabell 7.

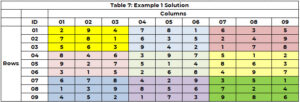
Vær oppmerksom på at der det er mer enn én kandidat for en celle, er dette en sjanse for parallell behandling.

Sammenligning med MILP Optimization Solution

På overflatenivå er representasjonen av Sudoku-puslespillet dramatisk annerledes. AI-tilnærmingen bruker heltall og er, uansett mål, en strammere og mer intuitiv representasjon. I tillegg gir fornuftskontrollene nyttig informasjon for å lage en sterkere formulering. MILP-representasjonen er uendelig binærfiler (0/1). Imidlertid er binærfilene kraftige representasjoner gitt styrken til moderne MILP-løsere.

Internt beholder ikke MILP-løseren binærfilene, men bruker en sparse array-metode for å eliminere lagring av alle nullene. I tillegg dukker ikke algoritmene for å løse binære filer opp før på 1980- og 1990-tallet. Avisen fra 1983 av Crowder, Johnson og Padberg rapporter om en av de første praktiske løsningene for optimalisering med binærfiler. De bemerker viktigheten av smart forbehandling og gren- og bindingsmetoder som avgjørende for en vellykket løsning.

Den nylige eksplosjonen av bruk av begrensningsprogrammering og programvare som f.eks lokal løser har gjort det klart viktigheten av å bruke AI-metoder med de originale optimaliseringsmetodene som lineær programmering og minste kvadrater.

• SEO-drevet innhold og PR-distribusjon. Bli forsterket i dag.
• PlatoData.Network Vertical Generative Ai. Styrk deg selv. Tilgang her.
• PlatoAiStream. Web3 Intelligence. Kunnskap forsterket. Tilgang her.
• PlatoESG. Karbon, CleanTech, Energi, Miljø, Solenergi, Avfallshåndtering. Tilgang her.
• PlatoHelse. Bioteknologisk og klinisk etterretning. Tilgang her.
• kilde: https://blog.arkieva.com/an-artificial-intelligence-based-solution-to-sudoku/?utm_source=rss&utm_medium=rss&utm_campaign=an-artificial-intelligence-based-solution-to-sudoku