Orthonormale basis van extreme kwantumheid

Orthonormale basis van extreme kwantumheid

Tijdstempel: 25 januari 2024 6:51 uur
Bronknooppunt: 3083690

Marcin Rudziński1,2, Adam Burchardt3 en Karol Zyczkowski1,4

1Faculteit Natuurkunde, Sterrenkunde en Toegepaste Computerwetenschappen, Jagiellonian University, ul. Łojasiewicza 11, 30-348 Kraków, Polen
2Doctorale School voor Exacte en Natuurwetenschappen, Jagiellonian Universiteit, ul. Łojasiewicza 11, 30-348 Krakau, Polen
3QuSoft, CWI en Universiteit van Amsterdam, Science Park 123, 1098 XG Amsterdam, Nederland
4Centrum voor theoretische fysica, Poolse Academie van Wetenschappen, Al. Lotników 32/46, 02-668 Warszawa, Polen

Vind je dit artikel interessant of wil je het bespreken? Scite of laat een reactie achter op SciRate.

Abstract

Spin-anticoherente toestanden hebben de laatste tijd veel aandacht gekregen als de meest “kwantum”-toestanden. Sommige coherente en anticoherente spintoestanden staan ​​bekend als optimale kwantumrotosensoren. In dit werk introduceren we een maatstaf voor kwantumheid voor orthonormale bases van spintoestanden, bepaald door de gemiddelde anticoherentie van individuele vectoren en de Wehrl-entropie. Op deze manier identificeren we de meest coherente en meest kwantumtoestanden, die leiden tot orthogonale metingen van extreme kwantumheid. Hun symmetrieën kunnen worden onthuld met behulp van de Majorana-stellaire representatie, die een intuïtieve geometrische representatie biedt van een zuivere toestand door punten op een bol. De verkregen resultaten leiden tot maximaal (minimaal) verstrengelde basen in de $2j+1$ dimensionale symmetrische deelruimte van de $2^{2j}$ dimensionale ruimte van toestanden van meerdelige systemen bestaande uit $2j$ qubits. Sommige gevonden basen zijn iso-coherent omdat ze bestaan ​​uit alle toestanden met dezelfde mate van spin-coherentie.

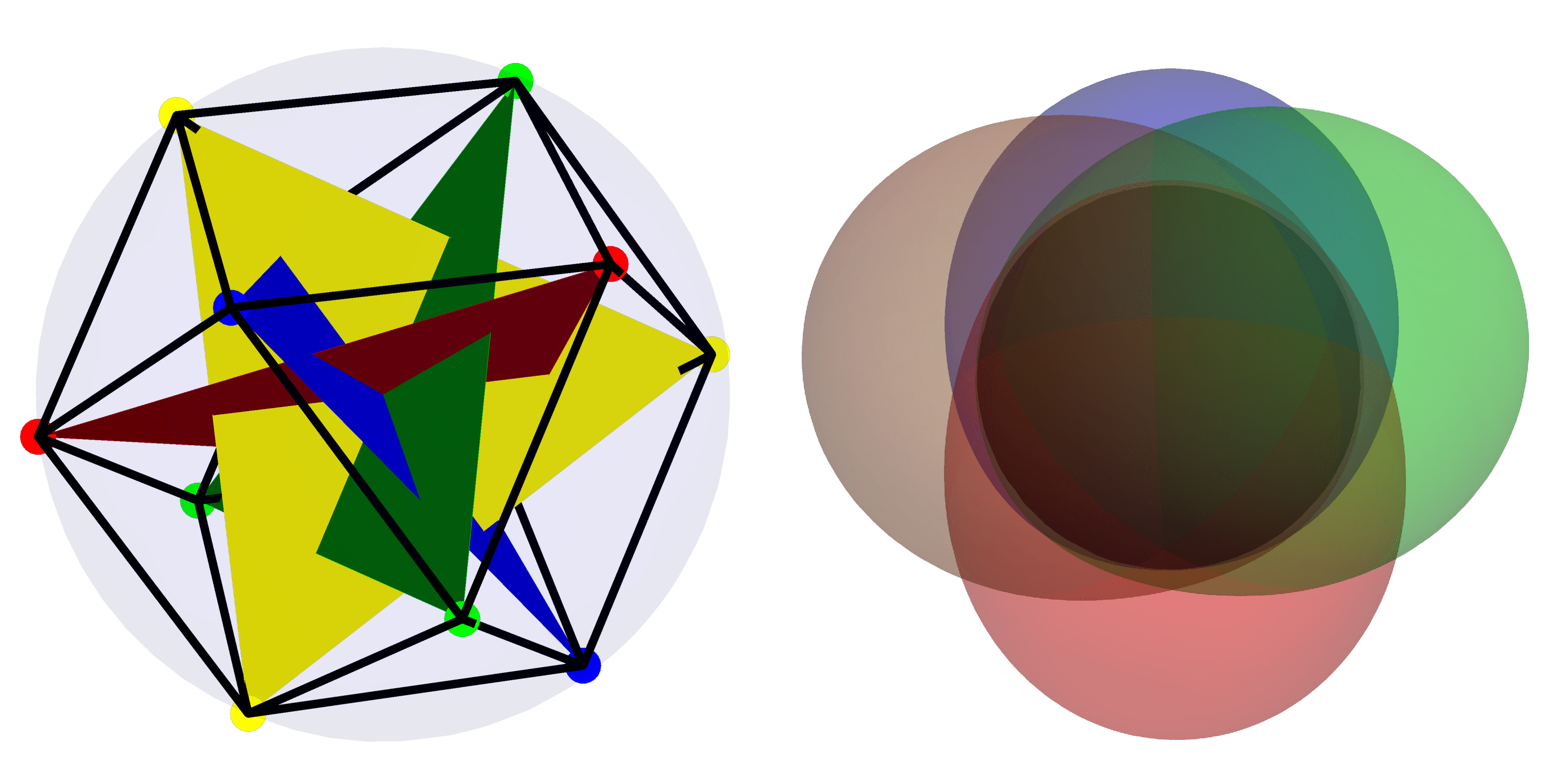
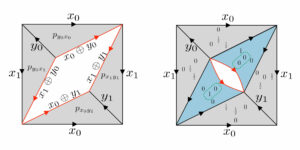
Uitgelichte afbeelding: In de linkerafbeelding wordt de meest ‘kwantumbasis’ in $mathcal{H}_4$ weergegeven met behulp van de stellaire representatie. Aan de rechterkant wordt de Husimi-functie voor staten op de meest coherente (“klassieke”) basis binnen $mathcal{H}_4$ weergegeven.

Populaire samenvatting

Extremal states, coherent and anticoherent, have practical applications in quantum metrology as optimal rotosensors. This work provides a natural extension of previous studies concerning the search for such states proposing optimal orthogonal measurements of Lüders and von Neumann of the extreme spin coherence. We introduce the measure $mathcal{B}_t$ as the tool to characterize the quantumness of a measurement given by a basis in $mathcal{H}_N$. The search for the most quantum bases for $N=3,4,5$ and $7$ is performed. Numerical results suggest, that the obtained solutions are unique. A set of candidates for the “classical” bases consisting of the most spin-coherent states is indicated for $N=3,4,5,6$. Some of the most quantum bases, analyzed in the stellar representation of Majorana, reveal symmetries of Platonic solids. Most classical bases display symmetric structures too. We also considered other measures of the quantumness of vectors forming a given basis. Optimization of the mean Wehrl entropy of $N$ orthogonal vectors leads to the same bases distinguished by extremal values of the quantities $mathcal{B}_t$, with a single exception of the quantum basis for $N=6$.

► BibTeX-gegevens

► Referenties

[1] T. Frankel, The Geometry of Physics: An Introduction, 3e ed., Cambridge University Press (2011).
https: / / doi.org/ 10.1017 / CBO9781139061377

[2] D. Chruściński en A. Jamiołkowski, Geometrische fasen in klassieke en kwantummechanica, Birkhäuser (2004).
https:/​/​doi.org/​10.1007/​978-0-8176-8176-0

[3] DA Lee, Geometrische relativiteitstheorie, American Mathematical Society, Providence (2021).
https: / / doi.org/ 10.1090 / gsm / 201

[4] I. Bengtsson en K. Życzkowski, Geometry of Quantum States: An Introduction to Quantum Entanglement, 2e ed., Cambridge University Press (2017).
https: / / doi.org/ 10.1017 / 9781139207010

[5] M. Lewin, Geometrische methoden voor niet-lineaire kwantumsystemen met veel deeltjes, J. Functional Analysis 260, 12, (2011).
https: / / doi.org/ 10.1016 / j.jfa.2010.11.017

[6] E. Cohen, H. Larocque, F. Bouchard et al., Geometrische fase van Aharonov-Bohm tot Pancharatnam-Berry en verder, Nat. Ds. Phys. 1, 437–449 (2019).
https:/​/​doi.org/​10.1038/​s42254-019-0071-1

[7] E. Majorana Atomi orientati in campo magnetische variabele, Nuovo Cimento 9, 43-50 (1932).
https: / / doi.org/ 10.1007 / BF02960953

[8] R. Barnett, A. Turner en E. Demler, Classificatie van nieuwe fasen van spinoratomen, Phys. Ds. Lett. 97, 180412 (2006).
https: / / doi.org/ 10.1103 / PhysRevLett.97.180412

[9] R. Barnett, A. Turner en E. Demler, Classificatie van wervels in $ S = 3 $ Bose-Einstein-condensaten, Phys. Rev.A 76, 013605 (2007).
https: / / doi.org/ 10.1103 / PhysRevA.76.013605

[10] H. Mäkelä, en K.-A. Suominen, Inerte toestanden van spin-s-systemen, Phys. Ds. Lett. 99, 190408 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.190408

[11] E. Serrano-Ensástiga en F. Mireles, Fasekarakterisering van spinor Bose-Einstein-condensaten: een Majorana-stellaire representatiebenadering, Phys. Let. A492, 129188 (2023).
https: / / doi.org/ 10.1016 / j.physleta.2023.129188

[12] P. Mathonet et al., Verstrengelingsequivalentie van $N$-qubit symmetrische toestanden, Phys. Rev.A 81, 052315 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.052315

[13] J. Martin, O. Giraud, PA Braun, D. Braun en T. Bastin, Multiqubit symmetrische staten met hoge geometrische verstrengeling, Phys. Rev.A 81, 062347 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.062347

[14] M. Aulbach, DJH Markham en M. Murao, De maximaal verstrengelde symmetrische toestand in termen van de geometrische maat, New J. Phys. 12, 073025 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​7/​073025

[15] DJH Markham, Verstrengeling en symmetrie in permutatie-symmetrische toestanden, Phys. Rev.A 83, 042332 (2011).
https: / / doi.org/ 10.1103 / PhysRevA.83.042332

[16] P. Ribeiro en R. Mosseri, Verstrengeling in de symmetrische sector van $n$ qubits, Phys. Ds. Lett. 106, 180502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.106.180502

[17] M.Aulbach, Classificatie van verstrengeling in symmetrische toestanden, Int. J. Quantum Inform. 10, 1230004 (2012).
https: / / doi.org/ 10.1142 / S0219749912300045

[18] W. Ganczarek, M. Kuś en K. Życzkowski, Barycentrische maatstaf voor kwantumverstrengeling, Phys. Rev.A 85, 032314 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.032314

[19] A. Mandilara, T. Coudreau, A. Keller en P. Milman, Verstrengelingsclassificatie van puur symmetrische toestanden via spin-coherente toestanden, Phys. Rev.A 90, 050302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.050302

[20] P. Hyllus, et al., Fisher information and multiparticle entanglement, Phys. Rev.A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[21] JH Hannay, De Berry-fase voor spin in de Majorana-voorstelling, J. Phys. EEN: Wiskunde. Gen. 31, L53 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​2/​002

[22] P. Bruno, Kwantumgeometrische fase in Majorana's stellaire representatie: in kaart brengen op een Aharonov-Bohm-fase met meerdere lichamen, Phys. Ds. Lett. 108, 240402 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.240402

[23] HD Liu en LB Fu, Berry-fase en kwantumverstrengeling in Majorana's stellaire representatie, Phys. Rev.A 94, 022123 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.022123

[24] P. Ribeiro, J. Vidal en R. Mosseri, Thermodynamische limiet van het Lipkin-Meshkov-Glick-model, Phys. Ds. Lett. 99, 050402 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.050402

[25] P. Ribeiro, J. Vidal en R. Mosseri, Exact spectrum van het Lipkin-Meshkov-Glick-model in de thermodynamische limiet en eindige groottecorrecties, Phys. E 78, 021106 (2008).
https: / / doi.org/ 10.1103 / PhysRevE.78.021106

[26] J. Zimba, “Anticoherente” spin-staten via de Majorana-vertegenwoordiging, Electron. J. Theor. Fys. 3, 143 (2006).
https://​/​api.semanticscholar.org/​CorpusID:13938120

[27] D. Baguette, T. Bastin en J. Martin, Multiqubit-symmetrische toestanden met maximaal gemengde one-qubit-reducties, Phys. Rev. A 90, 032314 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.032314

[28] O. Giraud, D. Braun, D. Baguette, T. Bastin, en J. Martin, Tensor-representatie van spintoestanden, Phys. Rev. Lett. 114, 080401 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.080401

[29] D. Baguette, F. Damanet, O. Giraud en J. Martin, anticoherentie van spintoestanden met puntgroepsymmetrieën, Phys. Rev.A 92, 052333 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.92.052333

[30] HD Liu, LB Fu, X. Wang, Coherent-state benadering voor Majorana-vertegenwoordiging, Commun. Theor. Fys. 67, 611 (2017).
https:/​/​doi.org/​10.1088/​0253-6102/​67/​6/​611

[31] D. Baguette en J. Martin, Anticoherentiemaatregelen voor zuivere spintoestanden, Phys. Rev.A 96, 032304 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.032304

[32] P. Kolenderski en R. Demkowicz-Dobrzański, Optimale staat voor het op één lijn houden van referentieframes en de platonische lichamen, Phys. Rev.A 78, 052333 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052333

[33] C. Chryssomalakos en H. Hernández-Coronado, Optimale kwantumrotosensoren, Phys. A 95, 052125 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.95.052125

[34] AZ Goldberg en DFV James, Quantum-gelimiteerde Euler-hoekmetingen met behulp van anticoherente toestanden, Phys. Rev.A 98, 032113 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032113

[35] J. Martin, S. Weigert en O. Giraud, Optimale detectie van rotaties rond onbekende assen door coherente en anticoherente toestanden, Quantum 4, 285 (2020).
https:/​/​doi.org/​10.22331/​q-2020-06-22-285

[36] J. Crann, DW Kribs en R. Pereira, sferische ontwerpen en anticoherente spinstaten, J. Phys. EEN: Wiskunde. Theor. 43, 255307 (2010).
https:/​/​doi.org/​10.1088/​1751-8113/​43/​25/​255307

[37] E. Bannai en M. Tagami, Een opmerking over anticoherente spintoestanden, J. Phys. EEN: Wiskunde. Theor. 44, 342002 (2011).
https:/​/​doi.org/​10.1088/​1751-8113/​44/​34/​342002

[38] M. Wang en Y. Zhu, anticoherente spin-2-staten en bolvormige ontwerpen, J. Phys. EEN: Wiskunde. Theor. 55, 425304 (2022).
https://​/​doi.org/​10.1088/​1751-8121/​ac971d

[39] AZ Goldberg, AB Klimov, M.Grassl, G. Leuchs en LL Sánchez-Soto, Extremale kwantumtoestanden, AVS Quantum Sci. 2, 044701 (2020).
https: / / doi.org/ 10.1116 / 5.0025819

[40] AZ Goldberg, M. Grassl, G. Leuchs en LL Sánchez-Soto, Quantumness voorbij verstrengeling: het geval van symmetrische toestanden, Phys. A 105, 022433 (2022).
https: / / doi.org/ 10.1103 / PhysRevA.105.022433

[41] O. Giraud, P. Braun en D. Braun, Kwantificering van kwantumheid en de zoektocht naar Queens of Quantum, New J. Phys. 12, 063005 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​6/​063005

[42] R. Delbourgo, Minimale onzekerheidstoestanden voor de rotatiegroep en aanverwante groepen, J. Phys. A10, L233 (1977).
https:/​/​doi.org/​10.1088/​0305-4470/​10/​11/​012

[43] A. Wehrl, Over de relatie tussen klassieke en kwantummechanische entropie, Rep. Math. Fys. 16, 353 (1979).
https:/​/​doi.org/​10.1016/​0034-4877(79)90070-3

[44] EH Lieb, Bewijs van een entropievermoeden van Wehrl, Commun. Wiskunde. Fys. 62, 35 (1978).
https: / / doi.org/ 10.1007 / BF01940328

[45] CT Lee, Wehrl's entropie van spintoestanden en het vermoeden van Lieb, J. Phys. A21, 3749 (1988).
https:/​/​doi.org/​10.1088/​0305-4470/​21/​19/​013

[46] EH Lieb en JP Solovej, Bewijs van een entropievermoeden voor Bloch-coherente spintoestanden en de generalisaties ervan, Acta Math. 212, 379 (2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[47] F. Bouchard, et al., Kwantummetrologie aan de limiet met extreme Majorana-sterrenbeelden, Optica 4, 1429-1432 (2017).
https: / / doi.org/ 10.1364 / OPTICA.4.001429

[48] A. Wehrl, Algemene eigenschappen van entropie, Rev. Mod. Fys. 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[49] A. Wehrl, De vele facetten van entropie, Rep. Math. Fys. 30, 119 (1991).
https:/​/​doi.org/​10.1016/​0034-4877(91)90045-O

[50] S. Gnutzmann en K. Życzkowski, Renyi-Wehrl-entropieën als maatstaven voor lokalisatie in faseruimte, J. Phys. A34, 10123 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​47/​317

[51] K. Życzkowski, Lokalisatie van eigentoestanden en gemiddelde Wehrl-entropie, Physica E 9, 583 (2001).
https:/​/​doi.org/​10.1016/​S1386-9477(00)00266-6

[52] LL Sánchez-Soto, AB Klimov, P. de la Hoz en G. Leuchs, Quantum versus klassieke polarisatietoestanden: wanneer multipolen tellen, J. Phys. B46 104011 (2013).
https:/​/​doi.org/​10.1088/​0953-4075/​46/​10/​104011

[53] A. Tavakoli en N. Gisin, The Platonische lichamen en fundamentele tests van de kwantummechanica, Quantum 4, 293 (2020).
https:/​/​doi.org/​10.22331/​q-2020-07-09-293

[54] H. Ch. Nguyen, S. Designolle, M. Barakat en O. Gühne, Symmetrieën tussen metingen in de kwantummechanica, voordruk arXiv:2003.12553 (2022).
https:/​/​doi.org/​10.48550/​arXiv.2003.12553
arXiv: 2003.12553

[55] JI Latorre en G. Sierra, Platonische verstrengeling, Quantum Inf. Computer. 21, 1081 (2021).
https: / / doi.org/ 10.26421 / QIC21.13-14-1

[56] K. Bolonek-Lasoń en P. Kosiński, Groepen, Platonische lichamen en Bell-ongelijkheid, Quantum 5, 593 (2021).
https:/​/​doi.org/​10.22331/​q-2021-11-29-593

[57] KF Pál en T. Vértesi, Groups, Platonic Bell-ongelijkheid voor alle dimensies, Quantum 6, 756 (2022).
https:/​/​doi.org/​10.22331/​q-2022-07-07-756

[58] RH Dicke, Coherentie in spontane stralingsprocessen, Phys. 93, 99 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99

[59] V. Karimipour en L. Memarzadeh, Equientangled bases in willekeurige afmetingen Phys. Rev.A 73, 012329 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.73.012329

[60] G. Rajchel, A. Gąsiorowski en K. Życzkowski, robuuste Hadamard-matrices, unistochastische stralen in Birkhoff-polytoop en equi-verstrengelde bases in samengestelde ruimtes Math. Comp. Wetenschap 12, 473 (2018).
https: / / doi.org/ 10.1007 / s11786-018-0384-y

[61] J. Czartowski, D. Goyeneche, M. Grassl en K. Życzkowski, Isoentangled onderling onbevooroordeelde bases, symmetrische kwantummetingen en ontwerpen met gemengde toestanden, Phys. Ds. Lett. 124, 090503 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.124.090503

[62] F. Del Santo, J. Czartowski, K. Życzkowski en N. Gisin, Iso-verstrengelde bases en gewrichtsmetingen, voordruk arXiv: 2307.06998 (2023).
https:/​/​doi.org/​10.48550/​arXiv.2307.06998
arXiv: 2307.06998

[63] R. Penrose, On Bell non-lokaliteit zonder waarschijnlijkheden: een merkwaardige geometrie, Quantum Reflections (2000).

[64] J. Zimba en R. Penrose, On Bell-non-lokaliteit zonder waarschijnlijkheden: meer merkwaardige geometrie, Stud. Geschiedenis Fil. Wetenschap 24, 697 (1993).
https:/​/​doi.org/​10.1016/​0039-3681(93)90061-N

[65] JE Massad, en PK Aravind, The Penrose dodecahedron revisited, Am. J. Physics 67, 631 (1999).
https: / / doi.org/ 10.1119 / 1.19336

[66] K. Husimi, Enkele formele eigenschappen van de dichtheidsmatrix, Proc. Fys. Wiskunde. Soc. 22, 264 (1940).
https: / / doi.org/ 10.11429 / ppmsj1919.22.4_264

[67] W. Słomczyński en K. Życzkowski, De gemiddelde dynamische entropie van kwantumkaarten op de bol divergeert in de semiklassieke limiet, Phys. Ds. Lett. 80, 1880 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.1880

[68] M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, Perfecte kwantumgradenbogen, voordruk arXiv: 2310.13045 (2023).
https:/​/​doi.org/​10.48550/​arXiv.2310.13045
arXiv: 2310.13045

[69] NCN Maestro 7 2015/​18/​A/​ST2/​00274 website https://​/​chaos.if.uj.edu.pl/​ karol/​Maestro7/​files/​data3/​Numerical_Results.dat.
https://​/​chaos.if.uj.edu.pl/​~karol/​Maestro7/​files/​data3/​Numerical_Results.dat

[70] D. Weingarten, Asymptotisch gedrag van groepsintegralen in de limiet van oneindige rang, J. Math. Fys. 19, 999 (1978).
https: / / doi.org/ 10.1063 / 1.523807

[71] B. Collins en P. Śniady, Integratie met betrekking tot de Haar-maatstaf voor unitaire, orthogonale en symplectische groepen, Commun. Wiskunde. Fys. 264, 773 (2006).
https:/​/​doi.org/​10.1007/​s00220-006-1554-3

[72] G. Rajchel, Quantum mappings en ontwerpen, PhD Thesis, preprint arXiv:2204.13008 (2022).
https:/​/​doi.org/​10.48550/​arXiv.2204.13008
arXiv: 2204.13008

[73] D. Martin en EP Wigner, Groepentheorie en de toepassing ervan op de kwantummechanica van atomaire spectra, Academic Press Inc. NY (1959).
https:/​/​doi.org/​10.1016/​b978-0-12-750550-3.x5001-0

Geciteerd door

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny en Kamil Korzekwa, “Perfecte kwantumgradenbogen”, arXiv: 2310.13045, (2023).

[2] Aaron Z. Goldberg, "Correlaties voor subsets van deeltjes in symmetrische toestanden: wat fotonen doen binnen een lichtstraal als de rest wordt genegeerd", arXiv: 2401.05484, (2024).

Bovenstaande citaten zijn afkomstig van SAO / NASA ADS (laatst bijgewerkt met succes 2024-01-25 11:53:23). De lijst is mogelijk onvolledig omdat niet alle uitgevers geschikte en volledige citatiegegevens verstrekken.

Kon niet ophalen Door Crossref geciteerde gegevens tijdens laatste poging 2024-01-25 11:53:22: kon niet geciteerde gegevens voor 10.22331 / q-2024-01-25-1234 niet ophalen van Crossref. Dit is normaal als de DOI recent is geregistreerd.

Dit artikel is gepubliceerd in Quantum onder de Creative Commons Naamsvermelding 4.0 Internationaal (CC BY 4.0) licentie. Het auteursrecht blijft berusten bij de oorspronkelijke houders van auteursrechten, zoals de auteurs of hun instellingen.

Tijdstempel:

Meer van Quantum Journaal