분리 가능한 상태에 대한 최적화를 기반으로 한 Quantum Wasserstein 거리

분리 가능한 상태에 대한 최적화를 기반으로 한 Quantum Wasserstein 거리

타임 스탬프 : 16 년 2023 월 10 일 오전 35:XNUMX
소스 노드 : 2938953

게자 토스1,2,3,4,5 그리고 요제프 피트릭5,6,7

1이론물리학, University of the Basque Country UPV/EHU, ES-48080 스페인 빌바오
2EHU 양자 센터, 바스크 지방 대학교 UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscay, 스페인
3Donostia International Physics Center(DIPC), ES-20080 산세바스티안, 스페인
4IKERBASQUE, 바스크 과학 재단, ES-48011 빌바오, 스페인
5고체 물리학 및 광학 연구소, Wigner 물리학 연구 센터, HU-1525 부다페스트, 헝가리
6Alfréd Rényi 수학 연구소, Reáltanoda u. 13-15., HU-1053 부다페스트, 헝가리
7Müegyetem rkp의 부다페스트 기술경제대학교 수학연구소 분석 및 운영 연구부. 3., HU-1111 부다페스트, 헝가리

이 논문이 흥미 롭거나 토론하고 싶습니까? SciRate에 댓글을 달거나 댓글 남기기.

추상

우리는 결합의 최적화가 일반적으로 이분 양자 상태가 아닌 이분 분리 가능 상태에서 수행되도록 양자 Wasserstein 거리를 정의하고 그 특성을 조사합니다. 놀랍게도 우리는 자기거리가 양자 피셔 정보와 관련이 있다는 것을 발견했습니다. 우리는 최적의 이분 분리 가능 상태에 해당하는 전송 맵을 제시합니다. 우리는 도입된 양자 Wasserstein 거리가 양자 얽힘을 감지하는 기준과 어떻게 연결되는지 논의합니다. 우리는 양자 상태에 대한 최소화를 최대화로 대체하여 양자 Wasserstein 거리에서 얻을 수 있는 유사 유사 수량을 정의합니다. 우리는 결과를 일반화된 양자 피셔 정보량 계열로 확장합니다.

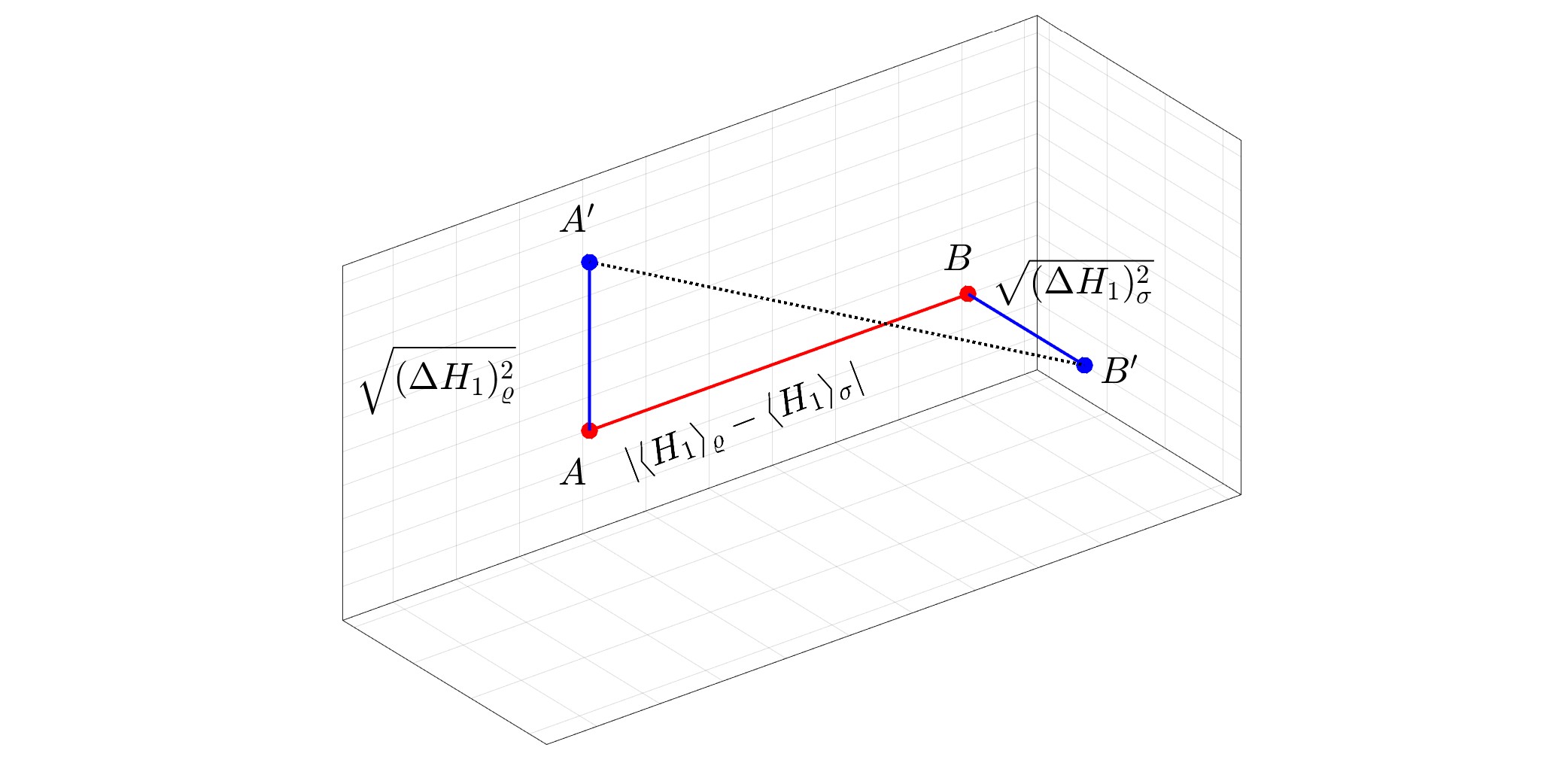
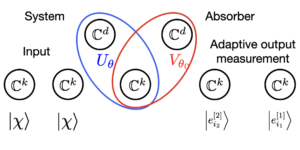
주요 이미지: $N=1.$에 대한 순수 상태 $varrho$와 혼합 상태 $sigma$ 사이의 양자 Wasserstein 거리의 기하학적 표현. 양자 Wasserstein 거리는 $A'$ 사이의 일반적인 유클리드 거리의 $1/sqrt2$ 배와 같습니다. 그리고 $B'.$

인기 요약

일상 생활에서 두 도시의 거리는 한 도시에서 다른 도시로 운전해야 하는 거리가 몇 킬로미터인지 알려줍니다. 여행 중 연료 소비를 측정하여 한 도시에서 다른 도시로 얼마나 쉽게 이동할 수 있는지 특성화하는 것도 가능합니다. 후자가 도로 지형과 관련된 여행 비용을 반영한다는 점, 즉 기본 측정항목에 민감하다는 점에서 더 많은 정보를 제공합니다. 다음으로, 모래 더미를 한 곳에서 다른 곳으로 옮겨야 하는데 새 더미의 형태가 다를 수 있다고 상상해 보겠습니다. 이 경우에도 모래를 옮기는 노력을 운송 비용으로 특성화할 수 있습니다.

거리는 수학, 물리학, 공학에서 중심적인 역할을 합니다. 확률과 통계의 근본적인 문제는 두 확률 분포 사이의 거리에 대한 유용한 측정 방법을 찾는 것입니다. 불행하게도 p(x)와 q(x)와 같이 확률 분포 사이의 거리에 대한 많은 개념은 서로 겹치지 않는 경우 최대가 됩니다. 즉, 다른 하나가 10이 아닐 때 하나는 항상 100입니다. 이는 많은 응용 프로그램에서는 실용적이지 않습니다. 예를 들어, 모래 비유로 돌아가면, 겹치지 않는 두 개의 모래 더미는 거리가 XNUMXkm이든 XNUMXkm이든 상관없이 서로 똑같이 멀리 떨어져 있는 것처럼 보입니다. 최적 전송 이론은 소위 Wasserstein 거리라고 불리는 확률 분포 간의 거리에 대한 대체 개념을 구성하는 방법입니다. 분포가 서로 겹치지 않더라도 최대값이 아닐 수 있고 기본 측정항목(즉, 전송 비용)에 민감하며 본질적으로 하나를 다른 것으로 이동하는 데 필요한 노력을 표현합니다. 마치 모래 언덕인 것처럼.

최근에는 고전적인 Wasserstein 거리를 일반화하여 양자 Wasserstein 거리가 정의되었습니다. 이는 이분 양자 시스템의 양자 상태에 대한 비용 함수의 최소화를 기반으로 합니다. 그것은 양자 세계에서 위에서 언급한 것과 유사한 속성을 가지고 있습니다. 이는 직교 상태에 대해 최대값이 아닐 수 있으며, 이는 예를 들어 알고리즘에 양자 데이터를 가르쳐야 할 때 유용합니다.

우리가 예상할 수 있듯이, 양자 Wasserstein 거리는 고전적인 거리와 매우 다른 특성을 가지고 있습니다. 예를 들어, 양자 상태 자체로부터의 거리를 측정하면 1963이 아닐 수 있습니다. 이것은 이미 수수께끼이지만, 자기 거리는 양자 물리학과 MM 야나세의 기초에 중요한 공헌을 한 노벨상 수상자 EP 위그너(EP Wigner)가 XNUMX년에 소개한 위그너-야나세 왜곡 정보와 관련이 있다는 사실도 밝혀졌습니다.

우리 논문에서 우리는 이 신비한 발견을 또 다른 방향에서 살펴봅니다. 위에서 언급한 최소화를 소위 분리 가능한 상태로 제한합니다. 이는 얽힘을 포함하지 않는 양자 상태입니다. 우리는 자기 거리가 양자 계측학 및 양자 추정 이론의 중심이 되는 양자 피셔 정보가 되고, 예를 들어 유명한 Cramer-Rao 경계에 나타나는 것을 발견했습니다. 이러한 Wasserstein 거리의 특성을 조사함으로써 우리 연구는 양자 Wasserstein 거리 이론을 양자 얽힘 이론과 연결하는 길을 열었습니다.

► BibTeX 데이터

► 참고 문헌

[1] G.몽지. “Mémoire sur la théory des déblais et des remblais”. Mémoires de l'Académie Royale de Sciences de Paris(1781).

[2] L. 칸토로비치. “대중의 이동에 관하여”. 경영 과학 5, 1–4 (1958). URL: http://​/​www.jstor.org/​stable/​2626967.
http : / //www.jstor.org/stable/ 2626967

[3] 에마뉘엘 보아사르, 티보 르 구익, 장 미셸 루브스. "Wasserstein 측정항목을 사용한 배포 템플릿 추정". Bernoulli 21, 740–759(2015).
https://​/​doi.org/​10.3150/​13-bej585

[4] 올렉 부트코프스키. "Wasserstein 측정법에서 Markov 프로세스의 하위 기하학적 수렴 속도". 앤. 신청 확률. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[5] M. 헤어러, J.-C. Mattingly와 M. Scheutzow. “확률적 지연 방정식에 적용되는 점근적 결합 및 해리스 정리의 일반 형태”. 확률. 이론 관계. 필드 149, 223–259(2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[6] M. 헤어러(M. Hairer)와 JC 매팅리(JC Mattingly). "Wasserstein 거리의 스펙트럼 간격과 2D 확률론적 Navier-Stokes 방정식". 앤. 확률. 36, 2050~2091(2008).
https:// / doi.org/ 10.1214/ 08-AOP392

[7] A. Figalli, F. Maggi 및 A. Pratelli. “양적 등가적 불평등에 대한 대중교통 접근 방식”. 꾸미다. 수학. 182, 167-211. (2010).
https : / /doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli와 F. Maggi. “소질량 체제에서 액체 방울과 결정의 형태에 대하여”. 아치. 정액. 기계화. 항문. 201, 143–207 (2011).
https : / /doi.org/ 10.1007 / s00205-010-0383-x

[9] J. 로트(J. Lott)와 C. 빌라니(C. Villani). "최적의 운송을 통한 미터법 공간의 리치 곡률". 앤. 수학. 169(3), 903-991(2009).
https:/ / doi.org/ 10.48550/ arXiv.math/ 0412127

[10] 맥스-K. 폰 레네세와 칼 테오도르 슈트름. "수송 불평등, 기울기 추정, 엔트로피 및 리치 곡률". 통신 순수 응용 프로그램. 수학. 58, 923-940(2005).
https : / / doi.org/ 10.1002 / cpa.20060

[11] 칼 테오도르 슈투름. “미터법 공간의 기하학에 대하여 I”. 액타 수학. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[12] 칼 테오도르 슈투름. “미터법 공간의 기하학 II”. 액타 수학. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[13] Benoı̂t Kloeckner. “Wasserstein 공간에 대한 기하학적 연구: 유클리드 공간”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https : / /doi.org/ 10.2422 / 2036-2145.2010.2.03

[14] 죄르지 팔 게헤르, 타마스 티트코스, 다니엘 비로스텍. “Wasserstein 공간의 아이소메트릭 임베딩 – 개별 사례”. J. 수학. 항문. 신청 480, 123435(2019).
https://doi.org/10.1016/j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. "Wasserstein 공간의 등각 투영 연구 - 실제 선". 트랜스. 아메르. 수학. Soc. 373, 5855-5883(2020).
https:/​/​doi.org/​10.1090/​tran/​8113

[16] 죄르지 팔 게헤르, 타마스 티트코스, 다니엘 비로스텍. “Wasserstein 공간의 등거리 변환 그룹: Hilbertian 사례”. J. 론드. 수학. Soc. 106, 3865-3894(2022).
https://​/​doi.org/​10.1112/​jlms.12676

[17] 죄르지 팔 게헤르, 타마스 티트코스, 다니엘 비로스텍. "Wasserstein 토리 및 구의 등각 강성". Mathematika 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[18] 게르게이 키스(Gergely Kiss)와 타마스 티트코스(Tamás Titkos). "Wasserstein 공간의 등각 강성: 그래프 미터법 사례". 진행 오전. 수학. Soc. 150, 4083–4097(2022).
https : / / doi.org/ 10.1090 / proc / 15977

[19] 죄르지 팔 게헤르, 타마스 티트코스, 다니엘 비로스텍. "실선 위의 이차 워서스타인 공간의 이국적인 등거리 흐름에 대하여". 선형대수학 응용프로그램. (2023).
https : / /doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, SR Park 및 GK Rohde. “라돈 누적 분포 변환 및 이미지 분류에의 적용”. IEEE 트랜스. 이미지 프로세스. 25, 920–934(2016).
https:// / doi.org/ 10.1109/ TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek 및 GK Rohde. “이미지 세트의 변화를 정량화하고 시각화하기 위한 선형 최적 운송 프레임워크”. 국제 J. 컴퓨팅. 비스. 101, 254–269 (2013).
https : / /doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. “최적의 대중교통: 신호 처리 및 기계 학습 애플리케이션”. IEEE 신호 처리 매거진 34, 43–59(2017).
https:// / doi.org/ 10.1109/ MSP.2017.2695801

[23] A. Gramfort, G. Peyré 및 M. Cuturi. “신경영상 데이터의 빠른 최적 전송 평균화”. 의료 영상의 정보 처리. IPMI 2015. 컴퓨터 과학 강의 노트 9123, 261–272(2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu 및 X. Gu. “뇌 형태계측 분석을 위한 Wasserstein 거리를 이용한 형태 분류”. 의료 영상의 정보 처리. IPMI 2015. 컴퓨터 과학 강의 노트 24, 411–423(2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[25] 마틴 아르조프스키(Martin Arjovsky), 수미스 친탈라(Soumith Chintala), 레온 보투(Léon Bottou). “Wasserstein 생성적 적대 네트워크”. In Doina Precup과 Yee Whye Teh, 편집자, 기계 학습에 관한 제34차 국제 회의 논문집. 기계 학습 연구 논문집 70권, 214~223페이지. PMLR(2017). arXiv:1701.07875.
arXiv : 1701.07875

[26] TA El Moselhy 및 YM Marzouk. “최적 지도를 이용한 베이지안 추론”. J. 컴퓨팅. 물리. 231, 7815-7850(2012).
https : / / doi.org/ 10.1016 / j.jcp.2012.07.022

[27] 가브리엘 페이레와 마르코 쿠투리. “계산 최적 전송: 데이터 과학에 적용”. 설립하다. 트렌드 머신 러닝. 11, 355–602(2019).
https : / /doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya 및 Tomaso A Poggio. "와서스타인 손실을 통한 학습". C. Cortes, N. Lawrence, D. Lee, M. Sugiyama 및 R. Garnett의 편집자는 신경 정보 처리 시스템의 발전입니다. 28권. Curran Associates, Inc.(2015). arXiv:1506.05439.
arXiv : 1506.05439

[29] A. Ramdas, NG Trillos 및 M. Cuturi. "Wasserstein 19-표본 검정 및 비모수 검정의 관련 계열". 엔트로피 47, 2017. (XNUMX).
https : / /doi.org/10.3390/e19020047

[30] S. Srivastava, C. Li 및 DB Dunson. "Wasserstein Space의 Barycenter를 통한 확장 가능한 베이즈". J. 마하. 배우다. 결의안. 19, 1–35(2018). arXiv:1508.05880.
arXiv : 1508.05880

[31] 카롤 지치코프스키(Karol Życzkowski)와 보예치에흐 슬롬친스키(Wojeciech Slomczynski). “양자 상태 사이의 몽게 거리”. J. Phys. 답: 수학. Gen. 31, 9095–9104(1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[32] 카롤 지치코프스키(Karol Życzkowski)와 보이치에흐 슬롬친스키(Wojciech Slomczynski). “양자 상태의 구와 기하학에 대한 몽주 측정법”. J. Phys. 답: 수학. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[33] Ingemar Bengtsson과 Karol Życzkowski. "양자 상태의 기하학: 양자 얽힘 소개". 케임브리지 대학 출판부. (2006).
https : / /doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane 및 D. Voiculescu. “추적 상태 공간에 대한 Wasserstein 메트릭의 자유 확률 유사체”. GAFA, 검. 기능 항문. 11, 1125-1138(2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[35] 에릭 A. 칼렌(Eric A. Carlen)과 얀 마스(Jan Maas). “Fermionic Fokker-Planck 방정식이 엔트로피에 대한 기울기 흐름인 비교환 확률의 2-Wasserstein 미터법과 유사합니다.” 커뮤니케이터 수학. 물리. 331, 887-926(2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[36] 에릭 A. 칼렌(Eric A. Carlen)과 얀 마스(Jan Maas). "상세한 균형을 갖춘 양자 마르코프 반군의 기울기 흐름 및 엔트로피 불평등". J. 기능. 항문. 273, 1810~1869(2017).
https : / / doi.org/ 10.1016 / j.jfa.2017.05.003

[37] 에릭 A. 칼렌(Eric A. Carlen)과 얀 마스(Jan Maas). “소산 양자 시스템의 비가환 미적분학, 최적의 수송 및 기능적 불평등”. J. 통계. 물리. 178, 319–378(2020).
https : / /doi.org/ 10.1007 / s10955-019-02434-w

[38] 닐란자나 다타(Nilanjana Datta)와 캄비즈 루제(Cambyse Rouzé). “양자 기능 및 운송 비용 불평등으로 인한 양자 상태의 집중”. J. 수학. 물리. 60, 012202(2019).
https : / /doi.org/ 10.1063 / 1.5023210

[39] 닐란자나 다타(Nilanjana Datta)와 캄비즈 루제(Cambyse Rouzé). "상대 엔트로피, 최적 수송 및 피셔 정보 관련: 양자 HWI 불평등". 앤. 앙리 푸앵카레 21, 2115-2150(2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[40] 프랑수아 골스(François Golse), 클레망 무오(Clément Mouhot), 티에리 폴(Thierry Paul). “양자역학의 평균장과 고전적 한계에 대하여”. 커뮤니케이터 수학. 물리. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[41] 프랑수아 골스(François Golse)와 티에리 폴(Thierry Paul). “평균장 및 준고전적 체제의 슈뢰딩거 방정식”. 아치. 정액. 기계화. 항문. 223, 57–94 (2017).
https : / /doi.org/ 10.1007 / s00205-016-1031-x

[42] 프랑수아 골스(François Golse)와 티에리 폴(Thierry Paul). “양자역학에서의 파동 패킷과 356차 Monge-Kantorovich 거리”. Rendus Math를 비교합니다. 177, 197–2018(XNUMX).
https://doi.org/10.1016/j.crma.2017.12.007

[43] 프랑수아 골스. “평균장 및 준고전적 체제에서의 양자 $N$-체 문제”. 필. 트랜스. R. Soc. A 376, 20170229(2018).
https : / /doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse 및 T. Paul. “양자 최적 운송이 더 저렴합니다.” J. 통계. 물리. 181, 149–162(2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[45] 에마누엘레 칼리오티, 프랑수아 골스, 티에리 폴. “양자 밀도를 위한 최적의 수송을 향하여”. arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv : 2101.03256

[46] 자코모 데 팔마와 다리오 트레비산. “양자 채널을 통한 양자 최적 전송”. 앤. 앙리 푸앵카레 22, 3199-3234(2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[47] 자코모 데 팔마, 밀라드 마비안, 다리오 트레비산, 세스 로이드. “1차 양자 Wasserstein 거리”. IEEE 트랜스. 정보 이론 67, 6627-6643(2021).
https : / //doi.org/10.1109/TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole, Karol Życzkowski. "Quantum Monge-Kantorovich 문제와 밀도 행렬 간의 전송 거리". 물리. Lett 목사. 129, 110402(2022).
https : / /doi.org/10.1103/ PhysRevLett.129.110402

[49] 샘 콜, 미하우 에크슈타인, 슈무엘 프리들랜드, 카롤 지츠코프스키. “양자 최적 운송”. arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv : 2105.06922

[50] R. Bistroń, M. Eckstein 및 K. Życzkowski. “양자 2-Wasserstein 거리의 단조성”. J. Phys. 답: 수학. 이론. 56, 095301(2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos, Dániel Virosztek. “큐비트 상태 공간의 양자 Wasserstein 아이소메트리”. J. 수학. 항문. 신청 522, 126955(2023).
https://doi.org/10.1016/j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe 및 Seth Lloyd. “양자 회로의 Wasserstein 복잡성”. arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu 및 Seth Lloyd. “양자 지구 이동자의 거리로 양자 데이터 학습”. 양자 과학. 기술. 7, 045002(2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[54] EP 위그너와 M. 야나세 무츠오. “배포 정보 내용”. 진행 Natl. Acad. 과학. 미국 49, 910-918(1963).
https : / /doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki 및 Karol Horodecki. "양자 얽힘". 목사님 물리. 81, 865–942 (2009).
https : / /doi.org/10.1103/ RevModPhys.81.865

[56] Otfried Gühne과 Géza Tóth. "얽힘 감지". 물리학 474, 1–75(2009).
https : / //doi.org/ 10.1016 / j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik 및 Marcus Huber. “이론에서 실험까지 얽힘 인증”. Nat. 목사 Phys. 1, 72–87(2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[58] 비토리오 지오반네티, 세스 로이드, 로렌조 맥코네. “양자 강화 측정: 표준 양자 한계 극복”. 과학 306, 1330-1336(2004).
https : / /doi.org/10.1126/ science.1104149

[59] 마테오 조지아 파리. “양자 기술을 위한 양자 추정”. 국제 J. 퀀트. 정보 07, 125–137 (2009).
https : / /doi.org/ 10.1142 / S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna, Jan Kolodynski. “60장 – 광학 간섭계의 양자 한계”. 음식물. 광학 345, 435 – 2015 (1405.7703). arXiv:XNUMX.
https : / /doi.org/ 10.1016 / bs.po.2015.02.003
arXiv : 1405.7703

[61] 루카 페체와 아우구스토 스메르지. “위상 추정의 양자 이론”. GM Tino 및 MA Kasevich, 편집자, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Course 188, Varenna). 691~741페이지. IOS 출판사, 암스테르담(2014). arXiv:1411.5164.
arXiv : 1411.5164

[62] Géza Tóth와 Dénes Petz. “분산의 극한 특성과 양자 피셔 정보”. 물리. A 87, 032324(2013).
https : / /doi.org/10.1103/ PhysRevA.87.032324

[63] 식시아 유. “볼록한 분산 지붕으로서의 양자 피셔 정보”. arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv : 1302.5311

[64] 게자 토스(Géza Tóth)와 플로리안 프뢰비스(Florian Fröwis). "밀도 행렬의 볼록 분해를 기반으로 한 분산 및 양자 피셔 정보와의 불확실성 관계". 물리. 연구 4, 013075(2022).
https : / /doi.org/10.1103/ PhysRevResearch.4.013075

[65] 샤오헨 치우(Shao-Hen Chiew)와 마누엘 게스너(Manuel Gessner). “양자 피셔 정보와의 총 불확실성 관계 개선”. 물리. 연구 4, 013076(2022).
https : / /doi.org/10.1103/ PhysRevResearch.4.013076

[66] CW 헬스트롬. “양자 검출 및 추정 이론”. 학술 출판사, 뉴욕. (1976). URL: www.elsevier.com/books/퀀텀-검출-and-estimation-theory/helstrom/978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[67] AS 홀레보. “양자 이론의 확률론적, 통계적 측면”. 북부 네덜란드, 암스테르담. (1982).

[68] 사무엘 L. 브라운슈타인과 칼튼 M. 동굴. "통계적 거리와 양자 상태의 기하학". 물리학 레트 목사 72, 3439–3443(1994).
https : / /doi.org/10.1103/ PhysRevLett.72.3439

[69] 사무엘 L 브라운스타인, 칼튼 M 케이브스, 제라드 J 밀번. "일반화된 불확실성 관계: 이론, 예 및 로렌츠 불변성". 앤. 물리. 247, 135-173(1996).
https : / /doi.org/ 10.1006 / aphy.1996.0040

[70] 데네스 페츠. “양자정보이론과 양자통계”. 스프링거, 베를린, 하이더베르크. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[71] 게자 토스와 이아고바 아펠라니즈. "양자 정보 과학 관점에서 본 양자 계측". J. Phys. 답: 수학. 이론. 47, 424006(2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied, Philipp Treutlein. "원자 앙상블의 비고전적 상태를 사용한 양자 계측". 목사 모드. 물리학 90, 035005 (2018).
https : / /doi.org/10.1103/ RevModPhys.90.035005

[73] 마르코 바르비에리. “광학 양자 계측”. PRX 퀀텀 3, 010202(2022).
https : / / doi.org/ 10.1103 / PRXQuantum.3.010202

[74] 졸탄 레카(Zoltán Léka)와 데네스 페츠(Dénes Petz). “행렬 분산의 일부 분해”. 확률. 수학. 통계학자. 33, 191–199(2013). arXiv:1408.2707.
arXiv : 1408.2707

[75] 데네스 페츠(Dénes Petz)와 다니엘 비로스텍(Dániel Virosztek). “행렬 분산에 대한 특성화 정리”. Acta Sci. 수학. (Szeged) 80, 681–687 (2014).
https:/​/​doi.org/​10.14232/​actasm-013-789-z

[76] 후지와라 아키오와 이마이 히로시. “다양한 양자 채널을 통한 섬유 다발과 양자 통계에의 적용”. J. Phys. 답: 수학. 이론. 41, 255304(2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[77] BM Escher, RL de Matos Filho 및 L. Davidovich. "시끄러운 양자 강화 계측의 궁극적인 정밀도 한계를 추정하기 위한 일반적인 프레임워크". Nat. 물리. 7, 406-411(2011).
https : / /doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński, Mădălin Guţă. “양자 강화 계측에서 파악하기 어려운 하이젠베르크 한계”. Nat. 커뮤니케이터 3, 1063(2012).
https : / /doi.org/ 10.1038 / ncomms2067

[79] 이만 마비안. “양자 열역학에서 양자 피셔 정보의 조작적 해석”. 물리. Lett 목사. 129, 190502(2022).
https : / /doi.org/10.1103/ PhysRevLett.129.190502

[80] 라인하르트 F. 베르너. "숨겨진 변수 모델을 인정하는 Einstein-Podolsky-Rosen 상관 관계가 있는 양자 상태". 물리. A 40, 4277-4281(1989).
https : / /doi.org/10.1103/ PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss 및 M. Lewenstein. “구별할 수 없는 입자 시스템의 양자 상관관계”. 앤. 물리. 299, 88–127 (2002).
https : / /doi.org/ 10.1006 / aphy.2002.6268

[82] 이치카와 츠바사, 사사키 도시히코, 츠츠이 이즈미, 요네자와 노부히로. “대칭 교환과 다중 얽힘”. 물리. A 78, 052105(2008).
https : / /doi.org/10.1103/ PhysRevA.78.052105

[83] 파웰 호로데츠키. "분리성 기준 및 양의 부분 전치가 있는 분리 불가능한 혼합 상태". 물리. 레트 사람. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[84] 애셔 페레스. "밀도 매트릭스에 대한 분리 가능성 기준". 물리학 레트 목사 77, 1413–1415(1996).
https : / /doi.org/10.1103/ PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki, Ryszard Horodecki. "바운드 얽힘이 활성화될 수 있습니다." 물리. Lett 목사. 82, 1056-1059(1999).
https : / /doi.org/10.1103/ PhysRevLett.82.1056

[86] Géza Tóth와 Tamás Vértesi. "양의 부분 전치를 갖는 양자 상태는 계측에 유용합니다." 물리. Lett 목사. 120, 020506(2018).
https : / /doi.org/10.1103/ PhysRevLett.120.020506

[87] 스콧 힐과 윌리엄 K. 우터스. “양자 비트 쌍의 얽힘”. 물리. Lett 목사. 78, 5022-5025(1997).
https : / /doi.org/10.1103/ PhysRevLett.78.5022

[88] 윌리엄 K. 우터스. "두 큐비트의 임의 상태 형성의 얽힘". 물리. Lett 목사. 80, 2245-2248(1998).
https : / /doi.org/10.1103/ PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal 및 Armin Uhlmann. “지원의 얽힘”. 퀀트-ph/​9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv : 퀀트 -PH / 9803033

[90] 존 A. 스몰린(John A. Smolin), 프랭크 베르스트라에트(Frank Verstraete), 안드레아스 윈터(Andreas Winter). “지원의 얽힘과 다자적 국가 증류”. 물리. A 72, 052317(2005).
https : / /doi.org/10.1103/ PhysRevA.72.052317

[91] 홀거 F. 호프만(Holger F. Hofmann)과 다케우치 시게키(Shegeki Takeuchi). "얽힘의 서명으로서 지역적 불확실성 관계의 위반". 물리. A 68, 032103(2003).
https : / /doi.org/10.1103/ PhysRevA.68.032103

[92] 오트프리트 구네. “불확실성 관계를 통한 얽힘의 특성화”. 물리. Lett 목사. 92, 117903(2004).
https : / /doi.org/10.1103/ PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth 및 Peter Adam. "국소적인 불확실성 관계에 기초한 얽힘 기준은 계산 가능한 교차 규범 기준보다 엄격하게 강력합니다." 물리. A 74, 010301(2006).
https : / /doi.org/10.1103/ PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza, Géza Tóth. "임의의 스핀에 대한 스핀 압착 불평등". 물리학 레트 목사 107, 240502(2011).
https : / /doi.org/10.1103/ PhysRevLett.107.240502

[95] AR 에드먼즈. “양자역학의 각운동량”. 프린스턴 대학 출판부. (1957).
https : / /doi.org/ 10.1515 / 9781400884186

[96] 게자 토스. "집합 측정을 통한 보소닉 원자의 광학 격자에서의 얽힘 감지". 물리학 A 69, 052327(2004).
https : / /doi.org/10.1103/ PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne, Hans J. Briegel. "최적의 스핀 압착 부등식은 스핀 모델에서 바운드 얽힘을 감지합니다." 물리학 레트 목사 99, 250405 (2007).
https : / /doi.org/10.1103/ PhysRevLett.99.250405

[98] 게자 토스(Géza Tóth)와 모건 W 미첼(Morgan W Mitchell). “원자 앙상블에서 거시적 단일항 상태의 생성”. 새로운 J. Phys. 12, 053007(2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[99] 게자 토스. "대칭 Dicke 상태 근처에서 다중 부분 얽힘 감지". J. 옵션. Soc. 오전. B 24, 275–282 (2007).
https : / /doi.org/ 10.1364 / JOSAB.24.000275

[100] 게자 토스(Géza Tóth), 토비아스 모로더(Tobias Moroder), 오트프리트 구네(Otfried Gühne). "볼록한 지붕 얽힘 조치 평가". 물리. Lett 목사. 114, 160501(2015).
https : / /doi.org/10.1103/ PhysRevLett.114.160501

[101] 리벤 반덴베르게(Lieven Vandenberghe)와 스티븐 보이드(Stephen Boyd). “반한정 프로그래밍”. SIAM 리뷰 38, 49–95(1996).
https : / /doi.org/ 10.1137 / 1038003

[102] 게자 토스. "다중 얽힘 및 고정밀 계측". 물리학 A 85, 022322(2012).
https : / /doi.org/10.1103/ PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé, Augusto Smerzi. "피셔 정보 및 다중 입자 얽힘". 물리학 A 85, 022321(2012).
https : / /doi.org/10.1103/ PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki, Ryszard Horodecki. "숨겨진 도량형 유용성 활성화". 물리. Lett 목사. 125, 020402(2020).
https : / /doi.org/10.1103/ PhysRevLett.125.020402

[105] AC 도허티, 파블로 A. 파릴로, 페데리코 M. 스페달리에리. “분리 가능한 상태와 얽힌 상태의 구별”. 물리. Lett 목사. 88, 187904(2002).
https : / /doi.org/10.1103/ PhysRevLett.88.187904

[106] 앤드류 C. 도허티, 파블로 A. 파릴로, 페데리코 M. 스페달리에리. “분리성 기준의 완전한 계열”. 물리. A 69, 022308(2004).
https : / /doi.org/10.1103/ PhysRevA.69.022308

[107] 앤드류 C. 도허티, 파블로 A. 파릴로, 페데리코 M. 스페달리에리. "다중 얽힘 감지". 물리. A 71, 032333(2005).
https : / /doi.org/10.1103/ PhysRevA.71.032333

[108] 해롤드 올리비에(Harold Ollivier)와 보이치에흐 H. 주렉(Wojciech H. Zurek). “양자 불일치: 상관관계의 양자성의 척도”. 물리. Lett 목사. 88, 017901(2001).
https : / /doi.org/10.1103/ PhysRevLett.88.017901

[109] L. Henderson 및 V. Vedral. “고전적, 양자적, 총 상관관계”. J. Phys. 답: 수학. Gen. 34, 6899(2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De), Ujjwal Sen. “양자 불화와 그 동맹국: 최근 진행 상황에 대한 검토”. 대표 프로그램. 물리. 81, 024001(2017).
https : / /doi.org/ 10.1088 / 1361-6633 / a872f

[111] 데네스 페츠. “양자역학의 공분산과 피셔 정보”. J. Phys. 답: 수학. 35, 929(2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[112] 파올로 기빌리스코, 히아이 후미오, 데네스 페츠. “양자 공분산, 양자 피셔 정보 및 불확실성 관계”. IEEE 트랜스. 정보 이론 55, 439–443 (2009).
https : / //doi.org/10.1109/TIT.2008.2008142

[113] D. 페츠와 C. 기니아. “양자 피셔 정보 소개”. 27권, 261~281페이지. 월드 사이언티픽. (2011).
https : / /dodo.org/ 10.1142 / 9789814338745_0015

[114] 프랭크 한센. "메트릭 조정 편향 정보". 진행 Natl. Acad. 과학. 미국 105, 9909-9916(2008).
https : / /doi.org/ 10.1073 / pnas.0803323105

[115] 파올로 기빌리스코, 다비데 지롤라미, 프랭크 한센. "메트릭 조정 스큐 정보를 통한 로컬 양자 불확실성 및 간섭계 전력에 대한 통합 접근 방식". 엔트로피 23, 263(2021).
https : / /doi.org/10.3390/e23030263

[116] MATLAB. “9.9.0.1524771(r2020b)”. MathWorks Inc. Natick, 매사추세츠(2020).

[117] 모세크 ApS. “MATLAB 매뉴얼용 MOSEK 최적화 툴박스. 버전 9.0”. (2019). URL: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[118] J. Löfberg. “YALMIP: MATLAB의 모델링 및 최적화를 위한 도구 상자”. CACSD 회의 진행 중. 대만 타이베이(2004).

[119] 게자 토스. "QUBIT4MATLAB V3.0: MATLAB용 양자 정보 과학 및 양자 광학용 프로그램 패키지". 계산. 물리. 커뮤니케이터 179, 430–437 (2008).
https : / /doi.org/ 10.1016 / j.cpc.2008.03.007

[120] QUBIT4MATLAB 패키지는 https:/​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433 및 개인 홈 페이지 https:/​/​gtoth.eu/​qubit4matlab.html에서 사용할 수 있습니다.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

인용

[1] Laurent Lafleche, "양자 최적 전송 및 약한 토폴로지", arXiv : 2306.12944, (2023).

위의 인용은 SAO / NASA ADS (마지막으로 성공적으로 업데이트 됨 2023-10-16 14:47:44). 모든 출판사가 적절하고 완전한 인용 데이터를 제공하지는 않기 때문에 목록이 불완전 할 수 있습니다.

가져올 수 없습니다 Crossref 인용 자료 마지막 시도 중 2023-10-16 14:47:42 : Crossref에서 10.22331 / q-2023-10-16-1143에 대한 인용 데이터를 가져올 수 없습니다. DOI가 최근에 등록 된 경우 이는 정상입니다.

이 백서는 Quantum에서 Creative Commons Attribution 4.0 International(CC BY 4.0) 특허. 저작권은 저자 또는 기관과 같은 원래 저작권 보유자에게 있습니다.

타임 스탬프 :

더보기 양자 저널