Distanza quantistica di Wasserstein basata su un'ottimizzazione su stati separabili

Distanza quantistica di Wasserstein basata su un'ottimizzazione su stati separabili

Timestamp: 16 ottobre 2023 10:35
Nodo di origine: 2938953

Géza Tóth1,2,3,4,5 e József Pitrik5,6,7

1Fisica Teorica, Università dei Paesi Baschi UPV/EHU, ES-48080 Bilbao, Spagna
2EHU Quantum Center, Università dei Paesi Baschi UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscaglia, Spagna
3Centro Internazionale di Fisica Donostia (DIPC), ES-20080 San Sebastián, Spagna
4IKERBASQUE, Fondazione basca per la scienza, ES-48011 Bilbao, Spagna
5Istituto di fisica e ottica dello stato solido, Centro di ricerca di fisica Wigner, HU-1525 Budapest, Ungheria
6Istituto di Matematica Alfréd Rényi, Reáltanoda u. 13-15., HU-1053 Budapest, Ungheria
7Dipartimento di Analisi e Ricerca Operativa, Istituto di Matematica, Università di Tecnologia ed Economia di Budapest, Müegyetem rkp. 3., HU-1111 Budapest, Ungheria

Trovi questo documento interessante o vuoi discuterne? Scrivi o lascia un commento su SciRate.

Astratto

Definiamo la distanza quantistica di Wasserstein in modo tale che l'ottimizzazione dell'accoppiamento venga effettuata su stati bipartiti separabili piuttosto che su stati quantistici bipartiti in generale, ed esaminiamo le sue proprietà. Sorprendentemente, scopriamo che l'autodistanza è correlata all'informazione quantistica di Fisher. Presentiamo una mappa di trasporto corrispondente ad uno stato separabile bipartito ottimale. Discutiamo di come la distanza quantistica di Wasserstein introdotta sia collegata ai criteri che rilevano l'entanglement quantistico. Definiamo quantità simili alla varianza che possono essere ottenute dalla distanza quantistica di Wasserstein sostituendo la minimizzazione sugli stati quantistici con una massimizzazione. Estendiamo i nostri risultati a una famiglia di quantità di informazioni quantistiche generalizzate di Fisher.

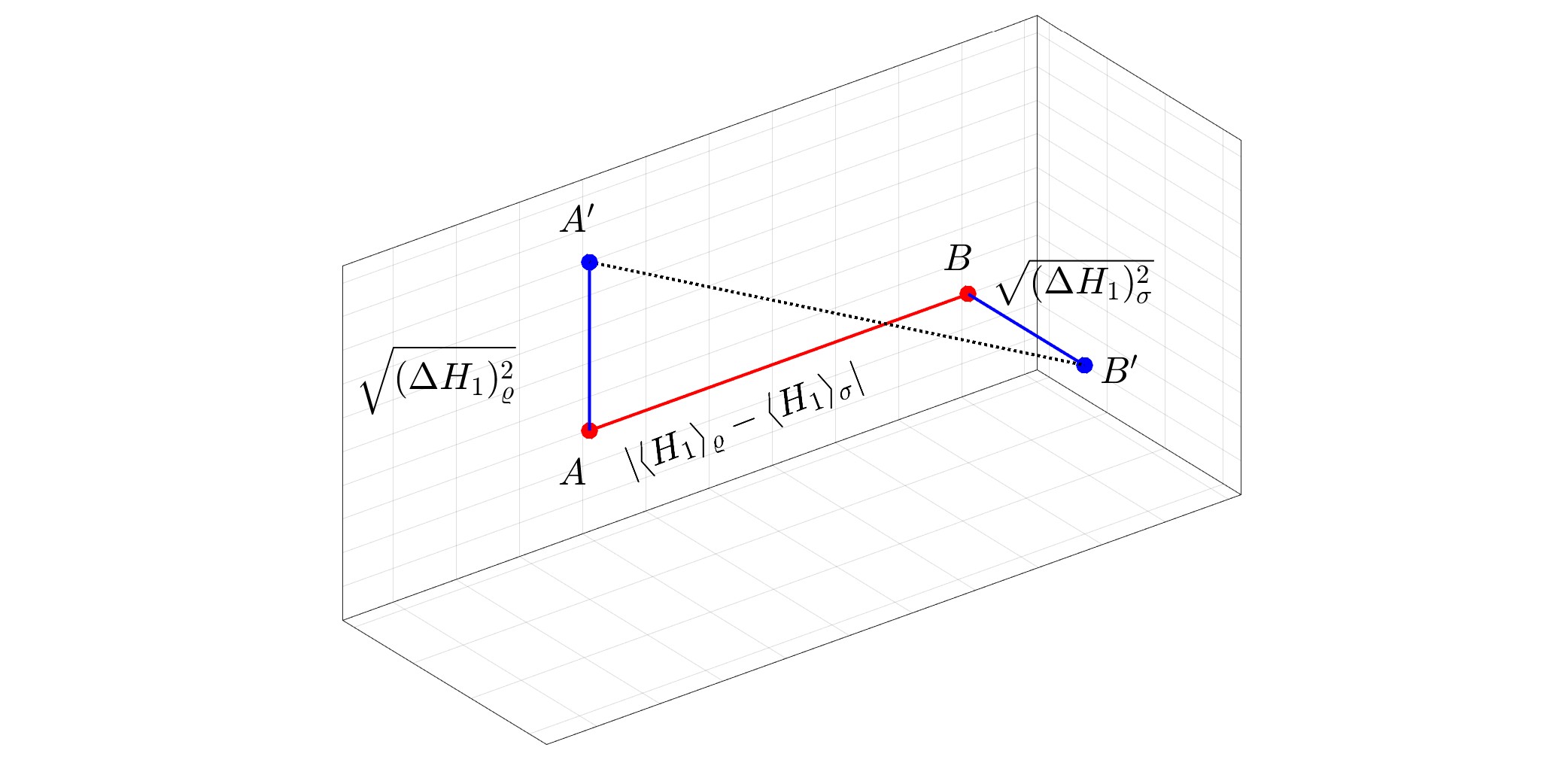
Immagine in primo piano: Rappresentazione geometrica della distanza quantistica di Wasserstein tra uno stato puro $varrho$ e uno stato misto $sigma$ per $N=1.$ La distanza quantistica di Wasserstein è pari a $1/sqrt2$ volte la solita distanza euclidea tra $A'$ e $B'.$

Riepilogo popolare

Nella vita di tutti i giorni, la distanza di due città ci dice quanti chilometri dobbiamo percorrere dall'una all'altra. È anche possibile caratterizzare la facilità con cui possiamo spostarci da una città all'altra misurando il consumo di carburante durante il nostro viaggio. Quest'ultimo è più informativo nel senso che riflette il costo del viaggio legato alla topografia della strada, ad es. e., è sensibile alla metrica sottostante. Successivamente, immaginiamo di dover spostare un mucchio di sabbia da un posto all'altro e il nuovo mucchio potrebbe avere una forma diversa. Anche in questo caso possiamo caratterizzare lo sforzo per spostare la sabbia in base al costo del trasporto.

Le distanze svolgono un ruolo centrale in matematica, fisica e ingegneria. Un problema fondamentale in probabilità e statistica è trovare misure utili della distanza tra due distribuzioni di probabilità. Sfortunatamente, molte nozioni di distanza tra distribuzioni di probabilità, ad esempio p(x) e q(x), sono massimali se non si sovrappongono tra loro, ad es. e., uno è sempre zero quando l'altro è diverso da zero. Questo non è pratico per molte applicazioni. Ad esempio, tornando all'analogia con la sabbia, due mucchi di sabbia non sovrapposti sembrano essere ugualmente distanti l'uno dall'altro, indipendentemente dal fatto che la loro distanza sia di 10 km o 100 km. La teoria del trasporto ottimale è un modo per costruire una nozione alternativa di distanza tra distribuzioni di probabilità, la cosiddetta distanza di Wasserstein. Può essere non massimale anche se le distribuzioni non si sovrappongono tra loro, è sensibile alla metrica sottostante (cioè il costo del trasporto) ed essenzialmente esprime lo sforzo necessario per passare dall'una all'altra, come se fossero colline di sabbia.

Recentemente la distanza quantistica di Wasserstein è stata definita generalizzando la distanza di Wasserstein classica. Si basa sulla minimizzazione di una funzione di costo sugli stati quantistici di un sistema quantistico bipartito. Ha la proprietà analoga a quella menzionata sopra nel mondo quantistico. Può essere non massimale per stati ortogonali, il che è utile, ad esempio, quando dobbiamo insegnare i dati quantistici a un algoritmo.

Come possiamo aspettarci, anche la distanza quantistica di Wasserstein ha proprietà molto diverse da quelle della sua controparte classica. Ad esempio, quando misuriamo la distanza di uno stato quantistico da se stesso, può essere diverso da zero. Anche se questo è già sconcertante, è stato anche scoperto che l’autodistanza è correlata all’informazione di distorsione Wigner-Yanase, introdotta nel 1963 dal premio Nobel E. P. Wigner, che ha dato contributi vitali ai fondamenti della fisica quantistica e a M. M. Yanase.

Nel nostro articolo, esaminiamo questa misteriosa scoperta da un’altra direzione. Limitiamo la minimizzazione sopra menzionata ai cosiddetti stati separabili. Questi sono gli stati quantistici che non contengono entanglement. Scopriamo che l'autodistanza diventa l'informazione quantistica di Fisher, una quantità centrale nella metrologia quantistica e nella teoria della stima quantistica, e che appare ad esempio nel famoso limite di Cramer-Rao. Esaminando le proprietà di tale distanza di Wasserstein, il nostro lavoro apre la strada per collegare la teoria della distanza quantistica di Wasserstein alla teoria dell’entanglement quantistico.

► dati BibTeX

► Riferimenti

, G. Monge. “Mémoire sur la théory des déblais et des remblais”. Memorie dell'Académie Royale de Sciences di Parigi (1781).

, L. Kantorovich. “Sulla traslocazione delle masse”. Scienze gestionali 5, 1–4 (1958). URL: http://​/​www.jstor.org/​stable/​2626967.
http: / / www.jstor.org/ stabile / 2626967

, Emmanuel Boissard, Thibaut Le Gouic e Jean-Michel Loubes. “Stima del modello di distribuzione con metriche Wasserstein”. Bernoulli 21, 740–759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

, Oleg Butkovskij. "Tassi subgeometrici di convergenza dei processi di Markov nella metrica di Wasserstein". Anna. Appl. Probabile 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

, M. Hairer, J.-C. Mattingly e M. Scheutzow. "Accoppiamento asintotico e una forma generale del teorema di Harris con applicazioni alle equazioni di ritardo stocastiche". Probabile Teoria Relaz. Campi 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

, M. Hairer e JC Mattingly. "Lacune spettrali nelle distanze di Wasserstein e nelle equazioni stocastiche di Navier-Stokes 2D". Anna. Probabile 36, 2050–2091 (2008).
https://​/​doi.org/​10.1214/​08-AOP392

, A. Figalli, F. Maggi e A. Pratelli. "Un approccio di trasporto di massa alle disuguaglianze isoperimetriche quantitative". Inventare. Matematica. 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

, A. Figalli e F. Maggi. “Sulla forma di gocce liquide e cristalli nel regime di piccola massa”. Arco. Razione. Mecc. Anale. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

, J. Lott e C. Villani. “Curvatura di Ricci per spazi di misura metrica tramite trasporto ottimo”. Anna. di matematica. 169 (3), 903–991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

, Max-K. von Renesse e Karl-Theodor Sturm. "Disuguaglianza di trasporto, stime del gradiente, entropia e curvatura di Ricci". Com. Appl. puro Matematica. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

, Karl-Theodor Sturm. “Sulla geometria degli spazi di misura metrica I”. Atti Matematici. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

, Karl-Theodor Sturm. “Sulla geometria degli spazi di misura metrici II”. Atti Matematici. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

, Benoıt Kloeckner. “Uno studio geometrico degli spazi di Wasserstein: spazi euclidei”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03

, György Pál Gehér, Tamás Titkos e Dániel Virosztek. "Sugli incastri isometrici degli spazi di Wasserstein - il caso discreto". J. Matematica. Anale. Appl. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

, György Pál Gehér, T. Titkos, Dániel Virosztek. “Studio isometrico degli spazi di Wasserstein – la linea reale”. Trans. Amer. Matematica. Soc. 373, 5855–5883 (2020).
https: / / doi.org/ 10.1090 / tran / 8113

, György Pál Gehér, Tamás Titkos e Dániel Virosztek. “Il gruppo isometrico degli spazi di Wasserstein: il caso Hilbertiano”. J. Lond. Matematica. Soc. 106, 3865–3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

, György Pál Gehér, Tamás Titkos e Dániel Virosztek. "Rigidità isometrica di tori e sfere di Wasserstein". Mathematika 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

, Gergely Kiss e Tamás Titkos. "Rigidità isometrica degli spazi di Wasserstein: il caso grafometrico". Proc. Sono. Matematica. Soc. 150, 4083–4097 (2022).
https://​/​doi.org/​10.1090/​proc/​15977

, György Pál Gehér, Tamás Titkos e Dániel Virosztek. "Sul flusso isometrico esotico dello spazio quadratico di Wasserstein sulla linea reale". Appl. di algebra lineare (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

, S. Kolouri, SR Park e GK Rohde. "La trasformazione della distribuzione cumulativa del Radon e la sua applicazione alla classificazione delle immagini". IEEE Trans. Processo di immagine. 25, 920–934 (2016).
https://​/​doi.org/​10.1109/​TIP.2015.2509419

, W. Wang, D. Slepc̆ev, S. Basu, J. A. Ozolek e G. K. Rohde. "Un quadro di trasporto ottimale lineare per quantificare e visualizzare le variazioni in serie di immagini". interno J. Calcolo. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

, S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, G. K. Rohde. "Trasporto di massa ottimale: elaborazione del segnale e applicazioni di apprendimento automatico". Rivista IEEE sull'elaborazione dei segnali 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

, A. Gramfort, G. Peyré e M. Cuturi. "Media rapida del trasporto ottimale dei dati di neuroimaging". Elaborazione delle informazioni nell'imaging medico. IPMI 2015. Appunti delle lezioni di informatica 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

, Z. Su, W. Zeng, Y. Wang, Z. L. Lu e X. Gu. "Classificazione delle forme utilizzando la distanza di Wasserstein per l'analisi della morfometria del cervello". Elaborazione delle informazioni nell'imaging medico. IPMI 2015. Appunti delle lezioni di informatica 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

, Martin Arjovsky, Soumith Chintala e Léon Bottou. “Reti avversarie generative di Wasserstein”. In Doina Precup e Yee Whye Teh, a cura di, Atti della 34a Conferenza internazionale sull'apprendimento automatico. Volume 70 degli Atti della ricerca sull'apprendimento automatico, pagine 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

, TA El Moselhy e YM Marzouk. "Inferenza bayesiana con mappe ottimali". J. Calcolo. Fis. 231, 7815–7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022

, Gabriel Peyré e Marco Cuturi. "Trasporto ottimale computazionale: con applicazioni alla scienza dei dati". Trovato. Apprendimento automatico delle tendenze. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073 mila

, Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya e Tomaso A Poggio. “Imparare con una perdita di Wasserstein”. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama e R. Garnett, redattori, Advances in Neural Information Processing Systems. Volume 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

, A. Ramdas, N. G. Trillos e M. Cuturi. "Sul test di Wasserstein a due campioni e sulle relative famiglie di test non parametrici". Entropia 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

, S. Srivastava, C. Li e DB Dunson. "Bayes scalabile tramite baricentro nello spazio Wasserstein". J.Mach. Imparare. Ris. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

, Karol Życzkowski e Wojeciech Slomczynski. “La distanza di Monge tra stati quantistici”. J. fisico. R: Matematica. Gen. 31, 9095–9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

, Karol Życzkowski e Wojciech Slomczynski. “La metrica di Monge sulla sfera e la geometria degli stati quantistici”. J. fisico. R: Matematica. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

, Ingemar Bengtsson e Karol Życzkowski. "Geometria degli stati quantistici: un'introduzione all'entanglement quantistico". Pressa dell'Università di Cambridge. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

, P. Biane e D. Voiculescu. "Un analogo probabilistico libero della metrica di Wasserstein sullo spazio delle tracce". GAFA, Geom. Funz. Anale. 11, 1125–1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

, Eric A. Carlen e Jan Maas. "Un analogo della metrica 2-Wasserstein nella probabilità non commutativa in base alla quale l'equazione fermionica di Fokker-Planck è un flusso gradiente per l'entropia". Comune. Matematica. Fis. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

, Eric A. Carlen e Jan Maas. "Flusso di gradiente e disuguaglianze di entropia per semigruppi di Markov quantistici con bilancio dettagliato". J. Funz. Anale. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

, Eric A. Carlen e Jan Maas. “Calcolo non commutativo, trasporto ottimo e disuguaglianze funzionali in sistemi quantistici dissipativi”. J. Stat. Fis. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

, Nilanjana Datta e Cambyse Rouzé. "Concentrazione di stati quantistici da disuguaglianze quantistiche funzionali e di costo di trasporto". J. Matematica. Fis. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210 mila

, Nilanjana Datta e Cambyse Rouzé. "Relazione entropia relativa, trasporto ottimale e informazioni di Fisher: una disuguaglianza HWI quantistica". Anna. Henri Poincaré 21, 2115–2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

, François Golse, Clément Mouhot e Thierry Paul. “Sul campo medio e sui limiti classici della meccanica quantistica”. Comune. Matematica. Fis. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

, François Golse e Thierry Paul. "L'equazione di Schrödinger nel campo medio e nel regime semiclassico". Arco. Razione. Mecc. Anale. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

, François Golse e Thierry Paul. “Pacchetti d'onda e distanza quadratica di Monge-Kantorovich nella meccanica quantistica”. Comptes Rendus Math. 356, 177–197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

, François Golse. “Il problema del corpo quantistico $N$ nel campo medio e nel regime semiclassico”. Fil. Trans. R.Soc. A376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

, E. Caglioti, F. Golse e T. Paul. “Il trasporto quantistico ottimale è più economico”. J. Stat. Fis. 181, 149–162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

, Emanuele Caglioti, François Golse, and Thierry Paul. “Verso il trasporto ottimale per le densità quantistiche”. arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

, Giacomo De Palma e Dario Trevisan. “Trasporto ottimale quantistico con canali quantistici”. Anna. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

, Giacomo De Palma, Milad Marvian, Dario Trevisan e Seth Lloyd. “La distanza quantistica di Wasserstein di ordine 1”. IEEE Trans. Inf. Teoria 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

, Shmuel Friedland, Michał Eckstein, Sam Cole e Karol Życzkowski. “Problema quantistico di Monge-Kantorovich e distanza di trasporto tra matrici di densità”. Fis. Rev. Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

, Sam Cole, Michał Eckstein, Shmuel Friedland e Karol Życzkowski. “Trasporto ottimale quantistico”. arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

, R. Bistroń, M. Eckstein e K. Życzkowski. "Monotonicità di una distanza quantistica 2-Wasserstein". J. fisico. R: Matematica. Teore. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

, György Pál Gehér, József Pitrik, Tamás Titkos e Dániel Virosztek. “Isometrie quantistiche di Wasserstein sullo spazio degli stati dei qubit”. J. Matematica. Anale. Appl. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

, Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe e Seth Lloyd. “Complessità di Wasserstein dei circuiti quantistici”. arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

, Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu e Seth Lloyd. "Apprendimento dei dati quantistici con la distanza del motore quantistico della terra". Sci quantistica. Tecnologia. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

, EP Wigner e Mutsuo M. Yanase. “Contenuti informativi delle distribuzioni”. Proc. Natl. Accade. Sci. USA 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

, Ryszard Horodecki, Paweł Horodecki, Michał Horodecki e Karol Horodecki. "Entanglement quantistico". Rev.mod. Fis. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

, Otfried Gühne e Géza Tóth. "Rilevamento dell'intreccio". Fis. Rep. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

, Nicolai Friis, Giuseppe Vitagliano, Mehul Malik e Marcus Huber. “Certificazione dell’entanglement dalla teoria all’esperimento”. Naz. Rev. Fis. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

, Vittorio Giovannetti, Seth Lloyd, Lorenzo Maccone. "Misurazioni quantistiche avanzate: superamento del limite quantistico standard". Scienza 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

, Matteo G.A. Parigi. “Stima quantistica per la tecnologia quantistica”. interno J.quant. Inf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

, Rafal Demkowicz-Dobrzanski, Marcin Jarzyna e Jan Kolodynski. “Capitolo quattro – Limiti quantistici nell’interferometria ottica”. Progr. Ottiche 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

, Luca Pezze e Augusto Smerzi. “Teoria quantistica della stima delle fasi”. In G.M. Tino e M.A. Kasevich, curatori, Atom Interferometry (Proc. Int. Scuola di Fisica “Enrico Fermi”, Corso 188, Varenna). Pagine 691–741. IOS Press, Amsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

, Géza Tóth e Dénes Petz. “Proprietà estreme della varianza e informazione quantistica di Fisher”. Fis. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

, Sixia Yu. "L'informazione quantistica di Fisher come tetto convesso della varianza". arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

, Géza Tóth e Florian Fröwis. “Rapporti di incertezza con la varianza e l'informazione quantistica di Fisher basata su scomposizioni convesse di matrici di densità”. Fis. Rev. Ricerca 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

, Shao-Hen Chiew e Manuel Gessner. "Migliorare le relazioni di incertezza della somma con l'informazione quantistica di Fisher". Fis. Rev. Ricerca 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

, CW Helstrom. “Teoria della rilevazione e stima quantistica”. Stampa accademica, New York. (1976). url: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

, AS Holevo. “Aspetti probabilistici e statistici della teoria quantistica”. Olanda Settentrionale, Amsterdam. (1982).

, Samuel L. Braunstein e Carlton M. Grotte. "Distanza statistica e geometria degli stati quantistici". Fis. Rev. Lett. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

, Samuel L Braunstein, Carlton M Caves e Gerard J Milburn. "Relazioni di incertezza generalizzate: teoria, esempi e invarianza di Lorentz". Anna. Fis. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

, Dénes Petz. “Teoria dell’informazione quantistica e statistica quantistica”. Springer, Berlino, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

, Géza Tóth e Iagoba Apellaniz. “La metrologia quantistica dal punto di vista della scienza dell’informazione quantistica”. J. fisico. R: Matematica. Teore. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

, Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied e Philipp Treutlein. "Metrologia quantistica con stati non classici di insiemi atomici". Rev.mod. Fis. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

, Marco Barbieri. “Metrologia quantistica ottica”. PRX Quantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

, Zoltán Léka e Dénes Petz. "Alcune scomposizioni delle varianze delle matrici". Probabile Matematica. Statista. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

, Dénes Petz e Dániel Virosztek. "Un teorema di caratterizzazione per varianze di matrici". Acta Sci. Matematica. (Seghedino) 80, 681–687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

, Akio Fujiwara e Hiroshi Imai. "Un fascio di fibre su varietà di canali quantistici e la sua applicazione alla statistica quantistica". J. fisico. R: Matematica. Teore. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

, B. M. Escher, R. L. de Matos Filho e L. Davidovich. "Quadro generale per la stima del limite ultimo di precisione nella metrologia quantistica rumorosa". Naz. Fis. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

, Rafał Demkowicz-Dobrzański, Jan Kołodyński e Mădălin Guţă. “L’inafferrabile limite di Heisenberg nella metrologia quantistica”. Naz. Comune. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

, Iman Marvian. “Interpretazione operativa delle informazioni di Fisher quantistico nella termodinamica quantistica”. Fis. Rev. Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

, Reinhard F. Werner. “Stati quantistici con correlazioni di Einstein-Podolsky-Rosen che ammettono un modello a variabili nascoste”. Fis. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

, K. Eckert, J. Schliemann, D. Bruss e M. Lewenstein. “Correlazioni quantistiche in sistemi di particelle indistinguibili”. Anna. Fis. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

, Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui e Nobuhiro Yonezawa. “Simmetria di scambio ed entanglement multipartito”. Fis. Rev.A78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

, Pawel Horodecki. “Criterio di separabilità e stati misti inseparabili con recepimento parziale positivo”. Fis. Lett. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

, Asher Peres. “Criterio di separabilità per matrici di densità”. Phys. Rev. Lett. 77, 1413–1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

, Paweł Horodecki, Michał Horodecki e Ryszard Horodecki. “L’entanglement legato può essere attivato”. Fis. Rev. Lett. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

, Géza Tóth e Tamás Vértesi. “Gli stati quantistici con trasposizione parziale positiva sono utili per la metrologia”. Fis. Rev. Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

, Scott Hill e William K. Wootters. “Entanglement di una coppia di bit quantistici”. Fis. Rev. Lett. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

, William K. Wootter. "Entanglement di formazione di uno stato arbitrario di due qubit". Fis. Rev. Lett. 80, 2245-2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

, David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal e Armin Uhlmann. “Intreccio di assistenza”. quant-ph/​9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: Quant-ph / 9803033

, John A. Smolin, Frank Verstraete e Andreas Winter. “Intreccio di assistenza e distillazione statale multipartita”. Fis. Rev.A72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

, Holger F. Hofmann e Shigeki Takeuchi. “Violazione delle relazioni di incertezza locale come segno di entanglement”. Fis. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

, Otfried Gühne. "Caratterizzare l'entanglement attraverso relazioni di incertezza". Fis. Rev. Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

, Otfried Gühne, Mátyás Mechler, Géza Tóth e Peter Adam. “I criteri di entanglement basati sulle relazioni di incertezza locale sono strettamente più forti del criterio computabile tra norme incrociate”. Fis. Rev.A74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

, Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza e Géza Tóth. "Disuguaglianze di compressione dello spin per spin arbitrario". Fis. Rev. Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

, AR Edmonds. “Momento angolare nella meccanica quantistica”. Stampa dell'Università di Princeton. (1957).
https: / / doi.org/ 10.1515 / 9781400884186 mila

, Géza Tóth. “Rilevazione di entanglement in reticoli ottici di atomi bosonici con misurazioni collettive”. Fis. Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

, Géza Tóth, Christian Knapp, Otfried Gühne e Hans J. Briegel. "Le disuguaglianze ottimali di compressione degli spin rilevano l'entanglement legato nei modelli di spin". Fis. Rev. Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

, Géza Tóth e Morgan W. Mitchell. "Generazione di stati di singoletto macroscopici in insiemi atomici". Nuovo J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

, Géza Tóth. "Rilevazione di entanglement multipartito in prossimità di stati di Dicke simmetrici". J.Opz. Soc. Sono. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

, Géza Tóth, Tobias Moroder e Otfried Gühne. "Valutazione delle misure di impigliamento del tetto convesso". Fis. Rev. Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

, Lieven Vandenberghe e Stephen Boyd. “Programmazione semidefinita”. Revisione SIAM 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003 mila

, Géza Tóth. “Entanglement multipartito e metrologia ad alta precisione”. Fis. Rev. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

, Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé e Augusto Smerzi. "Informazioni di Fisher ed entanglement multiparticellare". Fis. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

, Géza Tóth, Tamás Vértesi, Paweł Horodecki e Ryszard Horodecki. “Attivare l’utilità metrologica nascosta”. Fis. Rev. Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

, A. C. Doherty, Pablo A. Parrilo e Federico M. Spedalieri. “Distinguere gli stati separabili ed entangled”. Fis. Rev. Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

, Andrew C. Doherty, Pablo A. Parrilo e Federico M. Spedalieri. “Famiglia completa di criteri di separabilità”. Fis. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

, Andrew C. Doherty, Pablo A. Parrilo e Federico M. Spedalieri. "Rilevamento dell'entanglement multipartito". Fis. Rev.A71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

, Harold Ollivier e Wojciech H. Zurek. "Discord quantistica: una misura della quantistica delle correlazioni". Fis. Rev. Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

, L. Henderson e V. Vedral. “Correlazioni classiche, quantistiche e totali”. J. fisico. R: Matematica. Gen. 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

, Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) e Ujjwal Sen. “La discordia quantistica e i suoi alleati: una revisione dei recenti progressi”. Rep.Prog. Fis. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

, Dénes Petz. “Covarianza e informazioni di Fisher nella meccanica quantistica”. J. fisico. R: Matematica. Gen. 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

, Paolo Gibilisco, Fumio Hiai, and Dénes Petz. "Covarianza quantistica, informazione quantistica di Fisher e relazioni di incertezza". IEEE Trans. Inf. Teoria 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

, D. Petz e C. Ghinea. “Introduzione all’informazione quantistica di Fisher”. Volume 27, pagine 261–281. Mondo scientifico. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

, Frank Hansen. "Informazioni sull'inclinazione corretta metrica". Proc. Natl. Accade. Sci. USA 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

, Paolo Gibilisco, Davide Girolami e Frank Hansen. "Un approccio unificato all'incertezza quantistica locale e al potere interferometrico mediante informazioni di distorsione metriche corrette". Entropia 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

, MATLAB. “9.9.0.1524771(r2020b)”. The MathWorks Inc. Natick, Massachusetts (2020).

, MOSEK ApS. “Il manuale degli strumenti di ottimizzazione MOSEK per MATLAB. Versione 9.0”. (2019). URL: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

, J. Löfberg. "YALMIP: un toolbox per la modellazione e l'ottimizzazione in MATLAB". Negli Atti del Convegno CACSD. Taipei, Taiwan (2004).

, Géza Tóth. “QUBIT4MATLAB V3.0: un pacchetto di programmi per la scienza dell'informazione quantistica e l'ottica quantistica per MATLAB”. Calcola. Fis. Comune. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

, Il pacchetto QUBIT4MATLAB è disponibile su https:/​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433 e sulla home page personale https:/​/​gtoth.eu/​qubit4matlab.html.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Citato da

[1] Laurent Lafleche, "Trasporto ottimale quantistico e topologie deboli", arXiv: 2306.12944, (2023).

Le citazioni sopra sono di ANNUNCI SAO / NASA (ultimo aggiornamento riuscito 2023-10-16 14:47:44). L'elenco potrebbe essere incompleto poiché non tutti gli editori forniscono dati di citazione adeguati e completi.

Impossibile recuperare Crossref citato da dati durante l'ultimo tentativo 2023-10-16 14:47:42: Impossibile recuperare i dati citati per 10.22331 / q-2023-10-16-1143 da Crossref. Questo è normale se il DOI è stato registrato di recente.

Questo documento è pubblicato in Quantum sotto il Creative Commons Attribuzione 4.0 Internazionale (CC BY 4.0) licenza. Il copyright rimane dei detentori del copyright originali come gli autori o le loro istituzioni.

Timestamp:

Di più da Diario quantistico