Basi ortonormali della quantistica estrema

Ripubblicato da Platone

Seguaci: 0

Marcin Rudziński^1,2, Adam Burchardt³e Karol Zyczkowski^1,4

¹Facoltà di Fisica, Astronomia e Informatica Applicata, Università Jagellonica, ul. Łojasiewicza 11, 30-348 Cracovia, Polonia
²Scuola di dottorato in scienze esatte e naturali, Università Jagellonica, ul. Łojasiewicza 11, 30-348 Cracovia, Polonia
³QuSoft, CWI e Università di Amsterdam, Science Park 123, 1098 XG Amsterdam, Paesi Bassi
⁴Center for Theoretical Physics, Accademia polacca delle scienze, Al. Lotników 32/46, 02-668 Warszawa, Polonia

Trovi questo documento interessante o vuoi discuterne? Scrivi o lascia un commento su SciRate.

Astratto

Gli stati anticoerenti di spin hanno recentemente acquisito molta attenzione in quanto sono gli stati più “quantici”. Alcuni stati di spin coerenti e anticoerenti sono noti come rotosensori quantistici ottimali. In questo lavoro, introduciamo una misura della quanticità per basi ortonormali di stati di spin, determinata dall'anticoerenza media dei singoli vettori e dall'entropia di Wehrl. In questo modo, identifichiamo gli stati più coerenti e quantistici, che portano a misurazioni ortogonali di quantistica estrema. Le loro simmetrie possono essere rivelate utilizzando la rappresentazione stellare di Majorana, che fornisce una rappresentazione geometrica intuitiva di uno stato puro mediante punti su una sfera. I risultati ottenuti portano a basi entangled massimamente (minimamente) nel sottospazio simmetrico dimensionale $2j+1$ dello spazio dimensionale $2^{2j}$ degli stati di sistemi multipartiti composti da qubit $2j$. Alcune basi trovate sono isocoerenti poiché sono costituite da tutti gli stati con lo stesso grado di coerenza di spin.

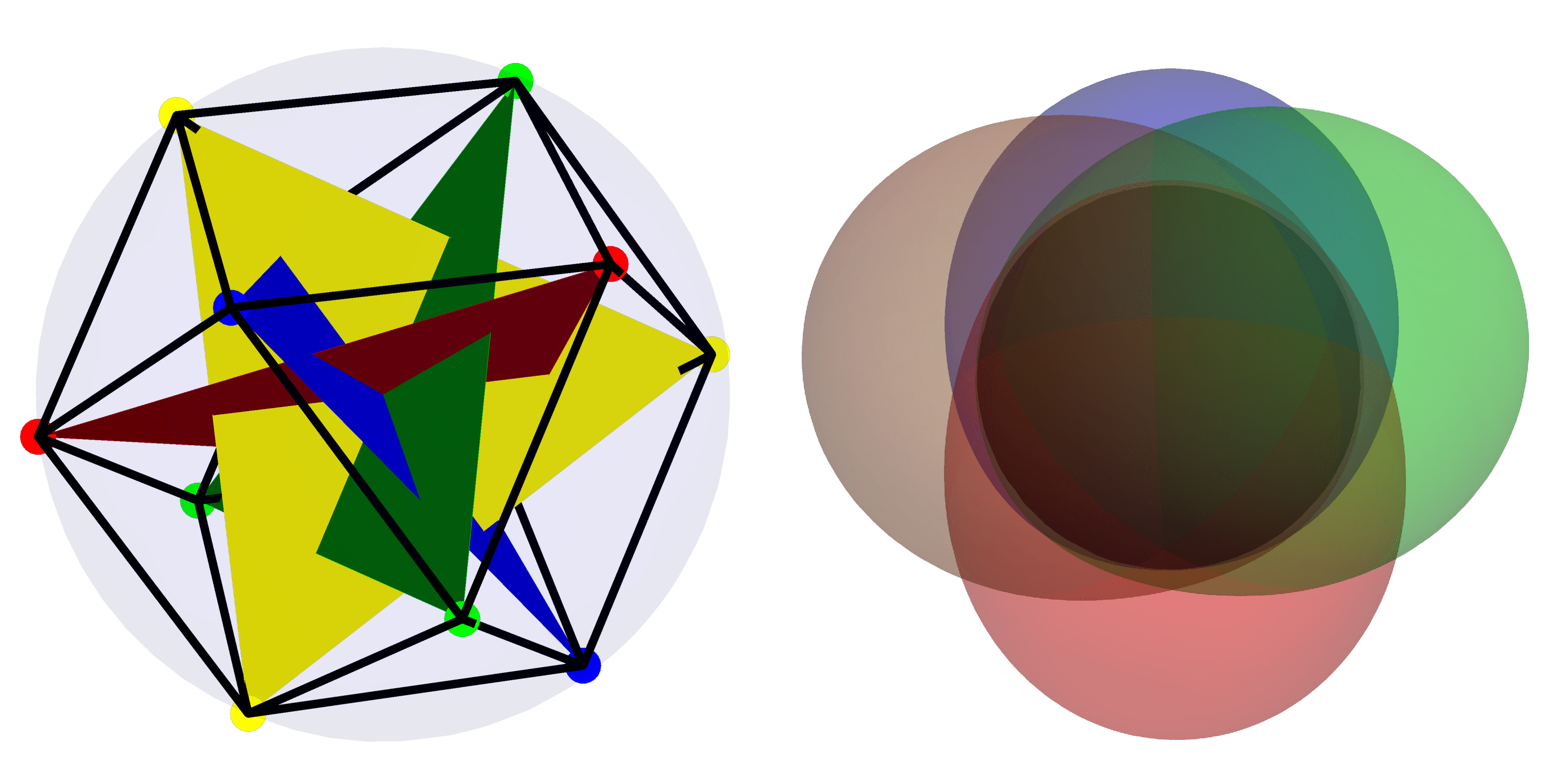
Immagine in primo piano: nell'immagine a sinistra, la base più “quantistica” in $mathcal{H}_4$ è rappresentata utilizzando la rappresentazione stellare. A destra, viene presentata la funzione Husimi per gli stati nella base più coerente (“classica”) all'interno di $mathcal{H}_4$.

Riepilogo popolare

Extremal states, coherent and anticoherent, have practical applications in quantum metrology as optimal rotosensors. This work provides a natural extension of previous studies concerning the search for such states proposing optimal orthogonal measurements of Lüders and von Neumann of the extreme spin coherence. We introduce the measure $mathcal{B}_t$ as the tool to characterize the quantumness of a measurement given by a basis in $mathcal{H}_N$. The search for the most quantum bases for $N=3,4,5$ and $7$ is performed. Numerical results suggest, that the obtained solutions are unique. A set of candidates for the “classical” bases consisting of the most spin-coherent states is indicated for $N=3,4,5,6$. Some of the most quantum bases, analyzed in the stellar representation of Majorana, reveal symmetries of Platonic solids. Most classical bases display symmetric structures too. We also considered other measures of the quantumness of vectors forming a given basis. Optimization of the mean Wehrl entropy of $N$ orthogonal vectors leads to the same bases distinguished by extremal values of the quantities $mathcal{B}_t$, with a single exception of the quantum basis for $N=6$.

► dati BibTeX

@article{Rudzinski2024orthonormalbasesof, doi = {10.22331/q-2024-01-25-1234}, url = {https://doi.org/10.22331/q-2024-01-25-1234}, title = {Orthonormal bases of extreme quantumness}, author = {Rudzi{‘{n}}ski, Marcin and Burchardt, Adam and {.{Z}}yczkowski, Karol}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {8}, pages = {1234}, month = jan, year = {2024} }

► Riferimenti

, T. Frankel, La geometria della fisica: un'introduzione, 3a ed., Cambridge University Press (2011).
https: / / doi.org/ 10.1017 / CBO9781139061377

, D. Chruściński e A. Jamiołkowski, Fasi geometriche nella meccanica classica e quantistica, Birkhäuser (2004).
https://doi.org/10.1007/978-0-8176-8176-0

, DA Lee, Relatività geometrica, American Mathematical Society, Providence (2021).
https: / / doi.org/ 10.1090 / gsm / 201

, I. Bengtsson e K. Życzkowski, Geometry of Quantum States: An Introduction to Quantum Entanglement, 2a ed., Cambridge University Press (2017).
https: / / doi.org/ 10.1017 / 9781139207010 mila

, M. Lewin, Metodi geometrici per sistemi quantistici a molti corpi non lineari, J. Functional Analysis 260, 12, (2011).
https: / / doi.org/ 10.1016 / j.jfa.2010.11.017

, E. Cohen, H. Larocque, F. Bouchard et al., Fase geometrica da Aharonov-Bohm a Pancharatnam-Berry e oltre, Nat. Rev. Fis. 1, 437–449 (2019).
https://doi.org/10.1038/s42254-019-0071-1

, E. Majorana Atomi orientati in campo magnetico variabile, Nuovo Cimento 9, 43-50 (1932).
https: / / doi.org/ 10.1007 / BF02960953

, R. Barnett, A. Turner ed E. Demler, Classificazione delle nuove fasi degli atomi spinorici, Phys. Rev. Lett. 97, 180412 (2006).
https: / / doi.org/ 10.1103 / PhysRevLett.97.180412

, R. Barnett, A. Turner ed E. Demler, Classificazione dei vortici in $ S = 3 $ condensati di Bose-Einstein, Phys. Rev.A76, 013605 (2007).
https: / / doi.org/ 10.1103 / PhysRevA.76.013605

, H. Mäkelä e K.-A. Suominen, Stati inerti dei sistemi di spin, Phys. Rev. Lett. 99, 190408 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.190408

, E. Serrano-Ensástiga e F. Mireles, Caratterizzazione di fase dei condensati di Bose-Einstein dello spinore: un approccio di rappresentazione stellare di Majorana, Phys. Lett. A492, 129188 (2023).
https: / / doi.org/ 10.1016 / j.physleta.2023.129188

, P. Mathonet et al., Equivalenza di entanglement di stati simmetrici $ N $ -qubit, Phys. Rev. A 81, 052315 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.052315

, J. Martin, O. Giraud, PA Braun, D. Braun e T. Bastin, Stati simmetrici multiqubit con elevato entanglement geometrico, Phys. Rev. A 81, 062347 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.062347

, M. Aulbach, DJH Markham e M. Murao, Lo stato simmetrico massimamente entangled in termini di misura geometrica, New J. Phys. 12, 073025 (2010).
https://doi.org/10.1088/1367-2630/12/7/073025

, DJH Markham, Entanglement e simmetria negli stati simmetrici per permutazione, Phys. Rev. A 83, 042332 (2011).
https: / / doi.org/ 10.1103 / PhysRevA.83.042332

, P. Ribeiro e R. Mosseri, Entanglement nel settore simmetrico di $n$ qubits, Phys. Rev. Lett. 106, 180502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.106.180502

, M.Aulbach, Classificazione dell'entanglement in stati simmetrici, Int. J. Informazioni quantistiche. 10, 1230004 (2012).
https: / / doi.org/ 10.1142 / S0219749912300045

, W. Ganczarek, M. Kuś e K. Życzkowski, Misura baricentrica dell'entanglement quantistico, Phys. Rev. A 85, 032314 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.032314

, A. Mandilara, T. Coudreau, A. Keller e P. Milman, Classificazione dell'entanglement di stati simmetrici puri tramite stati coerenti di spin, Phys. Rev. A 90, 050302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.050302

, P. Hyllus, al., Informazioni di Fisher ed entanglement multiparticellare, Phys. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

, JH Hannay, La fase Berry per lo spin nella rappresentazione di Majorana, J. Phys. R: Matematica. Gen. 31, L53 (1998).
https://doi.org/10.1088/0305-4470/31/2/002

, P. Bruno, Fase geometrica quantistica nella rappresentazione stellare di Majorana: mappatura su una fase Aharonov-Bohm a molti corpi, Phys. Rev. Lett. 108, 240402 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.240402

, HD Liu e LB Fu, Fase Berry ed entanglement quantistico nella rappresentazione stellare di Majorana, Phys. Rev. A 94, 022123 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.022123

, P. Ribeiro, J. Vidal e R. Mosseri, Limite termodinamico del modello Lipkin-Meshkov-Glick, Phys. Rev. Lett. 99, 050402 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.050402

, P. Ribeiro, J. Vidal e R. Mosseri, Spettro esatto del modello Lipkin-Meshkov-Glick nel limite termodinamico e correzioni di dimensione finita, Phys. Rev. E 78, 021106 (2008).
https: / / doi.org/ 10.1103 / PhysRevE.78.021106

, J. Zimba, Stati di spin “Anticoerente” tramite la Rappresentazione di Majorana, Electron. J. Teore. Fis. 3, 143 (2006).
https:///api.semanticscholar.org/CorpusID:13938120

, D. Baguette, T. Bastin e J. Martin, Stati simmetrici multiqubit con riduzioni al massimo di un qubit miste, Phys. Rev. A 90, 032314 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.032314

, O. Giraud, D. Braun, D. Baguette, T. Bastin e J. Martin, rappresentazione tensoriale degli stati di spin, Phys. Rev. Lett. 114, 080401 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.080401

, D. Baguette, F. Damanet, O. Giraud e J. Martin, Anticoherence degli stati di spin con simmetrie punto-gruppo, Phys. Rev. A 92, 052333 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.92.052333

, HD Liu, LB Fu, X. Wang, Approccio dello stato coerente per la rappresentazione di Majorana, Commun. Teore. Fis. 67, 611 (2017).
https://doi.org/10.1088/0253-6102/67/6/611

, D. Baguette e J. Martin, Misure di anticoerenza per stati di spin puri, Phys. Rev. A 96, 032304 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.032304

, P. Kolenderski e R. Demkowicz-Dobrzański, Stato ottimale per mantenere allineati i sistemi di riferimento e i solidi platonici, Phys. Rev.A78, 052333 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052333

, C. Chryssomalakos e H. Hernández-Coronado, Rotosensori quantistici ottimali, Phys. Rev. A 95, 052125 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.95.052125

, AZ Goldberg e DFV James, Misurazioni dell'angolo di Eulero limitato quantistico utilizzando stati anticoerenti, Phys. Rev. A 98, 032113 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032113

, J. Martin, S. Weigert e O. Giraud, Rilevamento ottimale di rotazioni attorno ad assi sconosciuti da parte di stati coerenti e anticoerenti, Quantum 4, 285 (2020).
https://doi.org/10.22331/q-2020-06-22-285

, J. Crann, DW Kribs e R. Pereira, Disegni sferici e stati di spin anticoerenti, J. Phys. R: Matematica. Teore. 43, 255307 (2010).
https://doi.org/10.1088/1751-8113/43/25/255307

, E. Bannai e M. Tagami, Una nota sugli stati di spin anticoerenti, J. Phys. R: Matematica. Teore. 44, 342002 (2011).
https://doi.org/10.1088/1751-8113/44/34/342002

, M. Wang e Y. Zhu, Stati spin-2 anticoerenti e disegni sferici, J. Phys. R: Matematica. Teore. 55, 425304 (2022).
https:///doi.org/10.1088/1751-8121/ac971d

, AZ Goldberg, AB Klimov, M.Grassl, G. Leuchs e LL Sánchez-Soto, Stati quantistici estremi, AVS Quantum Sci. 2, 044701 (2020).
https: / / doi.org/ 10.1116 / 5.0025819 mila

, AZ Goldberg, M. Grassl, G. Leuchs e LL Sánchez-Soto, Quantumness beyond entanglement: il caso degli stati simmetrici, Phys. Rev. A 105, 022433 (2022).
https: / / doi.org/ 10.1103 / PhysRevA.105.022433

, O. Giraud, P. Braun e D. Braun, Quantificare la quantistica e la ricerca di Queens of Quantum, New J. Phys. 12, 063005 (2010).
https://doi.org/10.1088/1367-2630/12/6/063005

, R. Delbourgo, Stati di incertezza minima per il gruppo di rotazione e i gruppi affini, J. Phys. A10, L233 (1977).
https://doi.org/10.1088/0305-4470/10/11/012

, A. Wehrl, Sul rapporto tra entropia classica e quantomeccanica, Rep. Math. Fis. 16, 353 (1979).
https://doi.org/10.1016/0034-4877(79)90070-3

, EH Lieb, Prova di una congettura entropica di Wehrl, Commun. Matematica. Fis. 62, 35 (1978).
https: / / doi.org/ 10.1007 / BF01940328

, CT Lee, entropia degli stati di spin di Wehrl e congettura di Lieb, J. Phys. A21, 3749 (1988).
https://doi.org/10.1088/0305-4470/21/19/013

, EH Lieb e JP Solovej, Prova di una congettura entropica per stati di spin coerenti di Bloch e sue generalizzazioni, Acta Math. 212, 379 (2014).
https://doi.org/10.1007/s11511-014-0113-6

, F. Bouchard, al., Metrologia quantistica al limite con costellazioni di Majorana estrema, Optica 4, 1429-1432 (2017).
https: / / doi.org/ 10.1364 / OPTICA.4.001429

, A. Wehrl, Proprietà generali dell'entropia, Rev. Mod. Fis. 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

, A. Wehrl, Le molteplici sfaccettature dell'entropia, Rep. Math. Fis. 30, 119 (1991).
https://doi.org/10.1016/0034-4877(91)90045-O

, S. Gnutzmann e K. Życzkowski, Entropie di Renyi-Wehrl come misure di localizzazione nello spazio delle fasi, J. Phys. A34, 10123 (2001).
https://doi.org/10.1088/0305-4470/34/47/317

, K. Życzkowski, Localizzazione degli autostati ed entropia media di Wehrl, Physica E 9, 583 (2001).
https://doi.org/10.1016/S1386-9477(00)00266-6

, LL Sánchez-Soto, AB Klimov, P. de la Hoz e G. Leuchs, Quantistici contro stati di polarizzazione classica: quando contano i multipoli, J. Phys. B46 (104011).
https://doi.org/10.1088/0953-4075/46/10/104011

, A. Tavakoli e N. Gisin, I solidi platonici e i test fondamentali della meccanica quantistica, Quantum 4, 293 (2020).
https://doi.org/10.22331/q-2020-07-09-293

, H.Ch. Nguyen, S. Designolle, M. Barakat e O. Gühne, Simmetrie tra misurazioni nella meccanica quantistica, prestampa arXiv:2003.12553 (2022).
https:///doi.org/10.48550/arXiv.2003.12553
arXiv: 2003.12553

, JI Latorre e G. Sierra, entanglement platonico, Quantum Inf. Calcola. 21, 1081 (2021).
https: / / doi.org/ 10.26421 / QIC21.13-14-1

, K. Bolonek-Lasoń e P. Kosiński, Gruppi, solidi platonici e disuguaglianze di Bell, Quantum 5, 593 (2021).
https://doi.org/10.22331/q-2021-11-29-593

, KF Pál e T. Vértesi, Gruppi, disuguaglianze di campana platonica per tutte le dimensioni, Quantum 6, 756 (2022).
https://doi.org/10.22331/q-2022-07-07-756

, RH Dicke, Coerenza nei processi di radiazione spontanei, Phys. Rev. 93, 99 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99

, V. Karimipour e L. Memarzadeh, Basi equientangolate in dimensioni arbitrarie Phys. Rev.A73, 012329 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.73.012329

, G. Rajchel, A. Gąsiorowski e K. Życzkowski, Matrici robuste di Hadamard, raggi unistocastici nel politopo di Birkhoff e basi equientangled in spazi compositi Matematica. Comp. Sci. 12, 473 (2018).
https: / / doi.org/ 10.1007 / s11786-018-0384-y

, J. Czartowski, D. Goyeneche, M. Grassl e K. Życzkowski, Basi isoentangled reciprocamente imparziali, misurazioni quantistiche simmetriche e progetti a stati misti, Phys. Rev. Lett. 124, 090503 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.124.090503

, F. Del Santo, J. Czartowski, K. Życzkowski e N. Gisin, Basi iso-entangled e misurazioni congiunte, preprint arXiv:2307.06998 (2023).
https:///doi.org/10.48550/arXiv.2307.06998
arXiv: 2307.06998

, R. Penrose, On Bell non-località senza probabilità: qualche geometria curiosa, Quantum Reflections (2000).

, J. Zimba e R. Penrose, On Bell non-località senza probabilità: geometria più curiosa, Stud. Storia. Fil. Sci. 24, 697 (1993).
https://doi.org/10.1016/0039-3681(93)90061-N

, JE Massad e PK Aravind, Il dodecaedro di Penrose rivisitato, Am. J. Fisica 67, 631 (1999).
https: / / doi.org/ 10.1119 / 1.19336 mila

, K. Husimi, Alcune proprietà formali della matrice di densità, Proc. Fis. Matematica. Soc. 22, 264 (1940).
https: / / doi.org/ 10.11429 / ppmsj1919.22.4_264

, W. Słomczyński e K. Życzkowski, Entropia dinamica media delle mappe quantistiche sulla sfera diverge nel limite semiclassico, Phys. Rev. Lett. 80, 1880 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.1880

, M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, Goniometri quantici perfetti, preprint arXiv:2310.13045 (2023).
https:///doi.org/10.48550/arXiv.2310.13045
arXiv: 2310.13045

, NCN Maestro 7 2015/18/A/ST2/00274 sito web https://chaos.if.uj.edu.pl/ karol/Maestro7/files/data3/Numerical_Results.dat.
https:///chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

, D. Weingarten, Comportamento asintotico degli integrali di gruppo nel limite di rango infinito, J. Math. Fis. 19, 999 (1978).
https: / / doi.org/ 10.1063 / 1.523807 mila

, B. Collins e P. Śniady, Integrazione rispetto alla misura Haar sul gruppo unitario, ortogonale e simplettico, Commun. Matematica. Fis. 264, 773 (2006).
https://doi.org/10.1007/s00220-006-1554-3

, G. Rajchel, Mappature e progetti quantistici, tesi di dottorato, prestampa arXiv:2204.13008 (2022).
https:///doi.org/10.48550/arXiv.2204.13008
arXiv: 2204.13008

, D. Martin e EP Wigner, Teoria dei gruppi e sua applicazione alla meccanica quantistica degli spettri atomici, Academic Press Inc. NY (1959).
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

Citato da

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny e Kamil Korzekwa, “Goniometri quantistici perfetti”, arXiv: 2310.13045, (2023).

[2] Aaron Z. Goldberg, "Correlazioni per sottoinsiemi di particelle in stati simmetrici: cosa fanno i fotoni all'interno di un raggio di luce quando il resto viene ignorato", arXiv: 2401.05484, (2024).

Le citazioni sopra sono di ANNUNCI SAO / NASA (ultimo aggiornamento riuscito 2024-01-25 11:53:23). L'elenco potrebbe essere incompleto poiché non tutti gli editori forniscono dati di citazione adeguati e completi.

Impossibile recuperare Crossref citato da dati durante l'ultimo tentativo 2024-01-25 11:53:22: Impossibile recuperare i dati citati per 10.22331 / q-2024-01-25-1234 da Crossref. Questo è normale se il DOI è stato registrato di recente.

Questo documento è pubblicato in Quantum sotto il Creative Commons Attribuzione 4.0 Internazionale (CC BY 4.0) licenza. Il copyright rimane dei detentori del copyright originali come gli autori o le loro istituzioni.

Distribuzione di contenuti basati su SEO e PR. Ricevi amplificazione oggi.
PlatoData.Network Generativo verticale Ai. Potenzia te stesso. Accedi qui.
PlatoAiStream. Intelligenza Web3. Conoscenza amplificata. Accedi qui.
PlatoneESG. Carbonio, Tecnologia pulita, Energia, Ambiente, Solare, Gestione dei rifiuti. Accedi qui.
Platone Salute. Intelligence sulle biotecnologie e sulle sperimentazioni cliniche. Accedi qui.
Fonte: https://quantum-journal.org/papers/q-2024-01-25-1234/

Timestamp: Gennaio 25, 2024

Timestamp: Ottobre 25, 2023

Basi ortonormali di quantistica estrema

Ripubblicato da Platone

Astratto

Riepilogo popolare

► dati BibTeX

► Riferimenti

Citato da

Di più da Diario quantistico

Perfetta corrispondenza del peso minimo correlato in pipeline del codice di superficie

Banditi quantistici multi-armati: esplorazione contro sfruttamento durante l'apprendimento delle proprietà degli stati quantistici

Classificazione del filo quantico basato sulla misurazione nello stabilizzatore PEPS

Integrazione Quantum Monte Carlo: il massimo vantaggio in una profondità minima del circuito

Protocolli DIQKD migliorati con analisi a dimensione finita

Progettazioni di stati quantistici emergenti e biunitarietà nella dinamica dei circuiti duali-unitari

Codici LDPC quantistici su misura per il bias

Metodo di Lanczos esatto ed efficiente su un computer quantistico

La dinamica causale implica interazioni locali?

Sui test della natura quantistica delle interazioni gravitazionali in presenza di correzioni non lineari alla meccanica quantistica

Chi siamo

Ricerca verticale e Ai

Piattaforma

Rimani in contatto

Il mio account