Az extrém kvantum ortonormális alapjai

Újra kiadta Platón

Követő: 0

Marcin Rudziński^1,2, Adam Burchardt³és Karol Życzkowski^1,4

¹Fizikai, Csillagászati és Alkalmazott Számítástechnikai Kar, Jagelló Egyetem, ul. Łojasiewicza 11, 30-348 Krakkó, Lengyelország
²Pontos és Természettudományi Doktori Iskola, Jagelló Egyetem, ul. Łojasiewicza 11, 30-348 Krakkó, Lengyelország
³QuSoft, CWI és Amszterdami Egyetem, Science Park 123, 1098 XG Amsterdam, Hollandia
⁴Elméleti Fizikai Központ, Lengyel Tudományos Akadémia, Al. Lotników 32/46, 02-668 Warszawa, Lengyelország

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

A spin antikoherens állapotok az utóbbi időben nagy figyelmet kaptak, mint a leginkább „kvantum” állapotok. Néhány koherens és antikoherens spinállapot optimális kvantum rotoszenzorként ismert. Ebben a munkában bemutatjuk a spinállapotok ortonormális bázisainak kvantumát, amelyet az egyes vektorok átlagos antikoherenciája és a Wehrl-entrópia határoz meg. Ily módon azonosítjuk a legkoherensebb és leginkább kvantumállapotokat, amelyek a szélsőséges kvantum ortogonális méréséhez vezetnek. Szimmetriájuk a Majorana csillagábrázolással tárható fel, amely a tiszta állapot intuitív geometriai ábrázolását adja a gömb pontjai alapján. A kapott eredmények maximálisan (minimálisan) összefonódott bázisokhoz vezetnek a $2j$ qubitekből álló többrészes rendszerek $1^{2j}$ dimenziós szimmetrikus alterében. Egyes talált bázisok izokoherensek, mivel minden azonos fokú spin-koherenciájú állapotból állnak.

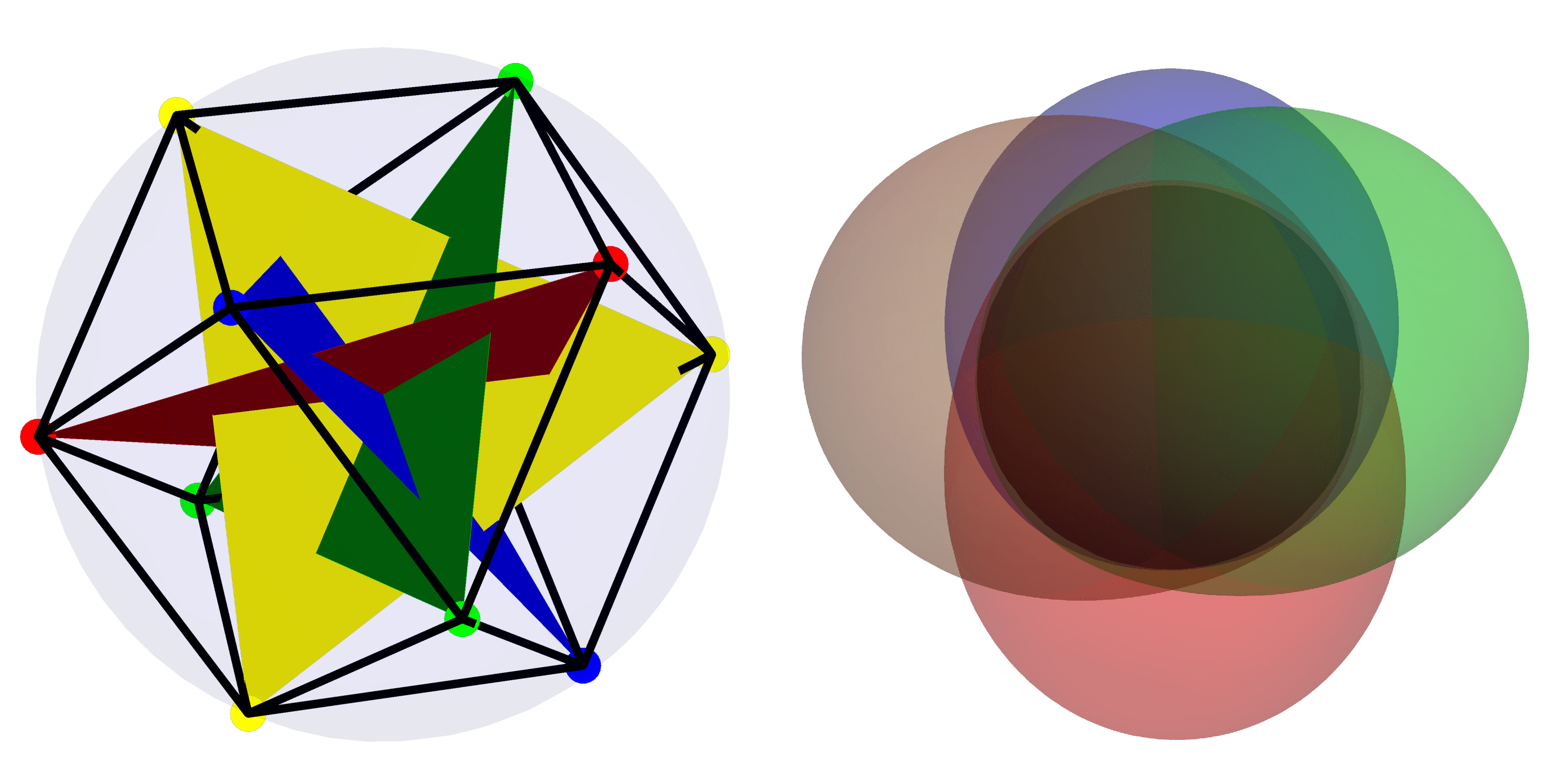
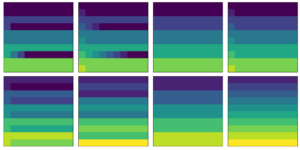
Kiemelt kép: A bal oldali képen a $mathcal{H}_4$ legkvantumosabb bázisa látható a csillagábrázolás használatával. A jobb oldalon a $mathcal{H}_4$ legkoherensebb („klasszikus”) alapú állapotaihoz tartozó Husimi-függvény látható.

Népszerű összefoglaló

Extremal states, coherent and anticoherent, have practical applications in quantum metrology as optimal rotosensors. This work provides a natural extension of previous studies concerning the search for such states proposing optimal orthogonal measurements of Lüders and von Neumann of the extreme spin coherence. We introduce the measure $mathcal{B}_t$ as the tool to characterize the quantumness of a measurement given by a basis in $mathcal{H}_N$. The search for the most quantum bases for $N=3,4,5$ and $7$ is performed. Numerical results suggest, that the obtained solutions are unique. A set of candidates for the “classical” bases consisting of the most spin-coherent states is indicated for $N=3,4,5,6$. Some of the most quantum bases, analyzed in the stellar representation of Majorana, reveal symmetries of Platonic solids. Most classical bases display symmetric structures too. We also considered other measures of the quantumness of vectors forming a given basis. Optimization of the mean Wehrl entropy of $N$ orthogonal vectors leads to the same bases distinguished by extremal values of the quantities $mathcal{B}_t$, with a single exception of the quantum basis for $N=6$.

► BibTeX adatok

@article{Rudzinski2024orthonormalbasesof, doi = {10.22331/q-2024-01-25-1234}, url = {https://doi.org/10.22331/q-2024-01-25-1234}, title = {Orthonormal bases of extreme quantumness}, author = {Rudzi{‘{n}}ski, Marcin and Burchardt, Adam and {.{Z}}yczkowski, Karol}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {8}, pages = {1234}, month = jan, year = {2024} }

► Referenciák

[1] T. Frankel, The Geometry of Physics: An Introduction, 3. kiadás, Cambridge University Press (2011).
https:///doi.org/10.1017/CBO9781139061377

[2] D. Chruściński és A. Jamiołkowski, Geometric Phases in Classical and Quantum Mechanics, Birkhäuser (2004).
https://doi.org/10.1007/978-0-8176-8176-0

[3] DA Lee, Geometriai relativitáselmélet, Amerikai Matematikai Társaság, Providence (2021).
https:///doi.org/10.1090/gsm/201

[4] I. Bengtsson és K. Życzkowski, Geometry of Quantum States: An Introduction to Quantum Entanglement, 2. kiadás, Cambridge University Press (2017).
https:///doi.org/10.1017/9781139207010

[5] M. Lewin: Geometriai módszerek nemlineáris soktestű kvantumrendszerekhez, J. Functional Analysis 260, 12, (2011).
https:///doi.org/10.1016/j.jfa.2010.11.017

[6] E. Cohen, H. Larocque, F. Bouchard és munkatársai, Geometrikus fázis Aharonov–Bohmtól Pancharatnam–Berry-ig és tovább, Nat. Rev. Phys. 1, 437–449 (2019).
https://doi.org/10.1038/s42254-019-0071-1

[7] E. Majorana Atomi orientati in campo magnetico változó, Nuovo Cimento 9, 43-50 (1932).
https:///doi.org/10.1007/BF02960953

[8] R. Barnett, A. Turner és E. Demler, Classifying novel phases of spinor atoms, Phys. Rev. Lett. 97, 180412 (2006).
https:///doi.org/10.1103/PhysRevLett.97.180412

[9] R. Barnett, A. Turner és E. Demler, Az örvények osztályozása $S=3$ Bose-Einstein kondenzátumokban, Phys. Rev. A 76, 013605 (2007).
https:///doi.org/10.1103/PhysRevA.76.013605

[10] H. Mäkelä és K.-A. Suominen, Spin-s rendszerek inert állapotai, Phys. Rev. Lett. 99, 190408 (2007).
https:///doi.org/10.1103/PhysRevLett.99.190408

[11] E. Serrano-Ensástiga és F. Mireles, Phase characterization of spinor Bose-Einstein condensates: a Majorana stellar representation approach, Phys. Lett. A 492, 129188 (2023).
https:///doi.org/10.1016/j.physleta.2023.129188

[12] P. Mathonet és munkatársai, $N$-qubit szimmetrikus állapotok összefonódási ekvivalenciája, Phys. Rev. A 81, 052315 (2010).
https:///doi.org/10.1103/PhysRevA.81.052315

[13] J. Martin, O. Giraud, PA Braun, D. Braun és T. Bastin, Multiqubit szimmetrikus állapotok nagy geometriai összefonódással, Phys. Rev. A 81, 062347 (2010).
https:///doi.org/10.1103/PhysRevA.81.062347

[14] M. Aulbach, DJH Markham és M. Murao, A maximálisan összefonódott szimmetrikus állapot a geometriai mérték szempontjából, New J. Phys. 12, 073025 (2010).
https://doi.org/10.1088/1367-2630/12/7/073025

[15] DJH Markham, Összefonódás és szimmetria permutáció-szimmetrikus állapotokban, Phys. Rev. A 83, 042332 (2011).
https:///doi.org/10.1103/PhysRevA.83.042332

[16] P. Ribeiro és R. Mosseri, Entanglement in the symmetric szektor of $n$ qubits, Phys. Rev. Lett. 106, 180502 (2011).
https:///doi.org/10.1103/PhysRevLett.106.180502

[17] M.Aulbach, Az összefonódás osztályozása szimmetrikus állapotokban, Int. J. Quantum Inform. 10, 1230004 (2012).
https:///doi.org/10.1142/S0219749912300045

[18] W. Ganczarek, M. Kuś és K. Życzkowski, Barycentric measure of quantum enanglement, Phys. Rev. A 85, 032314 (2012).
https:///doi.org/10.1103/PhysRevA.85.032314

[19] A. Mandilara, T. Coudreau, A. Keller és P. Milman, Entanglement classification of pure symmetric states via spin koherens állapotok, Phys. Rev. A 90, 050302(R) (2014).
https:///doi.org/10.1103/PhysRevA.90.050302

[20] P. Hyllus és munkatársai, Fisher information and multipartticle entanglement, Phys. Rev. A 85, 022321 (2012).
https:///doi.org/10.1103/PhysRevA.85.022321

[21] JH Hannay, The Berry phase for spin in the Majorana reprezentáció, J. Phys. V: Matek. Gen. 31, L53 (1998).
https://doi.org/10.1088/0305-4470/31/2/002

[22] P. Bruno, Kvantumgeometriai fázis Majorana csillagábrázolásában: Leképezés sok testből álló Aharonov-Bohm fázisra, Phys. Rev. Lett. 108, 240402 (2012).
https:///doi.org/10.1103/PhysRevLett.108.240402

[23] HD Liu és LB Fu, Berry fázis és kvantumösszefonódás Majorana csillagábrázolásában, a Phys. Rev. A 94, 022123 (2016).
https:///doi.org/10.1103/PhysRevA.94.022123

[24] P. Ribeiro, J. Vidal és R. Mosseri, Thermodynamical limit of the Lipkin-Meshkov-Glick modell, Phys. Rev. Lett. 99, 050402 (2007).
https:///doi.org/10.1103/PhysRevLett.99.050402

[25] P. Ribeiro, J. Vidal és R. Mosseri: A Lipkin-Meshkov-Glick modell pontos spektruma a termodinamikai határ- és véges méretű korrekciókban, Phys. Rev. E 78, 021106 (2008).
https:///doi.org/10.1103/PhysRevE.78.021106

[26] J. Zimba, „Antikoherens” spin állapotok a Majorana-képviseleten, az Electronon keresztül. J. Theor. Phys. 3, 143 (2006).
https:///api.semanticscholar.org/CorpusID:13938120

[27] D. Baguette, T. Bastin és J. Martin, Multiqubit szimmetrikus állapotok maximálisan vegyes egy qubit redukciókkal, Phys. Rev. A 90, 032314 (2014).
https:///doi.org/10.1103/PhysRevA.90.032314

[28] O. Giraud, D. Braun, D. Baguette, T. Bastin és J. Martin: A spin állapotok tenzoros reprezentációja, Phys. Rev. Lett. 114, 080401 (2015).
https:///doi.org/10.1103/PhysRevLett.114.080401

[29] D. Baguette, F. Damanet, O. Giraud és J. Martin, Anticoherence of spin states with point-group symmetries, Phys. Rev. A 92, 052333 (2015).
https:///doi.org/10.1103/PhysRevA.92.052333

[30] HD Liu, LB Fu, X. Wang, Koherens állapotú megközelítés Majorana reprezentációjához, Commun. Theor. Phys. 67, 611 (2017).
https://doi.org/10.1088/0253-6102/67/6/611

[31] D. Baguette és J. Martin, Antikoherencia mérések tiszta spin állapotokhoz, Phys. Rev. A 96, 032304 (2017).
https:///doi.org/10.1103/PhysRevA.96.032304

[32] P. Kolenderski és R. Demkowicz-Dobrzański, Optimális állapot a referenciakeretek és a platóni szilárdtestek igazításában tartásához, Phys. Rev. A 78, 052333 (2008).
https:///doi.org/10.1103/PhysRevA.78.052333

[33] C. Chryssomalakos és H. Hernández-Coronado, Optimal quantum rotosensors, Phys. Rev. A 95, 052125 (2017).
https:///doi.org/10.1103/PhysRevA.95.052125

[34] AZ Goldberg és DFV James, Quantum-limited Euler-szög mérések antikoherens állapotok használatával, Phys. Rev. A 98, 032113 (2018).
https:///doi.org/10.1103/PhysRevA.98.032113

[35] J. Martin, S. Weigert és O. Giraud: Ismeretlen tengelyek körüli forgások optimális detektálása koherens és antikoherens állapotokkal, Quantum 4, 285 (2020).
https://doi.org/10.22331/q-2020-06-22-285

[36] J. Crann, DW Kribs és R. Pereira, Spherical designs and antikoherens spin states, J. Phys. V: Matek. Theor. 43, 255307 (2010).
https://doi.org/10.1088/1751-8113/43/25/255307

[37] E. Bannai és M. Tagami, A note on antikoherens spin states, J. Phys. V: Matek. Theor. 44, 342002 (2011).
https://doi.org/10.1088/1751-8113/44/34/342002

[38] M. Wang és Y. Zhu, Antikoherent spin-2 states and spherical designs, J. Phys. V: Matek. Theor. 55, 425304 (2022).
https:///doi.org/10.1088/1751-8121/ac971d

[39] AZ Goldberg, AB Klimov, M. Grassl, G. Leuchs és LL Sánchez-Soto, Extremal quantum states, AVS Quantum Sci. 2, 044701 (2020).
https:///doi.org/10.1116/5.0025819

[40] AZ Goldberg, M. Grassl, G. Leuchs és LL Sánchez-Soto, Quantumness into Enanglement: The case of symmetric states, Phys. Rev. A 105, 022433 (2022).
https:///doi.org/10.1103/PhysRevA.105.022433

[41] O. Giraud, P. Braun és D. Braun, Quantifying quantumness and the Queens of Quantum, New J. Phys. 12, 063005 (2010).
https://doi.org/10.1088/1367-2630/12/6/063005

[42] R. Delbourgo, Minimális bizonytalansági állapotok a rotációs csoportra és a rokon csoportokra, J. Phys. A 10, L233 (1977).
https://doi.org/10.1088/0305-4470/10/11/012

[43] A. Wehrl, A klasszikus és a kvantummechanikai entrópia kapcsolatáról, Rep. Math. Phys. 16, 353 (1979)].
https://doi.org/10.1016/0034-4877(79)90070-3

[44] EH Lieb, Wehrl entrópiasejtésének bizonyítása, Commun. Math. Phys. 62, 35 (1978)].
https:///doi.org/10.1007/BF01940328

[45] CT Lee, Wehrl spinállapotok entrópiája és Lieb sejtése, J. Phys. A 21, 3749 (1988).
https://doi.org/10.1088/0305-4470/21/19/013

[46] EH Lieb és JP Solovej, Bloch koherens spinállapotok entrópia-sejtésének bizonyítása és általánosításai, Acta Math. 212, 379 (2014).
https://doi.org/10.1007/s11511-014-0113-6

[47] F. Bouchard, és munkatársai, Quantum metrology at the limit with extremal Majorana konstellációk, Optica 4, 1429-1432 (2017).
https:///doi.org/10.1364/OPTICA.4.001429

[48] A. Wehrl, Az entrópia általános tulajdonságai, Rev. Mod. Phys. 50, 221 (1978)].
https:///doi.org/10.1103/RevModPhys.50.221

[49] A. Wehrl, Az entrópia sokféle aspektusa, Rep. Math. Phys. 30, 119 (1991)].
https://doi.org/10.1016/0034-4877(91)90045-O

[50] S. Gnutzmann és K. Życzkowski, Renyi-Wehrl entrópiák mint a lokalizáció mértéke a fázistérben, J. Phys. A 34, 10123 (2001).
https://doi.org/10.1088/0305-4470/34/47/317

[51] K. Życzkowski, A sajátállapotok lokalizációja és az átlagos Wehrl-entrópia, Physica E 9, 583 (2001).
https://doi.org/10.1016/S1386-9477(00)00266-6

[52] LL Sánchez-Soto, AB Klimov, P. de la Hoz és G. Leuchs, Quantum versus classical polarization states: when multipoles count, J. Phys. B 46 104011 (2013).
https://doi.org/10.1088/0953-4075/46/10/104011

[53] A. Tavakoli és N. Gisin, The Platonic solids and basic tests of quantum mechanics, Quantum 4, 293 (2020).
https://doi.org/10.22331/q-2020-07-09-293

[54] H.Ch. Nguyen, S. Designolle, M. Barakat és O. Gühne, Szimmetriák a mérések között a kvantummechanikában, preprint arXiv:2003.12553 (2022).
https:///doi.org/10.48550/arXiv.2003.12553
arXiv: 2003.12553

[55] JI Latorre és G. Sierra, Platonic Enanglement, Quantum Inf. Comput. 21, 1081 (2021).
https:///doi.org/10.26421/QIC21.13-14-1

[56] K. Bolonek-Lasoń és P. Kosiński, Csoportok, platóni szilárdtestek és Bell-egyenlőtlenségek, Quantum 5, 593 (2021).
https://doi.org/10.22331/q-2021-11-29-593

[57] KF Pál, és T. Vértesi, Csoportok, Platonic Bell egyenlőtlenségek minden dimenzióra, Quantum 6, 756 (2022).
https://doi.org/10.22331/q-2022-07-07-756

[58] RH Dicke, Koherencia spontán sugárzási folyamatokban, Phys. Rev. 93, 99 (1954).
https:///doi.org/10.1103/PhysRev.93.99

[59] V. Karimipour és L. Memarzadeh, Equientangled bázisok tetszőleges méretekben Phys. Rev. A 73, 012329 (2006).
https:///doi.org/10.1103/PhysRevA.73.012329

[60] G. Rajchel, A. Gąsiorowski és K. Życzkowski: Robusztus Hadamard-mátrixok, unisztochasztikus sugarak Birkhoff-politópban és equi-entangled bázisok összetett terekben Math. Összeg. Sci. 12, 473 (2018).
https:///doi.org/10.1007/s11786-018-0384-y

[61] J. Czartowski, D. Goyeneche, M. Grassl és K. Życzkowski, Isoentangled kölcsönösen elfogulatlan bázisok, szimmetrikus kvantummérések és vegyes állapotú tervek, Phys. Rev. Lett. 124, 090503 (2020).
https:///doi.org/10.1103/PhysRevLett.124.090503

[62] F. Del Santo, J. Czartowski, K. Życzkowski és N. Gisin, Iso-entangled bases and joint mérések, preprint arXiv:2307.06998 (2023).
https:///doi.org/10.48550/arXiv.2307.06998
arXiv: 2307.06998

[63] R. Penrose, On Bell nem lokalitás valószínűségek nélkül: néhány érdekes geometria, Quantum Reflections (2000).

[64] J. Zimba és R. Penrose, On Bell nem lokalitás valószínűségek nélkül: További érdekes geometria, Stud. Hist. Phil. Sci. 24, 697 (1993).
https://doi.org/10.1016/0039-3681(93)90061-N

[65] JE Massad és PK Aravind, The Penrose dodekaéder újra, Am. J. Physics 67, 631 (1999).
https:///doi.org/10.1119/1.19336

[66] K. Husimi, Néhány formális tulajdonság a sűrűségmátrixról, Proc. Phys. Math. Soc. 22, 264 (1940).
https:///doi.org/10.11429/ppmsj1919.22.4_264

[67] W. Słomczyński és K. Życzkowski: Kvantumtérképek átlagos dinamikus entrópiája a gömbön diverges a félklasszikus határértékben, Phys. Rev. Lett. 80, 1880 (1998).
https:///doi.org/10.1103/PhysRevLett.80.1880

[68] M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, Perfect quantum protractors, preprint arXiv:2310.13045 (2023).
https:///doi.org/10.48550/arXiv.2310.13045
arXiv: 2310.13045

[69] Az NCN Maestro 7 2015/18/A/ST2/00274 webhely https://chaos.if.uj.edu.pl/karol/Maestro7/files/data3/Numerical_Results.dat.
https:///chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

[70] D. Weingarten, Csoportintegrálok aszimptotikus viselkedése a végtelen rang határában, J. Math. Phys. 19, 999 (1978).
https:///doi.org/10.1063/1.523807

[71] B. Collins és P. Śniady, Integration with Respect to the Haar Measure on Unitary, Orthogonal and Symplectic Group, Commun. Math. Phys. 264, 773 (2006).
https://doi.org/10.1007/s00220-006-1554-3

[72] G. Rajchel, Quantum mappings and designs, PhD Thesis, preprint arXiv:2204.13008 (2022).
https:///doi.org/10.48550/arXiv.2204.13008
arXiv: 2204.13008

[73] D. Martin és EP Wigner, Csoportelmélet és alkalmazása az atomspektrumok kvantummechanikájára, Academic Press Inc. NY (1959).
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

Idézi

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny és Kamil Korzekwa, „Tökéletes kvantumszögmérők”, arXiv: 2310.13045, (2023).

[2] Aaron Z. Goldberg, „Korrelációk a szimmetrikus állapotú részecskék részhalmazaihoz: mit csinálnak a fotonok egy fénysugáron belül, ha a többit figyelmen kívül hagyjuk” arXiv: 2401.05484, (2024).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2024-01-25 11:53:23). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

Nem sikerült lekérni Az adatok által hivatkozott kereszthivatkozás utolsó próbálkozáskor 2024-01-25 11:53:22: Nem sikerült lekérni a 10.22331/q-2024-01-25-1234 hivatkozás által hivatkozott adatokat a Crossref-től. Ez normális, ha a DOI-t nemrég regisztrálták.

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
PlatoData.Network Vertical Generative Ai. Erősítse meg magát. Hozzáférés itt.
PlatoAiStream. Web3 Intelligence. Felerősített tudás. Hozzáférés itt.
PlatoESG. Carbon, CleanTech, Energia, Környezet, Nap, Hulladékgazdálkodás. Hozzáférés itt.
PlatoHealth. Biotechnológiai és klinikai vizsgálatok intelligencia. Hozzáférés itt.
Forrás: https://quantum-journal.org/papers/q-2024-01-25-1234/

Időbélyeg: Január 25, 2024

Időbélyeg: 25. október 2023.

Az extrém kvantumosság ortonormális alapjai

Újra kiadta Platón

Absztrakt

Népszerű összefoglaló

► BibTeX adatok

► Referenciák

Idézi

Még több Quantum Journal

Csővezetékes korrelált minimális súly tökéletes illeszkedése a felületi kódhoz

Többkarú kvantumbanditák: Kutatás kontra kizsákmányolás a kvantumállapotok tulajdonságainak megismerésekor

A mérésen alapuló kvantumhuzal osztályozása PEPS stabilizátorban

Quantum Monte Carlo integráció: Teljes előny a minimális áramköri mélységben

Továbbfejlesztett DIQKD protokollok véges méretű elemzéssel

Emergens kvantumállapot-tervek és biunitaritás a kettős egységáramkörök dinamikájában

Elfogultságra szabott kvantum LDPC kódok

Pontos és hatékony Lanczos-módszer kvantumszámítógépen

Az oksági dinamika lokális interakciókat jelent?

A gravitációs kölcsönhatások kvantumtermészetének vizsgálatáról a kvantummechanika nemlineáris korrekcióinak jelenlétében

Rólunk

Vertical Search & Ai

Emelvény

Maradjon kapcsolatban

Fiók