Vitalik Buterin keresztül a Vitalik Buterin Blog
Ez a bejegyzés tükre a címen https://medium.com/@VitalikButerin/quadratic-aritmetic-programs-from-zero-to-hero-f6d558cea649
Az utóbbi időben nagy az érdeklődés a zk-SNARK mögötti technológia iránt, és az emberek egyre inkább próbálja demisztifikálni olyasvalami, amit sokan „holdmatematikának” hívnak a megfejthetetlen bonyolultsága miatt. A zk-SNARK-okat valóban elég nehéz megfogni, különösen a mozgó alkatrészek nagy száma miatt, amelyeknek össze kell állniuk ahhoz, hogy az egész működjön, de ha a technológiát darabonként bontjuk le, akkor a megértése egyszerűbbé válik.
Ennek a bejegyzésnek nem célja a zk-SNARK-ok teljes körű bemutatása; háttértudásként azt feltételezi, hogy (i) tudja, mik a zk-SNARK-ok és mit csinálnak, és (ii) elég matematikai ismeretekkel rendelkezik ahhoz, hogy képes legyen érvelni olyan dolgokról, mint a polinomok (ha a �(�)+�(�) =(�+�)(�) , ahol � és � polinomok, természetesnek és magától értetődőnek tűnik az Ön számára, akkor a megfelelő szinten van). Inkább a bejegyzés mélyebbre ás a technológia mögött meghúzódó gépezetben, és megpróbálja a lehető legjobban elmagyarázni a csővezeték első felét, ahogyan a zk-SNARK kutatója, Eran Tromer itt rajzolta meg:

A lépések itt két részre bonthatók. Először is, a zk-SNARK-ok nem alkalmazhatók közvetlenül semmilyen számítási problémára; hanem a problémát a megfelelő „formába” kell alakítani ahhoz, hogy a probléma működjön. Az űrlapot „kvadratikus aritmetikai programnak” (QAP) nevezik, és egy függvény kódjának átalakítása ezek egyikévé maga nagyon nem triviális. A függvény kódjának QAP-vé való konvertálásának folyamata mellett egy másik folyamat is futtatható, így ha van bemenete a kódhoz, létrehozhat egy megfelelő megoldást (amit néha a QAP „tanújának” neveznek). Ezek után van egy másik meglehetősen bonyolult folyamat a tényleges „nulla tudású bizonyíték” létrehozására ennek a tanúnak, és egy külön eljárás annak a bizonyítéknak az ellenőrzésére, hogy valaki más átadta neked, de ezek olyan részletek, amelyek nem tartoznak ehhez a bejegyzéshez. .
A választott példa egy egyszerű: bizonyítja, hogy ismeri a köbös egyenlet megoldását: �3+�+5=35 (tipp: a válasz 3). Ez a probléma elég egyszerű ahhoz, hogy az eredményül kapott QAP ne legyen olyan nagy, hogy megfélemlítsen, de elég nem triviális ahhoz, hogy láthassa az összes gépezet működését.
Írjuk fel a függvényünket a következőképpen:
def qeval(x):
y = x**3
return x + y + 5Az itt használt egyszerű speciális célú programozási nyelv támogatja az alapvető aritmetikát (+, −, ⋅, /), az állandó hatványozást (�7, de nem ��) és a változók hozzárendelését, ami elég erős ahhoz, hogy elméletileg meg tudja csinálni. a benne lévő bármilyen számítás (amíg a számítási lépések száma korlátos; hurkok nem megengedettek). Vegye figyelembe, hogy a modulo (%) és az összehasonlító operátorok (<, >, ≤, ≥) NEM támogatottak, mivel nincs hatékony módja a modulo vagy az összehasonlításnak közvetlenül véges ciklikus csoportos aritmetikában (legyen hálás ezért, ha volt rá mód) Ha bármelyiket megteszi, akkor az elliptikus görbe kriptográfia gyorsabban törne, mint ahogy azt mondaná: „bináris keresés” és „kínai maradéktétel”).
A nyelvet kiterjesztheti a modulóra és az összehasonlításokra, ha segédbemenetként bitdekompozíciókat (pl. 13=23+22+1) ad meg, bizonyítja ezeknek a felbontásoknak a helyességét, és bináris áramkörökben számol; véges mezős aritmetikában az egyenlőség (==) ellenőrzése is kivitelezhető, sőt egy kicsit egyszerűbb is, de ezekre a részletekre most nem térünk ki. A nyelvet kiterjeszthetjük a feltételes feltételek támogatására (pl. ha �<5:�=7; else: �=9), ha aritmetikai formává alakítjuk őket: �=7⋅(�<5)+9⋅(�≥5 ), de vegye figyelembe, hogy a feltételes feltétel mindkét „útvonalát” végre kell hajtani, és ha sok beágyazott feltétele van, akkor ez nagy mennyiségű többletköltséggel járhat.
Most menjünk végig ezen a folyamaton lépésről lépésre. Ha ezt maga szeretné megtenni bármely kódrészlethez, akkor én itt implementált egy fordítót (Csak oktatási célokra; még nem áll készen QAP-ok készítésére a valós zk-SNARK-okhoz!).
elhalványulás
Az első lépés egy „kiegyenlítő” eljárás, ahol az eredeti kódot, amely tetszőlegesen összetett utasításokat és kifejezéseket tartalmazhat, kétféle utasítássorozattá alakítjuk át: �=� (ahol � lehet változó vagy szám ) és �=� (��) � (ahol a �� lehet +, −, ⋅, / és a � és � lehetnek változók, számok vagy önmagukban is részkifejezések). Ezeket az állításokat úgy képzelheti el, mint egy áramkör logikai kapuját. A fenti kód simítási folyamatának eredménye a következő:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5Ha elolvassa az eredeti kódot és a kódot itt, akkor meglehetősen könnyen láthatja, hogy a kettő egyenértékű.
Kapuk az R1CS-hez
Most ezt átalakítjuk egy úgynevezett rang-1 kényszerrendszerré (R1CS). Egy R1CS három vektorból álló csoportok sorozata (�, �, �), és egy R1CS megoldása egy � vektor, ahol �-nek teljesítenie kell a �.�⋅�.�−�.�=0 egyenletet, ahol . a pontszorzatot képviseli – egyszerűbben, ha „összehúzzuk” a � és a �-t, megszorozva a két értéket ugyanabban a pozícióban, majd felvesszük ezeknek a szorzatoknak az összegét, majd ugyanezt tesszük � és �, majd � és � , akkor a harmadik eredmény megegyezik az első két eredmény szorzatával. Például ez egy elégedett R1CS:
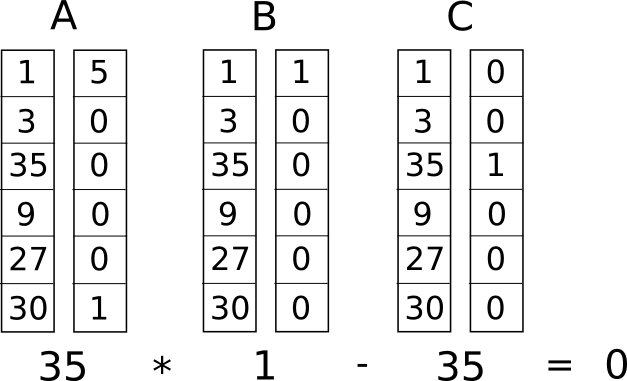
De ahelyett, hogy csak egy megkötésünk lenne, sok megszorításunk lesz: minden logikai kapuhoz egy. Van egy szabványos módszer a logikai kapu (�,�,�) hármassá alakítására, attól függően, hogy mi a művelet (+, −, ⋅ vagy /), és hogy az argumentumok változók vagy számok. Az egyes vektorok hossza megegyezik a rendszerben lévő változók teljes számával, beleértve az 1-es számot képviselő első indexnél egy álváltozót, a bemeneti változókat, a kimenetet képviselő ~out álváltozót, majd az összes köztes változók (���1 és ���2 fent); A vektorok általában nagyon ritkák, csak azokat a réseket töltik ki, amelyek megfelelnek azoknak a változóknak, amelyeket valamilyen logikai kapu érint.
Először is megadjuk a változóleképezést, amelyet használni fogunk:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'A megoldásvektor az összes változóhoz tartozó hozzárendeléseket tartalmazza, ebben a sorrendben.
Most a (�,�,�) hármast adjuk az első kapuhoz:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Látható, hogy ha a megoldásvektor a második pozícióban 3-at, a negyedik pozícióban pedig 9-et tartalmaz, akkor a megoldásvektor többi tartalmától függetlenül a pontszorzat-ellenőrzés 3⋅3=9-re csapódik le, és szóval el fog múlni. Ha a megoldásvektor második pozíciójában −3, a negyedik helyen pedig 9 van, akkor az ellenőrzés is sikeres lesz; Valójában, ha a megoldásvektor 7 a második pozícióban és 49 a negyedik pozícióban, akkor ez az ellenőrzés továbbra is megfelel - ennek az első ellenőrzésnek az a célja, hogy ellenőrizze az első kapu be- és kimeneteinek konzisztenciáját.
Most pedig menjünk a második kapuhoz:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]Az első pontos termékellenőrzéshez hasonló stílusban itt ellenőrizzük, hogy ���1⋅�=�.
Most a harmadik kapu:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]Itt a minta némileg eltér: a megoldásvektor első elemét megszorozzuk a második elemmel, majd az ötödik elemmel, összeadjuk a két eredményt, és ellenőrizzük, hogy az összeg megegyezik-e a hatodik elemmel. Mivel a megoldásvektor első eleme mindig egy, ez csak egy összeadás-ellenőrzés, annak ellenőrzése, hogy a kimenet megegyezik-e a két bemenet összegével.
Végül a negyedik kapu:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]Itt az utolsó csekket értékeljük, ~out =���2+5. A pontszorzat-ellenőrzés úgy működik, hogy a megoldásvektorban a hatodik elemet veszi, ötször hozzáadja az első elemet (emlékeztető: az első elem 1, tehát ez gyakorlatilag 5 hozzáadását jelenti), és összeveti a harmadik elemmel, ahol tárolja a kimeneti változót.
És ott van az R1CS-ünk négy megkötéssel. A tanú egyszerűen az összes változóhoz való hozzárendelés, beleértve a bemeneti, kimeneti és belső változókat is:
[1, 3, 35, 9, 27, 30]Ezt kiszámolhatja úgy, hogy egyszerűen „végrehajtja” a fenti összelapított kódot, a �=3 bemeneti változó-hozzárendeléssel kezdve, és számítás közben megadja az összes köztes változó értékét és a kimenetet.
A teljes R1CS összerakva:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]R1CS - QAP
A következő lépés ennek az R1CS-nek az átalakítása QAP formává, amely pontosan ugyanazt a logikát valósítja meg, kivéve a polinomokat a pontszorzatok helyett. Ezt a következőképpen tesszük. Négy három, hat hosszúságú vektorból álló csoportból megyünk hat három 3 fokos polinomból álló csoportba, ahol az egyes polinomokat értékeljük. x koordináta az egyik korlátot jelenti. Vagyis ha a polinomokat �=1-re értékeljük, akkor megkapjuk az első vektorhalmazunkat, ha a polinomokat �=2-re értékeljük, akkor megkapjuk a második vektorkészletünket, és így tovább.
Ezt az átalakítást az úgynevezett a segítségével végezhetjük el Lagrange interpoláció. A probléma, amelyet a Lagrange-interpoláció megold, a következő: ha van egy ponthalmaza (azaz (�,�) koordinátapár), akkor ezeken a pontokon Lagrange-interpolációval egy polinomot kapunk, amely áthalad ezeken a pontokon. Ezt úgy tesszük, hogy felbontjuk a feladatot: minden � koordinátához létrehozunk egy polinomot, amelynek a kívánt koordinátája az adott koordinátán, és 0 koordinátája az összes többi, minket érdeklő koordinátán, majd megkapjuk a végső értéket. eredményként összeadjuk az összes polinomot.
Vegyünk egy példát. Tegyük fel, hogy olyan polinomot akarunk, amely átmegy (1,3),(2,2) és (3,4)-en. Kezdjük egy polinom létrehozásával, amely átmegy (1,3), (2,0) és (3,0). Mint kiderült, könnyű olyan polinomot készíteni, amely �=1-nél „kilóg”, a többi érdekes pontnál pedig nulla; egyszerűen csináljuk:
(x - 2) * (x - 3)Ami így néz ki:
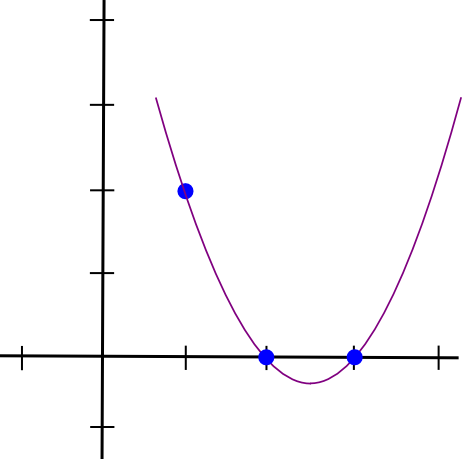
Most már csak „át kell méretezni”, hogy az x=1 magasság megfelelő legyen:
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))Ez megadja nekünk:
1.5 * x**2 - 7.5 * x + 9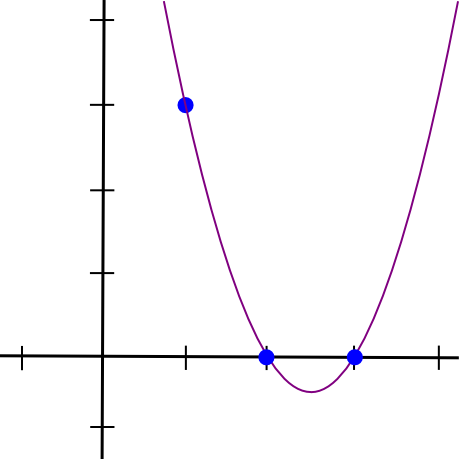
Ezután ugyanezt tesszük a másik két ponttal, és két másik hasonlónak tűnő polinomot kapunk, azzal a különbséggel, hogy �=2 és �=3 értéknél „kilógnak” �=1 helyett. Összeadjuk a hármat, és így kapjuk:
1.5 * x**2 - 5.5 * x + 7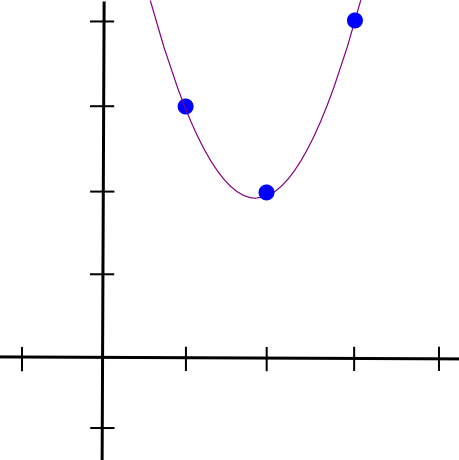
Pontosan a kívánt koordinátákkal. A fent leírt algoritmus �(�3) időt vesz igénybe, mivel � pont van, és minden ponthoz �(�2) idő szükséges a polinomok összeszorzásához; egy kis gondolkodással ez �(�2) időre csökkenthető, és sokkal több gondolkodással, gyors Fourier-transzformációs algoritmusok és hasonlók használatával még tovább csökkenthető – ez a kulcsfontosságú optimalizálás, amikor a zk-ben megszokott függvények -A SNARK-oknak a gyakorlatban gyakran sok ezer kapujuk van.
Most használjuk a Lagrange interpolációt az R1CS átalakításához. Azt fogjuk tenni, hogy minden � vektorból kivesszük az első értéket, majd Lagrange-interpolációval polinomot készítünk belőle (ahol a polinom �-ben való kiértékelésével megkapjuk a �-ik vektor első értékét), ismételjük meg a folyamatot. minden � és � vektor első értékéhez, majd ismételje meg ezt a folyamatot a második értékeknél, a harmadiknál, értékeknél és így tovább. A kényelem kedvéért most megadom a válaszokat:
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]Az együtthatók növekvő sorrendben vannak, tehát a fenti első polinom valójában 0.833⋅�3—5⋅�2+9.166⋅�−5. Ez a polinomhalmaz (plusz egy Z polinom, amelyet később elmagyarázok) alkotja a paramétereket ehhez a QAP-példányhoz. Ne feledje, hogy az idáig tartó összes munkát csak egyszer kell elvégezni minden olyan függvénynél, amelyet a zk-SNARK használatával próbál ellenőrizni; a QAP paraméterek generálása után újra felhasználhatók.
Próbáljuk kiértékelni ezeket a polinomokat �=1-nél. Egy polinom értékelése �=1-nél egyszerűen azt jelenti, hogy összeadjuk az összes együtthatót (minthogy 1�=1 minden � esetén), tehát nem nehéz. Kapunk:
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0És lám, amit itt kapunk, az pontosan ugyanaz, mint a fent létrehozott első logikai kapu három vektorának halmaza.
A QAP ellenőrzése
Most mi értelme ennek az őrült átalakulásnak? A válasz az, hogy ahelyett, hogy az R1CS-ben külön-külön ellenőriznénk a megszorításokat, most ellenőrizhetjük az összes megkötést egyszerre pontszerű termékellenőrzés elvégzésével a polinomokon.
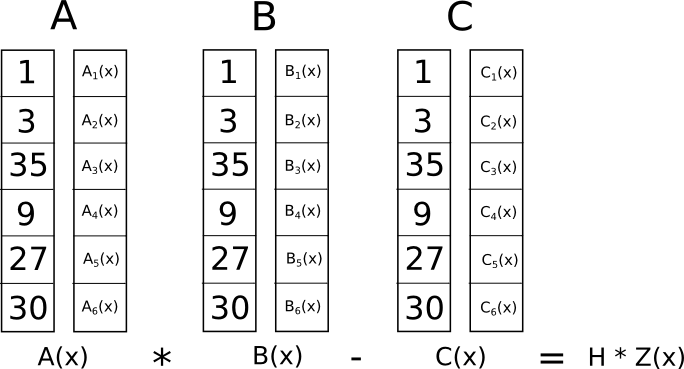
Mivel ebben az esetben a pontszorzat-ellenőrzés polinomok összeadásának és szorzásának sorozata, az eredmény maga egy polinom lesz. Ha az eredményül kapott polinom minden � koordinátán kiértékelve, amelyet fentebb egy logikai kapu ábrázolására használtunk, egyenlő nullával, akkor ez azt jelenti, hogy az összes ellenőrzés sikeres; ha a kapott polinom a logikai kaput reprezentáló � koordináták legalább egyikén kiértékelve nullától eltérő értéket ad, akkor ez azt jelenti, hogy a logikai kapuba bemenő és onnan kilépő értékek inkonzisztensek (azaz a kapu �=�⋅�� �1, de a megadott értékek lehetnek �=2,���1=2 és �=5).
Vegye figyelembe, hogy a kapott polinomnak magának nem kell nullának lennie, és a legtöbb esetben nem is lesz az; bármilyen viselkedése lehet azokon a pontokon, amelyek nem felelnek meg egyetlen logikai kapunak sem, mindaddig, amíg az eredmény nulla az összes pontban, do valamilyen kapunak felel meg. A helyesség ellenőrzése érdekében valójában nem értékeljük ki a �=�.�⋅�.�−�.� polinomot minden kapunak megfelelő pontban; ehelyett osztjuk � egy másik polinommal, �, és ellenőrizzük, hogy � egyenletesen oszt-e � – vagyis az �/� osztás nem hagy maradékot.
A � meghatározása: (�−1)⋅(�−2)⋅(�−3)… – a legegyszerűbb polinom, amely minden logikai kapunak megfelelő pontban egyenlő nullával. Az algebra elemi ténye, hogy bármilyen az összes pontban nullával egyenlő polinomnak ennek a minimális polinomnak a többszörösének kell lennie, és ha egy polinom többszöröse �, akkor bármelyik pontban a kiértékelése nulla lesz; ez az egyenértékűség sokkal könnyebbé teszi a dolgunkat.
Most végezzük el a pontszorzat-ellenőrzést a fenti polinomokkal. Először is a köztes polinomok:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]Most �.�⋅�.�—�.�:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Most a �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4) minimális polinom:
Z = [24, -50, 35, -10, 1]És ha a fenti eredményt elosztjuk �-vel, akkor kapjuk:
h = t / Z = [-3.666, 17.055, -3.444]Maradék nélkül.
Így megvan a megoldás a QAP-ra. Ha megpróbáljuk meghamisítani az R1CS megoldás bármely változóját, amelyből ezt a QAP-megoldást származtatjuk – mondjuk az utolsót állítsuk 31-re 30 helyett, akkor egy � polinomot kapunk, amely az egyik ellenőrzésen sikertelen (az adott esetben ebben az esetben a �=3-nál kapott eredmény 1 helyett −0), továbbá � nem lenne � többszöröse; �/� elosztása inkább [−5.0,8.833,−4.5,0.666] maradékot adna.
Vegye figyelembe, hogy a fenti egyszerűsítés; „a való világban” az összeadás, szorzás, kivonás és osztás nem szabályos számokkal, hanem véges mezőelemekkel fog megtörténni – ez egy kísérteties fajta aritmetika, amely önkonzisztens, tehát az összes általunk ismert és kedvelt algebrai törvény továbbra is igaz, de ahol minden válasz valamilyen véges méretű halmaz eleme, általában 0 és �−1 közötti egész számok bizonyos � esetén. Például, ha �=13, akkor 1/2=7 (és 7⋅2=1), 3⋅5=2 és így tovább. A végesmezős aritmetika használata megszünteti a kerekítési hibák miatti aggódást, és lehetővé teszi, hogy a rendszer szépen működjön az elliptikus görbékkel, amelyek végül szükségesek a zk-SNARK gépezet többi részéhez, amely a zk-SNARK protokollt valóban biztonságossá teszi.
Külön köszönet Eran Tromernek, hogy segített elmagyarázni nekem a zk-SNARK belső működésének sok részletét.
- SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
- PlatoData.Network Vertical Generative Ai. Erősítse meg magát. Hozzáférés itt.
- PlatoAiStream. Web3 Intelligence. Felerősített tudás. Hozzáférés itt.
- PlatoESG. Carbon, CleanTech, Energia, Környezet, Nap, Hulladékgazdálkodás. Hozzáférés itt.
- PlatoHealth. Biotechnológiai és klinikai vizsgálatok intelligencia. Hozzáférés itt.
- BlockOffsets. A környezetvédelmi ellentételezési tulajdon korszerűsítése. Hozzáférés itt.
- Forrás: Platón adatintelligencia.
