[मिरर] द्विघात अंकगणितीय कार्यक्रम: शून्य से नायक तक

विटालिक ब्यूटिरिन के माध्यम से विटालिक ब्यूटिरिन ब्लॉग

यह इस पोस्ट का दर्पण है https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

हाल ही में zk-SNARKs के पीछे की तकनीक में बहुत रुचि बढ़ी है और लोगों की रुचि बढ़ रही है रहस्य को उजागर करने की कोशिश कर रहा हूँ कुछ ऐसा जिसे कई लोग इसकी कथित अनिर्वचनीय जटिलता के कारण "चंद्र गणित" कहने लगे हैं। zk-SNARKs को समझना वास्तव में काफी चुनौतीपूर्ण है, विशेष रूप से चलने वाले हिस्सों की भारी संख्या के कारण जिन्हें पूरी चीज़ को काम करने के लिए एक साथ आने की आवश्यकता होती है, लेकिन अगर हम तकनीक को टुकड़े-टुकड़े करके तोड़ते हैं तो इसे समझना आसान हो जाता है।

इस पोस्ट का उद्देश्य zk-SNARKs का पूर्ण परिचय देना नहीं है; यह पृष्ठभूमि ज्ञान के रूप में मानता है कि (i) आप जानते हैं कि zk-SNARK क्या हैं और वे क्या करते हैं, और (ii) बहुपद जैसी चीजों के बारे में तर्क करने में सक्षम होने के लिए पर्याप्त गणित जानते हैं (यदि कथन �(�)+�(�) =(�+�)(�) , जहां � और � बहुपद हैं, आपको स्वाभाविक और स्पष्ट लगता है, तो आप सही स्तर पर हैं)। बल्कि, पोस्ट प्रौद्योगिकी के पीछे की मशीनरी में गहराई से उतरती है, और पाइपलाइन के पहले भाग को यथासंभव समझाने की कोशिश करती है, जैसा कि यहां zk-SNARK शोधकर्ता एरन ट्रोमर द्वारा तैयार किया गया है:

यहां की सीढ़ियों को दो हिस्सों में तोड़ा जा सकता है। सबसे पहले, zk-SNARKs को किसी भी कम्प्यूटेशनल समस्या पर सीधे लागू नहीं किया जा सकता है; बल्कि, समस्या को संचालित करने के लिए आपको समस्या को सही "रूप" में बदलना होगा। फॉर्म को "द्विघात अंकगणित कार्यक्रम" (क्यूएपी) कहा जाता है, और किसी फ़ंक्शन के कोड को इनमें से किसी एक में बदलना स्वयं अत्यधिक गैर-तुच्छ है। किसी फ़ंक्शन के कोड को QAP में परिवर्तित करने की प्रक्रिया के साथ-साथ एक और प्रक्रिया है जिसे साथ में चलाया जा सकता है ताकि यदि आपके पास कोड में इनपुट हो तो आप एक संबंधित समाधान बना सकें (कभी-कभी इसे QAP का "साक्षी" भी कहा जाता है)। इसके बाद, इस गवाह के लिए वास्तविक "शून्य ज्ञान प्रमाण" बनाने के लिए एक और काफी जटिल प्रक्रिया है, और इस सबूत को सत्यापित करने के लिए एक अलग प्रक्रिया है कि कोई और आपके पास जाता है, लेकिन ये विवरण हैं जो इस पोस्ट के दायरे से बाहर हैं .

हम जो उदाहरण चुनेंगे वह सरल है: यह साबित करना कि आप घन समीकरण का हल जानते हैं: �3+�+5=35 (संकेत: उत्तर 3 है)। यह समस्या इतनी सरल है कि परिणामी QAP इतना बड़ा नहीं होगा कि डराने वाला हो, लेकिन इतना गैर-तुच्छ होगा कि आप देख सकते हैं कि सभी मशीनरी काम में आ रही हैं।

आइए हम अपना कार्य इस प्रकार लिखें:

def qeval(x):
    y = x**3
    return x + y + 5

जिस सरल विशेष प्रयोजन प्रोग्रामिंग भाषा का हम यहां उपयोग कर रहे हैं वह बुनियादी अंकगणित (+, -, ⋅, /), निरंतर-शक्ति घातांक (�7 लेकिन �� नहीं) और परिवर्तनीय असाइनमेंट का समर्थन करती है, जो इतनी शक्तिशाली है कि आप सैद्धांतिक रूप से ऐसा कर सकते हैं इसके अंदर कोई भी गणना (जब तक कम्प्यूटेशनल चरणों की संख्या सीमित है; लूप की अनुमति नहीं है)। ध्यान दें कि मॉड्यूलो (%) और तुलना ऑपरेटर (<, >, ≤, ≥) समर्थित नहीं हैं, क्योंकि परिमित चक्रीय समूह अंकगणित में सीधे मॉड्यूलो या तुलना करने का कोई कुशल तरीका नहीं है (इसके लिए आभारी रहें; अगर कोई रास्ता था इनमें से किसी एक को करने के लिए, तो अण्डाकार वक्र क्रिप्टोग्राफी आपके "बाइनरी सर्च" और "चीनी शेष प्रमेय") की तुलना में तेजी से टूट जाएगी।

आप सहायक इनपुट के रूप में बिट डीकंपोजिशन (उदाहरण के लिए 13=23+22+1) प्रदान करके, उन डीकंपोजिशन की शुद्धता साबित करने और बाइनरी सर्किट में गणित करके भाषा को मॉड्यूलो और तुलनाओं तक बढ़ा सकते हैं; परिमित क्षेत्र अंकगणित में, समानता (==) जांच करना भी संभव है और वास्तव में थोड़ा आसान है, लेकिन ये दोनों विवरण हैं जिन पर हम अभी चर्चा नहीं करेंगे। हम सशर्तों का समर्थन करने के लिए भाषा का विस्तार कर सकते हैं (उदाहरण के लिए यदि �<5:�=7; अन्यथा: �=9) को अंकगणितीय रूप में परिवर्तित करके: �=7⋅(�<5)+9⋅(�≥5) ) हालांकि ध्यान दें कि कंडीशनल के दोनों "पथों" को निष्पादित करने की आवश्यकता होगी, और यदि आपके पास कई नेस्टेड कंडीशनल हैं तो इससे बड़ी मात्रा में ओवरहेड हो सकता है।

आइए अब इस प्रक्रिया को चरण दर चरण समझते हैं। यदि आप कोड के किसी भाग के लिए इसे स्वयं करना चाहते हैं, तो I यहां एक कंपाइलर लागू किया गया (केवल शैक्षणिक उद्देश्यों के लिए; वास्तविक दुनिया के zk-SNARKs के लिए QAPs बनाने के लिए अभी तक तैयार नहीं है!)।

सपाट

पहला चरण एक "फ़्लैटनिंग" प्रक्रिया है, जहाँ हम मूल कोड को, जिसमें मनमाने ढंग से जटिल कथन और अभिव्यक्तियाँ हो सकती हैं, कथनों के एक अनुक्रम में परिवर्तित करते हैं जो दो रूपों में होते हैं: �=� (जहाँ � एक चर या एक संख्या हो सकता है) ) और �=� (��) � (जहां �� +, −, ⋅, / और � हो सकता है और � चर, संख्याएं या स्वयं उप-अभिव्यक्ति हो सकते हैं)। आप इनमें से प्रत्येक कथन को एक सर्किट में लॉजिक गेट की तरह सोच सकते हैं। उपरोक्त कोड के लिए फ़्लैटनिंग प्रक्रिया का परिणाम इस प्रकार है:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

यदि आप मूल कोड और यहां कोड पढ़ते हैं, तो आप काफी आसानी से देख सकते हैं कि दोनों बराबर हैं।

R1CS के द्वार

अब, हम इसे रैंक-1 बाधा प्रणाली (R1CS) नामक चीज़ में परिवर्तित करते हैं। एक R1CS तीन वैक्टर (�, ​​�, �) के समूहों का एक क्रम है, और R1CS का समाधान एक वेक्टर � ​​है, जहां � को समीकरण �.�⋅�.�−�.�=0 को संतुष्ट करना होगा, जहां . डॉट उत्पाद का प्रतिनिधित्व करता है - सरल शब्दों में, यदि हम � और � को "एक साथ ज़िप करते हैं", दो मानों को एक ही स्थिति में गुणा करते हैं, और फिर इन उत्पादों का योग लेते हैं, फिर � और � के साथ भी ऐसा ही करते हैं और फिर � और � , तो तीसरा परिणाम पहले दो परिणामों के उत्पाद के बराबर होता है। उदाहरण के लिए, यह एक संतुष्ट R1CS है:

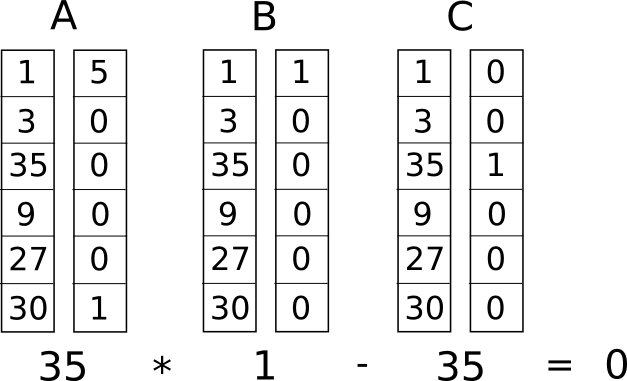
लेकिन केवल एक बाधा के बजाय, हमारे पास कई बाधाएं होंगी: प्रत्येक लॉजिक गेट के लिए एक। ऑपरेशन क्या है (+, −, ⋅ या /) और क्या तर्क चर या संख्या हैं, इसके आधार पर लॉजिक गेट को (�,�,�) ट्रिपल में परिवर्तित करने का एक मानक तरीका है। प्रत्येक वेक्टर की लंबाई सिस्टम में वेरिएबल्स की कुल संख्या के बराबर होती है, जिसमें एक डमी वेरिएबल ~पहले इंडेक्स पर एक नंबर 1 का प्रतिनिधित्व करता है, इनपुट वेरिएबल, एक डमी वेरिएबल ~आउटपुट का प्रतिनिधित्व करता है, और फिर सभी मध्यवर्ती चर (ऊपर ��1 और ��2); वेक्टर आम तौर पर बहुत विरल होते हैं, केवल वेरिएबल के अनुरूप स्लॉट भरते हैं जो कुछ विशेष लॉजिक गेट से प्रभावित होते हैं।

सबसे पहले, हम वेरिएबल मैपिंग प्रदान करेंगे जिसका हम उपयोग करेंगे:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

समाधान वेक्टर में इन सभी चरों के लिए उसी क्रम में असाइनमेंट शामिल होंगे।

अब, हम पहले गेट के लिए (�,�,�) ट्रिपल देंगे:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

आप देख सकते हैं कि यदि समाधान वेक्टर में दूसरे स्थान पर 3 और चौथे स्थान पर 9 है, तो समाधान वेक्टर की बाकी सामग्री की परवाह किए बिना, डॉट उत्पाद जांच 3⋅3=9 तक कम हो जाएगी, और तो यह बीत जाएगा. यदि समाधान वेक्टर में दूसरे स्थान पर -3 और चौथे स्थान पर 9 है, तो चेक भी पास हो जाएगा; वास्तव में, यदि समाधान वेक्टर में दूसरे स्थान पर 7 और चौथे स्थान पर 49 है तो वह चेक अभी भी पास हो जाएगा - इस पहले चेक का उद्देश्य केवल पहले गेट के इनपुट और आउटपुट की स्थिरता को सत्यापित करना है।

अब, चलिए दूसरे द्वार पर चलते हैं:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

पहले डॉट उत्पाद जांच के समान शैली में, यहां हम ���1⋅�=� की जांच कर रहे हैं।

अब, तीसरा द्वार:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

यहां, पैटर्न कुछ अलग है: यह समाधान वेक्टर में पहले तत्व को दूसरे तत्व से गुणा करता है, फिर पांचवें तत्व से, दो परिणामों को जोड़ता है, और जांच करता है कि योग छठे तत्व के बराबर है या नहीं। क्योंकि समाधान वेक्टर में पहला तत्व हमेशा एक होता है, यह सिर्फ एक अतिरिक्त जांच है, यह जांच कर कि आउटपुट दो इनपुट के योग के बराबर है।

अंत में, चौथा द्वार:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

यहां, हम अंतिम चेक का मूल्यांकन कर रहे हैं, ~आउट = ���2+5। डॉट उत्पाद जांच समाधान वेक्टर में छठा तत्व लेकर, पहले तत्व को पांच गुना जोड़कर काम करती है (अनुस्मारक: पहला तत्व 1 है, इसलिए इसका प्रभावी रूप से मतलब 5 जोड़ना है), और इसे तीसरे तत्व के खिलाफ जांचना है, जो कि हम कहां हैं आउटपुट वेरिएबल को स्टोर करें।

और वहां हमारे पास चार बाधाओं के साथ हमारा R1CS है। गवाह केवल इनपुट, आउटपुट और आंतरिक चर सहित सभी चर का असाइनमेंट है:

[1, 3, 35, 9, 27, 30]

आप ऊपर दिए गए चपटे कोड को बस "निष्पादित" करके, इनपुट वेरिएबल असाइनमेंट �=3 से शुरू करके, और सभी मध्यवर्ती वेरिएबल्स और आउटपुट के मूल्यों को डालकर उनकी गणना करके अपने लिए इसकी गणना कर सकते हैं।

पूरा R1CS एक साथ रखा गया है:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS से QAP

अगला कदम इस R1CS को लेना और इसे QAP फॉर्म में परिवर्तित करना है, जो डॉट उत्पादों के बजाय बहुपद का उपयोग करने के अलावा बिल्कुल उसी तर्क को लागू करता है। हम इसे इस प्रकार करते हैं। हम लंबाई के तीन सदिशों के चार समूहों से तीन डिग्री-3 बहुपदों के छह से छह समूहों तक जाते हैं, जहां प्रत्येक पर बहुपदों का मूल्यांकन किया जाता है। x समन्वय बाधाओं में से एक का प्रतिनिधित्व करता है। अर्थात्, यदि हम बहुपदों का मूल्यांकन �=1 पर करते हैं, तो हमें सदिशों का पहला सेट मिलता है, यदि हम बहुपदों का मूल्यांकन �=2 पर करते हैं, तो हमें सदिशों का दूसरा सेट मिलता है, इत्यादि।

हम यह परिवर्तन a नामक किसी चीज़ का उपयोग करके कर सकते हैं लैग्रेंज इंटरपोलेशन. लैग्रेंज इंटरपोलेशन द्वारा हल की जाने वाली समस्या यह है: यदि आपके पास बिंदुओं का एक सेट है (यानी (�,�) समन्वय जोड़े), तो उन बिंदुओं पर लैग्रेंज इंटरपोलेशन करने से आपको एक बहुपद मिलता है जो उन सभी बिंदुओं से होकर गुजरता है। हम समस्या को विघटित करके ऐसा करते हैं: प्रत्येक �निर्देशांक के लिए, हम एक बहुपद बनाते हैं जिसमें उस �निर्देशांक पर वांछित �निर्देशांक होता है और अन्य सभी �निर्देशांकों पर 0 का एक �निर्देशांक होता है, जिनमें हम रुचि रखते हैं, और फिर अंतिम प्राप्त करते हैं। परिणाम स्वरूप हम सभी बहुपदों को एक साथ जोड़ते हैं।

चलिए एक उदाहरण देखते हैं. मान लीजिए कि हम एक बहुपद चाहते हैं जो (1,3),(2,2) और (3,4) से होकर गुजरता है। हम एक बहुपद बनाकर शुरुआत करते हैं जो (1,3),(2,0) और (3,0) से होकर गुजरता है। जैसा कि यह पता चला है, एक बहुपद बनाना जो �=1 पर "चिपकता है" और रुचि के अन्य बिंदुओं पर शून्य है, आसान है; हम बस यह करते हैं:

(x - 2) * (x - 3)

जो इस तरह दिखता है:

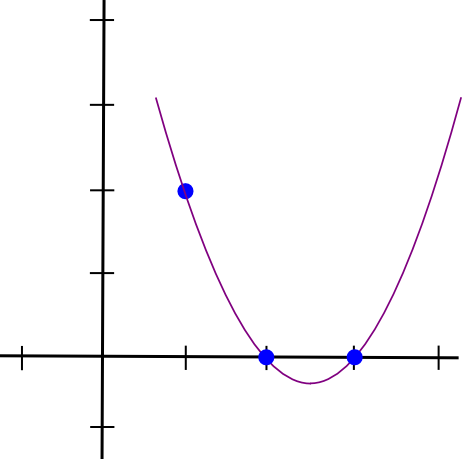
अब, हमें बस इसे "पुनर्विक्रय" करने की आवश्यकता है ताकि x=1 पर ऊंचाई सही हो:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

यह हमें देता है:

1.5 * x**2 - 7.5 * x + 9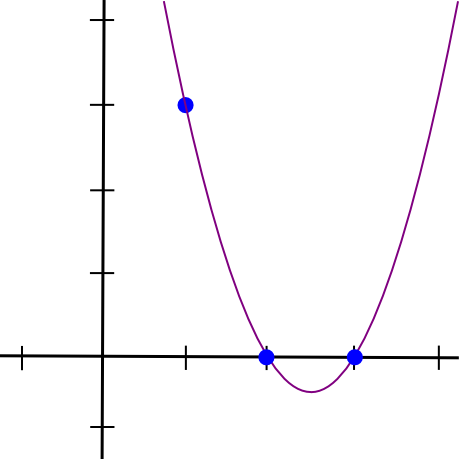

फिर हम अन्य दो बिंदुओं के साथ भी ऐसा ही करते हैं, और दो अन्य समान दिखने वाले बहुपद प्राप्त करते हैं, सिवाय इसके कि वे �=2 के बजाय �=3 और �=1 पर "चिपके" रहते हैं। हम तीनों को एक साथ जोड़ते हैं और प्राप्त करते हैं:

1.5 * x**2 - 5.5 * x + 7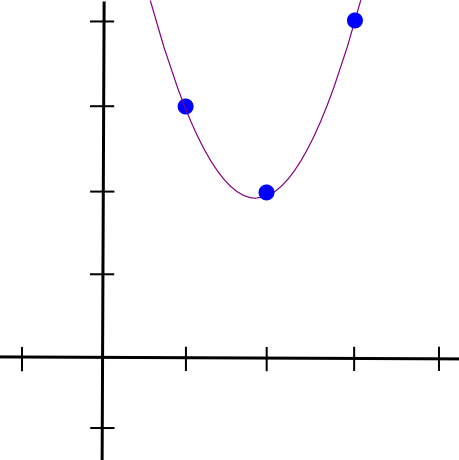

ठीक उसी निर्देशांक के साथ जो हम चाहते हैं। ऊपर वर्णित एल्गोरिथ्म में �(�3) समय लगता है, क्योंकि � बिंदु हैं और प्रत्येक बिंदु को बहुपदों को एक साथ गुणा करने के लिए �(�2) समय की आवश्यकता होती है; थोड़ी सी सोच के साथ, इसे �(�2) समय तक कम किया जा सकता है, और बहुत अधिक सोच के साथ, तेज फूरियर ट्रांसफॉर्म एल्गोरिदम और इसी तरह का उपयोग करके, इसे और भी कम किया जा सकता है - एक महत्वपूर्ण अनुकूलन जब फ़ंक्शन जो zk में उपयोग किए जाते हैं -व्यवहार में SNARKs में अक्सर कई हजारों द्वार होते हैं।

अब, आइए अपने R1CS को बदलने के लिए लैग्रेंज इंटरपोलेशन का उपयोग करें। हम जो करने जा रहे हैं वह प्रत्येक � वेक्टर से पहला मान लेना है, उसमें से एक बहुपद बनाने के लिए लैग्रेंज इंटरपोलेशन का उपयोग करना है (जहां � पर बहुपद का मूल्यांकन करने पर आपको �वें वेक्टर का पहला मान मिलता है), प्रक्रिया को दोहराएं प्रत्येक � और � वेक्टर के पहले मान के लिए, और फिर उस प्रक्रिया को दूसरे मान, तीसरे, मान, इत्यादि के लिए दोहराएं। सुविधा के लिए मैं अभी उत्तर प्रदान करूंगा:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

गुणांक आरोही क्रम में हैं, इसलिए उपरोक्त पहला बहुपद वास्तव में 0.833⋅⋅3—5⋅⋅2+9.166⋅−5 है। बहुपदों का यह सेट (प्लस एक Z बहुपद जिसे मैं बाद में समझाऊंगा) इस विशेष QAP उदाहरण के लिए पैरामीटर बनाता है। ध्यान दें कि इस बिंदु तक सभी कार्य प्रत्येक फ़ंक्शन के लिए केवल एक बार किए जाने की आवश्यकता है जिसे आप सत्यापित करने के लिए zk-SNARKs का उपयोग करने का प्रयास कर रहे हैं; एक बार QAP पैरामीटर तैयार हो जाने के बाद, उनका पुन: उपयोग किया जा सकता है।

आइए इन सभी बहुपदों का �=1 पर मूल्यांकन करने का प्रयास करें। �=1 पर एक बहुपद का मूल्यांकन करने का सीधा सा अर्थ है सभी गुणांकों को जोड़ना (जैसे सभी � के लिए 1�=1), इसलिए यह मुश्किल नहीं है। हम पाते हैं:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

और देखो, हमारे पास यहां जो कुछ है वह बिल्कुल पहले लॉजिक गेट के लिए तीन वैक्टर के सेट के समान है जो हमने ऊपर बनाया था।

QAP की जाँच हो रही है

अब इस पागलपन भरे बदलाव का क्या मतलब है? इसका उत्तर यह है कि R1CS में बाधाओं की व्यक्तिगत रूप से जाँच करने के बजाय, अब हम जाँच कर सकते हैं एक ही समय में सभी बाधाएँ डॉट उत्पाद जांच करके बहुपदों पर.

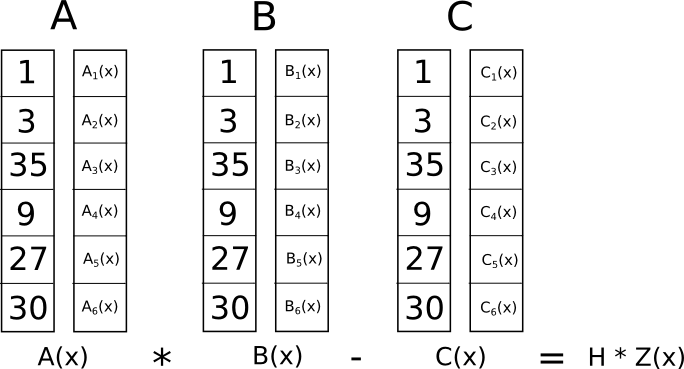
चूँकि इस मामले में डॉट उत्पाद जाँच बहुपदों के जोड़ और गुणन की एक श्रृंखला है, परिणाम स्वयं एक बहुपद होने वाला है। यदि परिणामी बहुपद, प्रत्येक � समन्वय पर मूल्यांकन किया जाता है जिसे हमने ऊपर एक तर्क गेट का प्रतिनिधित्व करने के लिए उपयोग किया है, शून्य के बराबर है, तो इसका मतलब है कि सभी चेक पास हो गए हैं; यदि तर्क गेट का प्रतिनिधित्व करने वाले � समन्वय में से कम से कम एक पर परिणामी बहुपद का मूल्यांकन एक गैर-शून्य मान देता है, तो इसका मतलब है कि उस तर्क गेट से अंदर और बाहर जाने वाले मान असंगत हैं (यानी गेट �=�⋅�� है) �1 लेकिन प्रदत्त मान �=2, ��1=2 और �=5) हो सकते हैं।

ध्यान दें कि परिणामी बहुपद का स्वयं शून्य होना आवश्यक नहीं है, और वास्तव में अधिकांश मामलों में ऐसा नहीं होगा; यह उन बिंदुओं पर कोई भी व्यवहार कर सकता है जो किसी भी लॉजिक गेट के अनुरूप नहीं हैं, जब तक कि सभी बिंदुओं पर परिणाम शून्य हो do कुछ गेट के अनुरूप. शुद्धता की जांच करने के लिए, हम वास्तव में गेट के अनुरूप प्रत्येक बिंदु पर बहुपद �=�.�⋅�.�−�.� का मूल्यांकन नहीं करते हैं; इसके बजाय, हम � को किसी अन्य बहुपद, � से विभाजित करते हैं, और जांचते हैं कि � समान रूप से विभाजित होता है - यानी, विभाजन �/� कोई शेष नहीं छोड़ता है।

� को (�−1)⋅(�−2)⋅(�−3)... के रूप में परिभाषित किया गया है - सबसे सरल बहुपद जो तर्क द्वारों के अनुरूप सभी बिंदुओं पर शून्य के बराबर है। यह बीजगणित का एक प्राथमिक तथ्य है कि कोई जो बहुपद इन सभी बिंदुओं पर शून्य के बराबर है, उसे इस न्यूनतम बहुपद का गुणज होना चाहिए, और यदि कोई बहुपद � का गुणज है तो उनमें से किसी भी बिंदु पर इसका मूल्यांकन शून्य होगा; यह समानता हमारे काम को बहुत आसान बना देती है।

अब, आइए वास्तव में उपरोक्त बहुपदों के साथ बिंदु गुणनफल की जाँच करें। सबसे पहले, मध्यवर्ती बहुपद:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

अब, �.�⋅�.�—�.�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

अब, न्यूनतम बहुपद �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):

Z = [24, -50, 35, -10, 1]

और यदि हम उपरोक्त परिणाम को � से विभाजित करते हैं, तो हमें मिलता है:

h = t / Z = [-3.666, 17.055, -3.444]

बिना किसी शेष के.

और इसलिए हमारे पास QAP का समाधान है। यदि हम R1CS समाधान में किसी भी वेरिएबल को गलत साबित करने का प्रयास करते हैं जिससे हम यह QAP समाधान प्राप्त कर रहे हैं - मान लीजिए, अंतिम को 31 के बजाय 30 पर सेट करें, तो हमें एक बहुपद मिलता है जो चेक में से एक को विफल कर देता है (उस विशेष में) मामले में, �=3 पर परिणाम 1 के बजाय −0 के बराबर होगा), और इसके अलावा � � का गुणज नहीं होगा; बल्कि, �/� को विभाजित करने पर शेषफल [−5.0,8.833,−4.5,0.666] प्राप्त होगा।

ध्यान दें कि उपरोक्त एक सरलीकरण है; "वास्तविक दुनिया में", जोड़, गुणा, घटाव और विभाजन नियमित संख्याओं के साथ नहीं होगा, बल्कि परिमित क्षेत्र तत्वों के साथ होगा - एक डरावना प्रकार का अंकगणित जो आत्मनिर्भर है, इसलिए सभी बीजगणितीय कानून हम जानते हैं और अभी भी पसंद करते हैं सत्य है, लेकिन जहां सभी उत्तर किसी परिमित आकार के सेट के तत्व हैं, आमतौर पर कुछ के लिए 0 से −1 तक की सीमा के भीतर पूर्णांक होते हैं। उदाहरण के लिए, यदि �=13, तो 1/2=7 (और 7⋅2=1),3⋅5=2, इत्यादि। परिमित क्षेत्र अंकगणित का उपयोग करने से गोलाई त्रुटियों के बारे में चिंता करने की आवश्यकता दूर हो जाती है और सिस्टम को अण्डाकार वक्रों के साथ अच्छी तरह से काम करने की अनुमति मिलती है, जो अंततः zk-SNARK मशीनरी के बाकी हिस्सों के लिए आवश्यक होता है जो zk-SNARK प्रोटोकॉल को वास्तव में सुरक्षित बनाता है।

मुझे zk-SNARKs की आंतरिक कार्यप्रणाली के बारे में कई विवरण समझाने में मदद करने के लिए एरन ट्रोमर को विशेष धन्यवाद।

• एसईओ संचालित सामग्री और पीआर वितरण। आज ही प्रवर्धित हो जाओ।
• प्लेटोडेटा.नेटवर्क वर्टिकल जेनरेटिव एआई। स्वयं को शक्तिवान बनाएं। यहां पहुंचें।
• प्लेटोआईस्ट्रीम। Web3 इंटेलिजेंस। ज्ञान प्रवर्धित। यहां पहुंचें।
• प्लेटोईएसजी. कार्बन, क्लीनटेक, ऊर्जा, पर्यावरण, सौर, कचरा प्रबंधन। यहां पहुंचें।
• प्लेटोहेल्थ। बायोटेक और क्लिनिकल परीक्षण इंटेलिजेंस। यहां पहुंचें।
• BlockOffsets. पर्यावरणीय ऑफसेट स्वामित्व का आधुनिकीकरण। यहां पहुंचें।
• स्रोत: प्लेटो डेटा इंटेलिजेंस।