[Miroir] Programmes arithmétiques quadratiques : de zéro à héros

Vitalik Buterin via le Blog de Vitalik Buterin

Ceci est un miroir du message de https://medium.com/@VitalikButerin/programmes-arithmétiques-quadratiques-de-zéro-à-héros-f6d558cea649

Il y a eu beaucoup d'intérêt ces derniers temps pour la technologie derrière les zk-SNARK, et les gens sont de plus en plus intéressés. essayer de démystifier quelque chose que beaucoup en sont venus à appeler « les mathématiques lunaires » en raison de sa complexité perçue comme indéchiffrable. Les zk-SNARK sont en effet assez difficiles à comprendre, notamment en raison du grand nombre de pièces mobiles qui doivent s'assembler pour que l'ensemble fonctionne, mais si nous décomposons la technologie pièce par pièce, sa compréhension devient plus simple.

Le but de cet article n'est pas de servir d'introduction complète aux zk-SNARK ; cela suppose comme connaissances de base que (i) vous savez ce que sont les zk-SNARK et ce qu'ils font, et (ii) connaissez suffisamment les mathématiques pour pouvoir raisonner sur des choses comme les polynômes (si l'instruction �(�)+�(�) =(�+�)(�) , où � et � sont des polynômes, vous semble naturel et évident, alors vous êtes au bon niveau). Au lieu de cela, l'article approfondit la machinerie derrière la technologie et tente d'expliquer au mieux la première moitié du pipeline, comme le dessine ici le chercheur de zk-SNARK, Eran Tromer :

Les étapes ici peuvent être divisées en deux moitiés. Premièrement, les zk-SNARK ne peuvent être appliqués directement à aucun problème de calcul ; vous devez plutôt convertir le problème dans la bonne « forme » pour que le problème puisse fonctionner. Le formulaire est appelé « programme arithmétique quadratique » (QAP), et transformer le code d’une fonction en l’un de ceux-ci est en soi très simple. Parallèlement au processus de conversion du code d'une fonction en QAP, il existe un autre processus qui peut être exécuté parallèlement afin que si vous avez une entrée dans le code, vous puissiez créer une solution correspondante (parfois appelée « témoin » du QAP). Après cela, il existe un autre processus assez complexe pour créer la véritable « preuve de connaissance nulle » pour ce témoin, et un processus distinct pour vérifier une preuve que quelqu'un d'autre vous transmet, mais ce sont des détails qui sortent du cadre de cet article. .

L’exemple que nous allons choisir est simple : prouver que vous connaissez la solution d’une équation cubique : �3+�+5=35 (indice : la réponse est 3). Ce problème est suffisamment simple pour que le QAP qui en résulte ne soit pas assez important pour être intimidant, mais suffisamment non trivial pour que vous puissiez voir toutes les machines entrer en jeu.

Écrivons notre fonction comme suit :

def qeval(x):
    y = x**3
    return x + y + 5

Le simple langage de programmation spécial que nous utilisons ici prend en charge l'arithmétique de base (+, −, ⋅, /), l'exponentiation à puissance constante (�7 mais pas ��) et l'affectation de variables, ce qui est suffisamment puissant pour que vous puissiez théoriquement le faire. tout calcul à l'intérieur de celui-ci (tant que le nombre d'étapes de calcul est limité ; aucune boucle n'est autorisée). Notez que les opérateurs modulo (%) et de comparaison (<, >, ≤, ≥) ne sont PAS pris en charge, car il n'existe aucun moyen efficace d'effectuer un modulo ou une comparaison directement dans l'arithmétique des groupes cycliques finis (soyez reconnaissants pour cela ; s'il y avait un moyen pour faire l’un ou l’autre, alors la cryptographie à courbe elliptique serait brisée plus rapidement que vous ne pouvez dire « recherche binaire » et « théorème des restes chinois »).

Vous pouvez étendre le langage au modulo et aux comparaisons en fournissant des décompositions de bits (par exemple 13=23+22+1) comme entrées auxiliaires, en prouvant l'exactitude de ces décompositions et en effectuant les calculs dans les circuits binaires ; en arithmétique des champs finis, effectuer des vérifications d'égalité (==) est également réalisable et en fait un peu plus facile, mais ce sont deux détails que nous n'aborderons pas pour le moment. Nous pouvons étendre le langage pour prendre en charge les conditions (par exemple si �<5 :�=7 ; sinon : �=9) en les convertissant sous une forme arithmétique : �=7⋅(�<5)+9⋅(�≥5 ), notez cependant que les deux « chemins » du conditionnel devront être exécutés, et si vous avez de nombreux conditionnels imbriqués, cela peut entraîner une surcharge importante.

Passons maintenant à ce processus étape par étape. Si vous voulez le faire vous-même pour n'importe quel morceau de code, je implémenté un compilateur ici (à des fins éducatives uniquement ; pas encore prêt à créer des QAP pour les zk-SNARK du monde réel !).

Aplanissement

La première étape est une procédure « d'aplatissement », dans laquelle nous convertissons le code original, qui peut contenir des instructions et des expressions arbitrairement complexes, en une séquence d'instructions qui se présentent sous deux formes : �=� (où � peut être une variable ou un nombre ) et �=� (��) � (où �� peut être +, −, ⋅, / et � et � peuvent être des variables, des nombres ou eux-mêmes des sous-expressions). Vous pouvez considérer chacune de ces instructions comme étant un peu comme des portes logiques dans un circuit. Le résultat du processus d’aplatissement du code ci-dessus est le suivant :

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

Si vous lisez le code original et le code ici, vous pouvez assez facilement voir que les deux sont équivalents.

Portes vers R1CS

Maintenant, nous convertissons cela en quelque chose appelé un système de contraintes de rang 1 (R1CS). Un R1CS est une séquence de groupes de trois vecteurs (�, �, �), et la solution d'un R1CS est un vecteur �, où � doit satisfaire l'équation �.�⋅�.�−�.�=0, où . représente le produit scalaire – en termes plus simples, si nous « compressons ensemble » � et �, en multipliant les deux valeurs dans les mêmes positions, puis prenons la somme de ces produits, puis faisons de même pour � et � puis � et � , alors le troisième résultat est égal au produit des deux premiers résultats. Par exemple, voici un R1CS satisfait :

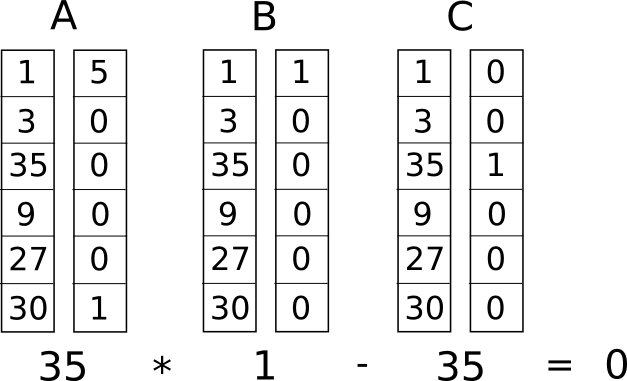
Mais au lieu d’avoir une seule contrainte, nous allons avoir plusieurs contraintes : une pour chaque porte logique. Il existe un moyen standard de convertir une porte logique en un triple (�,�,�) selon l'opération (+, −, ⋅ ou /) et si les arguments sont des variables ou des nombres. La longueur de chaque vecteur est égale au nombre total de variables dans le système, y compris une variable factice ~ une au premier index représentant le nombre 1, les variables d'entrée, une variable factice ~ out représentant la sortie, puis toutes les variables variables intermédiaires (����1 et ���2 ci-dessus) ; les vecteurs seront généralement très clairsemés, ne remplissant que les emplacements correspondant aux variables affectées par une porte logique particulière.

Tout d’abord, nous fournirons le mappage de variables que nous utiliserons :

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

Le vecteur solution sera constitué d’affectations pour toutes ces variables, dans cet ordre.

Maintenant, nous allons donner le triple (�,�,�) pour la première porte :

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

Vous pouvez voir que si le vecteur solution contient 3 en deuxième position et 9 en quatrième position, alors quel que soit le reste du contenu du vecteur solution, la vérification du produit scalaire se résumera à 3⋅3=9, et donc ça passera. Si le vecteur solution a −3 en deuxième position et 9 en quatrième position, le contrôle réussira également ; en fait, si le vecteur solution a 7 en deuxième position et 49 en quatrième position, alors cette vérification réussira quand même — le but de cette première vérification est de vérifier uniquement la cohérence des entrées et des sorties de la première porte.

Passons maintenant à la deuxième porte :

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

Dans un style similaire à la première vérification du produit scalaire, nous vérifions ici que ���1⋅�=�.

Maintenant, la troisième porte :

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

Ici, le modèle est quelque peu différent : il s'agit de multiplier le premier élément du vecteur solution par le deuxième élément, puis par le cinquième élément, d'ajouter les deux résultats et de vérifier si la somme est égale au sixième élément. Étant donné que le premier élément du vecteur solution est toujours un, il s'agit simplement d'une vérification d'addition, vérifiant que la sortie est égale à la somme des deux entrées.

Enfin, la quatrième porte :

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

Ici, nous évaluons la dernière vérification, ~out =���2+5. La vérification du produit scalaire fonctionne en prenant le sixième élément du vecteur de solution, en ajoutant cinq fois le premier élément (rappel : le premier élément est 1, cela signifie donc effectivement ajouter 5) et en le comparant au troisième élément, c'est là que nous stocker la variable de sortie.

Et voilà notre R1CS avec quatre contraintes. Le témoin est simplement l'affectation de toutes les variables, y compris les variables d'entrée, de sortie et internes :

[1, 3, 35, 9, 27, 30]

Vous pouvez calculer cela par vous-même en « exécutant » simplement le code aplati ci-dessus, en commençant par l'affectation de variable d'entrée �=3, et en insérant les valeurs de toutes les variables intermédiaires et la sortie au fur et à mesure que vous les calculez.

Le R1CS complet mis en place est :

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS vers QAP

L'étape suivante consiste à prendre ce R1CS et à le convertir sous forme QAP, qui implémente exactement la même logique, sauf en utilisant des polynômes au lieu de produits scalaires. Nous procédons comme suit. On passe de quatre groupes de trois vecteurs de longueur six à six groupes de trois polynômes de degré 3, où l'on évalue les polynômes à chaque coordonnée x représente une des contraintes. Autrement dit, si nous évaluons les polynômes à �=1, alors nous obtenons notre premier ensemble de vecteurs, si nous évaluons les polynômes à �=2, alors nous obtenons notre deuxième ensemble de vecteurs, et ainsi de suite.

Nous pouvons effectuer cette transformation en utilisant ce qu'on appelle un Interpolation de Lagrange. Le problème qu'une interpolation de Lagrange résout est le suivant : si vous avez un ensemble de points (c'est-à-dire des paires de coordonnées (�,�), alors faire une interpolation de Lagrange sur ces points vous donne un polynôme qui passe par tous ces points. Pour ce faire, nous décomposons le problème : pour chaque coordonnée �, nous créons un polynôme qui a la coordonnée � souhaitée à cette coordonnée � et une coordonnée � de 0 à toutes les autres coordonnées � qui nous intéressent, puis pour obtenir le résultat final résultat, nous additionnons tous les polynômes ensemble.

Faisons un exemple. Supposons que nous voulions un polynôme qui passe par (1,3), (2,2) et (3,4). On commence par faire un polynôme qui passe par (1,3), (2,0) et (3,0). Il s’avère qu’il est facile de créer un polynôme qui « dépasse » à �=1 et est nul aux autres points d’intérêt ; nous faisons simplement :

(x - 2) * (x - 3)

Qui ressemble à ceci :

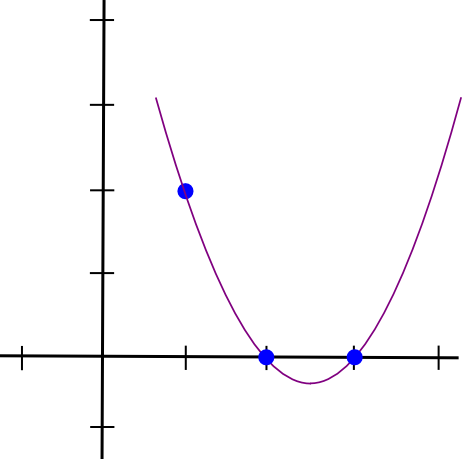
Il ne nous reste plus qu'à le "redimensionner" pour que la hauteur en x=1 soit correcte :

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

Cela nous donne:

1.5 * x**2 - 7.5 * x + 9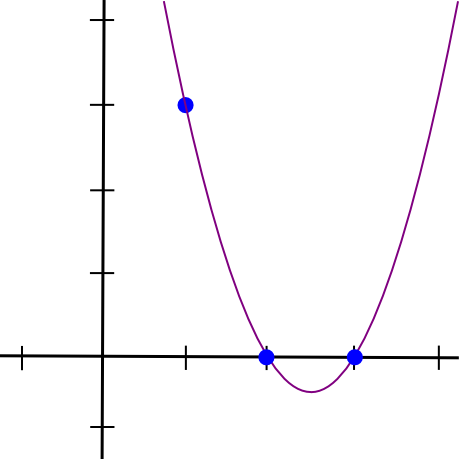

Nous faisons ensuite la même chose avec les deux autres points et obtenons deux autres polynômes d’apparence similaire, sauf qu’ils « ressortent » à �=2 et �=3 au lieu de �=1. On additionne les trois et on obtient :

1.5 * x**2 - 5.5 * x + 7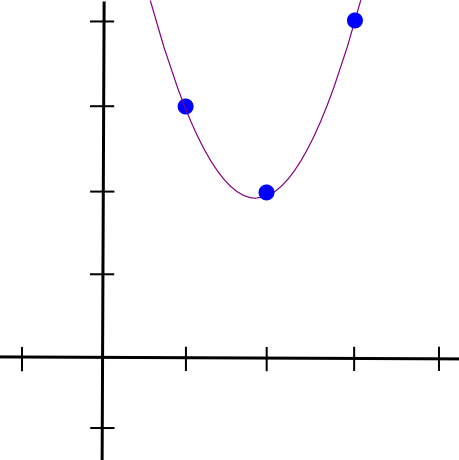

Avec exactement les coordonnées que nous voulons. L'algorithme tel que décrit ci-dessus prend �(�3) de temps, car il y a � points et chaque point nécessite �(�2) de temps pour multiplier les polynômes ensemble ; avec un peu de réflexion, cela peut être réduit à �(�2) temps, et avec beaucoup plus de réflexion, en utilisant des algorithmes de transformation de Fourier rapides et autres, cela peut être réduit encore plus - une optimisation cruciale lorsque les fonctions utilisées dans zk -Les SNARK ont souvent dans la pratique plusieurs milliers de portes.

Utilisons maintenant l'interpolation de Lagrange pour transformer notre R1CS. Ce que nous allons faire est de prendre la première valeur de chaque vecteur �, d'utiliser l'interpolation de Lagrange pour en faire un polynôme (où l'évaluation du polynôme en � vous donne la première valeur du �ième vecteur), de répéter le processus pour la première valeur de chaque vecteur � et �, puis répétez ce processus pour les deuxièmes valeurs, la troisième, les valeurs, et ainsi de suite. Pour plus de commodité, je vais fournir les réponses maintenant :

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

Les coefficients sont classés par ordre croissant, donc le premier polynôme ci-dessus est en fait 0.833⋅�3—5⋅�2+9.166⋅�−5. Cet ensemble de polynômes (plus un polynôme Z que j'expliquerai plus tard) constitue les paramètres de cette instance QAP particulière. Notez que tout le travail jusqu'à présent ne doit être effectué qu'une seule fois pour chaque fonction que vous essayez d'utiliser zk-SNARK pour vérifier ; une fois les paramètres QAP générés, ils peuvent être réutilisés.

Essayons d'évaluer tous ces polynômes à �=1. Évaluer un polynôme à �=1 signifie simplement additionner tous les coefficients (comme 1�=1 pour tout �), donc ce n'est pas difficile. On a:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

Et voilà, ce que nous avons ici est exactement le même que l’ensemble de trois vecteurs pour la première porte logique que nous avons créée ci-dessus.

Vérification du PAQ

Maintenant, quel est l’intérêt de cette folle transformation ? La réponse est qu'au lieu de vérifier individuellement les contraintes dans le R1CS, nous pouvons désormais vérifier toutes les contraintes en même temps en effectuant la vérification du produit scalaire sur les polynômes.

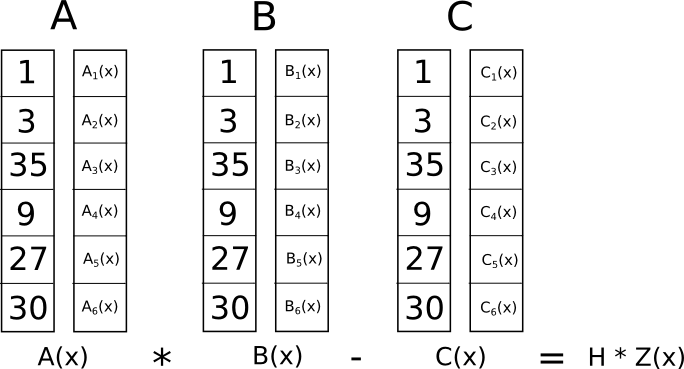
Parce que dans ce cas, la vérification du produit scalaire est une série d’additions et de multiplications de polynômes, le résultat sera lui-même un polynôme. Si le polynôme résultant, évalué à chaque coordonnée � que nous avons utilisée ci-dessus pour représenter une porte logique, est égal à zéro, alors cela signifie que toutes les vérifications réussissent ; si le polynôme résultant évalué à au moins l'une des coordonnées � représentant une porte logique donne une valeur non nulle, alors cela signifie que les valeurs entrant et sortant de cette porte logique sont incohérentes (c'est-à-dire que la porte est �=�⋅�� �1 mais les valeurs fournies pourraient être �=2,���1=2 et �=5).

Notez que le polynôme résultant ne doit pas nécessairement être nul, et en fait, il ne le sera pas dans la plupart des cas ; il peut avoir n'importe quel comportement aux points qui ne correspondent à aucune porte logique, tant que le résultat est nul en tous les points qui do correspondent à une porte. Pour vérifier l'exactitude, nous n'évaluons pas réellement le polynôme �=�.�⋅�.�−�.� en chaque point correspondant à une porte ; au lieu de cela, nous divisons � par un autre polynôme, �, et vérifions que � divise uniformément � – c'est-à-dire que la division �/� ne laisse aucun reste.

� est défini comme (�−1)⋅(�−2)⋅(�−3)… – le polynôme le plus simple qui est égal à zéro en tous les points qui correspondent aux portes logiques. C'est un fait élémentaire de l'algèbre que tous un polynôme égal à zéro en tous ces points doit être un multiple de ce polynôme minimal, et si un polynôme est un multiple de � alors son évaluation en l'un de ces points sera nulle ; cette équivalence facilite grandement notre travail.

Maintenant, effectuons la vérification du produit scalaire avec les polynômes ci-dessus. Tout d’abord, les polynômes intermédiaires :

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

Maintenant, �.�⋅�.�—�.� :

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

Maintenant, le polynôme minimal �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4) :

Z = [24, -50, 35, -10, 1]

Et si on divise le résultat ci-dessus par �, on obtient :

h = t / Z = [-3.666, 17.055, -3.444]

Sans reste.

Nous avons donc la solution pour le QAP. Si nous essayons de falsifier l'une des variables de la solution R1CS à partir de laquelle nous dérivons cette solution QAP - disons, définissons la dernière à 31 au lieu de 30, alors nous obtenons un polynôme � qui échoue à l'une des vérifications (dans ce cas précis). Dans ce cas, le résultat à �=3 serait égal à −1 au lieu de 0), et de plus � ne serait pas un multiple de � ; plutôt, diviser �/� donnerait un reste de [−5.0,8.833,−4.5,0.666].

Notez que ce qui précède est une simplification ; « dans le monde réel », l'addition, la multiplication, la soustraction et la division ne se produiront pas avec des nombres réguliers, mais plutôt avec des éléments de corps finis – une sorte d'arithmétique effrayante qui est cohérente avec elle-même, donc toutes les lois algébriques que nous connaissons et aimons sont toujours est vrai, mais où toutes les réponses sont des éléments d'un ensemble de taille finie, généralement des entiers compris entre 0 et �−1 pour certains �. Par exemple, si �=13, alors 1/2=7 (et 7⋅2=1),3⋅5=2, et ainsi de suite. L'utilisation de l'arithmétique à champs finis élimine le besoin de s'inquiéter des erreurs d'arrondi et permet au système de fonctionner correctement avec des courbes elliptiques, qui finissent par être nécessaires pour le reste de la machinerie zk-SNARK qui rend le protocole zk-SNARK réellement sécurisé.

Un merci spécial à Eran Tromer pour m'avoir aidé à m'expliquer de nombreux détails sur le fonctionnement interne des zk-SNARK.

• Contenu propulsé par le référencement et distribution de relations publiques. Soyez amplifié aujourd'hui.
• PlatoData.Network Ai générative verticale. Autonomisez-vous. Accéder ici.
• PlatoAiStream. Intelligence Web3. Connaissance Amplifiée. Accéder ici.
• PlatonESG. Carbone, Technologie propre, Énergie, Environnement, Solaire, La gestion des déchets. Accéder ici.
• PlatoHealth. Veille biotechnologique et essais cliniques. Accéder ici.
• Décalages de bloc. Modernisation de la propriété des compensations environnementales. Accéder ici.
• La source: Intelligence de données Platon.