Orthonormal Bases Of Extreme Quantumness

Republié par Platon

Suiveurs: 0

Marcin Rudziński^1,2, Adam Burchardt³et la Karol Zyczkowski^1,4

¹Faculté de physique, d'astronomie et d'informatique appliquée, Université Jagellonne, ul. Łojasiewicza 11, 30-348 Cracovie, Pologne
²École doctorale des sciences exactes et naturelles, Université Jagellonne, ul. Łojasiewicza 11, 30-348 Cracovie, Pologne
³QuSoft, CWI et Université d'Amsterdam, Science Park 123, 1098 XG Amsterdam, Pays-Bas
⁴Centre de physique théorique, Académie polonaise des sciences, Al. Lotników 32/46, 02-668 Warszawa, Pologne

Vous trouvez cet article intéressant ou souhaitez en discuter? Scite ou laisse un commentaire sur SciRate.

Abstract

Les états anticohérents de spin ont récemment acquis beaucoup d’attention en tant qu’états les plus « quantiques ». Certains états de spin cohérents et anticohérents sont appelés rotocapteurs quantiques optimaux. Dans ce travail, nous introduisons une mesure du caractère quantique des bases orthonormées des états de spin, déterminée par l'anticohérence moyenne des vecteurs individuels et l'entropie de Wehrl. De cette manière, nous identifions les états les plus cohérents et les plus quantiques, ce qui conduit à des mesures orthogonales de quanticité extrême. Leurs symétries peuvent être révélées à l'aide de la représentation stellaire Majorana, qui fournit une représentation géométrique intuitive d'un état pur par points sur une sphère. Les résultats obtenus conduisent à des bases intriquées au maximum (minimalement) dans le sous-espace symétrique dimensionnel $2j+1$ de l'espace dimensionnel $2^{2j}$ des états des systèmes multipartites composés de qubits $2j$. Certaines bases trouvées sont iso-cohérentes car elles sont constituées de tous les états du même degré de cohérence de spin.

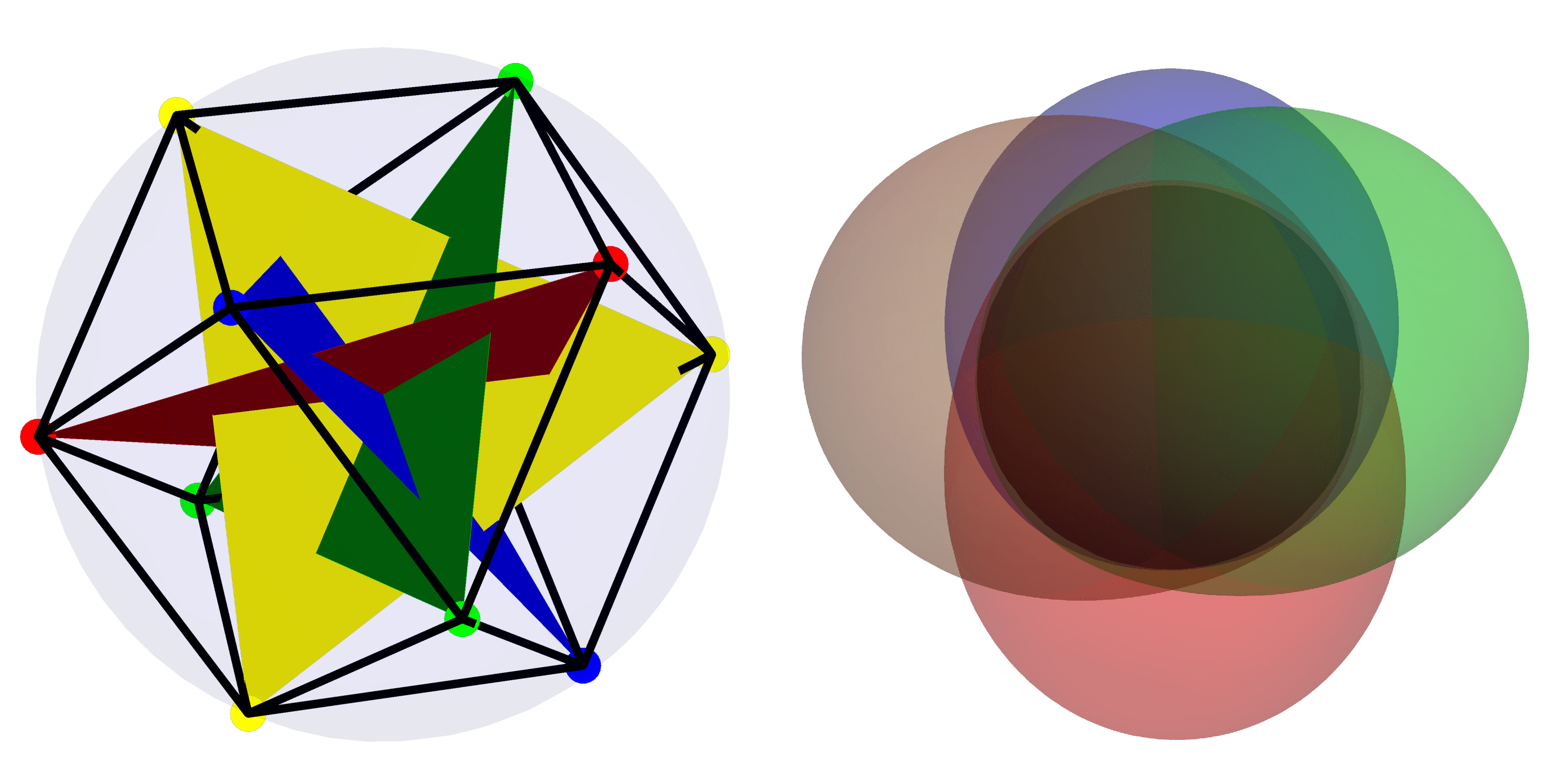
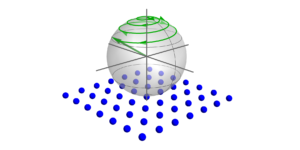
Image présentée : Dans l'image de gauche, la base la plus « quantique » de $mathcal{H}_4$ est représentée à l'aide de la représentation stellaire. À droite, la fonction Husimi pour les états dans la base la plus cohérente (« classique ») au sein de $mathcal{H}_4$ est présentée.

Résumé populaire

Extremal states, coherent and anticoherent, have practical applications in quantum metrology as optimal rotosensors. This work provides a natural extension of previous studies concerning the search for such states proposing optimal orthogonal measurements of Lüders and von Neumann of the extreme spin coherence. We introduce the measure $mathcal{B}_t$ as the tool to characterize the quantumness of a measurement given by a basis in $mathcal{H}_N$. The search for the most quantum bases for $N=3,4,5$ and $7$ is performed. Numerical results suggest, that the obtained solutions are unique. A set of candidates for the “classical” bases consisting of the most spin-coherent states is indicated for $N=3,4,5,6$. Some of the most quantum bases, analyzed in the stellar representation of Majorana, reveal symmetries of Platonic solids. Most classical bases display symmetric structures too. We also considered other measures of the quantumness of vectors forming a given basis. Optimization of the mean Wehrl entropy of $N$ orthogonal vectors leads to the same bases distinguished by extremal values of the quantities $mathcal{B}_t$, with a single exception of the quantum basis for $N=6$.

► Données BibTeX

@article{Rudzinski2024orthonormalbasesof, doi = {10.22331/q-2024-01-25-1234}, url = {https://doi.org/10.22331/q-2024-01-25-1234}, title = {Orthonormal bases of extreme quantumness}, author = {Rudzi{‘{n}}ski, Marcin and Burchardt, Adam and {.{Z}}yczkowski, Karol}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {8}, pages = {1234}, month = jan, year = {2024} }

► Références

T. Frankel, La géométrie de la physique : une introduction, 3e éd., Cambridge University Press (2011).
https: / / doi.org/ 10.1017 / CBO9781139061377

D. Chruściński et A. Jamiołkowski, Phases géométriques en mécanique classique et quantique, Birkhäuser (2004).
https://doi.org/10.1007/978-0-8176-8176-0

DA Lee, Relativité géométrique, American Mathematical Society, Providence (2021).
https: / / doi.org/ 10.1090 / gsm / 201

I. Bengtsson et K. Życzkowski, Géométrie des états quantiques : introduction à l'intrication quantique, 2e éd., Cambridge University Press (2017).
https: / / doi.org/ 10.1017 / 9781139207010

M. Lewin, Méthodes géométriques pour les systèmes quantiques non linéaires à plusieurs corps, J. Functional Analysis 260, 12, (2011).
https: / / doi.org/ 10.1016 / j.jfa.2010.11.017

E. Cohen, H. Larocque, F. Bouchard et al., Phase géométrique d'Aharonov-Bohm à Pancharatnam-Berry et au-delà, Nat. Révérend Phys. 1, 437-449 (2019).
https://doi.org/10.1038/s42254-019-0071-1

E. Majorana Atomi orientati in campo magneto variable, Nuovo Cimento 9, 43-50 (1932).
https: / / doi.org/ 10.1007 / BF02960953

R. Barnett, A. Turner et E. Demler, Classification des nouvelles phases des atomes spineurs, Phys. Le révérend Lett. 97, 180412 (2006).
https: / / doi.org/ 10.1103 / PhysRevLett.97.180412

R. Barnett, A. Turner et E. Demler, Classification des vortex en $S=3$ condensats de Bose-Einstein, Phys. Rév.A 76, 013605 (2007).
https: / / doi.org/ 10.1103 / PhysRevA.76.013605

H. Mäkelä et K.-A. Suominen, États inertes des systèmes spin-s, Phys. Le révérend Lett. 99, 190408 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.190408

E. Serrano-Ensástiga et F. Mireles, Caractérisation de phase des condensats de spineur Bose-Einstein : une approche de représentation stellaire de Majorana, Phys. Lett. Un 492, 129188 (2023).
https: / / doi.org/ 10.1016 / j.physleta.2023.129188

P. Mathonet et al., Équivalence d'intrication des états symétriques $N$-qubit, Phys. Rév.A 81, 052315 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.052315

J. Martin, O. Giraud, PA Braun, D. Braun et T. Bastin, États symétriques multiqubits à fort intrication géométrique, Phys. Rév.A 81, 062347 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.062347

M. Aulbach, DJH Markham et M. Murao, L'état symétrique intriqué au maximum en termes de mesure géométrique, New J. Phys. 12, 073025 (2010).
https://doi.org/10.1088/1367-2630/12/7/073025

DJH Markham, Intrication et symétrie dans les états symétriques par permutation, Phys. Rév.A 83, 042332 (2011).
https: / / doi.org/ 10.1103 / PhysRevA.83.042332

P. Ribeiro et R. Mosseri, Entanglement in the symétrique sector of $n$ qubits, Phys. Le révérend Lett. 106, 180502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.106.180502

M.Aulbach, Classification de l'intrication dans les états symétriques, Int. J. Informations quantiques. 10, 1230004 (2012).
https: / / doi.org/ 10.1142 / S0219749912300045

W. Ganczarek, M. Kuś et K. Życzkowski, Mesure barycentrique de l'intrication quantique, Phys. Rév.A 85, 032314 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.032314

A. Mandilara, T. Coudreau, A. Keller et P. Milman, Classification par intrication d'états symétriques purs via des états cohérents de spin, Phys. Rév.A 90, 050302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.050302

P. Hyllus, et al., Informations de Fisher et intrication multiparticulaire, Phys. Rév.A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

JH Hannay, La phase Berry pour le spin dans la représentation Majorana, J. Phys. R : Mathématiques. Gén. 31, L53 (1998).
https://doi.org/10.1088/0305-4470/31/2/002

P. Bruno, Phase géométrique quantique dans la représentation stellaire de Majorana : cartographie sur une phase Aharonov-Bohm à plusieurs corps, Phys. Le révérend Lett. 108, 240402 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.240402

HD Liu et LB Fu, Phase de Berry et intrication quantique dans la représentation stellaire de Majorana, Phys. Rév.A 94, 022123 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.022123

P. Ribeiro, J. Vidal et R. Mosseri, Limite thermodynamique du modèle Lipkin-Meshkov-Glick, Phys. Le révérend Lett. 99, 050402 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.050402

P. Ribeiro, J. Vidal et R. Mosseri, Spectre exact du modèle Lipkin-Meshkov-Glick dans la limite thermodynamique et corrections de taille finie, Phys. Rév.E 78, 021106 (2008).
https: / / doi.org/ 10.1103 / PhysRevE.78.021106

J. Zimba, États de spin « anticohérents » via la représentation Majorana, Electron. J. Théor. Phys. 3, 143 (2006).
https:///api.semanticscholar.org/CorpusID:13938120

D. Baguette, T. Bastin et J. Martin, États symétriques à plusieurs bits avec des réductions d'un qubit maximales mélangées, Phys. Rev. A 90, 032314 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.032314

O. Giraud, D. Braun, D. Baguette, T. Bastin et J. Martin, Tensor représentation of spin states, Phys. Rev. Lett. 114, 080401 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.080401

D. Baguette, F. Damanet, O. Giraud et J. Martin, Anticoherence of spin states with point-group symmetries, Phys. Rév.A 92, 052333 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.92.052333

HD Liu, LB Fu, X. Wang, Approche d'état cohérent pour la représentation Majorana, Commun. Théorique. Phys. 67, 611 (2017).
https://doi.org/10.1088/0253-6102/67/6/611

D. Baguette et J. Martin, Mesures d'anticohérence pour les états de spin purs, Phys. Rév.A 96, 032304 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.032304

P. Kolenderski et R. Demkowicz-Dobrzański, État optimal pour maintenir les référentiels alignés et les solides platoniciens, Phys. Rév.A 78, 052333 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052333

C. Chryssomalakos et H. Hernández-Coronado, Rotocapteurs quantiques optimaux, Phys. Rév.A 95, 052125 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.95.052125

AZ Goldberg et DFV James, Mesures d'angle d'Euler limitées quantiquement à l'aide d'états anticohérents, Phys. Rév.A 98, 032113 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032113

J. Martin, S. Weigert et O. Giraud, Détection optimale des rotations autour d'axes inconnus par des états cohérents et anticohérents, Quantum 4, 285 (2020).
https://doi.org/10.22331/q-2020-06-22-285

J. Crann, DW Kribs et R. Pereira, Conceptions sphériques et états de spin anticohérents, J. Phys. R : Mathématiques. Théorique. 43, 255307 (2010).
https://doi.org/10.1088/1751-8113/43/25/255307

E. Bannai et M. Tagami, Une note sur les états de spin anticohérents, J. Phys. R : Mathématiques. Théorique. 44, 342002 (2011).
https://doi.org/10.1088/1751-8113/44/34/342002

M. Wang et Y. Zhu, États anticohérents de spin-2 et conceptions sphériques, J. Phys. R : Mathématiques. Théorique. 55, 425304 (2022).
https:///doi.org/10.1088/1751-8121/ac971d

AZ Goldberg, AB Klimov, M.Grassl, G. Leuchs et LL Sánchez-Soto, États quantiques extrêmes, AVS Quantum Sci. 2, 044701 (2020).
https: / / doi.org/ 10.1116 / 5.0025819

AZ Goldberg, M. Grassl, G. Leuchs et LL Sánchez-Soto, Le quantum au-delà de l'intrication : le cas des états symétriques, Phys. Rév.A 105, 022433 (2022).
https: / / doi.org/ 10.1103 / PhysRevA.105.022433

O. Giraud, P. Braun et D. Braun, Quantification du quantum et quête des reines du quantum, New J. Phys. 12, 063005 (2010).
https://doi.org/10.1088/1367-2630/12/6/063005

R. Delbourgo, États d'incertitude minimale pour le groupe de rotation et les groupes alliés, J. Phys. Un 10, L233 (1977).
https://doi.org/10.1088/0305-4470/10/11/012

A. Wehrl, Sur la relation entre l'entropie classique et la mécanique quantique, Rep. Math. Phys. 16, 353 (1979).
https://doi.org/10.1016/0034-4877(79)90070-3

EH Lieb, Preuve d'une conjecture entropique de Wehrl, Commun. Mathématiques. Phys. 62, 35 (1978).
https: / / doi.org/ 10.1007 / BF01940328

CT Lee, l'entropie des états de spin de Wehrl et la conjecture de Lieb, J. Phys. A 21, 3749 (1988).
https://doi.org/10.1088/0305-4470/21/19/013

EH Lieb et JP Solovej, Preuve d'une conjecture d'entropie pour les états de spin cohérents de Bloch et ses généralisations, Acta Math. 212, 379 (2014).
https://doi.org/10.1007/s11511-014-0113-6

F. Bouchard, et al., Métrologie quantique à la limite avec les constellations extrémales de Majorana, Optica 4, 1429-1432 (2017).
https: / / doi.org/ 10.1364 / OPTICA.4.001429

A. Wehrl, Propriétés générales de l'entropie, Rev. Mod. Phys. 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

A. Wehrl, Les nombreuses facettes de l'entropie, Rep. Math. Phys. 30, 119 (1991).
https://doi.org/10.1016/0034-4877(91)90045-O

S. Gnutzmann et K. Życzkowski, Les entropies de Renyi-Wehrl comme mesures de localisation dans l'espace des phases, J. Phys. A 34, 10123 (2001).
https://doi.org/10.1088/0305-4470/34/47/317

K. Życzkowski, Localisation des états propres et entropie moyenne de Wehrl, Physica E 9, 583 (2001).
https://doi.org/10.1016/S1386-9477(00)00266-6

LL Sánchez-Soto, AB Klimov, P. de la Hoz et G. Leuchs, États de polarisation quantique contre états de polarisation classiques : quand les multipôles comptent, J. Phys. B46 104011 (2013).
https://doi.org/10.1088/0953-4075/46/10/104011

A. Tavakoli et N. Gisin, Les solides platoniciens et tests fondamentaux de la mécanique quantique, Quantum 4, 293 (2020).
https://doi.org/10.22331/q-2020-07-09-293

H. Ch. Nguyen, S. Designolle, M. Barakat et O. Gühne, Symmétries entre mesures en mécanique quantique, préimpression arXiv :2003.12553 (2022).
https:///doi.org/10.48550/arXiv.2003.12553
arXiv: 2003.12553

JI Latorre et G. Sierra, Intrication platonicienne, Quantum Inf. Calculer. 21, 1081 (2021).
https: / / doi.org/ 10.26421 / QIC21.13-14-1

K. Bolonek-Lasoń et P. Kosiński, Groupes, solides platoniciens et inégalités de Bell, Quantum 5, 593 (2021).
https://doi.org/10.22331/q-2021-11-29-593

KF Pál et T. Vértesi, Groupes, Inégalités platoniciennes de Bell pour toutes les dimensions, Quantum 6, 756 (2022).
https://doi.org/10.22331/q-2022-07-07-756

RH Dicke, Cohérence dans les processus de rayonnement spontané, Phys. Rév.93, 99 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99

V. Karimipour et L. Memarzadeh, Bases équienchevêtrées en dimensions arbitraires Phys. Rév.A 73, 012329 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.73.012329

G. Rajchel, A. Gąsiorowski et K. Życzkowski, Matrices Hadamard robustes, rayons unistochastiques dans le polytope de Birkhoff et bases équi-intriquées dans les espaces composites Math. Comp. Sci. 12, 473 (2018).
https: / / doi.org/ 10.1007 / s11786-018-0384-y

J. Czartowski, D. Goyeneche, M. Grassl et K. Życzkowski, Bases isointriquées mutuellement impartiales, mesures quantiques symétriques et conceptions à états mixtes, Phys. Le révérend Lett. 124, 090503 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.124.090503

F. Del Santo, J. Czartowski, K. Życzkowski et N. Gisin, Bases iso-enchevêtrées et mesures conjointes, préimpression arXiv :2307.06998 (2023).
https:///doi.org/10.48550/arXiv.2307.06998
arXiv: 2307.06998

R. Penrose, Sur la non-localité de Bell sans probabilités : une curieuse géométrie, Quantum Reflections (2000).

J. Zimba et R. Penrose, On Bell non-localité sans probabilités : géométrie plus curieuse, Stud. Hist. Phil. Sci. 24, 697 (1993).
https://doi.org/10.1016/0039-3681(93)90061-N

JE Massad et PK Aravind, Le dodécaèdre de Penrose revisité, Am. J. Physique 67, 631 (1999).
https: / / doi.org/ 10.1119 / 1.19336

K. Husimi, Quelques propriétés formelles de la matrice de densité, Proc. Phys. Mathématiques. Soc. 22, 264 (1940).
https: / / doi.org/ 10.11429 / ppmsj1919.22.4_264

W. Słomczyński et K. Życzkowski, L'entropie dynamique moyenne des cartes quantiques sur la sphère diverge dans la limite semi-classique, Phys. Le révérend Lett. 80, 1880 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.1880

M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, Rapporteurs quantiques parfaits, préimpression arXiv :2310.13045 (2023).
https:///doi.org/10.48550/arXiv.2310.13045
arXiv: 2310.13045

Site Web de NCN Maestro 7 2015/18/A/ST2/00274 https://chaos.if.uj.edu.pl/ karol/Maestro7/files/data3/Numerical_Results.dat.
https:///chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

D. Weingarten, Comportement asymptotique des intégrales de groupe dans la limite du rang infini, J. Math. Phys. 19, 999 (1978).
https: / / doi.org/ 10.1063 / 1.523807

B. Collins et P. Śniady, Intégration par rapport à la mesure Haar sur le groupe unitaire, orthogonal et symplectique, Commun. Mathématiques. Phys. 264, 773 (2006).
https://doi.org/10.1007/s00220-006-1554-3

G. Rajchel, Cartographies et conceptions quantiques, thèse de doctorat, préimpression arXiv :2204.13008 (2022).
https:///doi.org/10.48550/arXiv.2204.13008
arXiv: 2204.13008

D. Martin et EP Wigner, Théorie des groupes et son application à la mécanique quantique des spectres atomiques, Academic Press Inc. NY (1959).
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

Cité par

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny et Kamil Korzekwa, « Rapporteurs quantiques parfaits », arXiv: 2310.13045, (2023).

[2] Aaron Z. Goldberg, « Corrélations pour des sous-ensembles de particules dans des états symétriques : que font les photons dans un faisceau de lumière lorsque les autres sont ignorés », arXiv: 2401.05484, (2024).

Les citations ci-dessus proviennent de SAO / NASA ADS (dernière mise à jour réussie 2024-01-25 11:53:23). La liste peut être incomplète car tous les éditeurs ne fournissent pas de données de citation appropriées et complètes.

Impossible de récupérer Données de référence croisée lors de la dernière tentative 2024-01-25 11:53:22: Impossible de récupérer les données citées par 10.22331 / q-2024-01-25-1234 de Crossref. C'est normal si le DOI a été enregistré récemment.

Cet article est publié dans Quantum sous le Creative Commons Attribution 4.0 International (CC BY 4.0) Licence. Le droit d'auteur reste la propriété des détenteurs d'origine tels que les auteurs ou leurs institutions.

Contenu propulsé par le référencement et distribution de relations publiques. Soyez amplifié aujourd'hui.
PlatoData.Network Ai générative verticale. Autonomisez-vous. Accéder ici.
PlatoAiStream. Intelligence Web3. Connaissance Amplifiée. Accéder ici.
PlatonESG. Carbone, Technologie propre, Énergie, Environnement, Solaire, La gestion des déchets. Accéder ici.
PlatoHealth. Veille biotechnologique et essais cliniques. Accéder ici.
La source: https://quantum-journal.org/papers/q-2024-01-25-1234/

Horodatage: 25 janvier 2024

Horodatage: Le 3 octobre 2023

Bases orthonormales de quanticité extrême

Republié par Platon

Abstract

Résumé populaire

► Données BibTeX

► Références

Cité par

Plus de Journal quantique

Protocoles DIQKD améliorés avec analyse de taille finie

Génération d'enchevêtrement télécommandée

Coupure de circuit quantique rapide avec des mesures aléatoires

Génération et préservation basées sur la mesure des états de chat et de grille dans un état de cluster à variable continue

Préparation d'état dans le modèle de Heisenberg par spirale adiabatique

MQT Bench : logiciel d'analyse comparative et outils d'automatisation de la conception pour l'informatique quantique

Les contraintes d'analyticité limitent la décroissance du facteur de forme spectral

Solutions variationnelles aux mappages fermion-qubit en deux dimensions spatiales

Simulation d'une précision prouvée des théories de jauge et des systèmes bosoniques

Codage et analyse quantiques sur un processus stochastique en temps continu avec des applications financières

À propos de nous

Recherche verticale et Ai

Plateforme

Restez à l'affût

Compte