[Peegel] Ruutarvulised aritmeetilised programmid: nullist kangelaseni

Vitalik Buterin kaudu Vitalik Buterini ajaveeb

See on postituse peegel aadressil https://medium.com/@VitalikButerin/ruutarvulised-aritmeetilised-programmid-null-kangelaseni-f6d558cea649

Viimasel ajal on zk-SNARKide taga oleva tehnoloogia vastu palju huvi tundnud ja inimesed tunnevad seda üha enam üritab demüstifitseerida midagi, mida paljud on hakatud nimetama kuu matemaatikaks selle tajutava lahutamatu keerukuse tõttu. zk-SNARKide mõistmine on tõepoolest üsna keeruline, eriti suure hulga liikuvate osade tõttu, mis peavad kogu asja toimimiseks kokku tulema, kuid kui me tehnoloogiat tükkhaaval tükeldame, muutub selle mõistmine lihtsamaks.

Selle postituse eesmärk ei ole olla zk-SNARKide täielik sissejuhatus; see eeldab taustateadmisena, et (i) te teate, mis on zk-SNARK-id ja mida nad teevad, ja (ii) teate piisavalt matemaatikat, et saaksite arutleda selliste asjade kohta nagu polünoomid (kui väide �(�)+�(�) =(�+�)(�) , kus � ja � on polünoomid, tundub teile loomulik ja ilmne, siis olete õigel tasemel). Pigem kaevab postitus sügavamale tehnoloogia taga olevatesse masinatesse ja püüab võimalikult hästi selgitada torujuhtme esimest poolt, nagu on joonistanud zk-SNARKI teadur Eran Tromer:

Siinsed sammud saab jagada kaheks pooleks. Esiteks ei saa zk-SNARK-e otseselt ühelegi arvutusprobleemile rakendada; pigem peate probleemi teisendama õigeks "vormiks", et probleem toimiks. Seda vormi nimetatakse ruutarvuliseks programmiks (QAP) ja funktsiooni koodi teisendamine üheks neist on iseenesest väga ebatriviaalne. Funktsiooni koodi QAP-ks teisendamise protsessi kõrval on veel üks protsess, mida saab käivitada, nii et kui teil on koodi sisend, saate luua vastava lahenduse (mõnikord nimetatakse seda QAP-i tunnistajaks). Pärast seda on veel üks üsna keerukas protsess selle tunnistaja jaoks tegeliku "nullteadmiste tõendi" loomiseks ja eraldi protsess tõendite kontrollimiseks, et keegi teine ​​teile edastab, kuid need on üksikasjad, mis selle postituse jaoks ei kuulu. .

Näide, mille valime, on lihtne: tõestades, et teate kuupvõrrandi lahendit: �3+�+5=35 (vihje: vastus on 3). See probleem on piisavalt lihtne, et tulemuseks olev QAP ei oleks nii suur, et oleks hirmutav, kuid piisavalt mittetriviaalne, et saaksite näha, kuidas kõik masinad mängu tulevad.

Kirjutame oma funktsiooni järgmiselt:

def qeval(x):
    y = x**3
    return x + y + 5

Lihtne eriotstarbeline programmeerimiskeel, mida me siin kasutame, toetab põhiaritmeetikat (+, −, ⋅, /), konstantse võimsusega astendamist (�7, kuid mitte ��) ja muutujate omistamist, mis on piisavalt võimas, et teoreetiliselt seda teha saab. mis tahes arvutus selle sees (seni, kuni arvutusastmete arv on piiratud; silmused pole lubatud). Pange tähele, et moodulite (%) ja võrdlustehteid (<, >, ≤, ≥) EI toetata, kuna lõpliku tsüklilise rühma aritmeetikas pole tõhusat viisi mooduli või võrdluse tegemiseks (olge selle eest tänulik, kui see oli võimalik). kui teha kumbagi, katkeb elliptilise kõvera krüptograafia kiiremini, kui võite öelda "binaarotsing" ja "Hiina jäägiteoreem").

Keelt saab laiendada moodulitele ja võrdlustele, pakkudes abisisenditena bittide jaotusi (nt 13=23+22+1), tõestades nende jaotuste õigsust ja tehes matemaatikat binaarahelates; Lõpliku välja aritmeetikas on ka võrdsuse (==) kontrollide tegemine tehtav ja tegelikult natuke lihtsam, kuid need on mõlemad detailid, millesse me praegu ei hakka. Saame laiendada keelt tingimuslausete toetamiseks (nt kui �<5:�=7; muidu: �=9), teisendades need aritmeetiliseks vormiks: �=7⋅(�<5)+9⋅(�≥5 ), kuid pange tähele, et tingimuslause mõlemad "teed" tuleb täita ja kui teil on palju pesastatud tingimustingimusi, võib see kaasa tuua palju üldkulusid.

Vaatame nüüd seda protsessi samm-sammult läbi. Kui soovite seda mõne koodilõigu jaoks ise teha, siis ma rakendas siin kompilaatorit (ainult hariduslikel eesmärkidel; pole veel valmis reaalsete zk-SNARKide jaoks QAP-ide tegemiseks!).

Lamestamine

Esimene samm on lamestamisprotseduur, mille käigus teisendame algse koodi, mis võib sisaldada meelevaldselt keerulisi lauseid ja avaldisi, kahes vormis avalduste jadaks: �=� (kus � võib olla muutuja või arv ) ja �=� (��) � (kus �� võib olla +, −, ⋅, / ning � ja � võivad olla muutujad, arvud või ise alamväljendid). Kõiki neid väiteid võib pidada vooluringi loogilisteks väravateks. Ülaltoodud koodi tasandusprotsessi tulemus on järgmine:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

Kui loete algset koodi ja koodi siin, näete üsna hõlpsalt, et need kaks on samaväärsed.

Väravad R1CS-i

Nüüd teisendame selle millekski, mida nimetatakse auaste 1 piirangusüsteemiks (R1CS). R1CS on kolme vektori (�, �, �) rühmade jada ja R1CS-i lahendus on vektor �, kus � peab täitma võrrandi �.�⋅�.�−�.�=0, kus . tähistab punktkorrutist – lihtsamalt öeldes, kui me "tõmbutame kokku" � ja �, korrutades kaks samades positsioonides olevat väärtust ja seejärel võtame nende korrutiste summa, siis teeme sama väärtusega � ja � ning seejärel � ja � , siis võrdub kolmas tulemus kahe esimese tulemuse korrutisega. Näiteks on see rahulolev R1CS:

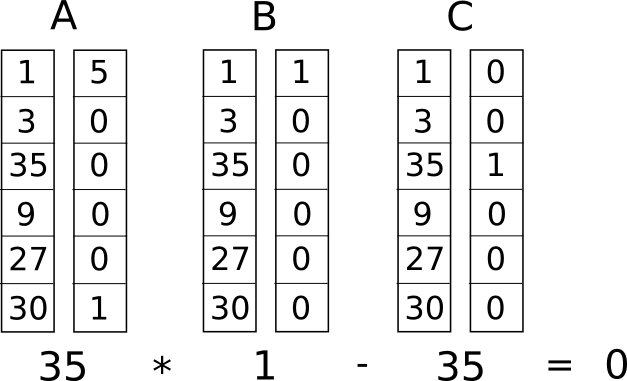
Kuid selle asemel, et omada ainult ühte piirangut, on meil palju piiranguid: üks iga loogikavärava jaoks. Loogikavärava (�,�,�) kolmikuks teisendamiseks on standardne viis, olenevalt sellest, milline on tehte (+, −, ⋅ või /) ja kas argumendid on muutujad või numbrid. Iga vektori pikkus võrdub muutujate koguarvuga süsteemis, sealhulgas näivmuutuja ~üks esimese indeksi juures, mis tähistab arvu 1, sisendmuutujad, näivmuutuja ~out, mis esindab väljundit ja seejärel kõik vahepealsed muutujad (���1 ja ���2 eespool); vektorid on üldiselt väga hõredad, täites ainult need pesad, mis vastavad muutujatele, mida mingi konkreetne loogikavärav mõjutab.

Esiteks pakume muutuja vastendamist, mida kasutame:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

Lahendusvektor koosneb kõigi nende muutujate määramistest selles järjekorras.

Nüüd anname esimese värava (�,�,�) kolmiku:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

Näete, et kui lahendusvektor sisaldab teises positsioonis 3 ja neljandas positsioonis 9, siis olenemata lahendusvektori ülejäänud sisust taandub punktkorrutise kontroll väärtusele 3⋅3=9 ja nii et see läheb üle. Kui lahendusvektoril on teisel positsioonil −3 ja neljandal 9, läheb ka kontroll läbi; tegelikult, kui lahendusvektori teises positsioonis on 7 ja neljandas positsioonis 49, siis see kontroll ikkagi läbib – selle esimese kontrolli eesmärk on kontrollida ainult esimese värava sisendite ja väljundite järjepidevust.

Liigume nüüd teise värava juurde:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

Sarnases stiilis esimese punktiga tootekontrolliga kontrollime siin, et ���1⋅�=�.

Nüüd kolmas värav:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

Siin on muster mõnevõrra erinev: see korrutab lahendusvektori esimese elemendi teise elemendiga, seejärel viienda elemendiga, lisab kaks tulemust ja kontrollib, kas summa võrdub kuuenda elemendiga. Kuna lahendusvektori esimene element on alati üks, on see lihtsalt liitmise kontroll, mis kontrollib, kas väljund võrdub kahe sisendi summaga.

Lõpuks neljas värav:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

Siin hindame viimast kontrolli, ~out =���2+5. Punktkorrutise kontroll toimib nii, et võtab lahendusvektoris kuuenda elemendi, lisab esimese elemendi viis korda (meeldetuletus: esimene element on 1, seega tähendab see sisuliselt 5 lisamist) ja kontrollib seda kolmanda elemendi suhtes, mis on koht, kus me salvestada väljundmuutuja.

Ja seal on meie R1CS nelja piiranguga. Tunnistaja on lihtsalt kõigi muutujate määramine, sealhulgas sisend, väljund ja sisemised muutujad:

[1, 3, 35, 9, 27, 30]

Saate selle ise välja arvutada, lihtsalt "käitades" ülaltoodud lamestatud koodi, alustades sisendmuutujate määramisest �=3 ja sisestades arvutamisel kõigi vahepealsete muutujate väärtused ja väljundi.

Täielik R1CS on kokku pandud:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS kuni QAP

Järgmine samm on selle R1CS-i võtmine ja teisendamine QAP-vormingusse, mis rakendab täpselt sama loogikat, välja arvatud polünoomide kasutamine punktproduktide asemel. Teeme seda järgmiselt. Läheme 3 neljast kolmest vektori pikkusest kuue vektori rühmast kuue rühma kolme 3-astmelise polünoomiga, kus hinnatakse iga polünoomi. x koordinaat esindab ühte piirangutest. See tähendab, et kui hindame polünoomide väärtust �=1, siis saame oma esimese vektorite komplekti, kui hindame polünoomid väärtusega �=2, siis saame teise vektorite komplekti ja nii edasi.

Saame selle teisenduse teha kasutades midagi, mida nimetatakse a Lagrange'i interpolatsioon. Probleem, mille Lagrange'i interpolatsioon lahendab, on järgmine: kui teil on hulk punkte (st (�,�) koordinaadipaare), siis nende punktide Lagrange'i interpoleerimine annab polünoomi, mis läbib kõiki neid punkte. Teeme seda ülesande dekomponeerimisega: loome iga koordinaadi jaoks polünoomi, millel on soovitud koordinaat sellel koordinaadil ja koordinaadil 0 kõigil teistel koordinaatidel, mis meid huvitavad, ning seejärel saada lõplik. tulemuseks liidame kõik polünoomid kokku.

Teeme näite. Oletame, et tahame polünoomi, mis läbib (1,3), (2,2) ja (3,4). Alustuseks teeme polünoomi, mis läbib (1,3), (2,0) ja (3,0). Nagu selgub, on lihtne teha polünoomi, mis "torkab välja" väärtusel �=1 ja on null teistes huvipunktides; me lihtsalt teeme:

(x - 2) * (x - 3)

Mis näeb välja selline:

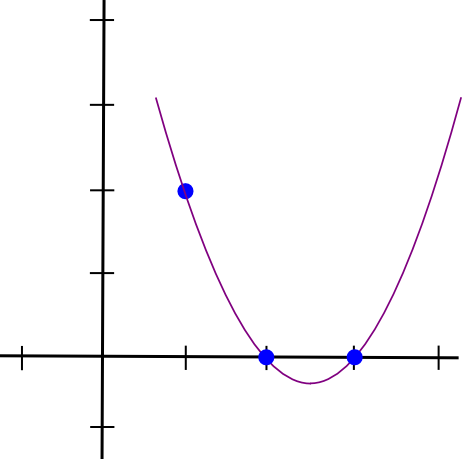
Nüüd peame selle lihtsalt ümber mõõtma, et kõrgus x=1 oleks õige:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

See annab meile:

1.5 * x**2 - 7.5 * x + 9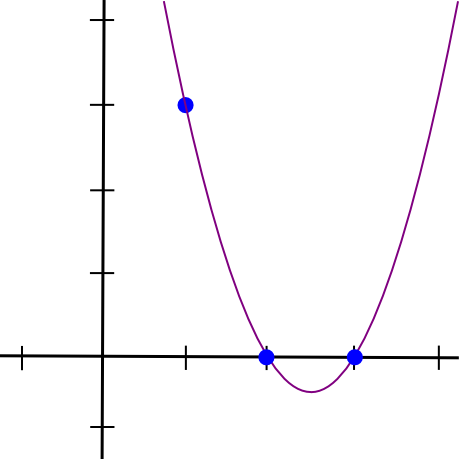

Seejärel teeme sama kahe ülejäänud punktiga ja saame veel kaks sarnase välimusega polünoomi, välja arvatud see, et need jäävad �=2 ja �=3 asemel välja �=1 asemel. Liidame kõik kolm kokku ja saame:

1.5 * x**2 - 5.5 * x + 7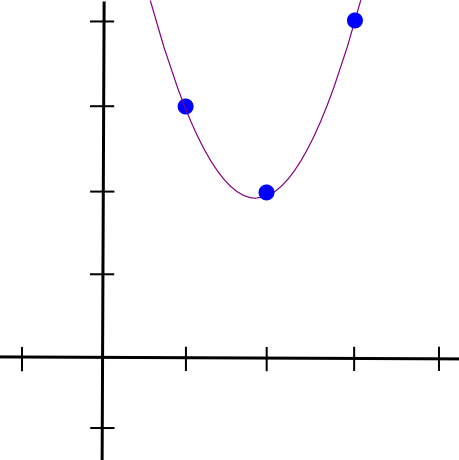

Täpselt selliste koordinaatidega, mida me tahame. Ülalkirjeldatud algoritm võtab �(�3) aega, kuna punkte on � ja iga punkt nõuab �(�2) aega, et polünoomid omavahel korrutada; vähese mõtlemisega saab seda lühendada �(�) ajale ja palju rohkem mõtlemisega, kasutades kiireid Fourier' teisendusalgoritme ja muud sarnast, saab seda veelgi vähendada – see on ülioluline optimeerimine, kui funktsioonid, mis harjuvad zk-s -SNARKidel on praktikas sageli mitu tuhat väravat.

Nüüd kasutame oma R1CS-i teisendamiseks Lagrange'i interpolatsiooni. Me võtame igast � vektorist välja esimese väärtuse, kasutame Lagrange'i interpolatsiooni, et teha sellest polünoomi (kus polünoomi väärtus � annab �nda � vektori esimese väärtuse), korda protsessi. iga � ja � vektori esimese väärtuse jaoks ning seejärel korrake seda protsessi teiste väärtuste, kolmanda väärtuste ja nii edasi. Mugavuse huvides annan kohe vastused:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

Koefitsiendid on kasvavas järjekorras, seega on ülaltoodud esimene polünoom tegelikult 0.833⋅�3—5⋅�2+9.166⋅�−5. See polünoomide komplekt (pluss Z-polünoom, mida selgitan hiljem) moodustab selle konkreetse QAP-i eksemplari parameetrid. Pange tähele, et kogu töö kuni selle punktini tuleb teha ainult üks kord iga funktsiooni jaoks, mille kontrollimiseks proovite zk-SNARK-e kasutada; kui QAP parameetrid on loodud, saab neid uuesti kasutada.

Proovime kõiki neid polünoome hinnata väärtusega �=1. Polünoomi hindamine väärtusega �=1 tähendab lihtsalt kõigi koefitsientide liitmist (nagu 1�=1 kõigi � jaoks), seega pole see keeruline. Saame:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

Ja ennäe, see, mis meil siin on, on täpselt sama, mis kolme vektori kogum esimese loogikavärava jaoks, mille me ülal lõime.

QAP kontrollimine

Mis selle hullumeelse ümberkujundamise mõte nüüd on? Vastus on, et R1CS-i piirangute eraldi kontrollimise asemel saame nüüd kontrollida kõik piirangud korraga tehes toote punktikontrolli polünoomide kohta.

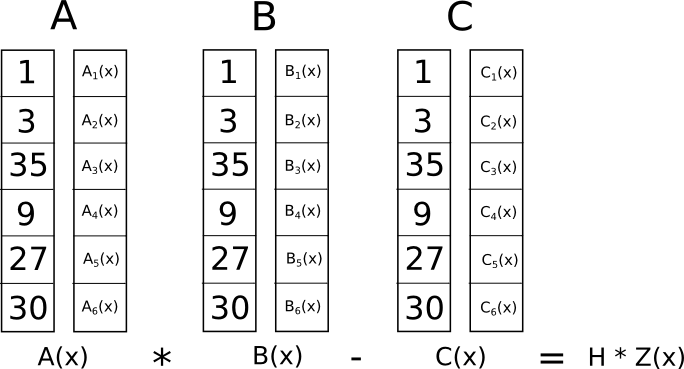
Kuna antud juhul on punktkorrutise kontroll polünoomide liitmise ja korrutamise jada, on tulemuseks ise polünoom. Kui saadud polünoom, mida hinnati igal � koordinaadil, mida me ülalpool loogikavärava esitamiseks kasutasime, on võrdne nulliga, tähendab see, et kõik kontrollid läbivad; kui saadud polünoom, mis on hinnatud vähemalt ühel loogilist väravat esindavatest � koordinaatidest, annab nullist erineva väärtuse, tähendab see, et sellesse loogilisse väravasse sisenevad ja sealt väljuvad väärtused on vastuolulised (st värav on �=�⋅�� �1, kuid esitatud väärtused võivad olla �=2,���1=2 ja �=5).

Pange tähele, et saadud polünoom ise ei pea olema null ja tegelikult ei pea seda olema; see võib käituda mis tahes punktides, mis ei vasta ühelegi loogilisele väravale, kui tulemus on null kõigis punktides, mis do vastavad mõnele väravale. Õigsuse kontrollimiseks ei hinda me tegelikult polünoomi �=�.�⋅�.�−�.� igas väravale vastavas punktis; selle asemel jagame � teise polünoomiga � ja kontrollime, et � jagaks ühtlaselt � – see tähendab, et jagamine �/� ei jäta jääki.

� on defineeritud kui (�−1)⋅(�−2)⋅(�−3)… – kõige lihtsam polünoom, mis on kõigis loogikaväravatele vastavates punktides võrdne nulliga. See on algebra elementaarne fakt mistahes polünoom, mis on kõigis nendes punktides võrdne nulliga, peab olema selle minimaalse polünoomi kordne, ja kui polünoom on � kordne, siis on selle hinnang mis tahes punktis null; see samaväärsus teeb meie töö palju lihtsamaks.

Nüüd kontrollime punktkorrutist ülaltoodud polünoomidega. Esiteks, vahepealsed polünoomid:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

Nüüd, �.�⋅�.�—�.�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

Nüüd minimaalne polünoom �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):

Z = [24, -50, 35, -10, 1]

Ja kui jagame ülaltoodud tulemuse �-ga, saame:

h = t / Z = [-3.666, 17.055, -3.444]

Ilma jäägita.

Ja seega on meil QAP-i jaoks lahendus. Kui proovime võltsida mõnda muutujat R1CS-i lahenduses, millest tuletame selle QAP-lahenduse – näiteks seadke viimaseks 31 asemel 30, siis saame � polünoomi, mis läbib ühe kontrolli (selles konkreetses juhul �=3 oleks tulemus 1 asemel −0) ja pealegi ei oleks � arvu � kordne; pigem annaks �/� jagamisel jääk [−5.0,8.833,−4.5,0.666].

Pange tähele, et ülaltoodud on lihtsustus; "reaalses maailmas" ei toimu liitmine, korrutamine, lahutamine ja jagamine mitte tavaarvude, vaid pigem lõplike väljaelementidega - see on õudne aritmeetika, mis on isejärjekindel, nii et kõik algebralised seadused, mida me teame ja armastame, jäävad endiselt kehtib, kuid kus kõik vastused on mõne lõpliku suurusega hulga elemendid, tavaliselt täisarvud vahemikus 0 kuni �−1 mõne � puhul. Näiteks kui �=13, siis 1/2=7 (ja 7⋅2=1),3⋅5=2 ja nii edasi. Lõpliku välja aritmeetika kasutamine eemaldab vajaduse muretseda ümardamisvigade pärast ja võimaldab süsteemil kenasti töötada elliptiliste kõveratega, mis on lõpuks vajalikud ülejäänud zk-SNARKi masinate jaoks, mis muudavad zk-SNARKi protokolli tegelikult turvaliseks.

Eriline tänu Eran Tromerile, kes aitas mulle selgitada palju üksikasju zk-SNARKide sisemise toimimise kohta.

• SEO-põhise sisu ja PR-levi. Võimenduge juba täna.
• PlatoData.Network Vertikaalne generatiivne Ai. Jõustage ennast. Juurdepääs siia.
• PlatoAiStream. Web3 luure. Täiustatud teadmised. Juurdepääs siia.
• PlatoESG. Süsinik, CleanTech, Energia, Keskkond päikeseenergia, Jäätmekäitluse. Juurdepääs siia.
• PlatoTervis. Biotehnoloogia ja kliiniliste uuringute luureandmed. Juurdepääs siia.
• BlockOffsets. Keskkonnakompensatsiooni omandi ajakohastamine. Juurdepääs siia.
• Allikas: Platoni andmete intelligentsus.