Bases ortonormales de la cuántica extrema

Reeditado por Platón

seguidores: 0

Marcin Rudziński^1,2, Adam Burchardt³y Karol Zyczkowski^1,4

¹Facultad de Física, Astronomía e Informática Aplicada, Universidad Jagiellonian, ul. Łojasiewicza 11, 30-348 Cracovia, Polonia
²Escuela de Doctorado en Ciencias Exactas y Naturales, Universidad Jagellónica, ul. Łojasiewicza 11, 30-348 Cracovia, Polonia
³QuSoft, CWI y Universidad de Amsterdam, Science Park 123, 1098 XG Amsterdam, Países Bajos
⁴Centro de Física Teórica, Academia Polaca de Ciencias, Al. Lotników 32/46, 02-668 Warszawa, Polonia

¿Encuentra este documento interesante o quiere discutirlo? Scite o deje un comentario en SciRate.

Resumen

Los estados spin-anticoherentes han adquirido recientemente mucha atención como los estados más "cuánticos". Algunos estados de espín coherentes y anticoherentes se conocen como rotosensores cuánticos óptimos. En este trabajo, introducimos una medida de cuántica para bases ortonormales de estados de espín, determinada por la anticoherencia promedio de vectores individuales y la entropía de Wehrl. De esta manera, identificamos los estados más coherentes y más cuánticos, que conducen a mediciones ortogonales de cuántica extrema. Sus simetrías pueden revelarse utilizando la representación estelar de Majorana, que proporciona una representación geométrica intuitiva de un estado puro mediante puntos en una esfera. Los resultados obtenidos conducen a bases entrelazadas máxima (mínimamente) en el subespacio simétrico dimensional $2j+1$ del espacio dimensional $2^{2j}$ de estados de sistemas multipartitos compuestos por qubits $2j$. Algunas bases encontradas son isocoherentes ya que constan de todos los estados del mismo grado de coherencia de espín.

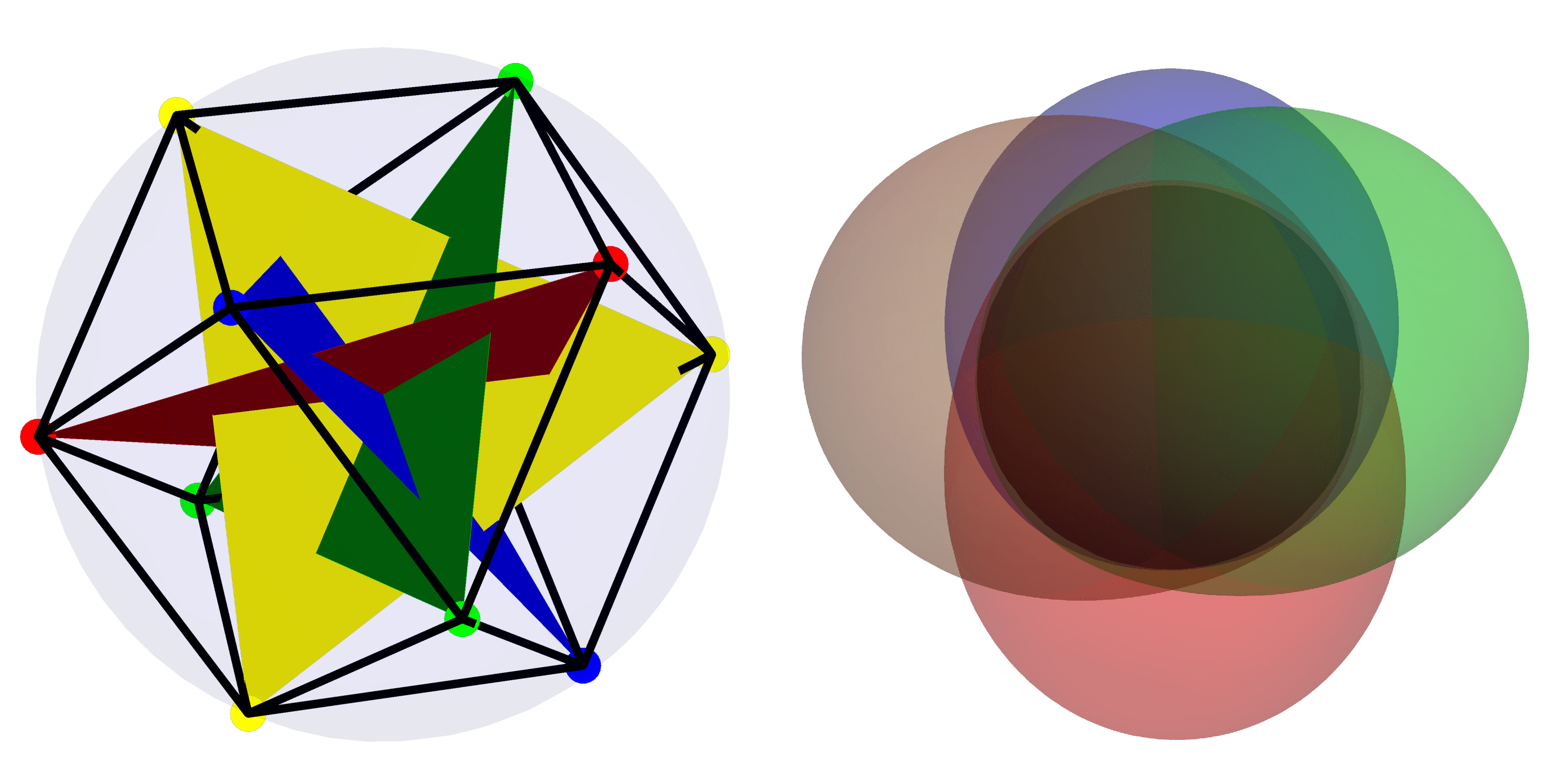
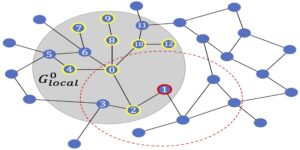
Imagen destacada: en la imagen de la izquierda, la base más "cuántica" en $mathcal{H}_4$ se representa utilizando la representación estelar. A la derecha, se presenta la función Husimi para estados en la base más coherente (“clásica”) dentro de $mathcal{H}_4$.

Resumen popular

Extremal states, coherent and anticoherent, have practical applications in quantum metrology as optimal rotosensors. This work provides a natural extension of previous studies concerning the search for such states proposing optimal orthogonal measurements of Lüders and von Neumann of the extreme spin coherence. We introduce the measure $mathcal{B}_t$ as the tool to characterize the quantumness of a measurement given by a basis in $mathcal{H}_N$. The search for the most quantum bases for $N=3,4,5$ and $7$ is performed. Numerical results suggest, that the obtained solutions are unique. A set of candidates for the “classical” bases consisting of the most spin-coherent states is indicated for $N=3,4,5,6$. Some of the most quantum bases, analyzed in the stellar representation of Majorana, reveal symmetries of Platonic solids. Most classical bases display symmetric structures too. We also considered other measures of the quantumness of vectors forming a given basis. Optimization of the mean Wehrl entropy of $N$ orthogonal vectors leads to the same bases distinguished by extremal values of the quantities $mathcal{B}_t$, with a single exception of the quantum basis for $N=6$.

► datos BibTeX

@article{Rudzinski2024orthonormalbasesof, doi = {10.22331/q-2024-01-25-1234}, url = {https://doi.org/10.22331/q-2024-01-25-1234}, title = {Orthonormal bases of extreme quantumness}, author = {Rudzi{‘{n}}ski, Marcin and Burchardt, Adam and {.{Z}}yczkowski, Karol}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {8}, pages = {1234}, month = jan, year = {2024} }

► referencias

[ 1 ] T. Frankel, La geometría de la física: una introducción, 3.ª ed., Cambridge University Press (2011).
https: / / doi.org/ 10.1017 / CBO9781139061377

[ 2 ] D. Chruściński y A. Jamiołkowski, Fases geométricas en la mecánica clásica y cuántica, Birkhäuser (2004).
https://doi.org/10.1007/978-0-8176-8176-0

[ 3 ] DA Lee, Relatividad geométrica, Sociedad Estadounidense de Matemáticas, Providence (2021).
https: / / doi.org/ 10.1090 / gsm / 201

[ 4 ] I. Bengtsson y K. Życzkowski, Geometría de los estados cuánticos: una introducción al entrelazamiento cuántico, 2ª ed., Cambridge University Press (2017).
https: / / doi.org/ 10.1017 / 9781139207010

[ 5 ] M. Lewin, Métodos geométricos para sistemas cuánticos no lineales de muchos cuerpos, J. Functional Analysis 260, 12, (2011).
https: / / doi.org/ 10.1016 / j.jfa.2010.11.017

[ 6 ] E. Cohen, H. Larocque, F. Bouchard et al., Fase geométrica de Aharonov-Bohm a Pancharatnam-Berry y más allá, Nat. Rev. Phys. 1, 437–449 (2019).
https://doi.org/10.1038/s42254-019-0071-1

[ 7 ] E. Majorana Atomi orientati in campo magnético variable, Nuovo Cimento 9, 43-50 (1932).
https: / / doi.org/ 10.1007 / BF02960953

[ 8 ] R. Barnett, A. Turner y E. Demler, Clasificación de nuevas fases de átomos de espinor, Phys. Rev. Lett. 97, 180412 (2006).
https: / / doi.org/ 10.1103 / PhysRevLett.97.180412

[ 9 ] R. Barnett, A. Turner y E. Demler, Clasificación de vórtices en condensados de Bose-Einstein $ S = 3 $, Phys. Rev. A 76, 013605 (2007).
https: / / doi.org/ 10.1103 / PhysRevA.76.013605

[ 10 ] H. Mäkelä y K.-A. Suominen, Estados inertes de sistemas de espín, Phys. Rev. Lett. 99, 190408 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.190408

[ 11 ] E. Serrano-Ensástiga y F. Mireles, Caracterización de fases de condensados de espinor Bose-Einstein: un enfoque de representación estelar de Majorana, Phys. Letón. A 492, 129188 (2023).
https: / / doi.org/ 10.1016 / j.physleta.2023.129188

[ 12 ] P. Mathonet at al., Equivalencia de entrelazamiento de estados simétricos de $ N $ -qubit, Phys. Rev. A 81, 052315 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.052315

[ 13 ] J. Martin, O. Giraud, PA Braun, D. Braun y T. Bastin, Estados simétricos multiqubit con alto entrelazamiento geométrico, Phys. Rev. A 81, 062347 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.062347

[ 14 ] M. Aulbach, DJH Markham y M. Murao, El estado simétrico máximamente entrelazado en términos de la medida geométrica, New J. Phys. 12, 073025 (2010).
https://doi.org/10.1088/1367-2630/12/7/073025

[ 15 ] DJH Markham, Entrelazamiento y simetría en estados simétricos de permutación, Phys. Rev. A 83, 042332 (2011).
https: / / doi.org/ 10.1103 / PhysRevA.83.042332

[ 16 ] P. Ribeiro y R. Mosseri, Entrelazamiento en el sector simétrico de $n$ qubits, Phys. Rev. Lett. 106, 180502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.106.180502

[ 17 ] M.Aulbach, Clasificación del entrelazamiento en estados simétricos, Int. J. Información cuántica. 10, 1230004 (2012).
https: / / doi.org/ 10.1142 / S0219749912300045

[ 18 ] W. Ganczarek, M. Kuś y K. Życzkowski, Medida baricéntrica del entrelazamiento cuántico, Phys. Rev. A 85, 032314 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.032314

[ 19 ] A. Mandilara, T. Coudreau, A. Keller y P. Milman, Clasificación de entrelazamiento de estados simétricos puros mediante estados coherentes de espín, Phys. Rev.A 90, 050302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.050302

[ 20 ] P. Hyllus, at al., Información de Fisher y entrelazamiento de múltiples partículas, Phys. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[ 21 ] JH Hannay, La fase Berry para girar en la representación de Majorana, J. Phys. R: Matemáticas. Génesis 31, L53 (1998).
https://doi.org/10.1088/0305-4470/31/2/002

[ 22 ] P. Bruno, Fase geométrica cuántica en la representación estelar de Majorana: mapeo de una fase Aharonov-Bohm de muchos cuerpos, Phys. Rev. Lett. 108, 240402 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.240402

[ 23 ] HD Liu y LB Fu, Fase Berry y entrelazamiento cuántico en la representación estelar de Majorana, Phys. Rev. A 94, 022123 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.022123

[ 24 ] P. Ribeiro, J. Vidal y R. Mosseri, Límite termodinámico del modelo Lipkin-Meshkov-Glick, Phys. Rev. Lett. 99, 050402 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.050402

[ 25 ] P. Ribeiro, J. Vidal y R. Mosseri, Espectro exacto del modelo Lipkin-Meshkov-Glick en el límite termodinámico y correcciones de tamaño finito, Phys. Rev.E 78, 021106 (2008).
https: / / doi.org/ 10.1103 / PhysRevE.78.021106

[ 26 ] J. Zimba, Estados de espín “anticoherentes” a través de la representación de Majorana, Electron. J. Theor. Física. 3, 143 (2006).
https:///api.semanticscholar.org/CorpusID:13938120

[ 27 ] D. Baguette, T. Bastin y J. Martin, Estados simétricos de múltiples bits con reducciones de un qubit de mezcla máxima máxima, Phys. Rev. A 90, 032314 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.032314

[ 28 ] O. Giraud, D. Braun, D. Baguette, T. Bastin y J. Martin, representación tensora de estados de espín, Phys. Rev. Lett. 114, 080401 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.080401

[ 29 ] D. Baguette, F. Damanet, O. Giraud y J. Martin, Anticoherencia de estados de espín con simetrías de grupo de puntos, Phys. Rev. A 92, 052333 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.92.052333

[ 30 ] HD Liu, LB Fu, X. Wang, Enfoque de estado coherente para la representación de Majorana, Commun. Teor. Física. 67, 611 (2017).
https://doi.org/10.1088/0253-6102/67/6/611

[ 31 ] D. Baguette y J. Martin, Medidas de anticoherencia para estados de espín puro, Phys. Rev. A 96, 032304 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.032304

[ 32 ] P. Kolenderski y R. Demkowicz-Dobrzański, Estado óptimo para mantener alineados los marcos de referencia y los sólidos platónicos, Phys. Rev. A 78, 052333 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052333

[ 33 ] C. Chryssomalakos y H. Hernández-Coronado, Rotosensores cuánticos óptimos, Phys. Rev. A 95, 052125 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.95.052125

[ 34 ] AZ Goldberg y DFV James, Mediciones de ángulos de Euler cuánticas limitadas utilizando estados anticoherentes, Phys. Rev. A 98, 032113 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032113

[ 35 ] J. Martin, S. Weigert y O. Giraud, Detección óptima de rotaciones alrededor de ejes desconocidos mediante estados coherentes y anticoherentes, Quantum 4, 285 (2020).
https://doi.org/10.22331/q-2020-06-22-285

[ 36 ] J. Crann, DW Kribs y R. Pereira, Diseños esféricos y estados de espín anticoherentes, J. Phys. R: Matemáticas. Teor. 43, 255307 (2010).
https://doi.org/10.1088/1751-8113/43/25/255307

[ 37 ] E. Bannai y M. Tagami, Una nota sobre estados de espín anticoherentes, J. Phys. R: Matemáticas. Teor. 44, 342002 (2011).
https://doi.org/10.1088/1751-8113/44/34/342002

[ 38 ] M. Wang e Y. Zhu, Estados anticoherentes de spin-2 y diseños esféricos, J. Phys. R: Matemáticas. Teor. 55, 425304 (2022).
https:///doi.org/10.1088/1751-8121/ac971d

[ 39 ] AZ Goldberg, AB Klimov, M.Grassl, G. Leuchs y LL Sánchez-Soto, Estados cuánticos extremos, AVS Quantum Sci. 2, 044701 (2020).
https: / / doi.org/ 10.1116 / 5.0025819

[ 40 ] AZ Goldberg, M. Grassl, G. Leuchs y LL Sánchez-Soto, Cuantidad más allá del entrelazamiento: el caso de los estados simétricos, Phys. Rev.A 105, 022433 (2022).
https: / / doi.org/ 10.1103 / PhysRevA.105.022433

[ 41 ] O. Giraud, P. Braun y D. Braun, Cuantificación de la cuántica y la búsqueda de reinas de la cuántica, New J. Phys. 12, 063005 (2010).
https://doi.org/10.1088/1367-2630/12/6/063005

[ 42 ] R. Delbourgo, Estados de incertidumbre mínima para el grupo de rotación y grupos aliados, J. Phys. A 10, L233 (1977).
https://doi.org/10.1088/0305-4470/10/11/012

[ 43 ] A. Wehrl, Sobre la relación entre la entropía clásica y la mecánica cuántica, Rep. Math. Física. 16, 353 (1979).
https://doi.org/10.1016/0034-4877(79)90070-3

[ 44 ] EH Lieb, Prueba de una conjetura de entropía de Wehrl, Commun. Matemáticas. Física. 62, 35 (1978).
https: / / doi.org/ 10.1007 / BF01940328

[ 45 ] CT Lee, la entropía de los estados de espín de Wehrl y la conjetura de Lieb, J. Phys. A 21, 3749 (1988).
https://doi.org/10.1088/0305-4470/21/19/013

[ 46 ] EH Lieb y JP Solovej, Prueba de una conjetura de entropía para estados de espín coherentes de Bloch y sus generalizaciones, Acta Math. 212, 379 (2014).
https://doi.org/10.1007/s11511-014-0113-6

[ 47 ] F. Bouchard, at al., Metrología cuántica en el límite con constelaciones extremas de Majorana, Optica 4, 1429-1432 (2017).
https: / / doi.org/ 10.1364 / OPTICA.4.001429

[ 48 ] A. Wehrl, Propiedades generales de la entropía, Rev. Mod. Física. 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[ 49 ] A. Wehrl, Las múltiples facetas de la entropía, Rep. Math. Física. 30, 119 (1991).
https://doi.org/10.1016/0034-4877(91)90045-O

[ 50 ] S. Gnutzmann y K. Życzkowski, Las entropías de Renyi-Wehrl como medidas de localización en el espacio de fases, J. Phys. A 34, 10123 (2001).
https://doi.org/10.1088/0305-4470/34/47/317

[ 51 ] K. Życzkowski, Localización de estados propios y entropía media de Wehrl, Physica E 9, 583 (2001).
https://doi.org/10.1016/S1386-9477(00)00266-6

[ 52 ] LL Sánchez-Soto, AB Klimov, P. de la Hoz y G. Leuchs, Estados de polarización cuánticos versus clásicos: cuando los multipolos cuentan, J. Phys. B 46 104011 (2013).
https://doi.org/10.1088/0953-4075/46/10/104011

[ 53 ] A. Tavakoli y N. Gisin, Los sólidos platónicos y las pruebas fundamentales de la mecánica cuántica, Quantum 4, 293 (2020).
https://doi.org/10.22331/q-2020-07-09-293

[ 54 ] H.Ch. Nguyen, S. Designolle, M. Barakat y O. Gühne, Simetrías entre mediciones en mecánica cuántica, preimpresión arXiv:2003.12553 (2022).
https:///doi.org/10.48550/arXiv.2003.12553
arXiv: 2003.12553

[ 55 ] JI Latorre y G. Sierra, Enredo platónico, Quantum Inf. Computadora. 21, 1081 (2021).
https: / / doi.org/ 10.26421 / QIC21.13-14-1

[ 56 ] K. Bolonek-Lasoń y P. Kosiński, Grupos, sólidos platónicos y desigualdades de Bell, Quantum 5, 593 (2021).
https://doi.org/10.22331/q-2021-11-29-593

[ 57 ] KF Pál y T. Vértesi, Grupos, Desigualdades de la campana platónica para todas las dimensiones, Quantum 6, 756 (2022).
https://doi.org/10.22331/q-2022-07-07-756

[ 58 ] RH Dicke, Coherencia en procesos de radiación espontánea, Phys. Rev. 93, 99 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99

[ 59 ] V. Karimipour y L. Memarzadeh, Bases equienredadas en dimensiones arbitrarias Phys. Rev. A 73, 012329 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.73.012329

[ 60 ] G. Rajchel, A. Gąsiorowski y K. Życzkowski, Matrices robustas de Hadamard, rayos unistocásticos en politopo de Birkhoff y bases equientrelazadas en espacios compuestos Matemáticas. comp. Ciencia. 12, 473 (2018).
https: / / doi.org/ 10.1007 / s11786-018-0384-y

[ 61 ] J. Czartowski, D. Goyeneche, M. Grassl y K. Życzkowski, Bases isoentrelazadas mutuamente insesgadas, mediciones cuánticas simétricas y diseños de estados mixtos, Phys. Rev. Lett. 124, 090503 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.124.090503

[ 62 ] F. Del Santo, J. Czartowski, K. Życzkowski y N. Gisin, Bases isoentrelazadas y medidas de juntas, preimpresión arXiv:2307.06998 (2023).
https:///doi.org/10.48550/arXiv.2307.06998
arXiv: 2307.06998

[ 63 ] R. Penrose, Sobre la no localidad de Bell sin probabilidades: alguna geometría curiosa, Reflexiones cuánticas (2000).

[ 64 ] J. Zimba y R. Penrose, Sobre la no localidad de Bell sin probabilidades: geometría más curiosa, Stud. Historia. Fil. Ciencia. 24, 697 (1993).
https://doi.org/10.1016/0039-3681(93)90061-N

[ 65 ] JE Massad y PK Aravind, El dodecaedro de Penrose revisitado, Am. J. Física 67, 631 (1999).
https: / / doi.org/ 10.1119 / 1.19336

[ 66 ] K. Husimi, Algunas propiedades formales de la matriz de densidad, Proc. Física. Matemáticas. Soc. 22, 264 (1940).
https: / / doi.org/ 10.11429 / ppmsj1919.22.4_264

[ 67 ] W. Słomczyński y K. Życzkowski, La entropía dinámica media de mapas cuánticos en la esfera diverge en el límite semiclásico, Phys. Rev. Lett. 80, 1880 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.1880

[ 68 ] M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, Transportadores cuánticos perfectos, preimpresión arXiv:2310.13045 (2023).
https:///doi.org/10.48550/arXiv.2310.13045
arXiv: 2310.13045

[ 69 ] NCN Maestro 7 2015/18/A/ST2/00274 sitio web https://chaos.if.uj.edu.pl/ karol/Maestro7/files/data3/Numerical_Results.dat.
https://chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

[ 70 ] D. Weingarten, Comportamiento asintótico de integrales de grupo en el límite de rango infinito, J. Math. Física. 19, 999 (1978).
https: / / doi.org/ 10.1063 / 1.523807

[ 71 ] B. Collins y P. Śniady, Integración con respecto a la medida de Haar en grupos unitarios, ortogonales y simplécticos, Commun. Matemáticas. Física. 264, 773 (2006).
https://doi.org/10.1007/s00220-006-1554-3

[ 72 ] G. Rajchel, Mapeos y diseños cuánticos, tesis doctoral, preimpresión arXiv:2204.13008 (2022).
https:///doi.org/10.48550/arXiv.2204.13008
arXiv: 2204.13008

[ 73 ] D. Martin y EP Wigner, Teoría de grupos y su aplicación a la mecánica cuántica de los espectros atómicos, Academic Press Inc. NY (1959).
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

Citado por

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny y Kamil Korzekwa, “Protractores cuánticos perfectos”, arXiv: 2310.13045, (2023).

[2] Aaron Z. Goldberg, “Correlaciones para subconjuntos de partículas en estados simétricos: qué hacen los fotones dentro de un haz de luz cuando se ignora el resto”, arXiv: 2401.05484, (2024).

Las citas anteriores son de ANUNCIOS SAO / NASA (última actualización exitosa 2024-01-25 11:53:23). La lista puede estar incompleta ya que no todos los editores proporcionan datos de citas adecuados y completos.

No se pudo recuperar Crossref citado por datos durante el último intento 2024-01-25 11:53:22: No se pudieron obtener los datos citados por 10.22331 / q-2024-01-25-1234 de Crossref. Esto es normal si el DOI se registró recientemente.

Este documento se publica en Quantum bajo el Creative Commons Reconocimiento 4.0 Internacional (CC BY 4.0) licencia. Los derechos de autor permanecen con los titulares de derechos de autor originales, como los autores o sus instituciones.

Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
PlatoData.Network Vertical Generativo Ai. Empodérate. Accede Aquí.
PlatoAiStream. Inteligencia Web3. Conocimiento amplificado. Accede Aquí.
PlatoESG. Carbón, tecnología limpia, Energía, Ambiente, Solar, Gestión de residuos. Accede Aquí.
PlatoSalud. Inteligencia en Biotecnología y Ensayos Clínicos. Accede Aquí.
Fuente: https://quantum-journal.org/papers/q-2024-01-25-1234/

Sello de tiempo: Enero 25, 2024

Sello de tiempo: 11 de jul, 2023

Bases ortonormales de cuántica extrema.

Reeditado por Platón

Resumen

Resumen popular

► datos BibTeX

► referencias

Citado por

Mas de Diario cuántico

Búsqueda local cuántica con el operador alterno cuántico Ansatz

Algoritmo de descomposición de dos unidades y simulación de sistema cuántico abierto

Simulación de circuitos cuánticos utilizando redes de tensor de árbol

Experimentos de estabilidad: el doble pasado por alto de los experimentos de memoria

Retroalimentación coherente en sistemas optomecánicos en el régimen de banda lateral no resuelta

Distribución experimental de claves semicuánticas con usuarios clásicos

Redes antagónicas generativas cuánticas basadas en estilos para eventos de Monte Carlo

Diseños de estados cuánticos emergentes y biunitaridad en dinámica de circuitos duales unitarios

Diagnóstico de mesetas estériles con herramientas de Quantum Optimal Control

Límite de velocidad cuántica del operador geométrico, flujo hamiltoniano de Wegner y crecimiento del operador

Sobre Nosotros

Búsqueda vertical y Ai

Productos

Manténganse Conectados

Mi Cuenta