Explicación del bayesiano ingenuo gaussiano

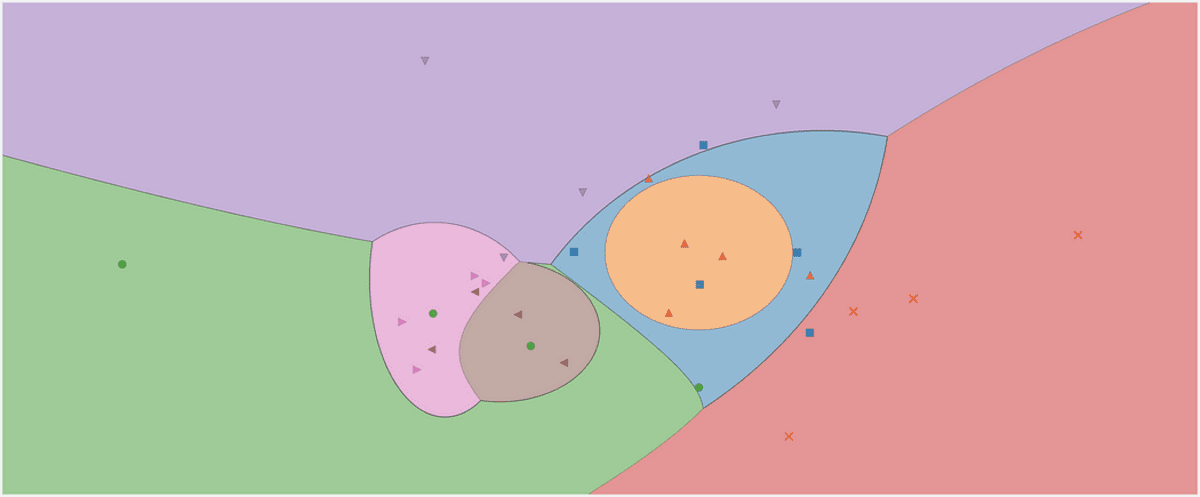
La región de decisión de un clasificador bayesiano ingenuo gaussiano. Imagen del autor.

Creo que este es un clásico al comienzo de cada carrera de ciencia de datos: el Clasificador ingenuo de Bayes. O debería decir más bien el familia de clasificadores de Bayes ingenuos, ya que vienen en muchos sabores. Por ejemplo, hay un clasificador Naive Bayes multinomial, un Bernoulli Naive Bayes y también un clasificador Gaussiano Naive Bayes, cada uno diferente en solo un pequeño detalle, como veremos. Los algoritmos ingenuos de Bayes tienen un diseño bastante simple, pero resultaron útiles en muchas situaciones complejas del mundo real.

En este artículo, puede aprender

• cómo funcionan los clasificadores ingenuos de Bayes,
• por qué tiene sentido definirlos como son y
• cómo implementarlos en Python usando NumPy.

Puedes encontrar el código en mi Github.

Podría ayudar un poco revisar mi manual sobre estadísticas bayesianas Una suave introducción a la inferencia bayesiana acostumbrarse a la fórmula de Bayes. Como implementaremos el clasificador en una forma de conformidad de aprendizaje de scikit, también vale la pena consultar mi artículo Cree su propia regresión de scikit-learn personalizada. Sin embargo, la sobrecarga de scikit-learn es bastante pequeña y debería poder seguirlo de todos modos.

Comenzaremos explorando la teoría asombrosamente simple de la ingenua clasificación de Bayes y luego pasaremos a la implementación.

¿Qué nos interesa realmente a la hora de clasificar? ¿Qué estamos haciendo realmente, cuál es la entrada y la salida? La respuesta es simple:

Dado un punto de datos x, ¿cuál es la probabilidad de que x pertenezca a alguna clase c?

Eso es todo lo que queremos responder con cualquier clasificación. Puede modelar directamente esta declaración como una probabilidad condicional: p(c|x).

Por ejemplo, si hay

• clases 3 c₁, c₂, c₃y
• x consta de 2 caracteristicas x₁, x₂,

el resultado de un clasificador podría ser algo como p(c₁|x₁, x₂) = 0.3, p(c₂|x₁, x₂)=0.5 y p(c₃|x₁, x₂)=0.2. Si nos preocupamos por una sola etiqueta como salida, elegiríamos la de mayor probabilidad, es decir c₂ con una probabilidad del 50% aquí.

El clasificador ingenuo de Bayes intenta calcular estas probabilidades directamente.

Bayes ingenuos

Ok, dado un punto de datos x, queremos calcular p(c|x) para todas las clases c y luego generar el c con la mayor probabilidad. En las fórmulas a menudo ves esto como

Imagen del autor.

Nota:  max p(c|x) devuelve la máxima probabilidad mientras que argmax p(c|x) devuelve el c con esta máxima probabilidad.

Pero antes de que podamos optimizar p(c|x), tenemos que ser capaces de calcularlo. Para esto, usamos Teorema de Bayes:

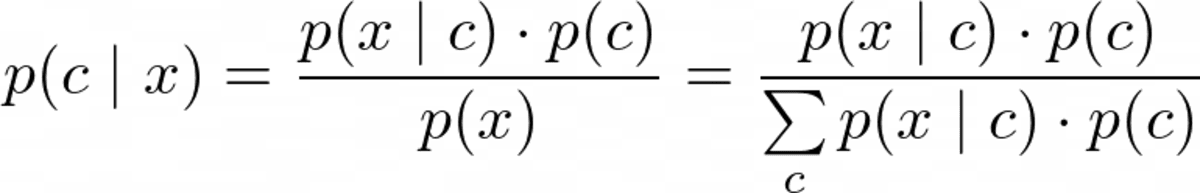
Teorema de Bayes. Imagen del autor.

Esta es la parte bayesiana de naive bayes. Pero ahora, tenemos el siguiente problema: ¿Cuáles son p(x|c) y p(c)?

De esto se trata el entrenamiento de un clasificador bayesiano ingenuo.

El entrenamiento

Para ilustrar todo, usemos un conjunto de datos de juguete con dos características reales x₁, x₂y tres clases c₁, c₂, c₃ en lo siguiente.

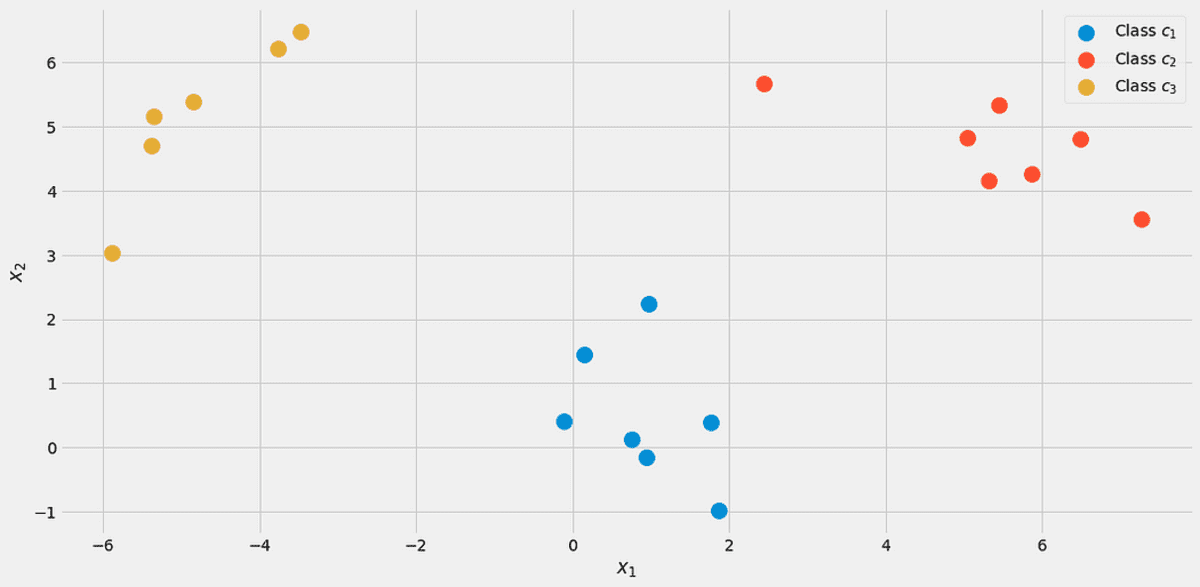
Los datos, visualizados. Imagen del autor.

Puede crear este conjunto de datos exacto a través de

from sklearn.datasets import make_blobs X, y = make_blobs(n_samples=20, centers=[(0,0), (5,5), (-5, 5)], random_state=0)

Empecemos por el probabilidad de clase p(c), la probabilidad de que alguna clase c se observa en el conjunto de datos etiquetado. La forma más sencilla de estimar esto es simplemente calcular las frecuencias relativas de las clases y usarlas como probabilidades. Podemos usar nuestro conjunto de datos para ver qué significa esto exactamente.

Hay 7 de 20 puntos etiquetados como clase c₁ (azul) en el conjunto de datos, por lo tanto decimos p(c₁)=7/20. Tenemos 7 puntos por clase. c₂ (rojo) también, por lo tanto establecemos p(c₂)=7/20. La última clase c₃ (amarillo) tiene solo 6 puntos, por lo tanto p(c₃)=6/20.

Este simple cálculo de las probabilidades de clase se asemeja a un enfoque de máxima verosimilitud. Sin embargo, también puede utilizar otro antes distribución, si lo desea. Por ejemplo, si sabe que este conjunto de datos no es representativo de la verdadera población porque la clase c₃ debe aparecer en el 50% de los casos, luego configura p(c₁) = 0.25, p(c₂)=0.25 y p(c₃)=0.5. Cualquier cosa que le ayude a mejorar el rendimiento en el conjunto de prueba.

Ahora nos dirigimos a la probabilidad p(x|c)=p(x₁, x₂|c). Un enfoque para calcular esta probabilidad es filtrar el conjunto de datos para muestras con etiqueta c y luego intente encontrar una distribución (por ejemplo, una gaussiana bidimensional) que capture las características x₁, x₂.

Desafortunadamente, por lo general, no tenemos suficientes muestras por clase para hacer una estimación adecuada de la probabilidad.

Para poder construir un modelo más robusto, hacemos el suposición ingenua que las caracteristicas x₁, x₂ en estocásticamente independientedado c. Esta es solo una forma elegante de hacer que las matemáticas sean más fáciles a través de

Imagen del autor

para cada clase c. Aquí es donde el ingenuo parte de Naive Bayes proviene de que esta ecuación no se cumple en general. Aún así, incluso entonces, el ingenuo Bayes produce buenos resultados, a veces sobresalientes en la práctica. Especialmente para problemas de PNL con características de bolsa de palabras, brilla el ingenuo Bayes multinomial.

Los argumentos dados anteriormente son los mismos para cualquier clasificador de Bayes ingenuo que pueda encontrar. Ahora solo depende de cómo modeles p(x₁|c₁), p(x₂|c₁), p(x₁|c₂), p(x₂|c₂), p(x₁|c₃) y p(x₂|c₃).

Si sus características son 0 y 1 solamente, podría usar un Distribución de Bernoulli. Si son números enteros, un Distribución multinomial. Sin embargo, tenemos valores de características reales y decidimos por un Gauss distribución, de ahí el nombre Gaussian naive Bayes. Asumimos la siguiente forma

Imagen del autor.

donde µᵢ,ⱼ es la media y σᵢ,ⱼ es la desviación estándar que tenemos que estimar a partir de los datos. Esto significa que obtenemos una media para cada característica. i junto con una clase cⱼ, en nuestro caso 2*3=6 significa. Lo mismo ocurre con las desviaciones estándar. Esto requiere un ejemplo.

Tratemos de estimar μ₂,₁ y σ₂,₁. Porque j=1, solo nos interesa la clase c₁, solo conservemos muestras con esta etiqueta. Quedan las siguientes muestras:

# samples with label = c_1 array([[ 0.14404357, 1.45427351], [ 0.97873798, 2.2408932 ], [ 1.86755799, -0.97727788], [ 1.76405235, 0.40015721], [ 0.76103773, 0.12167502], [-0.10321885, 0.4105985 ], [ 0.95008842, -0.15135721]])

Ahora, debido a i=2 solo tenemos que considerar la segunda columna. μ₂,₁ es la media y σ₂,₁ la desviación estándar de esta columna, es decir μ₂,₁ = 0.49985176 y σ₂,₁ = 0.9789976.

Estos números tienen sentido si vuelves a mirar el diagrama de dispersión desde arriba. Las características x₂ de las muestras de la clase c₁ son alrededor de 0.5, como se puede ver en la imagen.

Calculamos esto ahora para las otras cinco combinaciones y ¡hemos terminado!

En Python, puedes hacerlo así:

from sklearn.datasets import make_blobs
import numpy as np # Create the data. The classes are c_1=0, c_2=1 and c_3=2.
X, y = make_blobs( n_samples=20, centers=[(0, 0), (5, 5), (-5, 5)], random_state=0
) # The class probabilities.
# np.bincounts counts the occurence of each label.
prior = np.bincount(y) / len(y) # np.where(y==i) returns all indices where the y==i.
# This is the filtering step.
means = np.array([X[np.where(y == i)].mean(axis=0) for i in range(3)])
stds = np.array([X[np.where(y == i)].std(axis=0) for i in range(3)])

Recibimos

# priors
array([0.35, 0.35, 0.3 ])
# means array([[ 0.90889988, 0.49985176], [ 5.4111385 , 4.6491892 ], [-4.7841679 , 5.15385848]])
# stds
array([[0.6853714 , 0.9789976 ], [1.40218915, 0.67078568], [0.88192625, 1.12879666]])

Este es el resultado del entrenamiento de un clasificador bayesiano ingenuo gaussiano.

Haciendo predicciones

La fórmula de predicción completa es

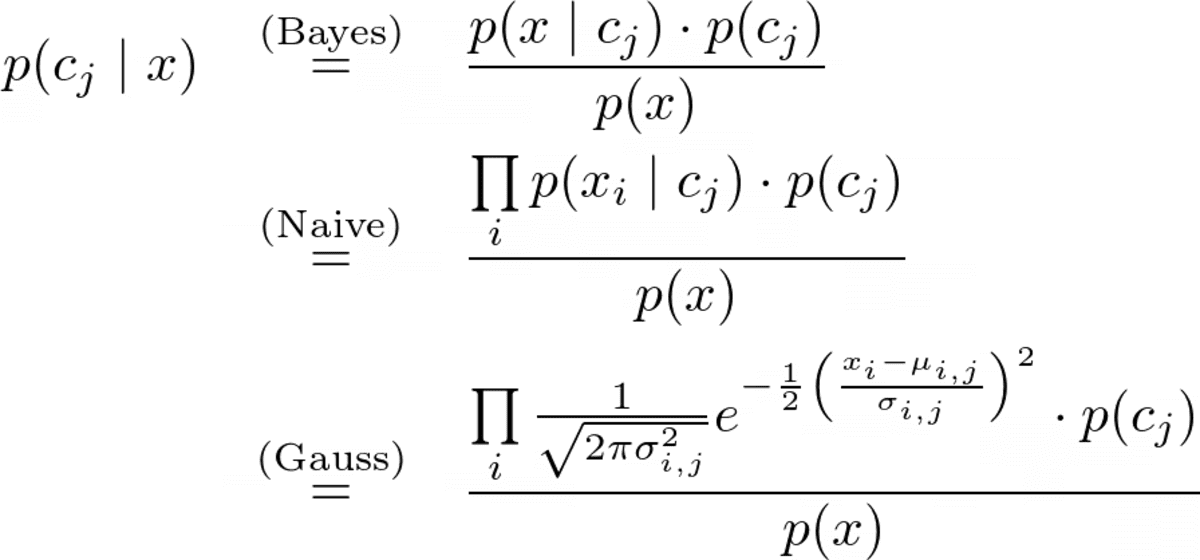
Imagen del autor.

Supongamos un nuevo punto de datos x*=(-2, 5) entra.

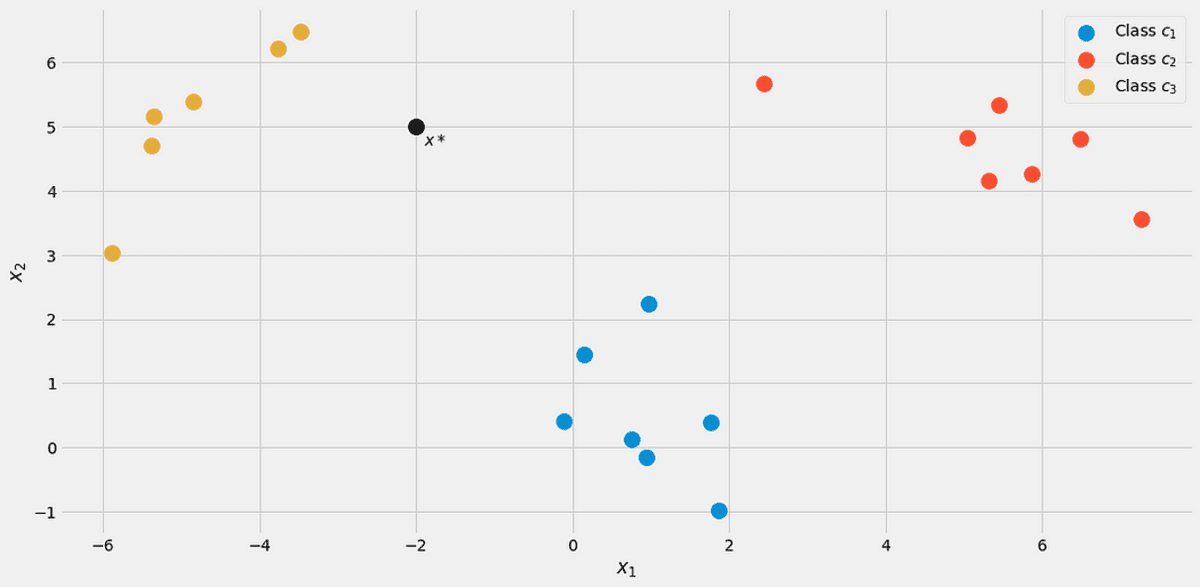
Imagen del autor.

Para ver a qué clase pertenece, calculemos p(c|x*) para todas las clases. De la imagen, debería pertenecer a la clase. c₃ = 2, pero vamos a ver. Ignoremos el denominador p(x) por un segundo. Usando el siguiente bucle calculó los nominadores para j = 1, 2, 3.

x_new = np.array([-2, 5]) for j in range(3): print( f"Probability for class {j}: {(1/np.sqrt(2*np.pi*stds[j]**2)*np.exp(-0.5*((x_new-means[j])/stds[j])**2)).prod()*p[j]:.12f}" )

Recibimos

Probability for class 0: 0.000000000263
Probability for class 1: 0.000000044359
Probability for class 2: 0.000325643718

Por supuesto, estos probabilidades (no deberíamos llamarlos así) no sumen uno ya que ignoramos el denominador. Sin embargo, esto no es un problema ya que podemos simplemente tomar estas probabilidades no normalizadas y dividirlas por su suma, luego sumarán uno. Entonces, dividiendo estos tres valores por su suma de aproximadamente 0.00032569, obtenemos

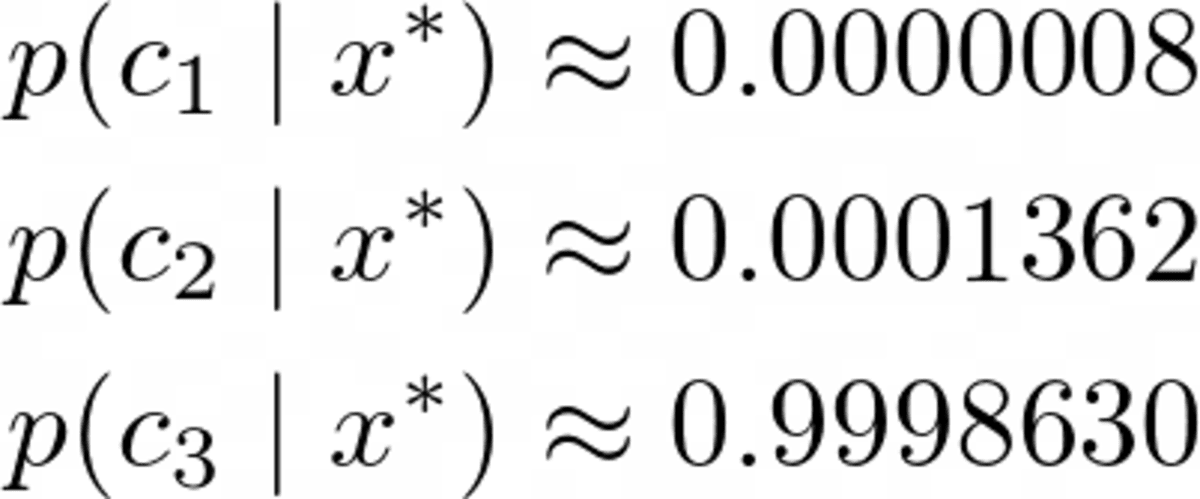
Imagen del autor.

Un claro ganador, como esperábamos. Ahora, ¡vamos a implementarlo!

Esta implementación es, con mucho, poco eficiente, no es numéricamente estable, solo tiene un propósito educativo. Hemos discutido la mayoría de las cosas, por lo que debería ser fácil de seguir ahora. Puedes ignorar todos los check funciones, o leer mi artículo Cree su propio scikit-learn personalizado si estás interesado en lo que hacen exactamente.

Solo tenga en cuenta que implementé un predict_proba método primero para calcular probabilidades. El método predict simplemente llama a este método y devuelve el índice (=clase) con la mayor probabilidad usando una función argmax (¡ahí está de nuevo!). La clase espera clases de 0 a k-1, donde k es el número de clases.

import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted class GaussianNaiveBayesClassifier(BaseEstimator, ClassifierMixin): def fit(self, X, y): X, y = check_X_y(X, y) self.priors_ = np.bincount(y) / len(y) self.n_classes_ = np.max(y) + 1 self.means_ = np.array( [X[np.where(y == i)].mean(axis=0) for i in range(self.n_classes_)] ) self.stds_ = np.array( [X[np.where(y == i)].std(axis=0) for i in range(self.n_classes_)] ) return self def predict_proba(self, X): check_is_fitted(self) X = check_array(X) res = [] for i in range(len(X)): probas = [] for j in range(self.n_classes_): probas.append( ( 1 / np.sqrt(2 * np.pi * self.stds_[j] ** 2) * np.exp(-0.5 * ((X[i] - self.means_[j]) / self.stds_[j]) ** 2) ).prod() * self.priors_[j] ) probas = np.array(probas) res.append(probas / probas.sum()) return np.array(res) def predict(self, X): check_is_fitted(self) X = check_array(X) res = self.predict_proba(X) return res.argmax(axis=1)

Prueba de la implementación

Si bien el código es bastante corto, todavía es demasiado largo para estar completamente seguros de que no cometimos ningún error. Por lo tanto, vamos a comprobar cómo le va en comparación con el clasificador scikit-learn GaussianNB.

my_gauss = GaussianNaiveBayesClassifier()
my_gauss.fit(X, y)
my_gauss.predict_proba([[-2, 5], [0,0], [6, -0.3]])

salidas

array([[8.06313823e-07, 1.36201957e-04, 9.99862992e-01], [1.00000000e+00, 4.23258691e-14, 1.92051255e-11], [4.30879705e-01, 5.69120295e-01, 9.66618838e-27]])

Las predicciones usando el predict el método son

# my_gauss.predict([[-2, 5], [0,0], [6, -0.3]])
array([2, 0, 1])

Ahora, usemos scikit-learn. Lanzando algo de código

from sklearn.naive_bayes import GaussianNB gnb = GaussianNB()
gnb.fit(X, y)
gnb.predict_proba([[-2, 5], [0,0], [6, -0.3]])

los rendimientos

array([[8.06314158e-07, 1.36201959e-04, 9.99862992e-01], [1.00000000e+00, 4.23259111e-14, 1.92051343e-11], [4.30879698e-01, 5.69120302e-01, 9.66619630e-27]])

Los números se parecen un poco a los de nuestro clasificador, pero están un poco fuera de lugar en los últimos dígitos que se muestran. ¿Hicimos algo mal? No. La versión de scikit-learn simplemente usa otro hiperparámetro var_smoothing=1e-09 . Si configuramos este en cero, obtenemos exactamente nuestros números. ¡Perfecto!

Eche un vistazo a las regiones de decisión de nuestro clasificador. También marqué los tres puntos que usamos para la prueba. Ese punto cercano a la frontera tiene solo un 56.9% de posibilidades de pertenecer a la clase roja, como puede ver en la predict_proba salidas. Los otros dos puntos se clasifican con una confianza mucho mayor.

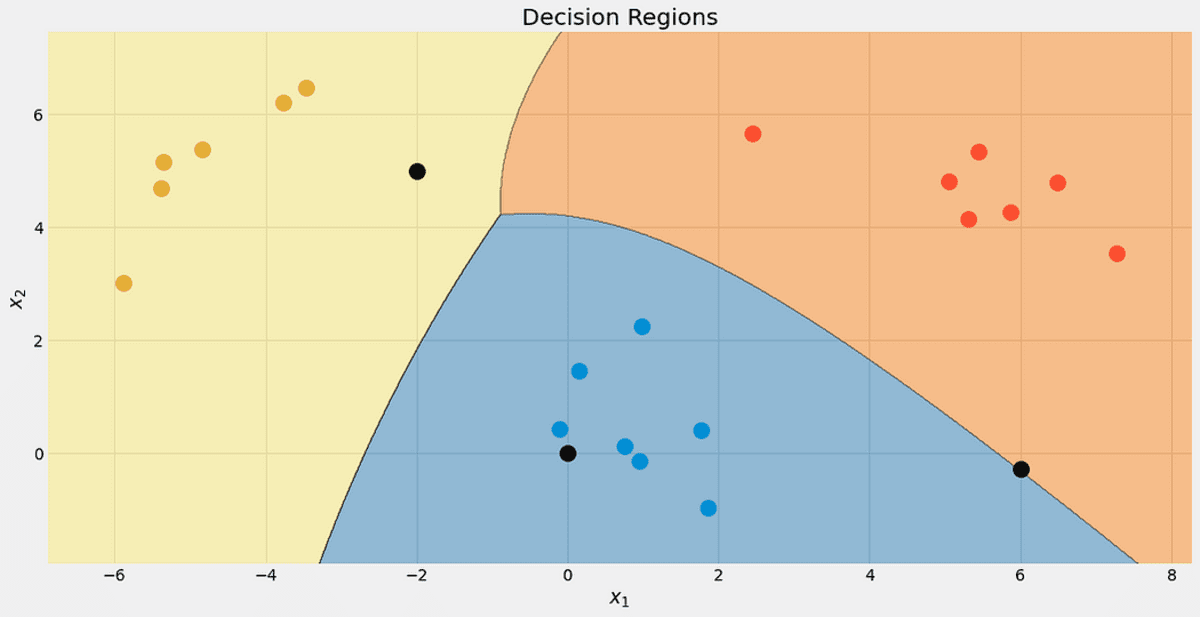
La decisión regiones con los 3 nuevos puntos. Imagen del autor.

En este artículo, aprendimos cómo funciona el clasificador bayesiano ingenuo gaussiano y dimos una intuición de por qué se diseñó de esa manera: es un enfoque directo para modelar la probabilidad de interés. Compare esto con la regresión logística: allí, la probabilidad se modela utilizando una función lineal con una función sigmoidea aplicada encima. Sigue siendo un modelo fácil, pero no se siente tan natural como un clasificador de Bayes ingenuo.

Continuamos calculando algunos ejemplos y recopilando algunas piezas de código útiles en el camino. Finalmente, hemos implementado un clasificador bayesiano ingenuo gaussiano completo de una manera que funciona bien con scikit-learn. Eso significa que puede usarlo en tuberías o búsqueda de cuadrícula, por ejemplo.

Al final, hicimos una pequeña verificación de cordura al importar el propio clasificador ingenuo bayesiano gaussiano de scikit-learns y probar si ambos, nuestro clasificador y el de scikit-learn, arrojan el mismo resultado. Esta prueba fue exitosa.

 
 
Dr. Robert Kübler es científico de datos en Publicis Media y autor en Towards Data Science.

 
Original. Publicado de nuevo con permiso.
 

• Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
• Platoblockchain. Inteligencia del Metaverso Web3. Conocimiento amplificado. Accede Aquí.
• Fuente: https://www.kdnuggets.com/2023/03/gaussian-naive-bayes-explained.html?utm_source=rss&utm_medium=rss&utm_campaign=gaussian-naive-bayes-explained