Quanten-Wasserstein-Abstand basierend auf einer Optimierung über trennbare Zustände

Quanten-Wasserstein-Abstand basierend auf einer Optimierung über trennbare Zustände

Zeitstempel: 16. Oktober 2023, 10:35 Uhr
Quellknoten: 2938953

Géza Toth1,2,3,4,5 und József Pitrik5,6,7

1Theoretische Physik, Universität des Baskenlandes UPV/EHU, ES-48080 Bilbao, Spanien
2EHU Quantum Center, Universität des Baskenlandes UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biskaya, Spanien
3Donostia International Physics Center (DIPC), ES-20080 San Sebastián, Spanien
4IKERBASQUE, Baskische Stiftung für Wissenschaft, ES-48011 Bilbao, Spanien
5Institut für Festkörperphysik und Optik, Wigner Research Center for Physics, HU-1525 Budapest, Ungarn
6Alfréd Rényi Institut für Mathematik, Reáltanoda u. 13-15., HU-1053 Budapest, Ungarn
7Abteilung für Analyse und Operations Research, Institut für Mathematik, Technische und Wirtschaftswissenschaftliche Universität Budapest, Müegyetem rkp. 3., HU-1111 Budapest, Ungarn

Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.

Abstrakt

Wir definieren den Quanten-Wasserstein-Abstand so, dass die Optimierung der Kopplung über bipartite trennbare Zustände und nicht über bipartite Quantenzustände im Allgemeinen durchgeführt wird, und untersuchen seine Eigenschaften. Überraschenderweise stellen wir fest, dass der Selbstabstand mit der Quanten-Fisher-Information zusammenhängt. Wir präsentieren eine Transportkarte, die einem optimalen zweiteiligen trennbaren Zustand entspricht. Wir diskutieren, wie der eingeführte Quanten-Wasserstein-Abstand mit Kriterien zur Erkennung der Quantenverschränkung zusammenhängt. Wir definieren varianzähnliche Größen, die aus der Quanten-Wasserstein-Distanz erhalten werden können, indem wir die Minimierung über Quantenzustände durch eine Maximierung ersetzen. Wir erweitern unsere Ergebnisse auf eine Familie verallgemeinerter Quanten-Fisher-Informationsgrößen.

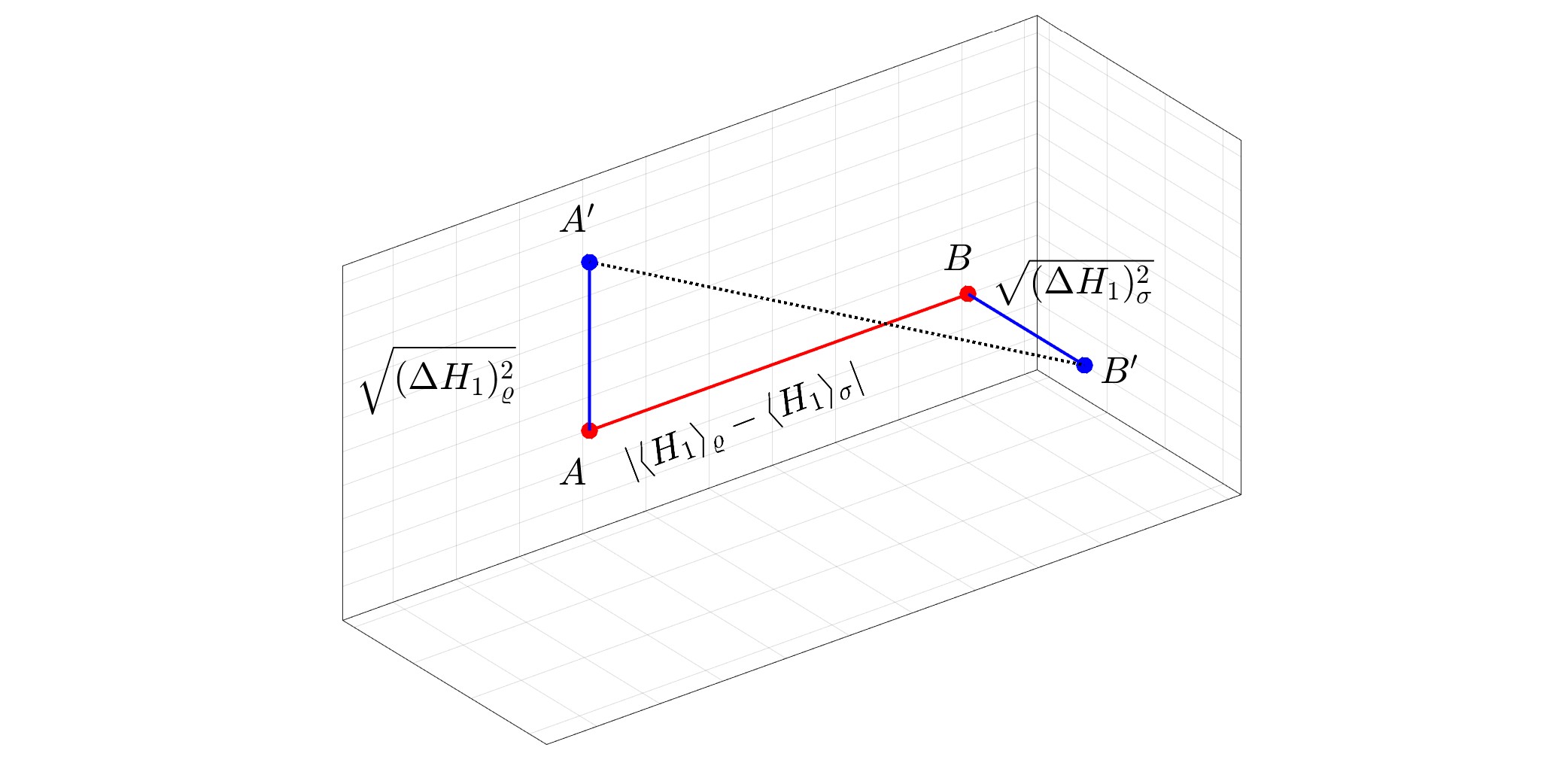
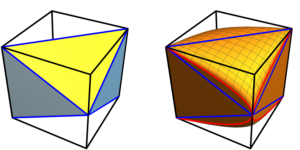
Ausgewähltes Bild: Geometrische Darstellung des Quanten-Wasserstein-Abstands zwischen einem reinen Zustand $varrho$ und einem gemischten Zustand $sigma$ für $N=1.$ Der Quanten-Wasserstein-Abstand entspricht $1/sqrt2$ mal dem üblichen euklidischen Abstand zwischen $A'$ und $B'.$

Populäre Zusammenfassung

Im Alltag sagt uns die Entfernung zweier Städte, wie viele Kilometer wir von einer zur anderen fahren müssen. Es ist auch möglich zu charakterisieren, wie leicht wir von einer Stadt in die andere gelangen können, indem wir den Kraftstoffverbrauch während unserer Fahrt messen. Letzteres ist insofern aussagekräftiger, als es die Reisekosten im Zusammenhang mit der Topographie der Straße widerspiegelt, also empfindlich auf die zugrunde liegende Metrik reagiert. Stellen wir uns als nächstes vor, dass wir einen Sandhaufen von einem Ort zum anderen bewegen müssen und der neue Haufen möglicherweise eine andere Form hat. Auch in diesem Fall können wir den Aufwand für die Sandbeförderung durch die Transportkosten charakterisieren.

Entfernungen spielen in Mathematik, Physik und Ingenieurwissenschaften eine zentrale Rolle. Ein grundlegendes Problem in der Wahrscheinlichkeitsrechnung und Statistik besteht darin, nützliche Maße für den Abstand zwischen zwei Wahrscheinlichkeitsverteilungen zu finden. Leider sind viele Vorstellungen über den Abstand zwischen Wahrscheinlichkeitsverteilungen, beispielsweise p(x) und q(x), maximal, wenn sie sich nicht überlappen, dh eine ist immer Null, wenn die andere ungleich Null ist. Dies ist für viele Anwendungen unpraktisch. Um zum Beispiel auf die Sandanalogie zurückzukommen: Zwei sich nicht überlappende Sandhaufen scheinen gleich weit voneinander entfernt zu sein, unabhängig davon, ob ihr Abstand 10 km oder 100 km beträgt. Die optimale Transporttheorie ist eine Möglichkeit, einen alternativen Begriff des Abstands zwischen Wahrscheinlichkeitsverteilungen zu konstruieren, den sogenannten Wasserstein-Abstand. Sie kann nicht maximal sein, selbst wenn sich die Verteilungen nicht überlappen, sie reagiert empfindlich auf die zugrunde liegende Metrik (d. h. die Kosten des Transports) und im Wesentlichen drückt sie den Aufwand aus, den wir benötigen, um eine zur anderen zu bewegen. als wären es Sandhügel.

Kürzlich wurde der Quanten-Wasserstein-Abstand definiert, indem er den klassischen Wasserstein-Abstand verallgemeinert. Es basiert auf der Minimierung einer Kostenfunktion über den Quantenzuständen eines zweiteiligen Quantensystems. Es hat die Eigenschaft, die der oben erwähnten in der Quantenwelt analog ist. Für orthogonale Zustände kann es nicht maximal sein, was beispielsweise nützlich ist, wenn wir einem Algorithmus Quantendaten beibringen müssen.

Wie zu erwarten ist, weist auch die Quanten-Wasserstein-Distanz Eigenschaften auf, die sich stark von denen ihres klassischen Gegenstücks unterscheiden. Wenn wir beispielsweise den Abstand eines Quantenzustands von sich selbst messen, kann dieser ungleich Null sein. Obwohl dies bereits rätselhaft ist, wurde auch festgestellt, dass der Selbstabstand mit der Wigner-Yanase-Skew-Information zusammenhängt, die 1963 vom Nobelpreisträger EP Wigner eingeführt wurde, der wichtige Beiträge zu den Grundlagen der Quantenphysik und MM Yanase geleistet hat.

In unserer Arbeit betrachten wir diesen mysteriösen Befund aus einer noch anderen Richtung. Wir beschränken die oben erwähnte Minimierung auf sogenannte separierbare Zustände. Dies sind die Quantenzustände, die keine Verschränkung enthalten. Wir stellen fest, dass der Selbstabstand zur Quanten-Fisher-Information wird, einer zentralen Größe in der Quantenmetrologie und der Quantenschätztheorie, die beispielsweise in der berühmten Cramer-Rao-Grenze vorkommt. Durch die Untersuchung der Eigenschaften eines solchen Wasserstein-Abstands ebnet unsere Arbeit den Weg, die Theorie des Quanten-Wasserstein-Abstands mit der Theorie der Quantenverschränkung zu verbinden.

► BibTeX-Daten

► Referenzen

[1] G. Monge. „Mémoire sur la théory des déblais et des remblais“. Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L. Kantorovitch. „Über die Verlagerung von Massen“. Management Science 5, 1–4 (1958). URL: http://www.jstor.org/​stable/​2626967.
http: // www.jstor.org/stable/2626967

[3] Emmanuel Boissard, Thibaut Le Gouic und Jean-Michel Loubes. „Vorlagenschätzung der Distribution mit Wasserstein-Metriken“. Bernoulli 21, 740–759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

[4] Oleg Butkowski. „Subgeometrische Konvergenzraten von Markov-Prozessen in der Wasserstein-Metrik“. Ann. Appl. Wahrscheinlich. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[5] M. Hairer, J.-C. Mattingly und M. Scheutzow. „Asymptotische Kopplung und eine allgemeine Form des Satzes von Harris mit Anwendungen auf stochastische Verzögerungsgleichungen“. Wahrscheinlich. Theorie Bez. Felder 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[6] M. Hairer und JC Mattingly. „Spektrale Lücken in Wasserstein-Entfernungen und die 2D-stochastischen Navier-Stokes-Gleichungen“. Ann. Wahrscheinlich. 36, 2050–2091 (2008).
https://​/​doi.org/​10.1214/​08-AOP392

[7] A. Figalli, F. Maggi und A. Pratelli. „Ein Massentransportansatz für quantitative isoperimetrische Ungleichungen“. Erfinden. Mathematik. 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli und F. Maggi. „Über die Form von Flüssigkeitstropfen und Kristallen im Kleinmassenbereich“. Bogen. Ration. Mech. Anal. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[9] J. Lott und C. Villani. „Ricci-Krümmung für metrische Räume durch optimalen Transport“. Ann. der Mathematik. 169 (3), 903–991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

[10] Max-K. von Renesse und Karl-Theodor Sturm. „Transportungleichungen, Gradientenschätzungen, Entropie und Ricci-Krümmung“. Komm. Reine Appl. Mathematik. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[11] Karl-Theodor Sturm. „Zur Geometrie metrischer Maßräume I“. Acta Math. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[12] Karl-Theodor Sturm. „Zur Geometrie metrischer Maßräume II“. Acta Math. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[13] Benoî̂t Kloeckner. „Eine geometrische Studie von Wassersteinräumen: Euklidische Räume“. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https://doi.org/ 10.2422/2036-2145.2010.2.03

[14] György Pál Gehér, Tamás Titkos und Dániel Virosztek. „Über isometrische Einbettungen von Wassersteinräumen – der diskrete Fall“. J. Mathe. Anal. Appl. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. „Isometrische Untersuchung von Wassersteinräumen – die wahre Linie“. Trans. Amer. Mathematik. Soc. 373, 5855–5883 (2020).
https://​/​doi.org/​10.1090/​tran/​8113

[16] György Pál Gehér, Tamás Titkos und Dániel Virosztek. „Die Isometriegruppe der Wassersteinräume: der Hilbertsche Fall“. J. London. Mathematik. Soc. 106, 3865–3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

[17] György Pál Gehér, Tamás Titkos und Dániel Virosztek. „Isometrische Steifigkeit von Wasserstein-Tori und -Kugeln“. Mathematika 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[18] Gergely Kiss und Tamás Titkos. „Isometrische Steifigkeit von Wassersteinräumen: Der Fall der Graphenmetrik“. Proz. Bin. Mathematik. Soc. 150, 4083–4097 (2022).
https://​/​doi.org/​10.1090/​proc/​15977

[19] György Pál Gehér, Tamás Titkos und Dániel Virosztek. „Über den exotischen Isometriefluss des quadratischen Wassersteinraums über der realen Linie“. Lineare Algebra-Appl. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, SR Park und GK Rohde. „Die kumulative Radon-Verteilungstransformation und ihre Anwendung auf die Bildklassifizierung“. IEEE Trans. Bildprozess. 25, 920–934 (2016).
https://​/​doi.org/​10.1109/​TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek und GK Rohde. „Ein linearer optimaler Transportrahmen zur Quantifizierung und Visualisierung von Variationen in Bildsätzen“. Int. J. Comput. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. „Optimaler Massentransport: Signalverarbeitung und maschinelle Lernanwendungen“. IEEE Signal Processing Magazine 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

[23] A. Gramfort, G. Peyré und M. Cuturi. „Schnelle optimale Transportmittelung von Neuroimaging-Daten“. Informationsverarbeitung in der medizinischen Bildgebung. IPMI 2015. Vorlesungsunterlagen in Informatik 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu und X. Gu. „Formklassifizierung mithilfe der Wasserstein-Distanz zur Analyse der Gehirnmorphometrie“. Informationsverarbeitung in der medizinischen Bildgebung. IPMI 2015. Vorlesungsunterlagen in Informatik 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala und Léon Bottou. „Wasserstein generative gegnerische Netzwerke“. In Doina Precup und Yee Whye Teh, Herausgeber, Proceedings of the 34th International Conference on Machine Learning. Band 70 der Proceedings of Machine Learning Research, Seiten 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] TA El Moselhy und YM Marzouk. „Bayesianische Inferenz mit optimalen Karten“. J. Comput. Physik. 231, 7815–7850 (2012).
https: // doi.org/ 10.1016 / j.jcp.2012.07.022

[27] Gabriel Peyré und Marco Cuturi. „Computergestützter optimaler Transport: mit Anwendungen in der Datenwissenschaft“. Gefunden. Trends maschinelles Lernen. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya und Tomaso A Poggio. „Lernen mit einem Wasserstein-Verlust“. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama und R. Garnett, Herausgeber, Advances in Neural Information Processing Systems. Band 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[29] A. Ramdas, NG Trillos und M. Cuturi. „Über Wasserstein-Tests bei zwei Stichproben und verwandte Familien nichtparametrischer Tests“. Entropy 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[30] S. Srivastava, C. Li und DB Dunson. „Skalierbare Bayes über Barycenter im Wassersteinraum“. J. Mach. Lernen. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski und Wojeciech Slomczynski. „Der Monge-Abstand zwischen Quantenzuständen“. J. Phys. A: Mathe. Gen. 31, 9095–9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[32] Karol Życzkowski und Wojciech Slomczynski. „Die Monge-Metrik zur Sphäre und Geometrie von Quantenzuständen“. J. Phys. A: Mathe. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[33] Ingemar Bengtsson und Karol Życzkowski. „Geometrie von Quantenzuständen: Eine Einführung in die Quantenverschränkung“. Cambridge University Press. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane und D. Voiculescu. „Ein freies Wahrscheinlichkeitsanalogon der Wasserstein-Metrik im Spurenzustandsraum“. GAFA, Geom. Funktion. Anal. 11, 1125–1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[35] Eric A. Carlen und Jan Maas. „Ein Analogon der 2-Wasserstein-Metrik in der nichtkommutativen Wahrscheinlichkeit, unter der die fermionische Fokker-Planck-Gleichung ein Gradientenfluss für die Entropie ist“. Komm. Mathematik. Physik. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[36] Eric A. Carlen und Jan Maas. „Gradientenfluss- und Entropieungleichungen für Quanten-Markov-Halbgruppen mit detaillierter Bilanz“. J. Funktion Anal. 273, 1810–1869 (2017).
https: // doi.org/ 10.1016 / j.jfa.2017.05.003

[37] Eric A. Carlen und Jan Maas. „Nichtkommutative Analysis, optimaler Transport und funktionale Ungleichungen in dissipativen Quantensystemen“. J. Stat. Physik. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

[38] Nilanjana Datta und Cambyse Rouzé. „Konzentration von Quantenzuständen aus Quantenfunktions- und Transportkostenungleichungen“. J. Mathe. Physik. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[39] Nilanjana Datta und Cambyse Rouzé. „Zusammenhang von relativer Entropie, optimalem Transport und Fisher-Informationen: Eine Quanten-HWI-Ungleichung“. Ann. Henri Poincaré 21, 2115–2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[40] François Golse, Clément Mouhot und Thierry Paul. „Über das mittlere Feld und die klassischen Grenzen der Quantenmechanik“. Komm. Mathematik. Physik. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[41] François Golse und Thierry Paul. „Die Schrödinger-Gleichung im Mittelfeld- und semiklassischen Regime“. Bogen. Ration. Mech. Anal. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[42] François Golse und Thierry Paul. „Wellenpakete und der quadratische Monge-Kantorovich-Abstand in der Quantenmechanik“. Comptes Rendus Math. 356, 177–197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

[43] François Golse. „Das Quanten-$N$-Körperproblem im Mittelfeld- und semiklassischen Regime“. Phil. Trans. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse und T. Paul. „Quantenoptimaler Transport ist günstiger.“ J. Stat. Physik. 181, 149–162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[45] Emanuele Caglioti, François Golse und Thierry Paul. „Auf dem Weg zum optimalen Transport für Quantendichten“. arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma und Dario Trevisan. „Quantenoptimaler Transport mit Quantenkanälen“. Ann. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan und Seth Lloyd. „Der Quanten-Wasserstein-Abstand der Ordnung 1“. IEEE Trans. Inf. Theorie 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole und Karol Życzkowski. „Quantum Monge-Kantorovich-Problem und Transportentfernung zwischen Dichtematrizen“. Physik. Rev. Lett. 129, 110402 (2022).
https://doi.org/ 10.1103/PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland und Karol Życzkowski. „Quantenoptimaler Transport“. arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein und K. Życzkowski. „Monotonie einer Quanten-2-Wasserstein-Distanz“. J. Phys. A: Mathe. Theor. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos und Dániel Virosztek. „Quanten-Wasserstein-Isometrien im Qubit-Zustandsraum“. J. Mathe. Anal. Appl. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe und Seth Lloyd. „Wasserstein-Komplexität von Quantenschaltungen“. arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu und Seth Lloyd. „Quantendaten mit der Entfernung des Quanten-Erdbewegers lernen“. Quantenwissenschaft. Technol. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[54] EP Wigner und Mutsuo M. Yanase. „Informationsinhalte von Distributionen“. Proz. Natl. Acad. Wissenschaft. USA 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Pawel Horodecki, Michał Horodecki und Karol Horodecki. "Quantenverschränkung". Rev. Mod. Phys. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[56] Otfried Gühne und Géza Tóth. „Verschränkungserkennung“. Physik. Rep. 474, 1–75 (2009).
https://doi.org/ 10.1016/j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik und Marcus Huber. „Verschränkungszertifizierung von der Theorie zum Experiment“. Nat. Rev. Phys. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd und Lorenzo Maccone. „Quantenverstärkte Messungen: Die Standard-Quantengrenze überwinden“. Wissenschaft 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

[59] Matteo GA Paris. „Quantenschätzung für die Quantentechnologie“. Int. J. Quant. Inf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna und Jan Kolodynski. „Kapitel vier – Quantengrenzen in der optischen Interferometrie“. Prog. Optics 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze und Augusto Smerzi. „Quantentheorie der Phasenschätzung“. In GM Tino und MA Kasevich, Herausgeber, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Kurs 188, Varenna). Seiten 691–741. IOS Press, Amsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Géza Tóth und Dénes Petz. „Extreme Eigenschaften der Varianz und der Quanten-Fisher-Information“. Physik. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[63] Sixia Yu. „Quantenfischerinformation als konvexes Dach der Varianz“. arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

[64] Géza Tóth und Florian Fröwis. „Unsicherheitsbeziehungen mit der Varianz und der Quanten-Fisher-Information basierend auf konvexen Zerlegungen von Dichtematrizen“. Physik. Rev. Research 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[65] Shao-Hen Chiew und Manuel Gessner. „Verbesserung der Summenunsicherheitsbeziehungen mit der Quanten-Fisher-Information“. Physik. Rev. Research 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[66] CW Helstrom. „Quantendetektions- und Schätzungstheorie“. Academic Press, New York. (1976). URL: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[67] AS Holevo. „Probabilistische und statistische Aspekte der Quantentheorie“. Nordholland, Amsterdam. (1982).

[68] Samuel L. Braunstein und Carlton M. Caves. „Statistische Distanz und die Geometrie von Quantenzuständen“. Phys. Rev. Lett. 72, 3439–3443 (1994).
https://doi.org/ 10.1103/PhysRevLett.72.3439

[69] Samuel L. Braunstein, Carlton M. Caves und Gerard J. Milburn. „Verallgemeinerte Unsicherheitsrelationen: Theorie, Beispiele und Lorentz-Invarianz“. Ann. Physik. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[70] Dénes Petz. „Quanteninformationstheorie und Quantenstatistik“. Springer, Berlin, Heilerberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[71] Géza Tóth und Iagoba Apellaniz. „Quantenmetrologie aus Sicht der Quanteninformatik“. J. Phys. A: Mathe. Theor. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied und Philipp Treutlein. „Quantenmetrologie mit nichtklassischen Zuständen atomarer Ensembles“. Rev. Mod. Phys. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[73] Marco Barbieri. „Optische Quantenmetrologie“. PRX Quantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

[74] Zoltán Léka und Dénes Petz. „Einige Zerlegungen von Matrixvarianzen“. Wahrscheinlich. Mathematik. Statist. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Dénes Petz und Dániel Virosztek. „Ein Charakterisierungssatz für Matrixvarianzen“. Acta Sci. Mathematik. (Szeged) 80, 681–687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

[76] Akio Fujiwara und Hiroshi Imai. „Ein Faserbündel über Mannigfaltigkeiten von Quantenkanälen und seine Anwendung auf die Quantenstatistik“. J. Phys. A: Mathe. Theor. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[77] BM Escher, RL de Matos Filho und L. Davidovich. „Allgemeiner Rahmen zur Abschätzung der ultimativen Präzisionsgrenze in der verrauschten quantenverstärkten Metrologie“. Nat. Physik. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński und Mădălin Guţă. „Die schwer fassbare Heisenberg-Grenze in der quantenverstärkten Metrologie“. Nat. Komm. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[79] Iman Marvian. „Operative Interpretation von Quantenfischerinformationen in der Quantenthermodynamik“. Physik. Rev. Lett. 129, 190502 (2022).
https://doi.org/ 10.1103/PhysRevLett.129.190502

[80] Reinhard F. Werner. „Quantenzustände mit Einstein-Podolsky-Rosen-Korrelationen, die ein Modell mit versteckten Variablen zulassen“. Physik. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss und M. Lewenstein. „Quantenkorrelationen in Systemen nicht unterscheidbarer Teilchen“. Ann. Physik. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui und Nobuhiro Yonezawa. „Austauschsymmetrie und mehrteilige Verschränkung“. Physik. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[83] Pawel Horodecki. „Trennbarkeitskriterium und untrennbare Mischzustände mit positiver Teiltransposition“. Physik. Lette. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[84] Ascher Peres. „Trennbarkeitskriterium für Dichtematrizen“. Phys. Rev. Lett. 77, 1413–1415 (1996).
https://doi.org/ 10.1103/PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki und Ryszard Horodecki. „Gebundene Verschränkung kann aktiviert werden“. Physik. Rev. Lett. 82, 1056–1059 (1999).
https://doi.org/ 10.1103/PhysRevLett.82.1056

[86] Géza Tóth und Tamás Vértesi. „Quantenzustände mit positiver Teiltransponierung sind für die Metrologie nützlich.“ Physik. Rev. Lett. 120, 020506 (2018).
https://doi.org/ 10.1103/PhysRevLett.120.020506

[87] Scott Hill und William K. Wootters. „Verschränkung eines Paares von Quantenbits“. Physik. Rev. Lett. 78, 5022–5025 (1997).
https://doi.org/ 10.1103/PhysRevLett.78.5022

[88] William K. Wootters. „Verschränkung der Bildung eines beliebigen Zustands zweier Qubits“. Physik. Rev. Lett. 80, 2245–2248 (1998).
https://doi.org/ 10.1103/PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal und Armin Uhlmann. „Verflechtung der Hilfeleistung“. quant-ph/​9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: quant-ph / 9803033

[90] John A. Smolin, Frank Verstraete und Andreas Winter. „Verflechtung von Hilfeleistung und mehrteiliger Staatsdestillation“. Physik. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[91] Holger F. Hofmann und Shigeki Takeuchi. „Verletzung lokaler Unsicherheitsrelationen als Zeichen der Verschränkung“. Physik. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[92] Otfried Gühne. „Charakterisierung der Verschränkung durch Unsicherheitsrelationen“. Physik. Rev. Lett. 92, 117903 (2004).
https://doi.org/ 10.1103/PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth und Peter Adam. „Verschränkungskriterien, die auf lokalen Unsicherheitsbeziehungen basieren, sind grundsätzlich stärker als das berechenbare Kreuznormkriterium.“ Physik. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza und Géza Tóth. „Spin-Squeezing-Ungleichungen für beliebigen Spin“. Physik. Rev. Lett. 107, 240502 (2011).
https://doi.org/ 10.1103/PhysRevLett.107.240502

[95] AR Edmonds. „Drehimpuls in der Quantenmechanik“. Princeton University Press. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[96] Géza Tóth. „Verschränkungserkennung in optischen Gittern bosonischer Atome mit kollektiven Messungen“. Physik. Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne und Hans J. Briegel. „Optimale Spin-Squeezing-Ungleichungen erkennen gebundene Verschränkung in Spinmodellen.“ Physik. Rev. Lett. 99, 250405 (2007).
https://doi.org/ 10.1103/PhysRevLett.99.250405

[98] Géza Tóth und Morgan W. Mitchell. „Erzeugung makroskopischer Singulettzustände in Atomensembles“. Neue J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[99] Géza Tóth. „Nachweis mehrteiliger Verschränkung in der Nähe symmetrischer Dicke-Zustände“. J. Opt. Soc. Bin. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

[100] Géza Tóth, Tobias Moroder und Otfried Gühne. „Bewertung konvexer Dachverschränkungsmaßnahmen“. Physik. Rev. Lett. 114, 160501 (2015).
https://doi.org/ 10.1103/PhysRevLett.114.160501

[101] Lieven Vandenberghe und Stephen Boyd. „Semidefinite Programmierung“. SIAM Review 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[102] Géza Tóth. „Mehrteilige Verschränkung und hochpräzise Metrologie“. Physik. Rev. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé und Augusto Smerzi. „Fisher-Informationen und Mehrteilchenverschränkung“. Physik. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki und Ryszard Horodecki. „Verborgenen messtechnischen Nutzen aktivieren“. Physik. Rev. Lett. 125, 020402 (2020).
https://doi.org/ 10.1103/PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo und Federico M. Spedalieri. „Unterscheidung trennbarer und verschränkter Zustände“. Physik. Rev. Lett. 88, 187904 (2002).
https://doi.org/ 10.1103/PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo und Federico M. Spedalieri. „Vollständige Familie von Trennbarkeitskriterien“. Physik. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo und Federico M. Spedalieri. „Mehrteilige Verschränkung erkennen“. Physik. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[108] Harold Ollivier und Wojciech H. Zurek. „Quantendiskord: Ein Maß für die Quantität von Korrelationen“. Physik. Rev. Lett. 88, 017901 (2001).
https://doi.org/ 10.1103/PhysRevLett.88.017901

[109] L. Henderson und V. Vedral. „Klassische, Quanten- und Gesamtkorrelationen“. J. Phys. A: Mathe. Gen. 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) und Ujjwal Sen. „Quantendiskord und seine Verbündeten: ein Rückblick auf die jüngsten Fortschritte“. Rep. Prog. Physik. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

[111] Dénes Petz. „Kovarianz und Fisher-Information in der Quantenmechanik“. J. Phys. A: Mathe. Gen. 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[112] Paolo Gibilisco, Fumio Hiai und Dénes Petz. „Quantenkovarianz, Quanten-Fisher-Informationen und die Unsicherheitsrelationen“. IEEE Trans. Inf. Theorie 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[113] D. Petz und C. Ghinea. „Einführung in die Quanten-Fisher-Information“. Band 27, Seiten 261–281. Weltwissenschaftlich. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[114] Frank Hansen. „Metrisch angepasste Skew-Informationen“. Proz. Natl. Acad. Wissenschaft. USA 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami und Frank Hansen. „Ein einheitlicher Ansatz zur lokalen Quantenunsicherheit und interferometrischen Leistung durch metrisch angepasste Skew-Informationen“. Entropie 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[116] MATLAB. „9.9.0.1524771(r2020b)“. The MathWorks Inc. Natick, Massachusetts (2020).

[117] MOSEK ApS. „Die MOSEK-Optimierungs-Toolbox für das MATLAB-Handbuch. Version 9.0“. (2019). URL: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[118] J. Löfberg. „YALMIP: Eine Toolbox für Modellierung und Optimierung in MATLAB“. Im Tagungsband der CACSD-Konferenz. Taipeh, Taiwan (2004).

[119] Géza Tóth. „QUBIT4MATLAB V3.0: Ein Programmpaket für Quanteninformationswissenschaft und Quantenoptik für MATLAB“. Berechnen. Physik. Komm. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[120] Das Paket QUBIT4MATLAB ist unter https://​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433 und auf der persönlichen Homepage https://​/​gtoth.eu/​qubit4matlab.html verfügbar.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Zitiert von

[1] Laurent Lafleche, „Quantenoptimaler Transport und schwache Topologien“, arXiv: 2306.12944, (2023).

Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2023, 10:16:14 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.

Konnte nicht abrufen Crossref zitiert von Daten während des letzten Versuchs 2023-10-16 14:47:42: Von Crossref konnten keine zitierten Daten für 10.22331 / q-2023-10-16-1143 abgerufen werden. Dies ist normal, wenn der DOI kürzlich registriert wurde.

Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.

Zeitstempel:

Mehr von Quantenjournal