Eine auf künstlicher Intelligenz basierende Lösung für Sudoku

Eine auf künstlicher Intelligenz basierende Lösung für Sudoku

Zeitstempel: 29. Januar 2024, 9:40 Uhr
Quellknoten: 3091242

Der 29. Januar ist Nationaler Puzzle-Tag und zur Feier haben wir einen unterhaltsamen Blog erstellt, der detailliert beschreibt, wie man Sudoku mithilfe künstlicher Intelligenz (KI) löst.

Einleitung

Vorher Wordle, der Sudoku-Rätsel war der letzte Schrei und erfreut sich immer noch großer Beliebtheit. In den letzten Jahren ist die Verwendung von Optimierung Methoden zur Lösung des Rätsels waren ein vorherrschendes Thema. Sehen „Sudoku-Rätsel mithilfe der Optimierung in Arkieva lösen".

Heutzutage konzentriert sich der Einsatz von KI auf maschinelles Lernen, das eine breite Palette von Methoden von der Lasso-Regression bis zum verstärkenden Lernen umfasst. Der Einsatz von KI hat wieder aufgetaucht Komplexes anzugehen Planung Herausforderungen. Eine Methode, die Suche mit Backtracking, wird häufig verwendet und eignet sich perfekt für Sudoku.

In diesem Blog finden Sie eine detaillierte Beschreibung, wie Sie Sudoku mit dieser Methode lösen können. Wie sich herausstellt, findet sich „Backtracking“ in Optimierungs- und Machine-Learning-Engines und ist ein Eckpfeiler der fortschrittlichen Heuristiken, die Arkieva für die Planung verwendet. Der Algorithmus ist in einer „Array Programming Language“ implementiert, einer funktionsorientierten Programmiersprache, die a verarbeitet reichhaltiger Satz an Array-Strukturen.

Grundlagen von Sudoku

Aus Wikipedia: Sudoku ist ein logikbasiertes, kombinatorisches Zahlenrätsel. Das Ziel besteht darin, ein 9×9-Gitter mit Ziffern zu füllen, sodass jede Spalte, jede Zeile und jedes der neun 3×3-Untergitter, aus denen das Gitter besteht (auch „Boxen“, „Blöcke“, „Regionen“ genannt), oder „Unterquadrate“) enthält alle Ziffern von 1 bis 9. Der Puzzle-Setter stellt ein teilweise vollständiges Raster bereit, das normalerweise eine eindeutige Lösung hat. Abgeschlossene Rätsel sind immer eine Art lateinisches Quadrat mit einer zusätzlichen Einschränkung für den Inhalt einzelner Regionen. Beispielsweise darf dieselbe einzelne Ganzzahl nicht zweimal in derselben Zeile oder Spalte des 9×9-Spielbretts oder in einem der neun 3×3-Unterbereiche des 9×9-Spielbretts vorkommen.

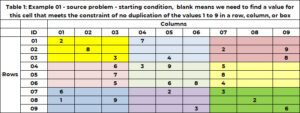
Tabelle 1 enthält ein Beispielproblem. Es gibt 9 Zeilen und 9 Spalten für insgesamt 81 Zellen. Jede darf nur eine von neun ganzen Zahlen zwischen 1 und 9 haben. In der Ausgangslösung hat eine Zelle entweder einen einzelnen Wert – wodurch der Wert in dieser Zelle auf diesen Wert festgelegt wird, oder die Zelle ist leer, was darauf hinweist, dass wir sie benötigen um einen Wert für diese Zelle zu finden. Die Zelle (1,1) hat den Wert 2 und Zelle (6,5) hat den Wert 6. Zelle (1,2) und Zelle (2,3) sind leer und der Algorithmus findet einen Wert für diese Zellen.

Die Komplikation

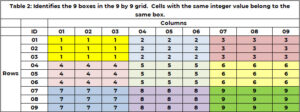
Eine Zelle gehört nicht nur zu einer einzigen Zeile und Spalte, sondern auch zu nur einer Box. Es gibt 1 Kästchen, die in Tabelle 9 farblich gekennzeichnet sind. Tabelle 1 verwendet eine eindeutige Ganzzahl zwischen 2 und 1, um jedes Kästchen oder Raster zu identifizieren. Die Zellen mit einem Zeilenwert von (9, 1 oder 2) und einem Spaltenwert von (3, 1 oder 2) gehören zu Feld 3. Feld 1 enthält Zeilenwerte von (6, 4, 5) und Spaltenwerte (6, 7). , 8). Die Box-ID wird durch die Formel BOX_ID = {9x(floor((ROW_ID-3) /1)} + Decke (COL_ID/3) bestimmt. Für die Zelle (3) ist 5,7 = 6x(floor(3-5 ))/1) + Decke (3/8)= 3×3 + 1 = 3+3.

Das Herzstück des Puzzles

Um einen ganzzahligen Wert zwischen 1 und 9 für jede unbekannte Zelle zu finden, sodass die ganzen Zahlen 1 bis 9 einmal und nur einmal für jede Spalte, jede Zeile und jedes Kästchen verwendet werden.

Schauen wir uns die leere Zelle (1,3) an. Zeile 1 enthält bereits die Werte 2 und 7. Diese sind in dieser Zelle nicht zulässig. Spalte 3 enthält bereits die Werte 3, 5,6, 7,9. Diese sind nicht erlaubt. Feld 1 (gelb) hat die Werte 2, 3 und 8. Diese sind nicht zulässig. Die folgenden Werte sind nicht zulässig (2,7); (3, 5, 6, 7, 9); (2, 3, 8). Die nicht zulässigen eindeutigen Werte sind (2, 3, 5, 6, 7, 8, 9). Die einzigen Kandidatenwerte sind (1,4).

Ein Lösungsansatz wäre, der Zelle (1) vorübergehend 1,3 zuzuweisen und dann zu versuchen, Kandidatenwerte für eine andere Zelle zu finden.

Eine Backtracking-Lösung: Startkomponenten

Array-Struktur

Der Ausgangspunkt besteht darin, sich für eine Array-Struktur zu entscheiden, um das Quellproblem zu speichern und die Suche zu unterstützen. Tabelle 3 hat diese Array-Struktur. Spalte 1 ist eine eindeutige Ganzzahl-ID für jede Zelle. Die Werte reichen von 1 bis 81. Spalte 2 ist die Zeilen-ID der Zelle. Spalte 3 ist die Spalten-ID der Zelle. Spalte 4 ist die Box-ID. Spalte 5 ist der Wert in der Zelle. Beobachten Sie, dass eine Zelle ohne Wert den Wert Null anstelle von Leerzeichen oder Null erhält. Dadurch bleibt es ein „Nur-Ganzzahl-Array“ – was die Leistung weit übertrifft.

In APL würde dieses Array in einem zweidimensionalen Array gespeichert, dessen Form 2 x 81 beträgt. Angenommen, die Elemente von Tabelle 5 werden in der Variablen MAT gespeichert. Beispielfunktionen sind:

Der Befehl MAT[1 2 3;] erfasst die ersten drei Zeilen von MAT
1 1 1 1 2
2 1 2 1 0
3 1 3 1 0
MAT[1 2 3; 4 5] sichert die Zeilen 1, 2, 3 und nur die Spalten 4 und 5
1
1
1
(MAT[;5]=0)/MAT[;1] findet alle Zellen, die einen Wert benötigen.

TABELLE 3 EINFÜGEN

Plausibilitätsprüfung: Duplikate

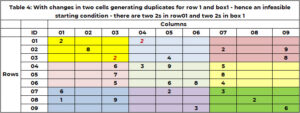
Vor Beginn der Suche ist unbedingt eine Plausibilitätsprüfung durchzuführen! Das ist die mögliche Ausgangslösung. Für Sudoku ist es möglich, dass es jetzt Duplikate in jeder Zeile, Spalte oder Box gibt. Die aktuelle Ausgangslösung, zum Beispiel 1, ist machbar. Tabelle 4 enthält ein Beispiel, bei dem die Ausgangslösung Duplikate aufweist. Zeile 1 hat zwei Werte 2. Bereich 1 hat zwei Werte 2. Die Funktion „SANITY_DUPE“ verarbeitet diese Logik.

Plausibilitätsprüfung: Optionen für Zellen ohne Werte

Eine sehr hilfreiche Information wären alle möglichen Werte für eine Zelle ohne Wert. Wenn es keine Kandidaten gibt, ist dieses Rätsel nicht lösbar. Eine Zelle kann keinen Wert annehmen, der bereits von ihrem Nachbarn beansprucht wird. Unter Verwendung von Tabelle 1 für Zelle (1,3,'1' – diese letzte 1 ist die Boxid), sind ihre Nachbarn Zeile 1, Spalte 3 und Box 1. Zeile 1 hat die Werte (2,7); Spalte 3 hat die Werte (3,5,6,7,9); Box 1 hat die Werte (2,3,8). Zelle (1,3.1) kann die folgenden Werte nicht annehmen (2,3,5,6,7,8,9). Die einzigen Optionen für Zelle (1,3,1) sind (1,4). Für Zelle (4,1,2) werden die Werte 1, 2, 3, 5, 6, 7, 9 bereits in Zeile 4, Spalte 1 und/oder Feld 4 verwendet. Die einzigen Kandidatenwerte sind (4,8) . Die Funktion „SANITY_CAND“ übernimmt diese Logik.

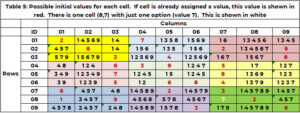
Tabelle 5 zeigt die Kandidaten, zum Beispiel 1, zu Beginn des Suchprozesses. Wurde einer Zelle in den Startbedingungen (Tabelle 1) bereits ein Wert zugewiesen, wird dieser Wert wiederholt und rot dargestellt. Wenn eine Zelle, die einen Wert benötigt, nur eine Option hat, wird diese weiß angezeigt. Zelle (8,7,9) hat den Einzelwert 7 in Weiß. (2,5,8,4,3) werden von Nachbarspalte 7 beansprucht. (1, 2, 9) von Zeile 8. (3,2,6) von Feld 9. Nur der Wert 7 wird nicht beansprucht.

Sanity Check: Auf der Suche nach Konflikten

Die Informationen, die alle Optionen für Zellen identifizieren, die einen Wert benötigen (veröffentlicht in Tabelle 4), ermöglichen es uns, einen Konflikt zu identifizieren, bevor wir mit dem Suchvorgang beginnen. Ein Konflikt tritt auf, wenn zwei Zellen, die einen Wert benötigen, nur einen Kandidaten haben, der Kandidatenwert derselbe ist und die beiden Zellen Nachbarn sind. Aus Tabelle 4 wissen wir, dass die einzige Zelle, die einen Wert benötigt und nur einen Kandidaten hat, Zelle (8,7,9) ist. Beispiel 1: Es liegt kein Konflikt vor.

Was wäre ein Konflikt? Wenn der einzig mögliche Wert für Zelle (3,7,3) 7 (anstelle von 1, 6, 7) war, liegt ein Konflikt vor. Zelle (8,7) und Zelle (3,7) sind Nachbarn – dieselbe Spalte. Wenn jedoch der einzig mögliche Wert für Zelle (4,9,2) 7 (anstelle von 1, 2, 7) wäre, wäre dies kein Konflikt. Diese Zellen sind keine Nachbarn.

Zusammenfassung der Sanitätsprüfung

  1. Bei Duplikaten ist die Ausgangslösung nicht realisierbar.
  2. Wenn eine Zelle, die einen Wert benötigt, keine Kandidaten hat, dann gibt es keine mögliche Lösung für dieses Rätsel. Die Liste der Kandidatenwerte für jede Zelle kann verwendet werden, um den Suchraum zu reduzieren – sowohl für Backtracking als auch für die Optimierung.
  3. Die Fähigkeit, Konflikte zu finden, zeigt, dass das Rätsel ohne einen Suchprozess nicht realisierbar ist – es gibt keine Lösung. Darüber hinaus werden die „Problemzellen“ identifiziert.

Eine Backtracking-Lösung: Suchprozess

Sobald die Kerndatenstrukturen und die Plausibilitätsprüfung vorhanden sind, richten wir unsere Aufmerksamkeit auf den Suchprozess. Das wiederkehrende Thema ist wieder die Einrichtung von Datenstrukturen zur Unterstützung der Suche.

Verfolgung der Suche

Das Array Tracker behält den Überblick über die erledigten Aufgaben

  1. Spalte 1 ist der Zähler
  2. Spalte 2 ist die Anzahl der verfügbaren Optionen, die dieser Zelle zugewiesen werden können
    • 1 bedeutet 1 verfügbare Option, 2 bedeutet zwei Optionen usw.
    • 0 bedeutet – keine Option verfügbar oder Zurücksetzen auf 0 (kein zugewiesener Wert) und Zurückverfolgen
  3. Spalte 3 ist die Zelle, der eine Wertindexnummer (1 bis 81) zugewiesen wurde.
  4. Spalte 4 ist der der Zelle im Trackverlauf zugewiesene Wert
    • Ein Wert von 9999 bedeutet, dass die Sackgasse in dieser Zelle gefunden wurde
    • Der Wert einer Ganzzahl zwischen 1 und 9 (einschließlich) ist der Wert, der dieser Zelle an diesem Punkt des Suchvorgangs zugewiesen wird.
    • Ein Wert von 0 bedeutet, dass diese Zelle eine Zuweisung benötigt

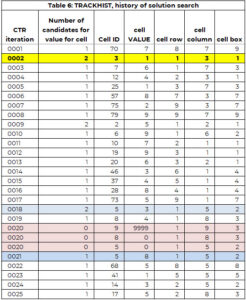
Das Tracker-Array dient zur Unterstützung des Suchvorgangs. Das Array TRACKHIST hat die gleiche Struktur wie der Tracker, speichert jedoch den Verlauf des gesamten Suchvorgangs. Tabelle 6 enthält einen Teil von TRACKHIST für Beispiel 1. Dies wird in einem späteren Abschnitt ausführlicher erläutert.

Zusätzlich das Array PAV (ein Vektor eines Vektors) verfolgt die zuvor dieser Zelle zugewiesenen Werte. Dadurch wird sichergestellt, dass wir eine fehlgeschlagene Lösung nicht erneut prüfen – ähnlich wie bei TABU.

Es gibt einen optionalen Protokollprozess, bei dem der Suchprozess jeden Schritt ausschreibt.

Starten der Suche

Nachdem die Buchhaltung und die Plausibilitätsprüfung abgeschlossen sind, können wir nun mit der Suche beginnen. Die Schritte sind:

  1. Gibt es noch Zellen, die einen Wert benötigen? – wenn nein, dann sind wir fertig.
  2. Suchen Sie für jede Zelle, die einen Wert benötigt, alle Kandidatenoptionen für jede Zelle. Tabelle 4 enthält diese Werte zu Beginn des Lösungsprozesses. Bei jeder Iteration wird dies aktualisiert, um den den Zellen zugewiesenen Werten Rechnung zu tragen.
  3. Bewerten Sie die Optionen in dieser Reihenfolge.
    • Wenn eine Zelle NULL Optionen hat, leiten Sie ein Backtracking ein
    • Finden Sie alle Zellen mit einer Option, wählen Sie eine dieser Zellen aus, nehmen Sie diese Zuordnung vor,
      1. und aktualisieren Sie die Tracking-Tabelle, die aktuelle Lösung und PAV.
    • Wenn alle Zellen mehr als eine Option haben, wählen Sie eine Zelle und einen Wert aus und aktualisieren Sie
      1. und aktualisieren Sie die Tracking-Tabelle, die aktuelle Lösung und PAV

Wir verwenden Tabelle 6, die Teil des Verlaufs des Lösungsprozesses ist (TRACKHIST genannt), um jeden Schritt zu veranschaulichen.

In der ersten Iteration (CTR=1) wird Zelle 70 (Zeile 8, Spalte 7, Feld 9) ausgewählt, um ihr einen Wert zuzuweisen. Es gibt nur den Kandidaten (7), und dieser Wert wird der Zelle 70 zugewiesen. Zusätzlich wird der Wert 7 zum Vektor der zuvor zugewiesenen Werte (PAV) für Zelle 70 hinzugefügt.

In der zweiten Iteration wird der Zelle 30 der Wert 1 zugewiesen. Diese Zelle hatte zwei Kandidatenwerte. Der Zelle wird der kleinste Kandidatenwert zugewiesen (nur eine willkürliche Regel, um die Logik leicht verständlich zu machen).

Der Prozess der Identifizierung einer Zelle, die einen Wert benötigt, und der Zuweisung eines Werts funktioniert bis zur Iteration (CTR) 20 einwandfrei. Zelle 9 benötigt einen Wert, aber die Anzahl der Kandidaten ist NULL. Es gibt zwei Möglichkeiten:

  • Für dieses Rätsel gibt es keine Lösung.
  • Wir machen einige Zuweisungen rückgängig (zurückverfolgen) und gehen einen anderen Weg.

Wir haben nach der Zellenzuordnung gesucht, die dieser am nächsten kommt und bei der es mehr als eine Option gab. In diesem Beispiel geschah dies bei Iteration 18, wo Zelle 5 der Wert 3 zugewiesen wurde, es jedoch zwei Kandidatenwerte für Zelle 5 gab – die Werte 3 und 8.

Zwischen Zelle 5 (CTR = 18) und Zelle 9 (CTR = 20) wird Zelle 8 der Wert 4 (CTR = 19) zugewiesen. Wir setzen die Zellen 8 und 5 wieder auf die Liste „Benötige einen Wert“. Dies wird im zweiten und dritten CTR=20-Eintrag erfasst, wobei der Wert auf 0 gesetzt wird. Der Wert 3 wird im PAV-Vektor für Zelle 5 beibehalten. Das heißt, die Suchmaschine kann der Zelle 3 den Wert 5 nicht zuweisen.

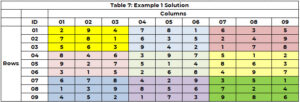
Die Suchmaschine startet erneut, um einen Wert für Zelle 5 zu identifizieren (wobei 3 keine Option mehr ist) und weist Zelle 8 den Wert 5 zu (CTR=21). Dies wird fortgesetzt, bis alle Zellen einen Wert haben oder es eine Zelle ohne Option gibt und kein Backtracking-Pfad mehr vorhanden ist. Die Lösung ist in Tabelle 7 aufgeführt.

Beachten Sie, dass dort, wo es mehr als einen Kandidaten für eine Zelle gibt, eine Chance für eine parallele Verarbeitung besteht.

Vergleich mit der MILP-Optimierungslösung

Oberflächlich betrachtet ist die Darstellung des Sudoku-Rätsels völlig anders. Der KI-Ansatz verwendet ganze Zahlen und bietet in jeder Hinsicht eine genauere und intuitivere Darstellung. Darüber hinaus liefern die Sanity Checker hilfreiche Informationen, um eine stärkere Formulierung zu erstellen. Die MILP-Darstellung ist endlos Binärdateien (0/1). Angesichts der Stärke moderner MILP-Löser sind die Binärdateien jedoch leistungsstarke Darstellungen.

Intern behält der MILP-Solver jedoch nicht die Binärdateien bei, sondern verwendet eine Sparse-Array-Methode, um die Speicherung aller Nullen zu vermeiden. Darüber hinaus entstehen die Algorithmen zur Lösung von Binärdateien erst in den 1980er und 1990er Jahren. Der Aufsatz von 1983 Crowder, Johnson und Padberg berichtet über eine der ersten praktischen Lösungen der Optimierung mit Binärdateien. Sie weisen darauf hin, wie wichtig eine clevere Vorverarbeitung und Branch-and-Bound-Methoden für eine erfolgreiche Lösung sind.

Die jüngste Explosion des Einsatzes von Constraint-Programmierung und Software wie z lokaler Löser hat deutlich gemacht, wie wichtig es ist, KI-Methoden mit den ursprünglichen Optimierungsmethoden wie linearer Programmierung und kleinsten Quadraten zu verwenden.

Zeitstempel:

Mehr von Arkiewa