Gaussisk naiv Bayes, forklaret

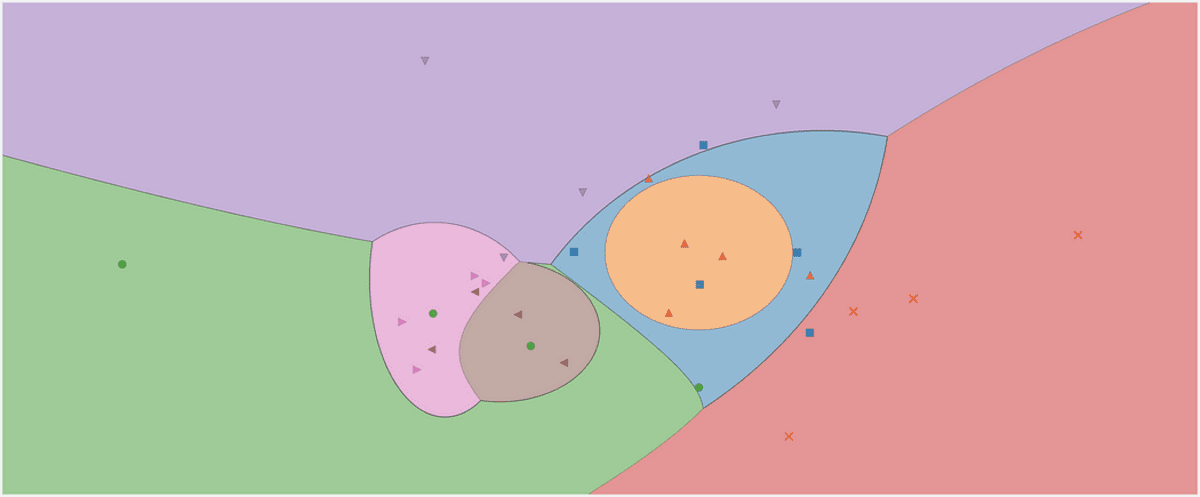
Beslutningsregionen for en gaussisk naiv Bayes-klassifikator. Billede af forfatteren.

Jeg tror, ​​at dette er en klassiker i begyndelsen af ​​hver datavidenskabskarriere: den Naiv Bayes Classifier. Eller jeg burde hellere sige det familie af naive Bayes-klassifikatorer, da de findes i mange varianter. For eksempel er der en multinomial naiv Bayes, en Bernoulli-naiv Bayes og også en Gaussisk naiv Bayes-klassifikator, der hver især er forskellig i kun en lille detalje, som vi vil finde ud af. De naive Bayes-algoritmer er ret enkle i designet, men viste sig at være nyttige i mange komplekse situationer i den virkelige verden.

I denne artikel kan du lære

• hvordan de naive Bayes klassifikatorer fungerer,
• hvorfor det giver mening at definere dem som de er og
• hvordan man implementerer dem i Python ved hjælp af NumPy.

Du kan finde koden på min Github.

Det kan måske hjælpe lidt at tjekke min primer om Bayesiansk statistik En blid introduktion til Bayesiansk inferens at vænne sig til Bayes-formlen. Da vi vil implementere klassificeringen på en scikit-læringskonform måde, er det også umagen værd at tjekke min artikel Byg din egen tilpassede scikit-learn-regression. Scikit-learn overhead er dog ret lille, og du burde kunne følge med alligevel.

Vi vil begynde at udforske den forbavsende enkle teori om naiv Bayes-klassificering og derefter vende os til implementeringen.

Hvad er vi egentlig interesserede i, når vi klassificerer? Hvad laver vi egentlig, hvad er input og output? Svaret er enkelt:

Givet et datapunkt x, hvad er sandsynligheden for, at x hører til en klasse c?

Det er alt, hvad vi vil svare med enhver klassifikation. Du kan direkte modellere dette udsagn som en betinget sandsynlighed: p(c|x).

For eksempel, hvis der er

• 3 klasser c1, c₂, c3og
• x består af 2 funktioner x₁, x₂,

resultatet af en klassificering kunne være noget lignende p(c1|x₁, x₂) = 0.3, p(c₂|x₁, x₂)=0.5 og p(c3|x₁, x₂)=0.2. Hvis vi holder af en enkelt etiket som output, ville vi vælge den med størst sandsynlighed, dvs c₂ med en sandsynlighed på 50 % her.

Den naive Bayes-klassifikator forsøger at beregne disse sandsynligheder direkte.

Naiv Bayes

Ok, så givet et datapunkt x, vi ønsker at beregne p(c|x) for alle klasser c og udsend derefter c med størst sandsynlighed. I formler ser man ofte dette som

Billede af forfatteren.

Bemærk: max p(c|x) returnerer den maksimale sandsynlighed, mens argmax p(c|x) returnerer c med denne højeste sandsynlighed.

Men før vi kan optimere p(c|x), skal vi være i stand til at beregne det. Til dette bruger vi Bayes' sætning:

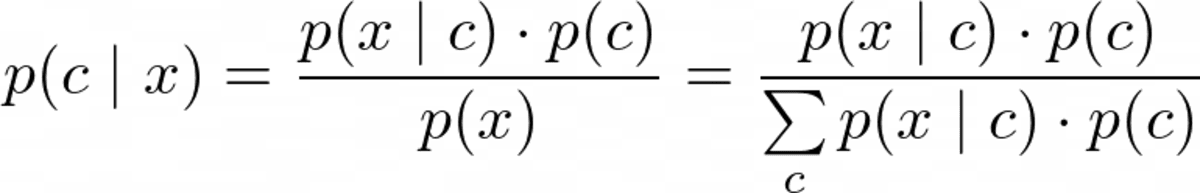
Bayes sætning. Billede af forfatteren.

Dette er Bayes-delen af ​​naive Bayes. Men nu har vi følgende problem: Hvad er p(x|c) og p(c)?

Det er, hvad træningen af ​​en naiv Bayes-klassifikator handler om.

Træningen

For at illustrere alt, lad os bruge et legetøjsdatasæt med to rigtige funktioner x₁, x₂og tre klasser c1, c₂, c3 i det følgende.

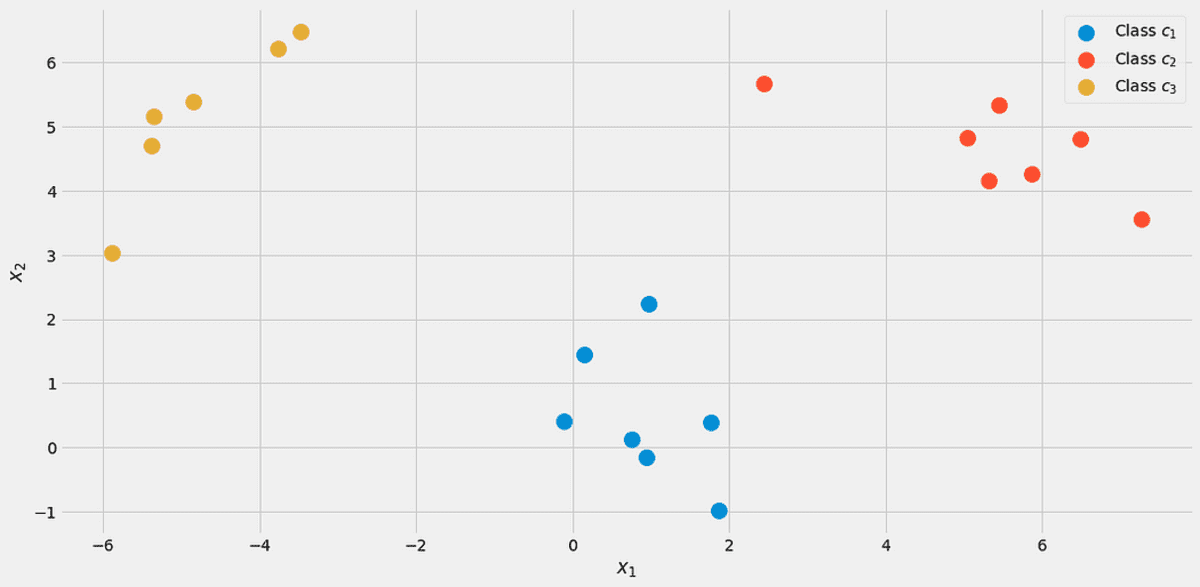
Dataene, visualiseret. Billede af forfatteren.

Du kan oprette dette nøjagtige datasæt via

from sklearn.datasets import make_blobs X, y = make_blobs(n_samples=20, centers=[(0,0), (5,5), (-5, 5)], random_state=0)

Lad os starte med klasses sandsynlighed p(c), sandsynligheden for, at nogle klasse c er observeret i det mærkede datasæt. Den enkleste måde at estimere dette på er blot at beregne de relative frekvenser af klasserne og bruge dem som sandsynligheder. Vi kan bruge vores datasæt til at se, hvad det præcis betyder.

Der er 7 ud af 20 point mærket klasse c1 (blå) i datasættet, derfor siger vi p(c1)=7/20. Vi har 7 point til klassen c₂ (rød) også, derfor sætter vi p(c₂)=7/20. Den sidste klasse c3 (gul) har derfor kun 6 point p(c3)=6/20.

Denne simple beregning af klassens sandsynligheder ligner en maksimal sandsynlighedstilgang. Du kan dog også bruge en anden forudgående distribution, hvis du vil. For eksempel, hvis du ved, at dette datasæt ikke er repræsentativt for den sande population, fordi klasse c3 skulle dukke op i 50 % af tilfældene, så indstiller du p(c1) = 0.25, p(c₂)=0.25 og p(c3)=0.5. Uanset hvad der hjælper dig med at forbedre ydeevnen på testsættet.

Vi henvender os nu til sandsynlighed p(x|c)=p(x₁, x₂|c). En tilgang til at beregne denne sandsynlighed er at filtrere datasættet for prøver med etiket c og prøv derefter at finde en fordeling (f.eks. en 2-dimensionel Gaussian), der fanger funktionerne x₁, x₂.

Desværre har vi normalt ikke nok prøver pr. klasse til at foretage en korrekt vurdering af sandsynligheden.

For at kunne bygge en mere robust model laver vi naiv antagelse at funktionerne x₁, x₂ er stokastisk uafhængig, givet c. Dette er bare en fancy måde at gøre matematikken nemmere via

Billede af forfatteren

for hver klasse c. Det er her, naiv del af naive Bayes kommer fra, fordi denne ligning ikke holder generelt. Alligevel giver den naive Bayes gode, nogle gange fremragende resultater i praksis. Især for NLP-problemer med bag-of-word-funktioner skinner den multinomiale naive Bayes.

Argumenterne ovenfor er de samme for enhver naiv Bayes-klassifikator, du kan finde. Nu kommer det bare an på hvordan du modellerer p(xXNUMX|cXNUMX), p(xXNUMX|cXNUMX), p(xXNUMX|cXNUMX), p(xXNUMX|cXNUMX), p(xXNUMX|cXNUMX) , p(x₂|c₃).

Hvis dine funktioner kun er 0 og 1, kan du bruge en Bernoulli distribution. Hvis de er heltal, a Multinomial fordeling. Vi har dog reelle funktionsværdier og beslutter os for en Gauss distribution, deraf navnet Gaussisk naive Bayes. Vi antager følgende form

Billede af forfatteren.

hvor μᵢ,ⱼ er middelværdien og σᵢ,ⱼ er den standardafvigelse, som vi skal estimere ud fra dataene. Det betyder, at vi får et gennemsnit for hver funktion i sammen med en klasse cⱼ, i vores tilfælde betyder 2*3=6. Det samme gælder standardafvigelserne. Dette kalder på et eksempel.

Lad os prøve at vurdere μ₂,₁ , σ₂,₁. Fordi j=1, vi er kun interesserede i klassen c1, lad os kun beholde prøver med denne etiket. Følgende prøver er tilbage:

# samples with label = c_1 array([[ 0.14404357, 1.45427351], [ 0.97873798, 2.2408932 ], [ 1.86755799, -0.97727788], [ 1.76405235, 0.40015721], [ 0.76103773, 0.12167502], [-0.10321885, 0.4105985 ], [ 0.95008842, -0.15135721]])

Nu på grund af i=2 vi skal kun overveje den anden kolonne. μ₂,₁ er middelværdien og σ₂,₁ standardafvigelsen for denne kolonne, dvs μ₂, 0.49985176 = XNUMX og σ₂, 0.9789976 = XNUMX.

Disse tal giver mening, hvis du ser på scatter-plot fra oven igen. Funktionerne x₂ af prøverne fra klassen c1 er omkring 0.5, som du kan se på billedet.

Vi beregner dette nu for de andre fem kombinationer, og vi er færdige!

I Python kan du gøre det sådan:

from sklearn.datasets import make_blobs
import numpy as np # Create the data. The classes are c_1=0, c_2=1 and c_3=2.
X, y = make_blobs( n_samples=20, centers=[(0, 0), (5, 5), (-5, 5)], random_state=0
) # The class probabilities.
# np.bincounts counts the occurence of each label.
prior = np.bincount(y) / len(y) # np.where(y==i) returns all indices where the y==i.
# This is the filtering step.
means = np.array([X[np.where(y == i)].mean(axis=0) for i in range(3)])
stds = np.array([X[np.where(y == i)].std(axis=0) for i in range(3)])

Vi modtager

# priors
array([0.35, 0.35, 0.3 ])
# means array([[ 0.90889988, 0.49985176], [ 5.4111385 , 4.6491892 ], [-4.7841679 , 5.15385848]])
# stds
array([[0.6853714 , 0.9789976 ], [1.40218915, 0.67078568], [0.88192625, 1.12879666]])

Dette er resultatet af træningen af ​​en gaussisk naiv Bayes-klassifikator.

At forudsige

Den komplette forudsigelsesformel er

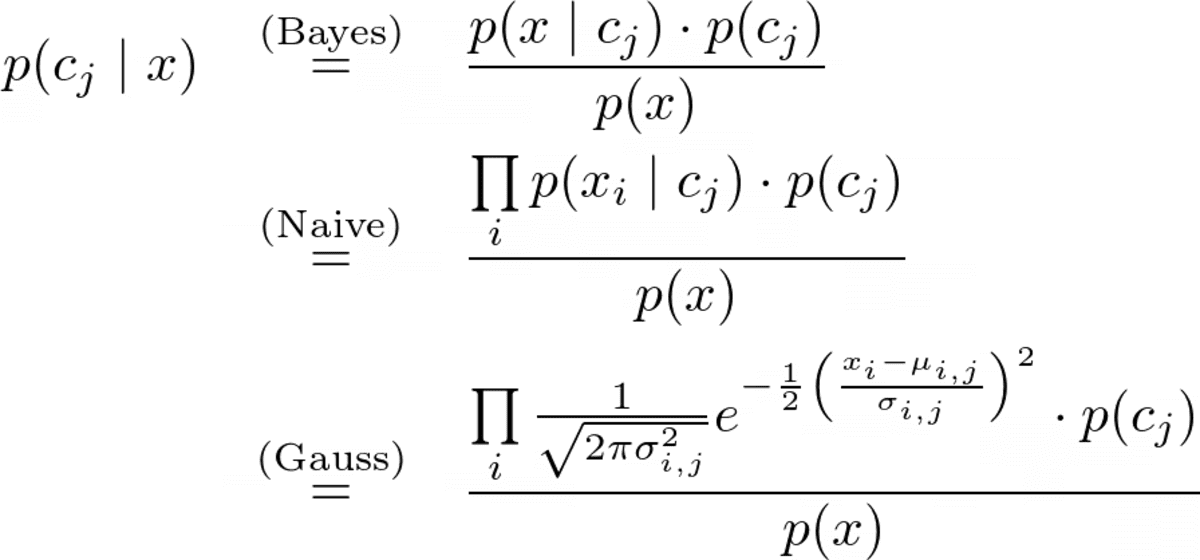
Billede af forfatteren.

Lad os antage et nyt datapunkt x*=(-2, 5) kommer ind.

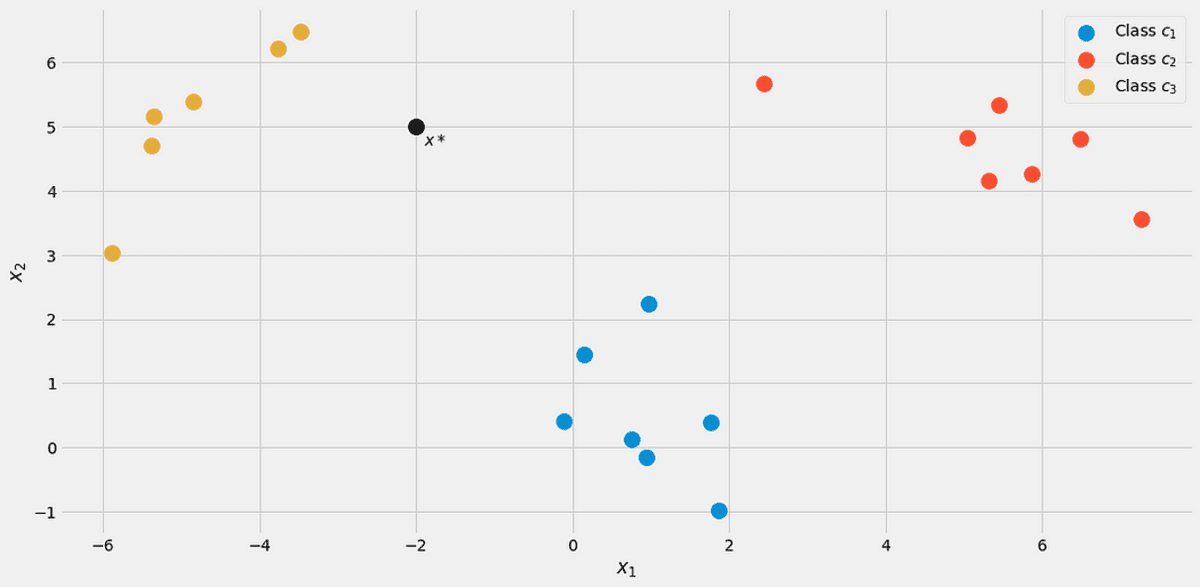
Billede af forfatteren.

Lad os beregne, hvilken klasse den tilhører p(c|x*) for alle klasser. Fra billedet skulle det tilhøre klassen c3 = 2, men lad os se. Lad os ignorere nævneren p(x) et sekund. Ved hjælp af følgende sløjfe beregnes nominatorerne for j = 1, 2, 3.

x_new = np.array([-2, 5]) for j in range(3): print( f"Probability for class {j}: {(1/np.sqrt(2*np.pi*stds[j]**2)*np.exp(-0.5*((x_new-means[j])/stds[j])**2)).prod()*p[j]:.12f}" )

Vi modtager

Probability for class 0: 0.000000000263
Probability for class 1: 0.000000044359
Probability for class 2: 0.000325643718

Selvfølgelig disse sandsynligheder (vi bør ikke kalde dem sådan) ikke lægge op til én, da vi ignorerede nævneren. Dette er dog ikke noget problem, da vi bare kan tage disse unormaliserede sandsynligheder og dividere dem med deres sum, så vil de summere til én. Så ved at dividere disse tre værdier med deres sum på omkring 0.00032569, får vi

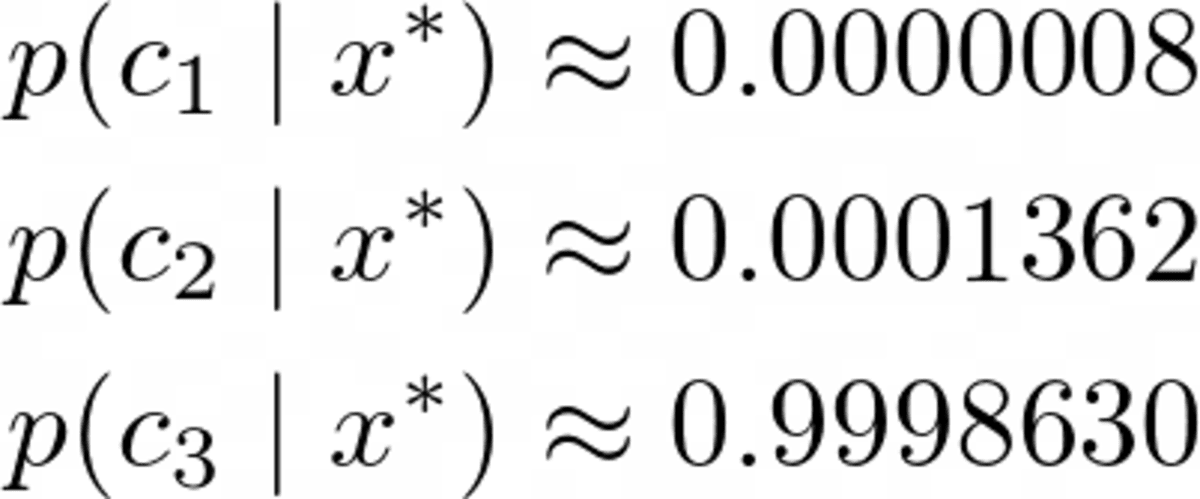
Billede af forfatteren.

En klar vinder, som vi forventede. Lad os nu implementere det!

Denne implementering er langtfra effektiv, ikke numerisk stabil, den tjener kun et uddannelsesformål. Vi har diskuteret det meste, så det burde være nemt at følge med nu. Du kan ignorere alle check funktioner, eller læs min artikel Byg din egen skræddersyede scikit-learn hvis du er interesseret i, hvad de præcist gør.

Bemærk blot, at jeg implementerede en predict_proba metode først til at beregne sandsynligheder. Metoden predict kalder bare denne metode og returnerer indekset (=klasse) med den højeste sandsynlighed ved hjælp af en argmax-funktion (der er det igen!). Klassen afventer klasser fra 0 til k-1, hvor k er antallet af klasser.

import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted class GaussianNaiveBayesClassifier(BaseEstimator, ClassifierMixin): def fit(self, X, y): X, y = check_X_y(X, y) self.priors_ = np.bincount(y) / len(y) self.n_classes_ = np.max(y) + 1 self.means_ = np.array( [X[np.where(y == i)].mean(axis=0) for i in range(self.n_classes_)] ) self.stds_ = np.array( [X[np.where(y == i)].std(axis=0) for i in range(self.n_classes_)] ) return self def predict_proba(self, X): check_is_fitted(self) X = check_array(X) res = [] for i in range(len(X)): probas = [] for j in range(self.n_classes_): probas.append( ( 1 / np.sqrt(2 * np.pi * self.stds_[j] ** 2) * np.exp(-0.5 * ((X[i] - self.means_[j]) / self.stds_[j]) ** 2) ).prod() * self.priors_[j] ) probas = np.array(probas) res.append(probas / probas.sum()) return np.array(res) def predict(self, X): check_is_fitted(self) X = check_array(X) res = self.predict_proba(X) return res.argmax(axis=1)

Test af implementering

Selvom koden er ret kort, er den stadig for lang til at være helt sikker på, at vi ikke har lavet nogen fejl. Så lad os tjekke, hvordan det klarer sig i forhold til scikit-learn GaussianNB-klassifikator.

my_gauss = GaussianNaiveBayesClassifier()
my_gauss.fit(X, y)
my_gauss.predict_proba([[-2, 5], [0,0], [6, -0.3]])

udgange

array([[8.06313823e-07, 1.36201957e-04, 9.99862992e-01], [1.00000000e+00, 4.23258691e-14, 1.92051255e-11], [4.30879705e-01, 5.69120295e-01, 9.66618838e-27]])

Forudsigelserne ved hjælp af predict metode er

# my_gauss.predict([[-2, 5], [0,0], [6, -0.3]])
array([2, 0, 1])

Lad os nu bruge scikit-learn. Smid noget kode ind

from sklearn.naive_bayes import GaussianNB gnb = GaussianNB()
gnb.fit(X, y)
gnb.predict_proba([[-2, 5], [0,0], [6, -0.3]])

udbytter

array([[8.06314158e-07, 1.36201959e-04, 9.99862992e-01], [1.00000000e+00, 4.23259111e-14, 1.92051343e-11], [4.30879698e-01, 5.69120302e-01, 9.66619630e-27]])

Tallene ligner nogenlunde dem i vores klassificering, men de er en lille smule forskudt i de sidste par viste cifre. Gjorde vi noget forkert? Nej. Scikit-learn-versionen bruger blot et andet hyperparameter var_smoothing=1e-09 . Hvis vi indstiller denne til nul, får vi præcis vores tal. Perfekt!

Tag et kig på beslutningsregionerne i vores klassifikator. Jeg markerede også de tre punkter, vi brugte til test. Det ene punkt tæt på grænsen har kun 56.9 % chance for at tilhøre den røde klasse, som du kan se fra predict_proba udgange. De to andre punkter er klassificeret med meget højere selvtillid.

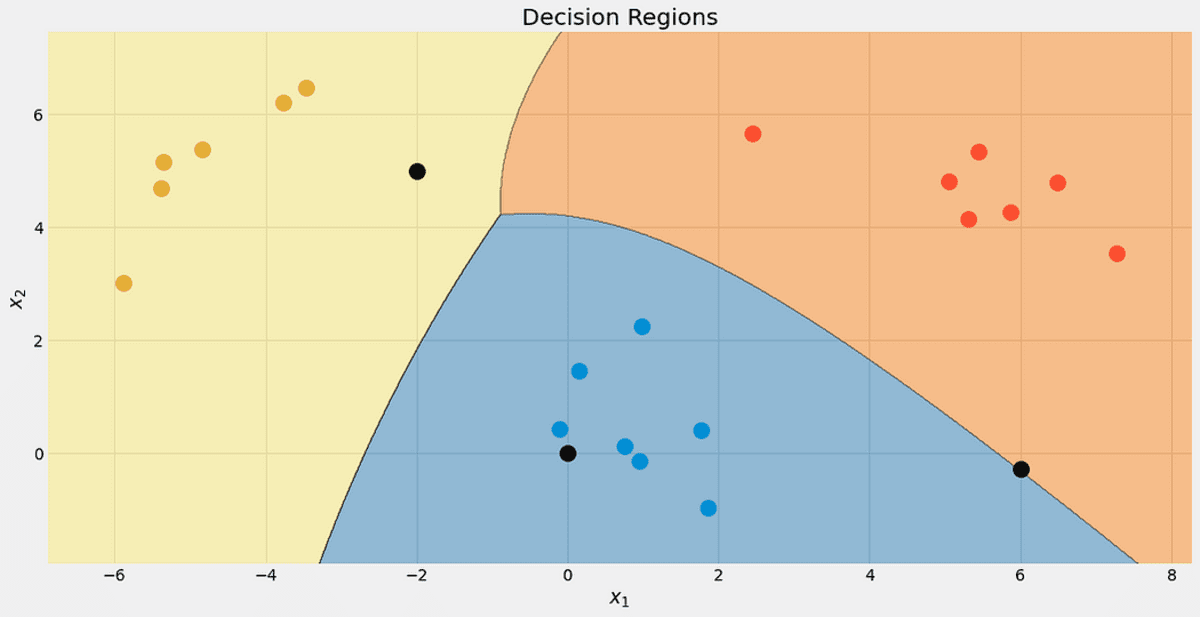
Beslutningsregionerne med de 3 nye punkter. Billede af forfatteren.

I denne artikel har vi lært, hvordan den gaussiske naive Bayes-klassifikator virker og gav en intuition om, hvorfor den blev designet på den måde - det er en direkte tilgang til at modellere sandsynligheden for interesse. Sammenlign dette med logistisk regression: der modelleres sandsynligheden ved hjælp af en lineær funktion med en sigmoid-funktion påført ovenpå. Det er stadig en nem model, men den føles ikke så naturlig som en naiv Bayes-klassificering.

Vi fortsatte med at regne nogle få eksempler og samle nogle nyttige stykker kode undervejs. Endelig har vi implementeret en komplet Gaussisk naiv Bayes-klassifikator på en måde, der fungerer godt med scikit-learn. Det betyder, at du for eksempel kan bruge det i pipelines eller grid-søgning.

Til sidst foretog vi et lille fornuftstjek ved at importere scikit-learns egen Gauss-naive Bayes-klassifikator og teste om begge, vores og scikit-learns klassifikator giver det samme resultat. Denne test var vellykket.

 
 
Dr. Robert Kübler er dataforsker hos Publicis Media og forfatter hos Towards Data Science.

 
Original. Genopslået med tilladelse.
 

• SEO Powered Content & PR Distribution. Bliv forstærket i dag.
• Platoblokkæde. Web3 Metaverse Intelligence. Viden forstærket. Adgang her.
• Kilde: https://www.kdnuggets.com/2023/03/gaussian-naive-bayes-explained.html?utm_source=rss&utm_medium=rss&utm_campaign=gaussian-naive-bayes-explained