[مرآة] البرامج الحسابية التربيعية: من الصفر إلى البطل

فيتاليك بوتيرين عبر مدونة فيتاليك بوتيرين

هذه مرآة لهذا المنصب في https://medium.com/@VitalikButerin/برامج-حسابية-تربيعية-من-صفر-إلى-بطل-f6d558cea649

كان هناك الكثير من الاهتمام في الآونة الأخيرة بالتكنولوجيا الكامنة وراء zk-SNARKs، وقد أصبح الناس مهتمين بشكل متزايد محاولة إزالة الغموض وهو شيء أصبح الكثيرون يطلقون عليه "رياضيات القمر" نظرًا لتعقيدها الهائل الذي لا يمكن فك شفرته. إن فهم zk-SNARKs يمثل تحديًا كبيرًا بالفعل، خاصة بسبب العدد الهائل من الأجزاء المتحركة التي تحتاج إلى التجمع معًا حتى يعمل الأمر برمته، ولكن إذا قمنا بتقسيم التكنولوجيا قطعة قطعة، يصبح فهمها أسهل.

الغرض من هذا المنشور ليس بمثابة مقدمة كاملة لـ zk-SNARKs؛ يفترض كمعرفة أساسية أنك (1) تعرف ما هي zk-SNARKs وماذا تفعل، و(2) تعرف ما يكفي من الرياضيات لتتمكن من التفكير في أشياء مثل كثيرات الحدود (إذا كانت العبارة �( �)+�( �) =( �+ �)(�) ، حيث � و � كثيرة الحدود، تبدو طبيعية وواضحة بالنسبة لك، فأنت في المستوى الصحيح). بدلاً من ذلك، يتعمق المقال بشكل أعمق في الآلية التي تقف وراء هذه التكنولوجيا، ويحاول أن يشرح قدر الإمكان النصف الأول من خط الأنابيب، كما رسمه الباحث في zk-SNARK إيران ترومر هنا:

يمكن تقسيم الخطوات هنا إلى نصفين. أولاً، لا يمكن تطبيق zk-SNARKs على أي مشكلة حسابية مباشرة؛ بل يجب عليك تحويل المشكلة إلى "النموذج" الصحيح حتى تعمل المشكلة. يُطلق على النموذج اسم "البرنامج الحسابي التربيعي" (QAP)، وتحويل كود دالة إلى واحدة منها هو في حد ذاته أمر غير تافه إلى حد كبير. إلى جانب عملية تحويل كود دالة إلى QAP، هناك عملية أخرى يمكن تشغيلها جنبًا إلى جنب بحيث إذا كان لديك مدخلاً للكود، يمكنك إنشاء حل مناسب (يسمى أحيانًا "شاهد" على QAP). بعد ذلك، هناك عملية أخرى معقدة إلى حد ما لإنشاء "دليل المعرفة الصفري" الفعلي لهذا الشاهد، وعملية منفصلة للتحقق من الدليل الذي يمرره شخص آخر إليك، ولكن هذه تفاصيل خارج نطاق هذا المنشور .

المثال الذي سنختاره هو مثال بسيط: إثبات أنك تعرف حل المعادلة التكعيبية: �3+�+5=35 (تلميح: الإجابة هي 3). هذه المشكلة بسيطة بما فيه الكفاية بحيث لن تكون عملية QAP الناتجة كبيرة جدًا بحيث تكون مخيفة، ولكنها ليست تافهة بما يكفي بحيث يمكنك رؤية جميع الآليات تلعب دورها.

دعونا نكتب وظيفتنا على النحو التالي:

def qeval(x):
    y = x**3
    return x + y + 5

لغة البرمجة البسيطة ذات الأغراض الخاصة التي نستخدمها هنا تدعم العمليات الحسابية الأساسية (+، −، ⋅، /)، الأس الثابت ( � 7 ولكن ليس �� ) والتخصيص المتغير، وهو قوي بما يكفي بحيث يمكنك القيام به نظريًا أي حساب بداخله (طالما أن عدد الخطوات الحسابية محدد، ولا يسمح بالحلقات). لاحظ أن معاملات المعامل (%) وعوامل المقارنة (<، >، ≥، ≥) غير مدعومة، حيث لا توجد طريقة فعالة لإجراء المعامل أو المقارنة مباشرة في حساب المجموعة الدورية المحدودة (كن شاكرًا لهذا؛ إذا كانت هناك طريقة للقيام بأي منهما، سيتم كسر تشفير المنحنى الناقص بشكل أسرع مما يمكنك قوله "بحث ثنائي" و"نظرية الباقي الصينية").

يمكنك توسيع اللغة لتشمل modulo والمقارنات من خلال توفير تحليلات البت (على سبيل المثال 13=23+22+1) كمدخلات مساعدة، وإثبات صحة تلك التحليلات وإجراء العمليات الحسابية في الدوائر الثنائية؛ في حساب المجالات المحدودة، يعد إجراء عمليات التحقق من المساواة (==) أمرًا ممكنًا أيضًا وفي الواقع أسهل قليلاً، لكن هاتين التفاصيل لن نتطرق إليها الآن. يمكننا توسيع اللغة لدعم الشروط الشرطية (على سبيل المثال if �<5: �=7؛ else: �=9) عن طريق تحويلها إلى صيغة حسابية: �=7⋅( �<5)+9⋅( �≥5 ) مع ملاحظة أنه يجب تنفيذ كلا "المسارين" للشرط الشرطي، وإذا كان لديك العديد من الشروط الشرطية المتداخلة، فقد يؤدي ذلك إلى قدر كبير من النفقات العامة.

دعونا الآن نتناول هذه العملية خطوة بخطوة. إذا كنت تريد القيام بذلك بنفسك لأي جزء من التعليمات البرمجية، فأنا نفذت مترجم هنا (للأغراض التعليمية فقط؛ لست مستعدًا لإنشاء QAPs لـ zk-SNARKs في العالم الحقيقي حتى الآن!).

تسطيح

الخطوة الأولى هي إجراء "التسطيح"، حيث نقوم بتحويل الكود الأصلي، الذي قد يحتوي على عبارات وتعبيرات معقدة بشكل اعتباطي، إلى سلسلة من العبارات التي تكون في شكلين: �= � (حيث يمكن أن يكون � متغيرًا أو رقمًا ) و ��= � (��) � (حيث �� يمكن أن تكون + و − و ⋅ و / و � و � يمكن أن تكون متغيرات أو أرقام أو تعبيرات فرعية بحد ذاتها). يمكنك اعتبار كل من هذه العبارات بمثابة البوابات المنطقية في الدائرة. نتيجة عملية التسطيح للكود أعلاه هي كما يلي:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

إذا قرأت الكود الأصلي والكود هنا، فيمكنك بسهولة أن ترى أن الاثنين متساويان.

بوابات R1CS

الآن، نقوم بتحويل هذا إلى شيء يسمى نظام القيد من المرتبة الأولى (R1CS). R1CS عبارة عن سلسلة من مجموعات من ثلاثة متجهات ( �، �، �)، وحل R1CS هو متجه �، حيث � يجب أن يحقق المعادلة �. �⋅ �. �− �. � = 1، حيث . يمثل حاصل الضرب النقطي - بعبارات أبسط، إذا قمنا "بالضغط معًا" - و - بضرب القيمتين في نفس الموضع، ثم أخذنا مجموع هذه المنتجات، ثم نفعل الشيء نفسه مع - و - وبعد ذلك - و � ، فإن النتيجة الثالثة تساوي حاصل ضرب النتيجتين الأوليين. على سبيل المثال، هذا هو R0CS راضٍ:

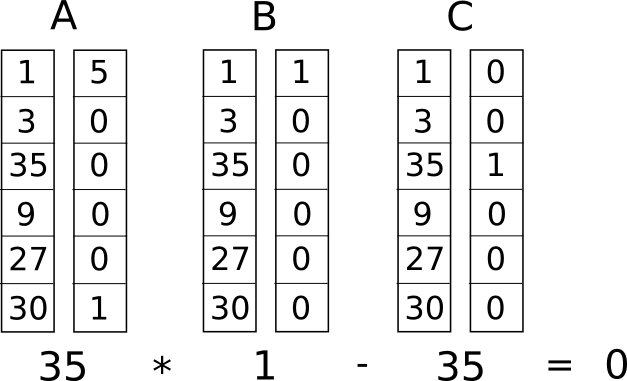
ولكن بدلاً من وجود قيد واحد فقط، سيكون لدينا العديد من القيود: واحد لكل بوابة منطقية. هناك طريقة قياسية لتحويل البوابة المنطقية إلى ثلاثية ( �، � ، �) اعتمادًا على العملية (+ أو − أو ⋅ أو /) وما إذا كانت الوسائط عبارة عن متغيرات أو أرقام. طول كل متجه يساوي إجمالي عدد المتغيرات في النظام، بما في ذلك متغير وهمي ~واحد في الفهرس الأول يمثل الرقم 1، ومتغيرات الإدخال، ومتغير وهمي ~out يمثل الإخراج، ثم كل من المتغيرات الوسيطة (���1 و ���2 أعلاه)؛ ستكون المتجهات عمومًا متفرقة جدًا، حيث تملأ فقط الفجوات المقابلة للمتغيرات التي تتأثر ببعض البوابات المنطقية المحددة.

أولاً، سنوفر تعيين المتغير الذي سنستخدمه:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

سيتألف متجه الحل من تعيينات لكل هذه المتغيرات بهذا الترتيب.

الآن، سنعطي (،،،،) ثلاثية للبوابة الأولى:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

يمكنك أن ترى أنه إذا كان متجه الحل يحتوي على 3 في الموضع الثاني، و9 في الموضع الرابع، فبغض النظر عن بقية محتويات متجه الحل، فإن فحص المنتج النقطي سوف يتلخص في 3⋅3=9، و لذلك سوف يمر. إذا كان متجه الحل يحتوي على −3 في الموضع الثاني و9 في الموضع الرابع، فسيتم اجتياز الاختبار أيضًا؛ في الواقع، إذا كان متجه الحل يحتوي على 7 في الموضع الثاني و49 في الموضع الرابع، فسيظل هذا الفحص ناجحًا - والغرض من هذا الفحص الأول هو التحقق من اتساق مدخلات ومخرجات البوابة الأولى فقط.

والآن ننتقل إلى البوابة الثانية:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

بأسلوب مشابه للتحقق من المنتج النقطي الأول، نحن هنا نتحقق من أن "1⋅" = �.

والآن البوابة الثالثة:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

هنا، النمط مختلف إلى حد ما: فهو ضرب العنصر الأول في متجه الحل بالعنصر الثاني، ثم بالعنصر الخامس، وإضافة النتيجتين، والتحقق مما إذا كان المجموع يساوي العنصر السادس. نظرًا لأن العنصر الأول في متجه الحل يكون دائمًا واحدًا، فهذا مجرد فحص جمع، للتحقق من أن المخرجات تساوي مجموع المدخلين.

وأخيراً البوابة الرابعة:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

هنا، نقوم بتقييم الفحص الأخير، ~out =������2+5. يعمل فحص الضرب النقطي عن طريق أخذ العنصر السادس في متجه الحل، وإضافة خمسة أضعاف العنصر الأول (تذكير: العنصر الأول هو 1، لذلك يعني هذا فعليًا إضافة 5)، والتحقق منه مقابل العنصر الثالث، وهو المكان الذي نقوم فيه تخزين متغير الإخراج.

وهناك لدينا R1CS مع أربعة قيود. الشاهد هو ببساطة تعيين لجميع المتغيرات، بما في ذلك المدخلات والمخرجات والمتغيرات الداخلية:

[1, 3, 35, 9, 27, 30]

يمكنك حساب ذلك بنفسك ببساطة عن طريق "تنفيذ" التعليمات البرمجية المسطحة أعلاه، والبدء بتعيين متغير الإدخال = 3، ووضع قيم جميع المتغيرات الوسيطة والمخرجات أثناء حسابها.

مجموعة R1CS الكاملة هي:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS إلى QAP

الخطوة التالية هي أخذ R1CS وتحويله إلى نموذج QAP، الذي يطبق نفس المنطق تمامًا باستثناء استخدام كثيرات الحدود بدلاً من المنتجات النقطية. نقوم بهذا على النحو التالي. ننتقل 3 من أربع مجموعات من ثلاثة متجهات بطول ستة إلى ست مجموعات من ثلاث كثيرات الحدود من الدرجة 3، حيث نقيم كثيرات الحدود عند كل منها إحداثي س يمثل أحد القيود. بمعنى، إذا قمنا بتقييم كثيرات الحدود عند �=1، فسنحصل على المجموعة الأولى من المتجهات، وإذا قمنا بتقييم كثيرات الحدود عند �=2، فسنحصل على المجموعة الثانية من المتجهات، وهكذا.

يمكننا إجراء هذا التحويل باستخدام شيء يسمى أ استيفاء لاغرانج. المشكلة التي يحلها استيفاء لاغرانج هي: إذا كان لديك مجموعة من النقاط (أي ( �، �) أزواج إحداثية)، فإن إجراء استيفاء لاغرانج على تلك النقاط يمنحك كثيرة الحدود التي تمر عبر كل تلك النقاط. نقوم بذلك عن طريق تحليل المشكلة: لكل إحداثي، نقوم بإنشاء كثير الحدود الذي يحتوي على الإحداثي المطلوب عند ذلك الإحداثي وإحداثي 0 في جميع الإحداثيات الأخرى التي نهتم بها، ثم نحصل على النتيجة النهائية النتيجة نجمع كل كثيرات الحدود معا.

دعونا نفعل مثالا. لنفترض أننا نريد كثيرة الحدود التي تمر عبر (1,3،2,2)، (3,4،1,3) و (2,0،3,0). نبدأ بتكوين كثيرة الحدود التي تمر عبر (1)، (XNUMX،XNUMX) و (XNUMX،XNUMX). كما اتضح، فإن إنشاء كثيرة حدود "تبرز" عند = XNUMX وتكون صفرًا عند النقاط الأخرى محل الاهتمام هو أمر سهل؛ نحن ببساطة نفعل:

(x - 2) * (x - 3)

الذي يشبه هذا:

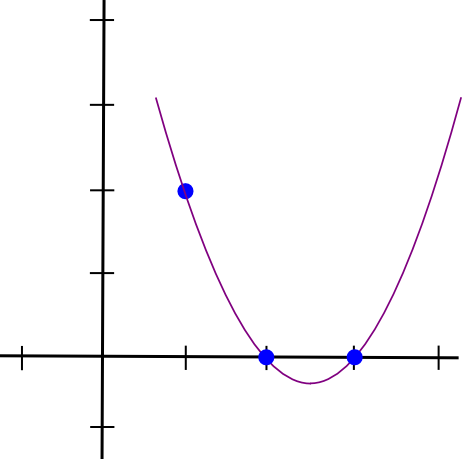
الآن، نحتاج فقط إلى "إعادة قياسه" بحيث يكون الارتفاع عند x=1 صحيحًا:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

هذا يعطينا:

1.5 * x**2 - 7.5 * x + 9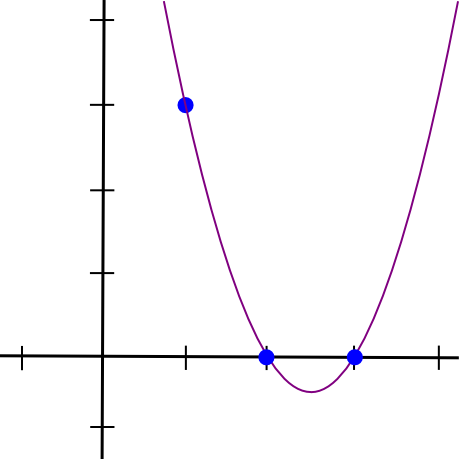

ثم نفعل الشيء نفسه مع النقطتين الأخريين، ونحصل على كثيرتي حدود أخريين متشابهتين، باستثناء أنهما "يبرزان" عند = 2 و = 3 بدلاً من = 1. نجمع الثلاثة معًا ونحصل على:

1.5 * x**2 - 5.5 * x + 7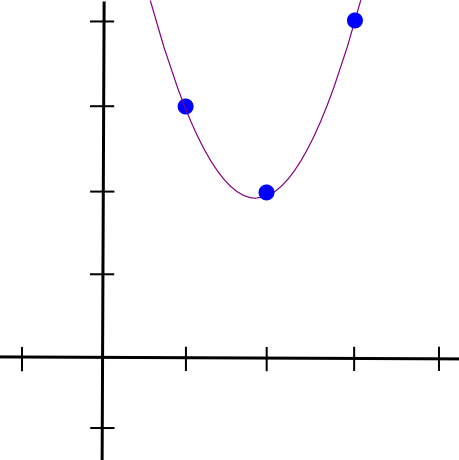

مع الإحداثيات التي نريدها بالضبط. تستغرق الخوارزمية كما هو موضح أعلاه وقتا ( �3)، حيث أن هناك نقاط وكل نقطة تتطلب � ( �2) وقتا لضرب كثيرات الحدود معًا؛ مع القليل من التفكير، يمكن تقليل هذا إلى وقت (-2)، ومع الكثير من التفكير، باستخدام خوارزميات تحويل فورييه السريعة وما شابه، يمكن تقليله إلى أبعد من ذلك - وهو تحسين بالغ الأهمية عند استخدام الوظائف في zk -SNARKs في الممارسة العملية غالبًا ما تحتوي على عدة آلاف من البوابات.

الآن، دعونا نستخدم استيفاء لاغرانج لتحويل R1CS. ما سنفعله هو أخذ القيمة الأولى من كل متجه، واستخدام استيفاء لاغرانج لإنشاء كثيرة الحدود من ذلك (حيث يؤدي تقييم كثير الحدود عند إلى الحصول على القيمة الأولى للمتجه )، وكرر العملية للقيمة الأولى لكل ناقل � و �، ثم كرر هذه العملية للقيم الثانية، والثالثة، والقيم، وما إلى ذلك. وللتيسير سأقدم الإجابات الآن:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

المعاملات مرتبة تصاعديًا، لذا فإن كثيرة الحدود الأولى أعلاه هي في الواقع 0.833⋅�3—5⋅�2+9.166⋅�5. تشكل هذه المجموعة من كثيرات الحدود (بالإضافة إلى كثيرات الحدود Z التي سأشرحها لاحقًا) المعلمات الخاصة بمثيل QAP هذا. لاحظ أن كل العمل حتى هذه النقطة يجب أن يتم تنفيذه مرة واحدة فقط لكل وظيفة تحاول استخدام zk-SNARKs للتحقق منها؛ بمجرد إنشاء معلمات QAP، يمكن إعادة استخدامها.

دعونا نحاول تقييم كل هذه كثيرات الحدود عند = 1. إن تقييم كثيرة الحدود عند �=1 يعني ببساطة جمع جميع المعاملات (مثل 1 �=1 للجميع �)، لذا فالأمر ليس صعبًا. نحن نحصل:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

وها هو ما لدينا هنا يماثل تمامًا مجموعة المتجهات الثلاثة للبوابة المنطقية الأولى التي أنشأناها أعلاه.

التحقق من QAP

والآن ما الفائدة من هذا التحول المجنون؟ الجواب هو أنه بدلاً من التحقق من القيود في R1CS بشكل فردي، يمكننا الآن التحقق كل القيود في نفس الوقت عن طريق إجراء فحص المنتج النقطي على كثيرات الحدود.

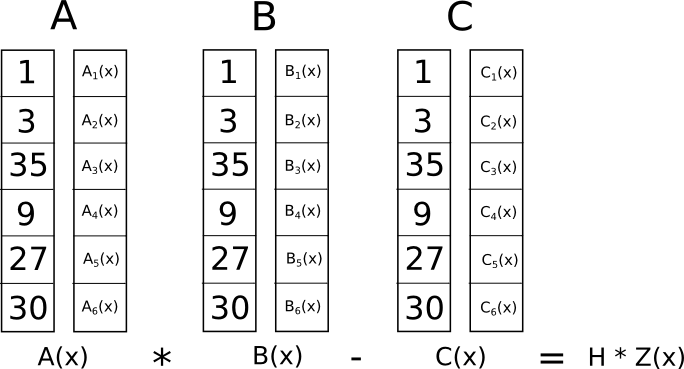
نظرًا لأن اختبار الضرب النقطي في هذه الحالة عبارة عن سلسلة من عمليات الإضافة والضرب لكثيرات الحدود، فإن النتيجة نفسها ستكون كثيرة الحدود. إذا كان كثير الحدود الناتج، الذي تم تقييمه عند كل إحداثي استخدمناه أعلاه لتمثيل بوابة منطقية، يساوي الصفر، فهذا يعني أن جميع الاختبارات قد نجحت؛ إذا تم تقييم متعدد الحدود الناتج على الأقل من الإحداثيات التي تمثل بوابة منطقية يعطي قيمة غير صفرية، فهذا يعني أن القيم الداخلة والخارجة من تلك البوابة المنطقية غير متناسقة (على سبيل المثال، البوابة هي ��= �⋅��) �1 ولكن قد تكون القيم المتوفرة �=2 و �1=2 و �=5).

لاحظ أن كثيرة الحدود الناتجة لا يجب أن تكون في حد ذاتها صفرًا، وفي الواقع لن تكون كذلك في معظم الحالات؛ يمكن أن يكون لها أي سلوك عند النقاط التي لا تتوافق مع أي بوابات منطقية، طالما أن النتيجة صفر في جميع النقاط التي do تتوافق مع بعض البوابة. للتحقق من الصحة، نحن في الواقع لا نقيم كثيرة الحدود ��������������������� عند كل نقطة تقابل البوابة؛ بدلاً من ذلك، نقسم - على كثيرة حدود أخرى، -، ونتأكد من أن - يقسم بالتساوي - أي أن القسمة -/ - لا تترك أي باقي.

� يتم تعريفه كـ ( � −1) ⋅ ( � −2) ⋅ ( � −3) … – أبسط كثير الحدود يساوي الصفر في جميع النقاط التي تتوافق مع البوابات المنطقية. إنها حقيقة أولية للجبر أي وقت كثيرة الحدود التي تساوي صفرًا في كل هذه النقاط يجب أن تكون من مضاعفات كثيرة الحدود الدنيا هذه، وإذا كانت كثيرة الحدود من مضاعفات - فإن تقييمها عند أي من هذه النقاط سيكون صفرًا؛ وهذا التكافؤ يجعل مهمتنا أسهل بكثير.

الآن، دعونا نتحقق من حاصل الضرب النقطي مع كثيرات الحدود أعلاه. أولاً، كثيرات الحدود المتوسطة:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

الآن، ����������������������������������:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

الآن، الحد الأدنى كثير الحدود �=( �−1)⋅(�−2)⋅( �−3)⋅( �−4):

Z = [24, -50, 35, -10, 1]

وإذا قسمنا النتيجة أعلاه على � نحصل على:

h = t / Z = [-3.666, 17.055, -3.444]

مع عدم وجود بقية.

وبالتالي لدينا الحل لمشكلة QAP. إذا حاولنا تزوير أي من المتغيرات في حل R1CS الذي نشتق منه حل QAP - على سبيل المثال، قم بتعيين الأخير على 31 بدلاً من 30، فسنحصل على متعدد الحدود يفشل في إحدى عمليات التحقق (في هذا الخصوص في الحالة، فإن النتيجة عند = 3 ستكون −1 بدلاً من 0)، علاوة على ذلك، لن تكون من مضاعفات �؛ بدلاً من ذلك، فإن قسمة ��/ � سيعطي ما تبقى من [−5.0,8.833,−4.5,0.666].

لاحظ أن ما سبق هو تبسيط؛ "في العالم الحقيقي"، لن تتم عمليات الجمع والضرب والطرح والقسمة مع الأعداد العادية، بل مع عناصر الحقول المحدودة - وهو نوع مخيف من العمليات الحسابية المتسقة ذاتيًا، لذلك لا تزال جميع القوانين الجبرية التي نعرفها ونحبها هذا صحيح، ولكن عندما تكون جميع الإجابات عبارة عن عناصر من مجموعة محدودة الحجم، عادةً ما تكون أعداد صحيحة ضمن النطاق من 0 إلى −1 للبعض . على سبيل المثال، إذا كان � = 13، فإن 1/2 = 7 (و 7⋅2=1)، و3⋅5=2، وهكذا. يؤدي استخدام حساب المجال المحدود إلى إزالة الحاجة إلى القلق بشأن أخطاء التقريب ويسمح للنظام بالعمل بشكل جيد مع المنحنيات الإهليلجية، والتي تصبح في النهاية ضرورية لبقية آلية zk-SNARK التي تجعل بروتوكول zk-SNARK آمنًا بالفعل.

شكر خاص لإيران ترومر لمساعدته في شرح العديد من التفاصيل حول الأعمال الداخلية لـ zk-SNARKs لي.

• محتوى مدعوم من تحسين محركات البحث وتوزيع العلاقات العامة. تضخيم اليوم.
• PlatoData.Network Vertical Generative Ai. تمكين نفسك. الوصول هنا.
• أفلاطونايستريم. ذكاء Web3. تضخيم المعرفة. الوصول هنا.
• أفلاطون كربون، كلينتك ، الطاقة، بيئة، شمسي، إدارة المخلفات. الوصول هنا.
• أفلاطون هيلث. التكنولوجيا الحيوية وذكاء التجارب السريرية. الوصول هنا.
• BlockOffsets. تحديث ملكية الأوفست البيئية. الوصول هنا.
• المصدر ذكاء بيانات أفلاطون.