通过量子上下文冗余的随机访问代码

通过量子上下文冗余的随机访问代码

时间戳记：13年2023月6日，凌晨16:XNUMX
源节点： 1898879

吉安卡洛·加蒂1,2,3, 丹尼尔·胡尔加1, 恩里克·索拉诺1,4,5,6及 米克尔·桑兹1,2,5,7

1巴斯克大学UPV / EHU物理化学系，西班牙毕尔巴鄂Apartado644 48080
2巴斯克大学 EHU 量子中心 UPV/EHU
3量子 MADS, Uribitarte Kalea 6, 48001 毕尔巴鄂, 西班牙
4上海大学国际量子人工智能科技中心（QuArtist）和物理系，上海 200444
5IKERBASQUE，巴斯克科学基金会，Plaza Euskadi 5, 48009 毕尔巴鄂，西班牙
6Kipu Quantum, Greifswalderstrasse 226, 10405 柏林, 德国
7巴斯克应用数学中心 (BCAM), Alameda de Mazarredo 14, 48009 Bilbao, 巴斯克地区, 西班牙

觉得本文有趣或想讨论？ 在SciRate上发表评论或发表评论.

抽象

我们提出了一种协议，利用量子相关性作为随机访问码，对多体泡利可观测量的测量统计中的经典位进行编码。使用这些可观察量构建的测量上下文会产生具有内在冗余的结果，我们通过将数据编码为一组方便的上下文本征态来利用这一点。这允许用很少的资源随机访问编码数据。使用的本征态是高度纠缠的，可以通过低深度的离散参数化量子电路生成。该协议的应用包括需要仅部分检索的大数据存储的算法，就像决策树的情况一样。使用 $n$-qubit 状态，该量子随机访问码比 $nge 14$ 的经典对应代码以及 $nge 16$ 的先前量子随机访问码具有更大的成功概率。此外，对于$nge 18$，它可以放大为几乎无损的压缩协议，成功概率为$0.999$，压缩率为$O(n^2/2^n)$。它可以存储的数据相当于 Google-Drive 服务器容量（$n= 44$），相当于国际象棋的强力解决方案（在任何棋盘配置上做什么）（$n= 100$）。

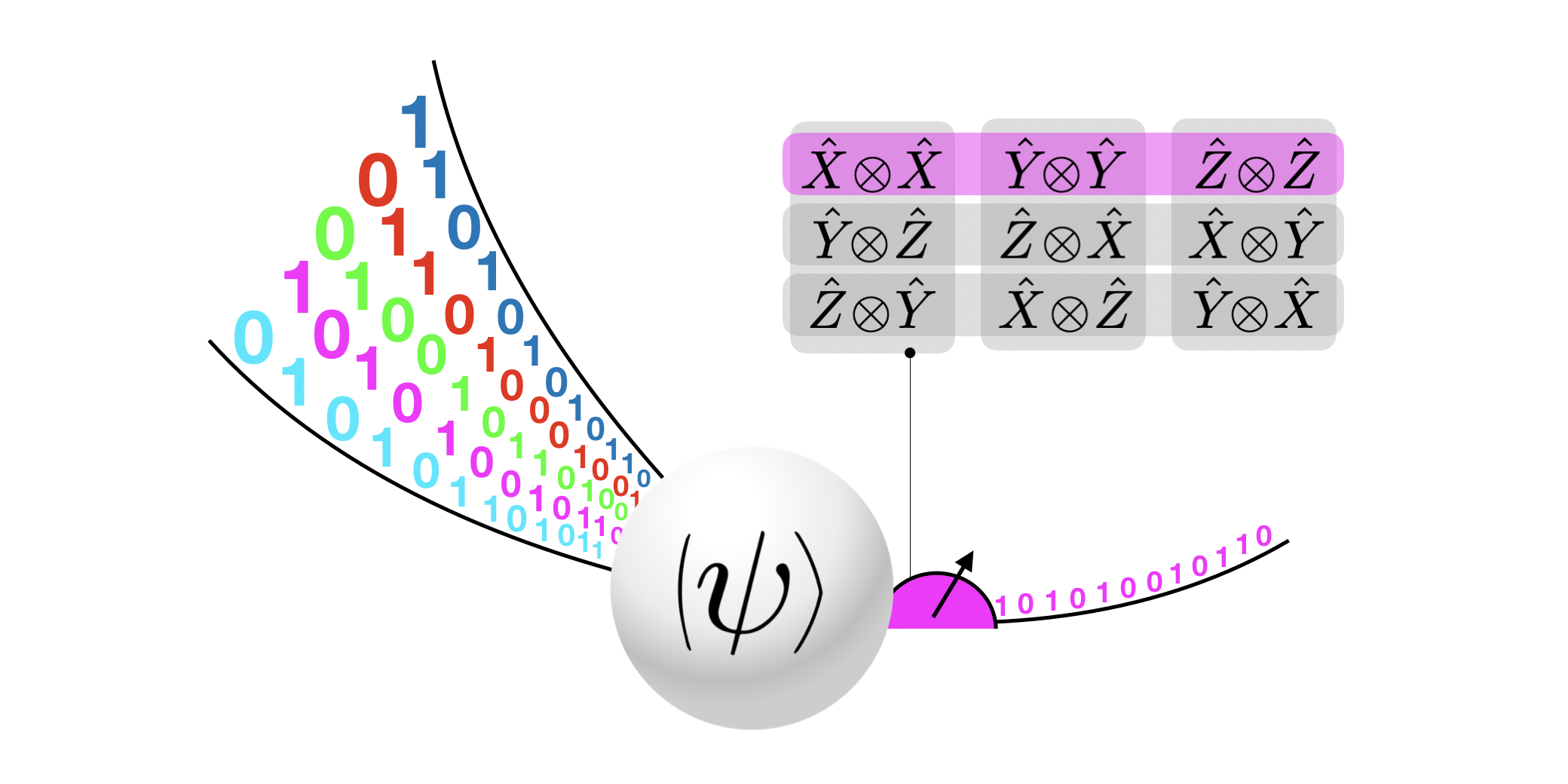
特色图片：量子随机存取码的可视化。经典数据被编码成量子态，并通过在适当的基础上进行测量来检索片段。本文使用的测量基础是由交换多体泡利可观测量集定义的。

热门摘要

量子随机存取码（QRAC）将大量比特存储到更少的量子比特中，与传统的对应物相比，显示出更好的检索成功概率。为此，这些位被映射到量子态，并且每个位都与一种量子测量相关联，稍后可以执行该测量来检索它。这些测量基准通常被选择为相互公正的。

在本文中，我们建议使用相互偏置的测量基，以便每个比特出现在多个测量基中。这不但没有带来缺点，反而使我们能够使用最方便的基础对每个比特进行编码，从而为大规模量子系统节省资源。我们使用多体泡利可观测量来表达我们的比特，并且可以构造的每组通勤可观测量定义一个测量基础。使用 $n$ 量子位系统，此方法展示了 $O(n^2/2^n)$ 的渐近压缩比，并且比之前的 $n ge 16$ 的 QRAC 具有更好的成功概率。

►BibTeX数据

►参考

[1] C. E. Shannon，通信的数学理论，贝尔系统技术期刊 27, 379–423 (1948)。
https：///doi.org/10.1002/j.1538-7305.1948.tb01338.x

[2] W. C. Huffman 和 V. Pless，纠错码基础知识（剑桥大学出版社，2012 年）。

[3] H. Al-Bahadili，一种基于纠错汉明码的新型无损数据压缩方案，计算机与数学与应用 56, 143–150 (2008)。
https://doi.org/10.1016/j.camwa.2007.11.043

[4] A. R. Calderbank 和 P. W. Shor，存在良好的量子纠错码，Phys。修订版 A 54, 1098–1105 (1996)。
https：/ / doi.org/ 10.1103 / PhysRevA.54.1098

[5] A. M. Steane，量子理论中的纠错码，物理学。莱特牧师。 77、793–797（1996）。
https：/ / doi.org/ 10.1103 / PhysRevLett.77.793

[6] L. A. Rozema、D. H. Mahler、A. Hayat、P. S. Turner 和 A. M. Steinberg，量子位系综的量子数据压缩，Phys。莱特牧师。 113, 160504 (2014)。
https：/ / doi.org/ 10.1103 / PhysRevLett.113.160504

[7] D. Gottesman，量子汉明界饱和的量子纠错码类，物理学。修订版 A 54，1862–1868 (1996)。
https：/ / doi.org/ 10.1103 / PhysRevA.54.1862

[8] A. Y. Kitaev，任意子的容错量子计算，物理学年鉴 303，2-30 (2003)。
https:/​/​doi.org/​10.1016/​S0003-4916(02)00018-0

[9] A. Peres，量子理论：概念和方法（Springer Science & Business Media，2006）。

[10] C. H. Bennett、G. Brassard、C. Crépeau、R. Jozsa、A. Peres 和 W. K. Wootters，通过双经典通道和爱因斯坦-波多尔斯基-罗森通道传送未知量子态，物理学。莱特牧师。 70、1895（1993）。
https：/ / doi.org/ 10.1103 / PhysRevLett.70.1895

[11] C. H. Bennett 和 S. J. Wiesner，通过爱因斯坦-波多尔斯基-罗森态上的一粒子和两粒子算子进行通信，物理学。莱特牧师。 69、2881（1992）。
https：/ / doi.org/ 10.1103 / PhysRevLett.69.2881

[12] C. H. Bennett、P. W. Shor、J. A. Smolin 和 A. V. Thapliyal，量子通道的纠缠辅助容量和逆香农定理，IEEE 信息论交易 48.10, 2637–​​2655 (2002)。
https：///doi.org/10.1109/TIT.2002.802612

[13] S. Wiesner，共轭编码，ACM Sigact News 15(1), 78–88 (1983)。
https：/ / doi.org/10.1145/ 1008908.1008920

[14] A. Ambainis、A. Nayak、A. Ta-Shma 和 U. Vazirani，《密集量子编码和单向量子自动机的下界》，载于第 1 届 ACM 计算理论年度研讨会论文集（1999 年）第 376–383 页。
https：/ / doi.org/10.1145/ 301250.301347

[15] A. Ambainis、A. Nayak、A. Ta-Shma 和 U. Vazirani，密集量子编码和量子有限自动机，ACM 杂志 (JACM) 49(4), 496–511 (2002)。
https：/ / doi.org/10.1145/ 581771.581773

[16] M. Pawłowski 和 M. Żukowski，纠缠辅助随机访问码，物理学。修订版 A 81, 042326 (2010)。
https：/ / doi.org/ 10.1103 / PhysRevA.81.042326

[17] A. Casaccino、E. F. Galvão 和 S. Severini，离散维格纳函数和应用的极值，物理学。修订版 A 78, 022310 (2008)。
https：/ / doi.org/ 10.1103 / PhysRevA.78.022310

[18] A. Tavakoli、A. Hameedi、B. Marques 和 M. Bourennane，使用单 d 级系统的量子随机接入码，Phys。莱特牧师。 114, 170502 (2015)。
https：/ / doi.org/ 10.1103 / PhysRevLett.114.170502

[19] J. Pauwels、S. Pironio、E. Woodhead 和 A. Tavakoli，准备和测量场景中的几乎 qudits，Phys。莱特牧师。 129, 250504 (2022)。
https：/ / doi.org/ 10.1103 / PhysRevLett.129.250504

[20] W. K. Wootters 和 B. D. Fields，通过相互无偏测量的最优状态确定，物理学年鉴 191(2), 363–381 (1989)。
https:/​/​doi.org/​10.1016/​0003-4916(89)90322-9

[21] A. Ambainis、D. Leung、L. Mancinska 和 M. Ozols，具有共享随机性的量子随机访问码，arXiv 0810.2937 (2009)。
https://doi.org/10.48550/arXiv.0810.2937

[22] MA Nielsen和IL Chuang，《量子计算和量子信息》（剑桥大学出版社，2010年）。

[23] S. Cheng、J. Chen 和 L. Wang，概率建模的信息视角：玻尔兹曼机与玻恩机，Entropy 20, 583 (2018)。
https：///doi.org/10.3390/e20080583

[24] F. Lardinois，Google Drive 本周将达到 2018 亿用户，TechCrunch (XNUMX)。
https://techcrunch.com/2018/07/25/google-drive-will-hit-a-billion-users-this-week/​

[25] J. Tromp，约翰的国际象棋游乐场，（2010）。
https://tromp.github.io/chess/chess.html

[26] A. Levinovitz，《围棋之谜，计算机仍然无法获胜的古老游戏》，《连线商业》(2014)。
https://www.wired.com/2014/05/the-world-of-computer-go/​

被引用

该论文发表在《量子》杂志上 国际知识共享署名署名4.0（CC BY 4.0） 执照。 版权归原始版权持有者所有，例如作者或其所在机构。

时间戳记：

更多来自 量子杂志