量子相空间的持续专业化

量子相空间的持续专业化

时间戳：24年2023月7日39:XNUMX AM
源节点： 2674950

扎卡里范赫斯特拉滕1,2, 迈克尔·贾布尔1,3,4, 和 Nicolas J. Cerf1

1布鲁塞尔理工学院量子信息和通信中心，CP 165/59，布鲁塞尔自由大学，1050 布鲁塞尔，比利时
2怀恩特光学科学学院，亚利桑那大学，1630 E. University Blvd., Tucson, AZ 85721, USA
3DAMTP，剑桥大学数学科学中心，剑桥 CB3 0WA，英国
4丹麦技术大学物理系，2800 Kongens Lyngby，丹麦

觉得本文有趣或想讨论？ 在SciRate上发表评论或发表评论.

抽象

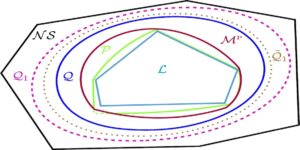
我们探讨了主要化理论在量子相空间中的作用。 为此，我们将自己限制在具有正 Wigner 函数的量子态，并表明连续版本的主要化理论提供了一种优雅且非常自然的方法来探索相空间中 Wigner 函数的信息论性质。 在将所有高斯纯态确定为连续主化的精确意义上的等价物（可以根据哈德逊定理来理解）之后，我们推测出一个基本的主化关系：任何正维格纳函数都被高斯纯态的维格纳函数（尤其是，谐振子的玻色子真空态或基态）。 因此，Wigner 函数的任何 Schur 凹函数的下界都由它为真空态所取的值所限制。 这反过来意味着维格纳熵的下限受其真空态值的限制，而相反的情况显然不成立。 然后，我们的主要结果是为维格纳正量子态的相关子集证明这种基本的主要化关系，这些量子态是谐振子的三个最低本征态的混合。 除此之外，该猜想也得到了数字证据的支持。 最后，我们在相空间熵不确定性关系的背景下讨论了该猜想的一些含义。

热门摘要

不确定性原理是量子物理学中最引人入胜的现象之一。 虽然可以同时准确预测成对的可测量量（例如粒子的位置和动量）似乎很自然，但量子物理学实际上禁止对非通勤可观察量进行此操作。 海森堡和肯纳德通过使用任何可测量量的方差来捕捉其不确定性，从而使这一点变得精确。 多年后，海森堡的不确定性原理被重新表述，将熵作为量化不确定性的适当方法。 在这里，我们引入了一个更强大的信息理论范式来理解相空间中量子变量的不确定性，即主要化理论。

这个数学理论在一个多世纪以前就已经发展起来，并已被用于从统计学到物理学的众多科学领域。 值得注意的是，它最近才被应用于量子物理学，在那里它被证明是探索量子纠缠的有效方法。 因此，它从未被用来表征描述相空间中量子变量的连续密度，即维格纳函数。 我们证明持续专业化是一个合适的工具。 我们论文的主旨是玻色子模式（即谐振子的基态）的真空态的维格纳函数连续主要化任何其他维格纳函数，使其在主要化意义上的不确定性较小.

当我们在量子光学的背景下公开和讨论我们的结果时，它们会延续到任何规范对，因此应该对物理学的各个领域产生影响。

►BibTeX数据

►参考

[1] GH Hardy、JE Littlewood 和 G. Pólya，“不平等”。 剑桥大学出版社，1934 年。
https：/ / doi.org/10.2307/ 3605504

[2] AW Marshall、I. Olkin 和 BC Arnold，“不等式：主要化理论及其应用”，卷。 143. 斯普林格，第二版，2011 年。
https:/​/​doi.org/​10.1007/​978-0-387-68276-1

[3] T. Ando，“主化、双随机矩阵和特征值比较”，线性代数应用。 118, 163–248 (1989)。
https:/​/​doi.org/​10.1016/​0024-3795(89)90580-6

[4] K. Mosler，“Majorization in economic disparity measures”，线性代数及其应用 199, 91–114 (1994)。
https:/​/​doi.org/​10.1016/​0024-3795(94)90343-3

[5] T. van Erven 和 P. Harremoës，“Rényi divergence and majorization”，2010 年 IEEE 信息论国际研讨会，第 1335-1339 页，IEEE。 2010.
https：/ / doi.org/ 10.1109 / ISIT.2010.5513784

[6] MA Alhejji 和 G. Smith，“A Tight Uniform Continuity Bound for Equivocation”，2020 年 IEEE 信息论国际研讨会 (ISIT)，第 2270-2274 页。 2020.
https：/ / doi.org/ 10.1109 / ISIT44484.2020.9174350

[7] MG Jabbour 和 N. Datta，“Arimoto-Rényi 条件熵的紧密一致连续性及其对经典量子态的扩展”，IEEE 信息论汇刊 68，2169–2181 (2022)。
https：///doi.org/10.1109/TIT.2022.3142812

[8] A. Horn，“双重随机矩阵和旋转矩阵的对角线”，美国数学杂志 76, 620–630 (1954)。
https：/ / doi.org/10.2307/ 2372705

[9] MA Nielsen，“一类纠缠转换的条件”，Physical Review Letters 83, 436 (1999)。
https：/ / doi.org/ 10.1103 / PhysRevLett.83.436

[10] MA Nielsen 和 G. Vidal，“Majorization and the interconversion of bipartite states”，Quantum Information and Computation 1, 76–93 (2001)。
https：///doi.org/10.26421/QIC1.1-5

[11] MA Nielsen 和 J. Kempe，“Separable States Are More Disordered Globally than Locally,” Physical Review Letters 86, 5184–5187 (2001)。
https：/ / doi.org/ 10.1103 / PhysRevLett.86.5184

[12] T. Hiroshima，“二分量子态可蒸馏性的主要化标准”，Physical Review Letters 91，057902 (2003)。
https：/ / doi.org/ 10.1103 / PhysRevLett.91.057902

[13] Z. Puchała, Ł. Rudnicki 和 K. Życzkowski，“Majorization entropic uncertainty relations”，Journal of Physics A：Mathematical and Theoretical 46, 272002 (2013)。
https:/​/​doi.org/​10.1088/​1751-8113/​46/​27/​272002

[14] L. Rudnicki、Z. Puchała 和 K. Życzkowski，“强量化熵不确定关系”，Physical Review A 89, 052115 (2014)。
https：/ / doi.org/ 10.1103 / PhysRevA.89.052115

[15] L. Rudnicki，“粗粒度观测值熵不确定性关系的主要化方法”，Physical Review A 91, 032123 (2015)。
https：/ / doi.org/ 10.1103 / PhysRevA.91.032123

[16] F. Brandão、M. Horodecki、N. Ng、J. Oppenheim 和 S. Wehner，“量子热力学第二定律”，美国国家科学院院刊 112，3275–3279 (2015)。
https：/ / doi.org/ 10.1073 / pnas.1411728112

[17] R. García-Patrón、C. Navarrete-Benlloch、S. Lloyd、JH Shapiro 和 NJ Cerf，“高斯通道最小熵猜想的主要化理论方法”，物理评论快报 108，110505 (2012)。
https：/ / doi.org/ 10.1103 / PhysRevLett.108.110505

[18] CN Gagatsos、O. Oreshkov 和 NJ Cerf，“分束器中的主要化关系和纠缠生成”，Physical Review A 87, 042307 (2013)。
https：/ / doi.org/ 10.1103 / PhysRevA.87.042307

[19] G. De Palma、D. Trevisan 和 V. Giovannetti，“被动状态优化玻色子高斯量子通道的输出”，IEEE 信息论汇刊 62，2895–2906 (2016)。
https：///doi.org/10.1109/TIT.2016.2547426

[20] MG Jabbour、R. García-Patrón 和 NJ Cerf，“高斯玻色子通道的主要化保存”，新物理学杂志 18，073047 (2016)。
https:/​/​doi.org/​10.1088/​1367-2630/​18/​7/​073047

[21] MG Jabbour 和 NJ Cerf，“Fock 在被动环境下的玻色子量子通道专业化”，物理学杂志 A：数学和理论 52, 105302 (2019)。
https:/​/​doi.org/​10.1088/​1751-8121/​aaf0d2

[22] U. Leonhardt，“基本量子光学：从量子测量到黑洞”。 剑桥大学出版社，2010 年。
https：/ / doi.org/ 10.1017 / CBO9780511806117

[23] A. Hertz、MG Jabbour 和 NJ Cerf，“熵-幂不确定性关系：对所有高斯纯态的严格不等式”，物理学杂志 A：数学和理论 50, 385301 (2017)。
https：///doi.org/10.1088/1751-8121/aa852f

[24] A. Hertz 和 NJ Cerf，“连续变量熵不确定关系”，物理学杂志 A：数学和理论 52，173001（2019 年）。
https:/​/​doi.org/​10.1088/​1751-8121/​ab03f3

[25] C. Weedbrook、S. Pirandola、R. García-Patrón、NJ Cerf、TC Ralph、JH Shapiro 和 S. Lloyd，“高斯量子信息”，现代物理学评论 84，621–669 (2012)。
https：/ / doi.org/ 10.1103 / RevModPhys.84.621

[26] Z. Van Herstraeten 和 NJ Cerf，“量子维格纳熵”，Physical Review A 104，042211 (2021)。
https：/ / doi.org/ 10.1103 / PhysRevA.104.042211

[27] FJ Narcowich，“Distributions of $hbar$-positive type and applications,” Journal of mathematical physics 30, 2565–2573 (1989).
https：/ / doi.org/10.1063/ 1.528537

[28] T. Bröcker 和 R. Werner，“具有正 Wigner 函数的混合态”，《数学物理学杂志》36、62–75（1995 年）。
https：/ / doi.org/10.1063/ 1.531326

[29] RL Hudson，“Wigner 准概率密度何时为非负？”，数学物理报告 6，249-252（1974）。
https:/​/​doi.org/​10.1016/​0034-4877(74)90007-X

[30] F. Soto 和 P. Claverie，“多维系统的 Wigner 函数何时是非负的？”，数学物理杂志 24，97-100（1983）。
https：/ / doi.org/10.1063/ 1.525607

[31] FJ Narcowich 和 R. O'Connell，“相空间函数成为 Wigner 分布的充分必要条件”，Physical Review A 34, 1 (1986)。
https：/ / doi.org/ 10.1103 / PhysRevA.34.1

[32] A. Mandilara、E. Karpov 和 NJ Cerf，“将 Hudson 定理扩展到混合量子态”，Physical Review A 79, 062302 (2009)。
https：/ / doi.org/ 10.1103 / PhysRevA.79.062302

[33] A. Mandilara、E. Karpov 和 N. Cerf，“具有正维格纳函数的量子混合态的高斯界”，在物理学杂志：会议系列，卷。 254，页。 012011，IOP 出版。 2010.
https:/​/​doi.org/​10.1088/​1742-6596/​254/​1/​012011

[34] L. Wang 和 M. Madiman，“通过重排超越熵幂不等式”，IEEE Transactions on Information Theory 60, 5116–5137 (2014)。
https：///doi.org/10.1109/TIT.2014.2338852

[35] GH Hardy、JE Littlewood 和 G. Pólya，“凸函数满足的一些简单不等式”，Messenger of Mathematics 58, 145–152 (1929)。

[36] H. Joe，“k 元组分布的依赖排序及其在乐透游戏中的应用”，加拿大统计杂志 15, 227–238 (1987)。
https：/ / doi.org/10.2307/ 3314913

[37] I. Schur，“Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten”，Sitzungsberichte der Berliner Mathematischen Gesellschaft 22, 416–427 (1923)。

[38] AW Roberts 和 DE Varberg，“凸函数”。 纽约学术出版社，1973 年。
https:/​/​doi.org/​10.1016/​B978-0-444-89597-4.50013-5

[39] A. Rényi，“关于熵和信息的度量”，第四届伯克利数理统计和概率研讨会论文集，第 1 卷：对统计理论的贡献，第 4 卷。 547，第 562-1961 页，加州大学出版社。 XNUMX.

[40] Y. He、AB Hamza 和 H. Krim，“用于稳健图像配准的广义发散度量”，IEEE 信号处理汇刊 51, 1211–1220 (2003)。
https:// / doi.org/ 10.1109/ TSP.2003.810305

[41] JV Ryff，“双随机变换下 $L^1$ 函数的轨道”，美国数学学会会刊 117, 92–100 (1965)。
https：/ / doi.org/10.2307/ 1994198

[42] F. Bahrami、SM Manjegani 和 S. Moein，“半双重随机算子和可积函数的主要化”，马来西亚数学科学学会公报 44, 693–703 (2021)。
https:/​/​doi.org/​10.1007/​s40840-020-00971-2

[43] SM Manjegani 和 S. Moein，“$ L^{1}(X)$ 上的主要化和半双重随机算子”，《不等式与应用杂志》2023 年，1-20 (2023)。
https：/ / doi.org/ 10.1186 / s13660-023-02935-z

[44] I. Białynicki-Birula 和 J. Mycielski，“波动力学中信息熵的不确定关系，”数学物理通讯 44，129–132（1975 年）。
https：/ / doi.org/ 10.1007 / BF01608825

[45] A. Wehrl，“熵的一般性质”，现代物理学评论 50, 221 (1978)。
https：/ / doi.org/ 10.1103 / RevModPhys.50.221

[46] EH Lieb，“Wehrl 熵猜想的证明”，载于不等式，第 359-365 页。 施普林格，2002 年。
https:/​/​doi.org/​10.1007/​978-3-642-55925-9_30

[47] EH Lieb 和 JP Solovej，“Bloch 相干自旋态及其推广的熵猜想的证明”，Acta Mathematica 212, 379 (2014)。
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[48] JR Johansson、PD Nation 和 F. Nori，“QuTiP：开放量子系统动力学的开源 Python 框架”，计算机物理通讯 183、1760–1772 (2012)。
https：///doi.org/10.1016/j.cpc.2012.02.021

[49] K. Życzkowski、P. Horodecki、A. Sanpera 和 M. Lewenstein，“可分离状态集的体积”，Physical Review A 58, 883 (1998)。
https：/ / doi.org/ 10.1103 / PhysRevA.58.883

被引用

[1] Nuno Costa Dias 和 João Nuno Prata，“关于 Z. Van Herstraeten 和 NJ Cerf 最近对量子维格纳熵的猜想”， 的arXiv：2303.10531, (2023).

[2] Zacharie Van Herstraeten 和 Nicolas J. Cerf，“量子维格纳熵”， 物理评论A 104 4，042211（2021）.

[3] Martin Gärttner、Tobias Haas 和 Johannes Noll，“使用 $Q$ 分布检测相空间中的连续变量纠缠”， 的arXiv：2211.17165, (2022).

以上引用来自 SAO / NASA广告 （最近成功更新为2023-05-24 23:55:18）。 该列表可能不完整，因为并非所有发布者都提供合适且完整的引用数据。

On Crossref的引用服务 找不到有关引用作品的数据（上一次尝试2023-05-24 23:55:17）。

该论文发表在《量子》杂志上 国际知识共享署名署名4.0（CC BY 4.0） 执照。 版权归原始版权持有者所有，例如作者或其所在机构。

时间戳记：

更多来自 量子杂志