Random access-koder via kvantkontextuell redundans

Random access-koder via kvantkontextuell redundans

Tidsstämpel: 13 januari 2023 6:16
Källnod: 1898879

Giancarlo Gatti1,2,3, Daniel Huerga1, Enrique Solano1,4,5,6och Mikel Sanz1,2,5,7

1Institutionen för fysikalisk kemi, Universitetet i Baskien UPV / EHU, Apartado 644, 48080 Bilbao, Spanien
2EHU Quantum Center, Universitetet i Baskien UPV/EHU
3Quantum MADS, Uribitarte Kalea 6, 48001 Bilbao, Spanien
4International Centre of Quantum Artificial Intelligence for Science and Technology (QuArtist) och Institutionen för fysik, Shanghai University, 200444 Shanghai, Kina
5IKERBASQUE, Basque Foundation for Science, Plaza Euskadi 5, 48009 Bilbao, Spanien
6Kipu Quantum, Greifswalderstrasse 226, 10405 Berlin, Tyskland
7Basque Centre for Applied Mathematics (BCAM), Alameda de Mazarredo 14, 48009 Bilbao, Baskien, Spanien

Hitta det här uppsatsen intressant eller vill diskutera? Scite eller lämna en kommentar på SciRate.

Abstrakt

Vi föreslår ett protokoll för att koda klassiska bitar i mätstatistiken för observerbara Pauli-objekt med många kroppar, vilket utnyttjar kvantkorrelationer för en direktåtkomstkod. Mätkontexter byggda med dessa observerbara värden ger resultat med inneboende redundans, något vi utnyttjar genom att koda data till en uppsättning bekväma kontextegentillstånd. Detta gör det möjligt att slumpmässigt komma åt den kodade datan med få resurser. Egentillstånden som används är mycket intrasslade och kan genereras av en diskret parametriserad kvantkrets med lågt djup. Tillämpningar av detta protokoll inkluderar algoritmer som kräver stor datalagring med endast partiell hämtning, vilket är fallet med beslutsträd. Genom att använda $n$-qubit-tillstånd har denna Quantum Random Access Code större sannolikhet för framgång än sin klassiska motsvarighet för $nge 14$ och än tidigare Quantum Random Access-koder för $n ge 16$. Dessutom, för $nge 18$, kan det förstärkas till ett nästan förlustfritt komprimeringsprotokoll med framgångsannolikhet $0.999$ och kompressionsförhållande $O(n^2/2^n)$. Datan den kan lagra är lika med Google-Drive-serverkapaciteten för $n= 44$ och en brute-force-lösning för schack (vad man ska göra på valfri brädkonfiguration) för $n=100$.

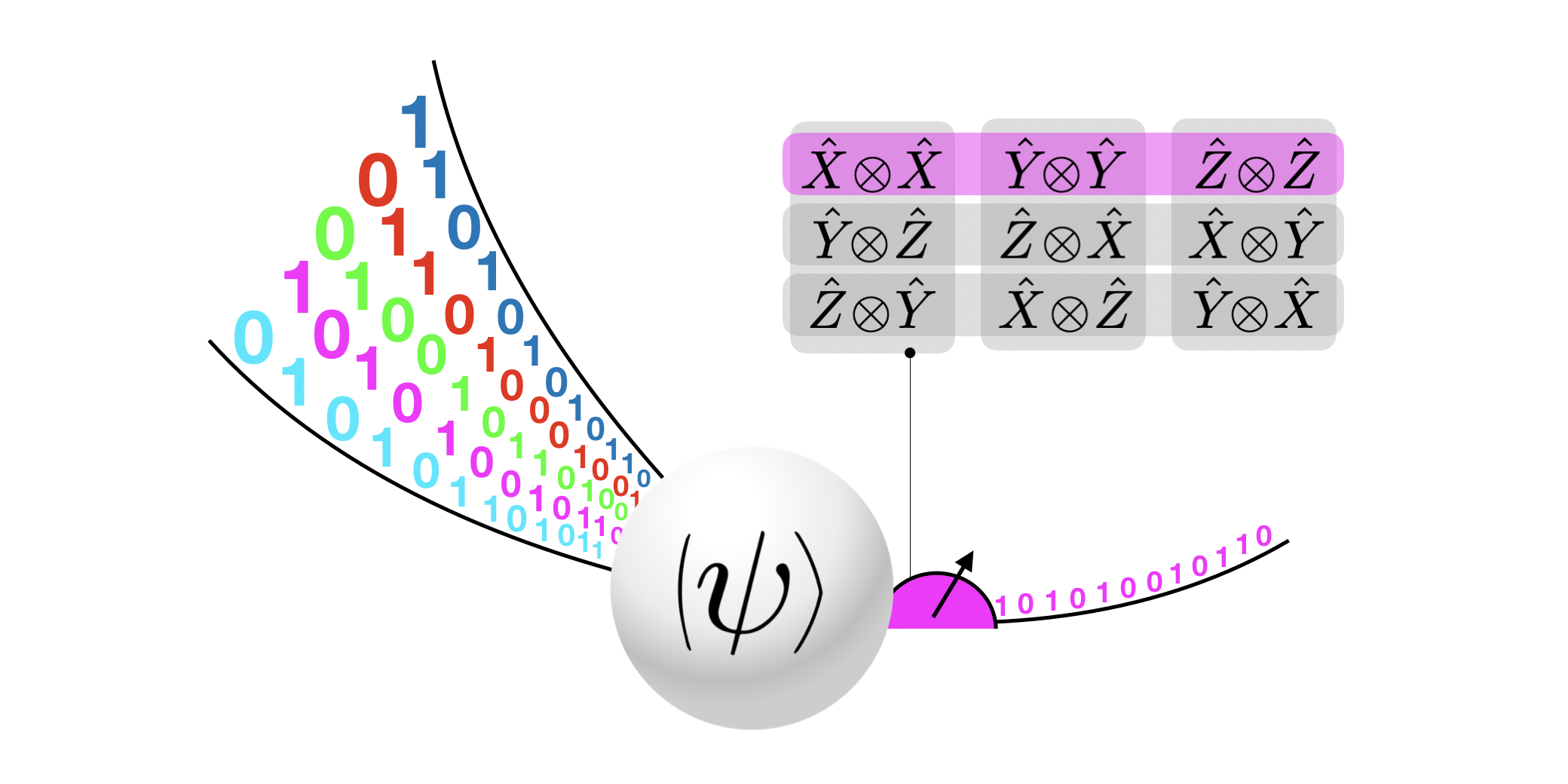
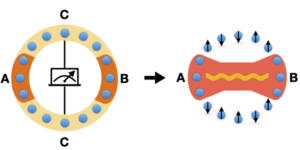
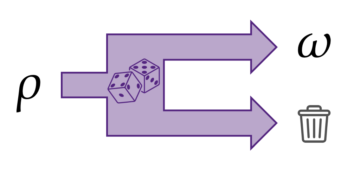
Utvald bild: Visualisering av en Quantum Random Access Code. Klassisk data kodas till ett kvanttillstånd, och ett fragment hämtas genom att mäta i en lämplig bas. Mätbaserna som används i denna artikel definieras av uppsättningar av Pauli-observbara pendlingsobjekt med många kroppar.

Populär sammanfattning

Quantum Random Access Codes (QRAC) lagrar ett antal bitar i färre qubits, vilket visar bättre sannolikhet för framgång för hämtning än deras klassiska motsvarighet. För att göra detta mappas bitarna till ett kvanttillstånd, och varje bit är associerad med en typ av kvantmätning, som senare kan utföras för att hämta den. Dessa mätbaser väljs vanligtvis för att vara ömsesidigt opartiska.

I det här dokumentet föreslår vi användning av mätbaser som är ömsesidigt partiska istället, så att varje bit visas i flera mätbaser. Istället för att utgöra en nackdel tillåter detta oss att koda varje bit med den mest bekväma grunden, vilket sparar resurser för storskaliga kvantsystem. Vi använder Pauli observerbara objekt med många kroppar för att förmedla våra bitar, och varje uppsättning observerbara pendlingsobjekt som kan konstrueras definierar en mätgrund. Genom att använda system med $n$ qubits visar detta tillvägagångssätt ett asymptotiskt kompressionsförhållande på $O(n^2/2^n)$ och bättre framgångsannolikhet än tidigare QRAC:er för $n ge 16$.

► BibTeX-data

► Referenser

[1] CE Shannon, A matematical theory of communication, The Bell system technical journal 27, 379–423 (1948).
https: / / doi.org/ 10.1002 / j.1538-7305.1948.tb01338.x

[2] WC Huffman och V. Pless, Fundamentals of error-correcting codes (Cambridge University Press, 2012).

[3] H. Al-Bahadili, Ett nytt förlustfritt datakomprimeringsschema baserat på felkorrigering av Hamming-koder, Computers & Mathematics with Applications 56, 143–150 (2008).
https://​/​doi.org/​10.1016/​j.camwa.2007.11.043

[4] AR Calderbank och PW Shor, Bra kvantfelskorrigerande koder finns, Phys. Rev. A 54, 1098-1105 (1996).
https: / / doi.org/ 10.1103 / PhysRevA.54.1098

[5] AM Steane, Felkorrigerande koder i kvantteorin, Phys. Rev. Lett. 77, 793-797 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.793

[6] LA Rozema, DH Mahler, A. Hayat, PS Turner och AM Steinberg, Quantum data compression of a qubit ensemble, Phys. Rev. Lett. 113, 160504 (2014).
https: / / doi.org/ 10.1103 / PhysRevLett.113.160504

[7] D. Gottesman, Class of quantum error-correcting codes saturating the quantum Hamming bound, Phys. Rev. A 54, 1862–1868 (1996).
https: / / doi.org/ 10.1103 / PhysRevA.54.1862

[8] AY Kitaev, Fault-tolerant quantum computation by anyons, Annals of Physics 303, 2–30 (2003).
https:/​/​doi.org/​10.1016/​S0003-4916(02)00018-0

[9] A. Peres, Quantum theory: Concepts and Methods (Springer Science & Business Media, 2006).

[10] CH Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres och WK Wootters, Teleporting av ett okänt kvanttillstånd via dubbla klassiska och Einstein-Podolsky-Rosen-kanaler, Phys. Rev. Lett. 70, 1895 (1993).
https: / / doi.org/ 10.1103 / PhysRevLett.70.1895

[11] CH Bennett och SJ Wiesner, Kommunikation via en- och tvåpartikeloperatörer på Einstein-Podolsky-Rosen-tillstånd, Phys. Rev. Lett. 69, 2881 (1992).
https: / / doi.org/ 10.1103 / PhysRevLett.69.2881

[12] CH Bennett, PW Shor, JA Smolin och AV Thapliyal, Entanglement-assisterad kapacitet för en kvantkanal och omvänd Shannon-satsen, IEEE-transaktioner på Information Theory 48.10, 2637–2655 (2002).
https: / / doi.org/ 10.1109 / TIT.2002.802612

[13] S. Wiesner, Conjugate coding, ACM Sigact News 15(1), 78–88 (1983).
https: / / doi.org/ 10.1145 / 1008908.1008920

[14] A. Ambainis, A. Nayak, A. Ta-Shma och U. Vazirani, Dense quantum coding and a lower bound for 1-way quantum automata, i Proceedings of the trettioförsta årliga ACM symposium on Theory of Computing (1999) s. 376–383.
https: / / doi.org/ 10.1145 / 301250.301347

[15] A. Ambainis, A. Nayak, A. Ta-Shma och U. Vazirani, Dense quantum coding and quantum finite automata, Journal of the ACM (JACM) 49(4), 496–511 (2002).
https: / / doi.org/ 10.1145 / 581771.581773

[16] M. Pawłowski och M. Żukowski, Entanglement-assisted random access codes, Phys. Rev. A 81, 042326 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.042326

[17] A. Casaccino, EF Galvão och S. Severini, Extrema av diskreta Wigner-funktioner och tillämpningar, Phys. Rev. A 78, 022310 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.022310

[18] A. Tavakoli, A. Hameedi, B. Marques och M. Bourennane, Quantum random access codes using single d-level systems, Phys. Rev. Lett. 114, 170502 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502

[19] J. Pauwels, S. Pironio, E. Woodhead och A. Tavakoli, Nästan qudits i förbered-och-mät-scenariot, Phys. Rev. Lett. 129, 250504 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.250504

[20] WK Wootters och BD Fields, Optimal tillståndsbestämning genom ömsesidigt opartiska mätningar, Annals of Physics 191(2), 363–381 (1989).
https:/​/​doi.org/​10.1016/​0003-4916(89)90322-9

[21] A. Ambainis, D. Leung, L. Mancinska och M. Ozols, Quantum random access codes with shared randomness, arXiv 0810.2937 (2009).
https://​/​doi.org/​10.48550/​arXiv.0810.2937

[22] MA Nielsen och IL Chuang, Quantum Computation and Quantum Information (Cambridge University Press, 2010).

[23] S. Cheng, J. Chen och L. Wang, Informationsperspektiv till probabilistisk modellering: Boltzmann-maskiner kontra Born-maskiner, Entropy 20, 583 (2018).
https: / / doi.org/ 10.3390 / e20080583

[24] F. Lardinois, Google Drive kommer att nå en miljard användare den här veckan, TechCrunch (2018).
https://​/​techcrunch.com/​2018/​07/​25/​google-drive-will-hit-a-billion-users-this-week/​

[25] J. Tromp, Johns schacklekplats, (2010).
https://​/​tromp.github.io/​chess/​chess.html

[26] A. Levinovitz, The mystery of Go, det uråldriga spelet som datorer fortfarande inte kan vinna, Wired Business (2014).
https://​/​www.wired.com/​2014/​05/​the-world-of-computer-go/​

Citerad av

Detta papper publiceras i Quantum under Creative Commons Attribution 4.0 International (CC BY 4.0) licens. Upphovsrätten kvarstår med de ursprungliga upphovsrättsinnehavarna som författarna eller deras institutioner.

Tidsstämpel:

Mer från Quantum Journal