Quantum Wasserstein-avstånd baserat på en optimering över separerbara tillstånd

Quantum Wasserstein-avstånd baserat på en optimering över separerbara tillstånd

Tidsstämpel: 16 oktober 2023 10:35
Källnod: 2938953

Géza Tóth1,2,3,4,5 och József Pitrik5,6,7

1Teoretisk fysik, universitetet i Baskien UPV/EHU, ES-48080 Bilbao, Spanien
2EHU Quantum Center, Universitetet i Baskien UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscaya, Spanien
3Donostia International Physics Center (DIPC), ES-20080 San Sebastián, Spanien
4IKERBASQUE, Basque Foundation for Science, ES-48011 Bilbao, Spanien
5Institutet för fasta tillståndets fysik och optik, Wigner Research Center for Physics, HU-1525 Budapest, Ungern
6Alfréd Rényi Institute of Mathematics, Reáltanoda u. 13-15., HU-1053 Budapest, Ungern
7Institutionen för analys och operationsforskning, Matematiska institutet, Budapests tekniska och ekonomiska universitet, Müegyetem rkp. 3., HU-1111 Budapest, Ungern

Hitta det här uppsatsen intressant eller vill diskutera? Scite eller lämna en kommentar på SciRate.

Abstrakt

Vi definierar kvant-Wasserstein-avståndet så att optimeringen av kopplingen utförs över tvådelade separerbara tillstånd snarare än tvådelade kvanttillstånd i allmänhet, och undersöker dess egenskaper. Överraskande nog finner vi att självdistansen är relaterad till kvantinformationen från Fisher. Vi presenterar en transportkarta som motsvarar ett optimalt tvådelat separerbart tillstånd. Vi diskuterar hur det introducerade kvantavståndet Wasserstein är kopplat till kriterier som detekterar kvanttrassling. Vi definierar variansliknande kvantiteter som kan erhållas från kvant-Wasserstein-avståndet genom att ersätta minimeringen över kvanttillstånden med en maximering. Vi utökar våra resultat till en familj av generaliserade kvantum Fisher-informationskvantiteter.

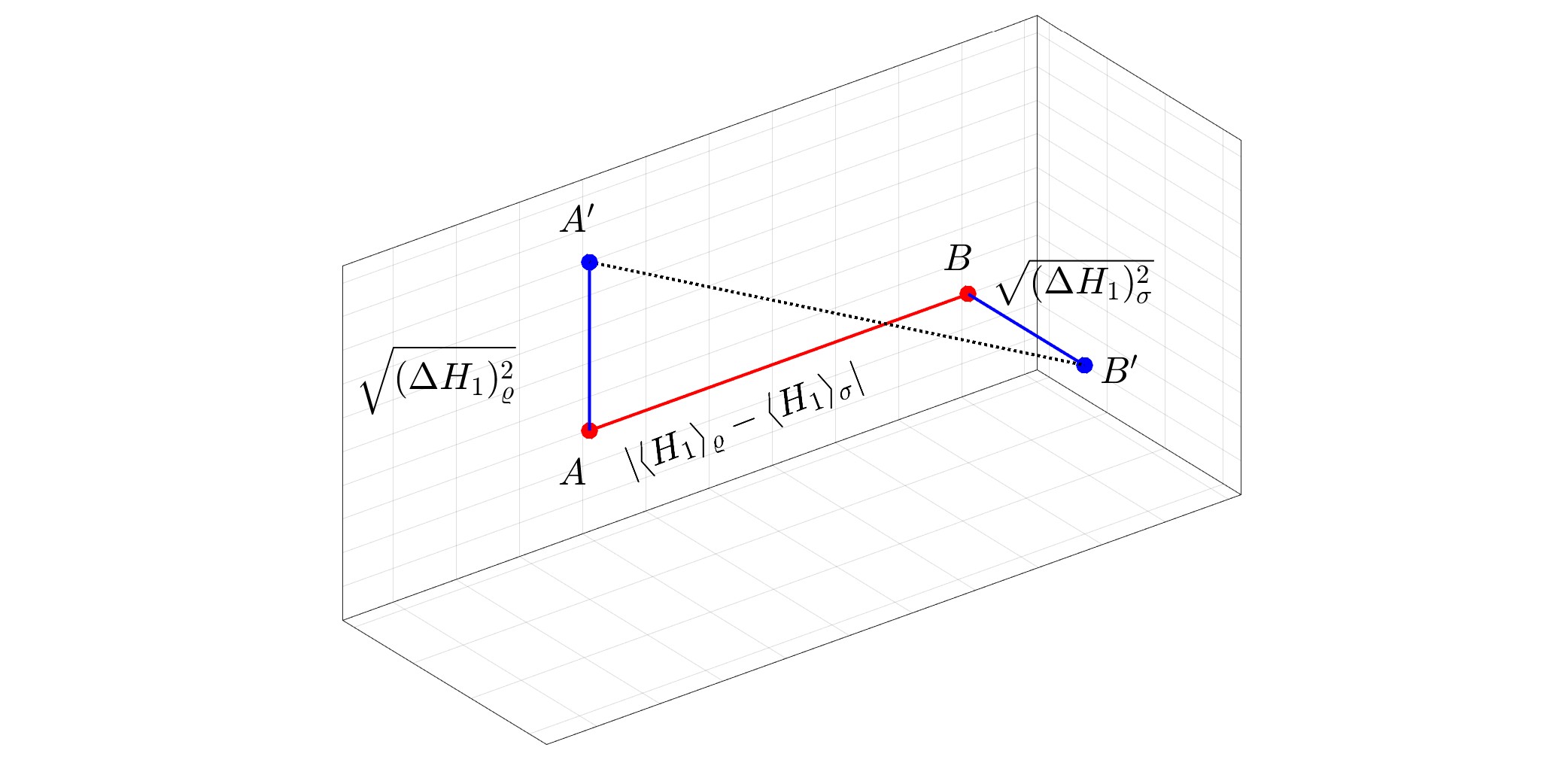
Utvald bild: Geometrisk representation av kvant-Wasserstein-avståndet mellan ett rent tillstånd $varrho$ och ett blandat tillstånd $sigma$ för $N=1.$ Kvant-Wasserstein-avståndet är lika med $1/sqrt2$ gånger det vanliga euklidiska avståndet mellan $A'$ och $B'.$

Populär sammanfattning

I vardagen talar avståndet mellan två städer om hur många kilometer vi måste köra från den ena till den andra. Det går också att karakterisera hur lätt vi kan ta oss från den ena staden till den andra är att mäta bränsleförbrukningen under vår resa. Det senare är mer informativt i den meningen att det återspeglar resans kostnad relaterat till vägens topografi, dvs. det är känsligt för det underliggande måttet. Låt oss sedan föreställa oss att vi behöver flytta en hög med sand från en plats till en annan och den nya högen kan ha en annan form. I detta fall kan vi återigen karakterisera ansträngningen att flytta sanden med kostnaden för transporten.

Avstånd spelar en central roll inom matematik, fysik och teknik. Ett grundläggande problem inom sannolikhet och statistik är att komma på användbara mått på avståndet mellan två sannolikhetsfördelningar. Tyvärr är många föreställningar om avstånd mellan sannolikhetsfördelningar, säg p(x) och q(x), maximala om de inte överlappar varandra, dvs den ena är alltid noll när den andra inte är noll. Detta är opraktiskt för många tillämpningar. Till exempel, för att återgå till sandanalogin, verkar två icke-överlappande högar med sand vara lika långt från varandra, oavsett om deras avstånd är 10 km eller 100 km. Optimal transportteori är ett sätt att konstruera en alternativ föreställning om avstånd mellan sannolikhetsfördelningar, det så kallade Wassersteinavståndet. Det kan vara icke-maximalt även om fördelningarna inte överlappar varandra, det är känsligt för det underliggande måttet (dvs kostnaden för transporten), och i huvudsak uttrycker det den ansträngning vi behöver för att flytta den ena till den andra, som om de vore sandkullar.

Nyligen har kvantavståndet Wasserstein definierats genom att generalisera det klassiska Wassersteinavståndet. Den är baserad på minimeringen av en kostnadsfunktion över kvanttillstånden i ett tvådelat kvantsystem. Den har egenskapen analog med den som nämns ovan i kvantvärlden. Det kan vara icke-maximalt för ortogonala tillstånd, vilket är användbart, till exempel när vi behöver lära ut kvantdata till en algoritm.

Som vi kan förvänta oss har kvant Wasserstein-avstånd också egenskaper som skiljer sig mycket från dess klassiska motsvarighet. Till exempel, när vi mäter avståndet för ett kvanttillstånd från sig självt, kan det vara likt noll. Även om detta redan är förbryllande, har det också visat sig att självdistansen är relaterad till Wigner-Yanase-skevinformationen, som introducerades 1963 av nobelpristagaren EP Wigner, som har viktiga bidrag till grunderna för kvantfysiken och MM Yanase.

I vår tidning tittar vi på detta mystiska fynd från ännu ett annat håll. Vi begränsar den ovan nämnda minimeringen till så kallade separerbara tillstånd. Dessa är de kvanttillstånd som inte innehåller intrassling. Vi finner att självdistansen blir Fisher-informationen, en kvantitet som är central i kvantmetrologi och kvantuppskattningsteori, och som till exempel förekommer i den berömda Cramer-Rao-bindningen. Genom att undersöka egenskaperna hos ett sådant Wasserstein-avstånd banar vårt arbete väg för att koppla teorin om kvant-Wasserstein-avståndet till teorin om kvantintrassling.

► BibTeX-data

► Referenser

[1] G. Monge. "Mémoire sur la théory des déblais et des remblais". Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L. Kantorovitch. "Om förflyttning av massor". Management Science 5, 1–4 (1958). URL: http://​/​www.jstor.org/​stable/​2626967.
http: / / www.jstor.org/ stabil / 2626967

[3] Emmanuel Boissard, Thibaut Le Gouic och Jean-Michel Loubes. "Distributionens malluppskattning med wasserstein-mått". Bernoulli 21, 740–759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

[4] Oleg Butkovsky. "Subgeometriska konvergenshastigheter för Markov-processer i Wasserstein-metriken". Ann. Appl. Probab. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[5] M. Hairer, J.-C. Mattingly och M. Scheutzow. "Asymptotisk koppling och en allmän form av Harris teorem med tillämpningar på stokastiska fördröjningsekvationer". Probab. Teori Relat. Fields 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[6] M. Hairer och JC Mattingly. "Spektrala luckor i Wasserstein-avstånd och de 2D Stokastiska Navier-Stokes-ekvationerna". Ann. Probab. 36, 2050–2091 (2008).
https://doi.org/ 10.1214/08-AOP392

[7] A. Figalli, F. Maggi och A. Pratelli. "En masstransportmetod för kvantitativa isoperimetriska ojämlikheter". Uppfinna. Matematik. 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli och F. Maggi. "Om formen av flytande droppar och kristaller i den lilla massan". Båge. Ransonera. Mech. Anal. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[9] J. Lott och C. Villani. "Ricci-krökning för metriska mätutrymmen via optimal transport". Ann. av matte. 169 (3), 903–991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

[10] Max-K. von Renesse och Karl-Theodor Sturm. "Transportojämlikheter, gradientuppskattningar, entropi och Ricci-kurvatur". Comm. Ren appl. Matematik. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[11] Karl-Theodor Sturm. "Om geometrin hos metriska måttutrymmen I". Acta Math. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[12] Karl-Theodor Sturm. "Om geometrin för metriska måttutrymmen II". Acta Math. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[13] Benoı̂t Kloeckner. "En geometrisk studie av Wasserstein-utrymmen: Euklidiska utrymmen". Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / ⠀ </ ⠀ <doi.org/†<10.2422 / ⠀ <2036 till 2145.2010.2.03

[14] György Pál Gehér, Tamás Titkos och Dániel Virosztek. "Om isometriska inbäddningar av wasserstein-utrymmen - det diskreta fallet". J. Math. Anal. Appl. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. "Isometrisk studie av Wasserstein-utrymmen - den verkliga linjen". Trans. Amer. Matematik. Soc. 373, 5855–5883 (2020).
https://​/​doi.org/​10.1090/​tran/​8113

[16] György Pál Gehér, Tamás Titkos och Dániel Virosztek. "Isometrigruppen av Wasserstein-rum: det hilbertska fallet". J. Lond. Matematik. Soc. 106, 3865–3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

[17] György Pál Gehér, Tamás Titkos och Dániel Virosztek. "Isometrisk styvhet av wasserstein tori och sfärer". Mathematika 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[18] Gergely Kiss och Tamás Titkos. "Isometrisk styvhet av wasserstein-utrymmen: grafmetriska fallet". Proc. Am. Matematik. Soc. 150, 4083–4097 (2022).
https: / / doi.org/ 10.1090 / proc / 15977

[19] György Pál Gehér, Tamás Titkos och Dániel Virosztek. "Om det exotiska isometriska flödet av det kvadratiska wasserstein-utrymmet över den verkliga linjen". Linjär Algebra Appl. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, SR Park och GK Rohde. "Radon kumulativ distributionstransform och dess tillämpning på bildklassificering". IEEE Trans. Bildprocess. 25, 920–934 (2016).
https://doi.org/ 10.1109/TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek och GK Rohde. "Ett linjärt optimalt transportramverk för att kvantifiera och visualisera variationer i uppsättningar av bilder". Int. J. Comput. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepcev, GK Rohde. "Optimal masstransport: applikationer för signalbehandling och maskininlärning". IEEE Signal Processing Magazine 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

[23] A. Gramfort, G. Peyré och M. Cuturi. "Snabb optimal transportmedelvärde av neuroimagingdata". Informationsbehandling inom medicinsk bildbehandling. IPMI 2015. Lecture Notes in Computer Science 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu och X. Gu. "Formklassificering med Wasserstein-avstånd för analys av hjärnmorfometri". Informationsbehandling inom medicinsk bildbehandling. IPMI 2015. Lecture Notes in Computer Science 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala och Léon Bottou. "Wasserstein generativa kontradiktoriska nätverk". I Doina Precup och Yee Whye Teh, redaktörer, Proceedings of the 34th International Conference on Machine Learning. Volym 70 av Proceedings of Machine Learning Research, sidorna 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] TA El Moselhy och YM Marzouk. "Bayesiansk slutledning med optimala kartor". J. Comput. Phys. 231, 7815–7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022

[27] Gabriel Peyré och Marco Cuturi. "Computational Optimal Transport: With Applications to Data Science". Hittades. Trender maskininlärning. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya och Tomaso A Poggio. "Lärande med en wasserstein förlust". I C. Cortes, N. Lawrence, D. Lee, M. Sugiyama och R. Garnett, redaktörer, Advances in Neural Information Processing Systems. Volym 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[29] A. Ramdas, NG Trillos och M. Cuturi. "Om Wasserstein tvåprovstestning och relaterade familjer av icke-parametriska tester". Entropy 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[30] S. Srivastava, C. Li och DB Dunson. "Skalbar Bayes via Barycenter i Wasserstein Space". J. Mach. Lära sig. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski och Wojeciech Slomczynski. "Monge-avståndet mellan kvanttillstånd". J. Phys. A: Matematik. Gen. 31, 9095-9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[32] Karol Życzkowski och Wojciech Slomczynski. "Monge-metriken om kvanttillståndens sfär och geometri". J. Phys. A: Matematik. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[33] Ingemar Bengtsson och Karol Życzkowski. "Geometri of quantum states: En introduktion till quantum entanglement". Cambridge University Press. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane och D. Voiculescu. "En fri sannolikhetsanalog av Wasserstein-metriken på spårtillståndsutrymmet". GAFA, Geom. Funktion. Anal. 11, 1125–1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[35] Eric A. Carlen och Jan Maas. "En analog av 2-Wasserstein-måttet i icke-kommutativ sannolikhet under vilken den fermioniska Fokker-Planck-ekvationen är gradientflöde för entropin". Commun. Matematik. Phys. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[36] Eric A. Carlen och Jan Maas. "Gradientflöde och entropi ojämlikheter för kvantmarkovsemigrupper med detaljerad balans". J. Funktion. Anal. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

[37] Eric A. Carlen och Jan Maas. "Icke-kommutativ kalkyl, optimal transport och funktionella ojämlikheter i dissipativa kvantsystem". J. Stat. Phys. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

[38] Nilanjana Datta och Cambyse Rouzé. "Koncentration av kvanttillstånd från kvantfunktionella ojämlikheter och transportkostnader". J. Math. Phys. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[39] Nilanjana Datta och Cambyse Rouzé. "Relaterande relativ entropi, optimal transport och Fisher information: A quantum HWI ojämlikhet". Ann. Henri Poincaré 21, 2115–2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[40] François Golse, Clément Mouhot och Thierry Paul. "Om medelfältet och klassiska gränser för kvantmekaniken". Commun. Matematik. Phys. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[41] François Golse och Thierry Paul. "Schrödinger-ekvationen i medelfältet och semiklassisk regim". Båge. Ransonera. Mech. Anal. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[42] François Golse och Thierry Paul. "Vågpaket och det kvadratiska Monge-Kantorovich-avståndet i kvantmekanik". Comptes Rendus Math. 356, 177–197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

[43] François Golse. "Kvantum $N$-kroppsproblemet i medelfältet och semiklassisk regim". Phil. Trans. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse och T. Paul. "Kvantoptimal transport är billigare". J. Stat. Phys. 181, 149–162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[45] Emanuele Caglioti, François Golse och Thierry Paul. "Mot optimal transport för kvanttätheter". arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma och Dario Trevisan. "Kvantoptimal transport med kvantkanaler". Ann. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan och Seth Lloyd. "Quantum Wasserstein distans av ordning 1". IEEE Trans. Inf. Theory 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole och Karol Życzkowski. "Quantum Monge-Kantorovich problem och transportavstånd mellan densitetsmatriser". Phys. Rev. Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland och Karol Życzkowski. "Kvantoptimal transport". arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein och K. Życzkowski. "Monotonicitet för ett kvant 2-Wasserstein-avstånd". J. Phys. A: Matematik. Theor. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos och Dániel Virosztek. "Quantum Wasserstein isometrier på qubit-tillståndsutrymmet". J. Math. Anal. Appl. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe och Seth Lloyd. "Wasserstein komplexitet av kvantkretsar". arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu och Seth Lloyd. "Lära sig kvantdata med kvantjordflyttarens avstånd". Quantum Sci. Technol. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[54] EP:n Wigner och Mutsuo M. Yanase. "Informationsinnehåll i distributioner". Proc. Natl. Acad. Sci. USA 49, 910-918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki och Karol Horodecki. "Kvantsammanflätning". Rev. Mod. Phys. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[56] Otfried Gühne och Géza Tóth. "Intrasslingsdetektering". Phys. Rep. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik och Marcus Huber. "Entanglement-certifiering från teori till experiment". Nat. Rev. Phys. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd och Lorenzo Maccone. "Kvantförstärkta mätningar: Överträffar standardkvantgränsen". Science 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

[59] Matteo GA Paris. "Kvantuppskattning för kvantteknologi". Int. J. Quant. Inf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna och Jan Kolodynski. "Kapitel fyra - Kvantgränser i optisk interferometri". Prog. Optik 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze och Augusto Smerzi. "Kvanteori för fasuppskattning". I GM Tino och MA Kasevich, redaktörer, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Kurs 188, Varenna). Sidorna 691–741. IOS Press, Amsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Géza Tóth och Dénes Petz. "Extrema egenskaper hos variansen och quantum Fisher-informationen". Phys. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[63] Sixia Yu. "Quantum Fisher Information som det konvexa varianstaket". arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

[64] Géza Tóth och Florian Fröwis. "Osäkerhetsrelationer med variansen och kvantinformationen från Fisher baserat på konvexa nedbrytningar av densitetsmatriser". Phys. Rev. Research 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[65] Shao-Hen Chiew och Manuel Gessner. "Förbättring av summaosäkerhetsrelationer med Quantum Fisher-informationen". Phys. Rev. Research 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[66] CW Helström. "Kvantumdetektering och uppskattningsteori". Academic Press, New York. (1976). URL: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[67] AS Holevo. "Probabilistiska och statistiska aspekter av kvantteorin". Nord-Holland, Amsterdam. (1982).

[68] Samuel L. Braunstein och Carlton M. Caves. "Statistiskt avstånd och kvanttillståndens geometri". Phys. Rev. Lett. 72, 3439-3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

[69] Samuel L Braunstein, Carlton M Caves och Gerard J Milburn. "Generaliserade osäkerhetsrelationer: Teori, exempel och Lorentz-invarians". Ann. Phys. 247, 135-173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[70] Dénes Petz. "Kvantinformationsteori och kvantstatistik". Springer, Berlin, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[71] Géza Tóth och Iagoba Apellaniz. "Kvantmetrologi ur ett kvantinformationsvetenskapligt perspektiv". J. Phys. A: Matematik. Theor. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied och Philipp Treutlein. "Kvantmetrologi med icke-klassiska tillstånd av atomensembler". Rev. Mod. Phys. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[73] Marco Barbieri. "Optisk kvantmetrologi". PRX Quantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

[74] Zoltán Léka och Dénes Petz. "Några nedbrytningar av matrisvariationer". Probab. Matematik. Statistik. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Dénes Petz och Dániel Virosztek. "En karakteriseringssats för matrisvarianser". Acta Sci. Matematik. (Szeged) 80, 681–687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

[76] Akio Fujiwara och Hiroshi Imai. "Ett fiberknippe över mängder av kvantkanaler och dess tillämpning på kvantstatistik". J. Phys. A: Matematik. Theor. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[77] BM Escher, RL de Matos Filho och L. Davidovich. "Allmänt ramverk för att uppskatta den ultimata precisionsgränsen i bullrig kvantförstärkt metrologi". Nat. Phys. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński och Mădălin Guţă. "Den svårfångade Heisenberg-gränsen i kvantförstärkt metrologi". Nat. Commun. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[79] Iman Marvian. "Operationell tolkning av kvantfiskarinformation i kvanttermodynamik". Phys. Rev. Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

[80] Reinhard F. Werner. "Kvanttillstånd med Einstein-Podolsky-Rosen-korrelationer som medger en dold-variabel modell". Phys. Rev. A 40, 4277-4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss och M. Lewenstein. "Kvantkorrelationer i system av oskiljbara partiklar". Ann. Phys. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui och Nobuhiro Yonezawa. "Utbytessymmetri och flerdelad intrassling". Phys. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[83] Pawel Horodecki. "Separerbarhetskriterium och oskiljaktiga blandade tillstånd med positiv partiell införlivande". Phys. Lett. A 232, 333-339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[84] Asher Peres. "Separerbarhetskriterium för densitetsmatriser". Phys. Rev. Lett. 77, 1413-1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki och Ryszard Horodecki. "Bunden intrassling kan aktiveras". Phys. Rev. Lett. 82, 1056-1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

[86] Géza Tóth och Tamás Vértesi. "Kvanttillstånd med positiv partiell transponering är användbara för metrologi". Phys. Rev. Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

[87] Scott Hill och William K. Wootters. "Intrassling av ett par kvantbitar". Phys. Rev. Lett. 78, 5022-5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

[88] William K. Wootters. "Entanglement av bildning av ett godtyckligt tillstånd av två qubits". Phys. Rev. Lett. 80, 2245-2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal och Armin Uhlmann. "Inträngning av hjälp". quant-ph/​9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: kvant-ph / 9803033

[90] John A. Smolin, Frank Verstraete och Andreas Winter. "Inträngning av bistånd och multipartstatlig destillation". Phys. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[91] Holger F. Hofmann och Shigeki Takeuchi. "Brott mot lokala osäkerhetsrelationer som ett tecken på förveckling". Phys. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[92] Otfried Gühne. "Karakteriserande förveckling via osäkerhetsrelationer". Phys. Rev. Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth och Peter Adam. "Intrasslingskriterier baserade på lokala osäkerhetsrelationer är strikt starkare än det beräkningsbara korsnormkriteriet". Phys. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza och Géza Tóth. "Snurr som pressar ojämlikheter för godtycklig spinn". Phys. Rev. Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

[95] AR Edmonds. "Vinkelmomentum i kvantmekanik". Princeton University Press. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[96] Géza Tóth. "Entanglement detektion i optiska gitter av bosoniska atomer med kollektiva mätningar". Phys. Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne och Hans J. Briegel. "Optimala spinnklämmande ojämlikheter upptäcker bunden intrassling i spinnmodeller". Phys. Rev. Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

[98] Géza Tóth och Morgan W Mitchell. "Generering av makroskopiska singletttillstånd i atomära ensembler". New J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[99] Géza Tóth. "Detektering av multipartit intrassling i närheten av symmetriska Dicke-tillstånd". J. Opt. Soc. Am. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

[100] Géza Tóth, Tobias Moroder och Otfried Gühne. "Utvärdering av åtgärder för konvexa tak intrassling". Phys. Rev. Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

[101] Lieven Vandenberghe och Stephen Boyd. "Halvbestämd programmering". SIAM Review 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[102] Géza Tóth. "Flerpartsförveckling och högprecisionsmätning". Phys. Rev. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé och Augusto Smerzi. "Fisher information och multiparticle intrassling". Phys. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki och Ryszard Horodecki. "Aktivera dold metrologisk användbarhet". Phys. Rev. Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo och Federico M. Spedalieri. "Särskilja separerbara och intrasslade tillstånd". Phys. Rev. Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo och Federico M. Spedalieri. "Komplett familj av separerbarhetskriterier". Phys. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo och Federico M. Spedalieri. "Upptäcker flerpartsintrassling". Phys. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[108] Harold Ollivier och Wojciech H. Zurek. "Quantum discord: Ett mått på kvantiteten av korrelationer". Phys. Rev. Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

[109] L. Henderson och V. Vedral. "Klassiska, kvant- och totala korrelationer". J. Phys. A: Matematik. Gen. 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[110] Anindita Bera, Tamogna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) och Ujjwal Sen. "Quantum discord and its allies: a review of recent progress". Rep. Prog. Phys. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

[111] Dénes Petz. "Kovarians och Fisher-information i kvantmekanik". J. Phys. A: Matematik. Gen. 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[112] Paolo Gibilisco, Fumio Hiai och Dénes Petz. "Quantum kovarians, quantum Fisher information och osäkerhetsrelationer". IEEE Trans. Inf. Theory 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[113] D. Petz och C. Ghinea. "Introduktion till quantum Fisher information". Volym 27, sidorna 261–281. World Scientific. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[114] Frank Hansen. "Metrisk justerad snedställningsinformation". Proc. Natl. Acad. Sci. USA 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami och Frank Hansen. "Ett enhetligt tillvägagångssätt för lokal kvantosäkerhet och interferometrisk kraft genom metrisk justerad skevningsinformation". Entropy 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[116] MATLAB. "9.9.0.1524771(r2020b)". The MathWorks Inc. Natick, Massachusetts (2020).

[117] MOSEK ApS. “MOSEK optimeringsverktygslådan för MATLAB manual. Version 9.0". (2019). URL: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[118] J. Löfberg. "YALMIP: En verktygslåda för modellering och optimering i MATLAB". I handlingar från CACSD-konferensen. Taipei, Taiwan (2004).

[119] Géza Tóth. "QUBIT4MATLAB V3.0: Ett programpaket för kvantinformationsvetenskap och kvantoptik för MATLAB". Comput. Phys. Commun. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[120] Paketet QUBIT4MATLAB är tillgängligt på https://​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433 och på den personliga hemsidan https://​/​gtoth.eu/​qubit4matlab.html.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Citerad av

[1] Laurent Lafleche, "Quantum Optimal Transport and Weak Topologies", arXiv: 2306.12944, (2023).

Ovanstående citat är från SAO / NASA ADS (senast uppdaterad framgångsrikt 2023-10-16 14:47:44). Listan kan vara ofullständig eftersom inte alla utgivare tillhandahåller lämpliga och fullständiga citatdata.

Det gick inte att hämta Crossref citerade data under senaste försöket 2023-10-16 14:47:42: Det gick inte att hämta citerade data för 10.22331 / q-2023-10-16-1143 från Crossref. Detta är normalt om DOI registrerades nyligen.

Detta papper publiceras i Quantum under Creative Commons Attribution 4.0 International (CC BY 4.0) licens. Upphovsrätten kvarstår med de ursprungliga upphovsrättsinnehavarna som författarna eller deras institutioner.

Tidsstämpel:

Mer från Quantum Journal