Kvantna Wassersteinova razdalja na podlagi optimizacije nad ločljivimi stanji

Kvantna Wassersteinova razdalja na podlagi optimizacije nad ločljivimi stanji

Časovni žig: 16. oktober 2023 10:35
Izvorno vozlišče: 2938953

Géza Tóth1,2,3,4,5 in József Pitrik5,6,7

1Teoretična fizika, Univerza v Baskiji UPV/EHU, ES-48080 Bilbao, Španija
2EHU Quantum Center, Univerza v Baskiji UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biskaja, Španija
3Donostia International Physics Center (DIPC), ES-20080 San Sebastián, Španija
4IKERBASQUE, Baskovska fundacija za znanost, ES-48011 Bilbao, Španija
5Inštitut za fiziko in optiko trdne snovi, Wignerjev raziskovalni center za fiziko, HU-1525 Budimpešta, Madžarska
6Inštitut za matematiko Alfréd Rényi, Reáltanoda u. 13-15., HU-1053 Budimpešta, Madžarska
7Oddelek za analizo in operacijske raziskave, Inštitut za matematiko, Univerza za tehnologijo in ekonomijo v Budimpešti, Müegyetem rkp. 3., HU-1111 Budimpešta, Madžarska

Se vam zdi ta članek zanimiv ali želite razpravljati? Zaslišite ali pustite komentar na SciRate.

Minimalizem

Definiramo kvantno Wassersteinovo razdaljo tako, da se optimizacija sklopitve izvaja v bipartitnih ločljivih stanjih in ne v bipartitnih kvantnih stanjih na splošno, in preučujemo njene lastnosti. Presenetljivo ugotovimo, da je samodistanca povezana s kvantno Fisherjevo informacijo. Predstavljamo transportni zemljevid, ki ustreza optimalnemu bipartitnemu ločljivemu stanju. Razpravljamo o tem, kako je uvedena kvantna Wassersteinova razdalja povezana s kriteriji za zaznavanje kvantne prepletenosti. Definiramo varianci podobne količine, ki jih lahko dobimo iz kvantne Wassersteinove razdalje z zamenjavo minimizacije nad kvantnimi stanji z maksimizacijo. Naše rezultate razširimo na družino posplošenih kvantnih Fisherjevih informacijskih količin.

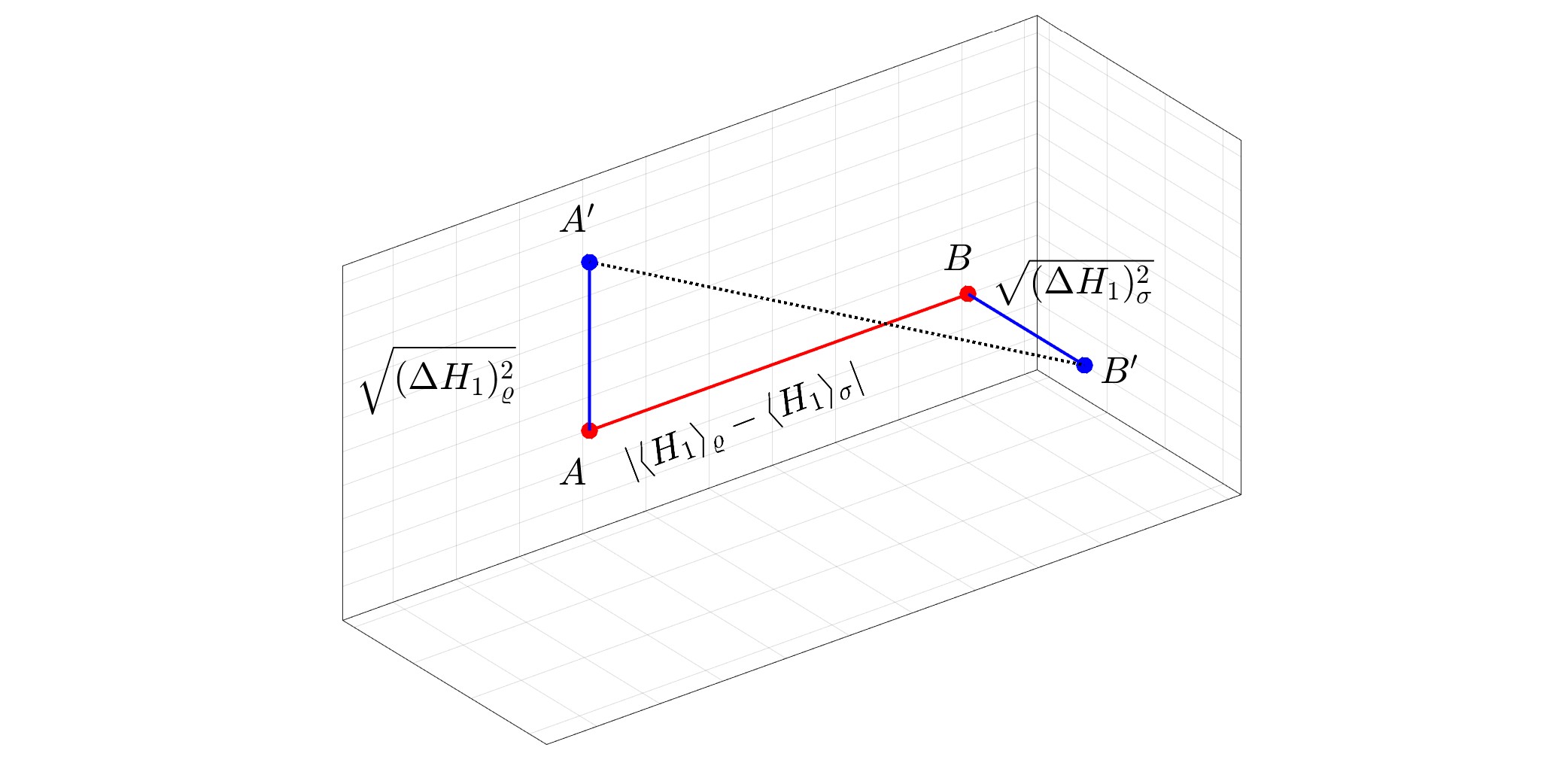
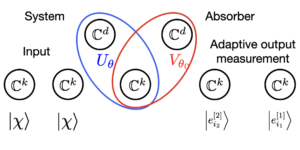
Prikazana slika: Geometrijska predstavitev kvantne Wassersteinove razdalje med čistim stanjem $varrho$ in mešanim stanjem $sigma$ za $N=1.$ Kvantna Wassersteinova razdalja je enaka $1/sqrt2$-kratniku običajne evklidske razdalje med $A'$ in $B'.$

Priljubljen povzetek

V vsakdanjem življenju nam razdalja dveh mest pove, koliko kilometrov moramo prevoziti od enega do drugega. Kako enostavno lahko pridemo iz enega mesta v drugo, je mogoče opredeliti tudi z merjenjem porabe goriva med našo potjo. Slednji je bolj informativen v smislu, da odraža stroške potovanja, povezane s topografijo ceste, tj. je občutljiv na osnovno metriko. Nato si predstavljajmo, da moramo premakniti kup peska z enega mesta na drugega in novi kup ima lahko drugačno obliko. Tudi v tem primeru lahko napor pri premikanju peska označimo s stroški transporta.

Razdalje imajo osrednjo vlogo v matematiki, fiziki in tehniki. Temeljna težava v verjetnosti in statistiki je najti uporabne mere razdalje med dvema verjetnostnima porazdelitvama. Na žalost so številni pojmi razdalje med verjetnostnimi porazdelitvami, recimo p(x) in q(x), maksimalni, če se med seboj ne prekrivajo, tj. ena je vedno enaka nič, ko je druga različna od nič. To je nepraktično za številne aplikacije. Če se na primer vrnemo k analogiji s peskom, se zdi, da sta dva kupa peska, ki se ne prekrivata, enako oddaljena drug od drugega, ne glede na to, ali je njuna razdalja 10 km ali 100 km. Optimalna transportna teorija je način za konstruiranje alternativnega pojma razdalje med verjetnostnimi porazdelitvami, tako imenovane Wassersteinove razdalje. Lahko je nemaksimalna, tudi če se distribucije med seboj ne prekrivajo, je občutljiva na osnovno metriko (tj. ceno transporta) in v bistvu izraža napor, ki ga potrebujemo, da premaknemo eno k drugi, kot bi bili peščeni griči.

Nedavno je bila opredeljena kvantna Wassersteinova razdalja, ki posplošuje klasično Wassersteinovo razdaljo. Temelji na minimizaciji stroškovne funkcije nad kvantnimi stanji bipartitnega kvantnega sistema. Ima podobno lastnost kot zgoraj omenjena v kvantnem svetu. Za ortogonalna stanja je lahko nemaksimalen, kar je uporabno na primer, ko moramo algoritem naučiti kvantne podatke.

Kot lahko pričakujemo, ima tudi kvantna Wassersteinova razdalja lastnosti, ki se zelo razlikujejo od lastnosti njene klasične dvojnice. Na primer, ko merimo oddaljenost kvantnega stanja od samega sebe, je lahko različna od nič. Čeprav je to že begajoče, je bilo tudi ugotovljeno, da je samooddaljevanje povezano z informacijami o poševnosti Wigner-Yanase, ki jih je leta 1963 uvedel Nobelov nagrajenec EP Wigner, ki ima bistven prispevek k temeljim kvantne fizike in MM Yanase.

V našem prispevku gledamo na to skrivnostno najdbo še iz druge smeri. Zgoraj omenjeno minimizacijo omejimo na tako imenovana ločljiva stanja. To so kvantna stanja, ki ne vsebujejo prepletenosti. Ugotavljamo, da samodistanca postane kvantna Fisherjeva informacija, ki je osrednja količina v kvantnem meroslovju in teoriji kvantnega ocenjevanja ter se pojavlja na primer v znameniti Cramer-Raovi meji. S preučevanjem lastnosti takšne Wassersteinove razdalje naše delo utira pot povezovanju teorije kvantne Wassersteinove razdalje s teorijo kvantne prepletenosti.

► BibTeX podatki

► Reference

[1] G. Monge. "Mémoire sur la héory des déblais et des remblais". Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L. Kantorovič. "O premeščanju množic". Management Science 5, 1–4 (1958). url: http://​/​www.jstor.org/​stable/​2626967.
http: / / www.jstor.org/ stable / 2626967

[3] Emmanuel Boissard, Thibaut Le Gouic in Jean-Michel Loubes. “Ocena distribucijske predloge z metriko wasserstein”. Bernoulli 21, 740–759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

[4] Oleg Butkovski. “Subgeometrične stopnje konvergence Markovljevih procesov v Wassersteinovi metriki”. Ann. Appl. verjetno. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[5] M. Hairer, J.-C. Mattingly in M. Scheutzow. “Asimptotična sklopitev in splošna oblika Harrisovega izreka z aplikacijami na stohastične enačbe z zakasnitvijo”. verjetno. Teorija Relat. Polja 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[6] M. Hairer in JC Mattingly. “Spektralne vrzeli v Wassersteinovih razdaljah in 2D stohastične Navier-Stokesove enačbe”. Ann. verjetno. 36, 2050–2091 (2008).
https://doi.org/ 10.1214/08-AOP392

[7] A. Figalli, F. Maggi in A. Pratelli. "Pristop množičnega prevoza k kvantitativnim izoperimetričnim neenakostim". Izumiti. matematika 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli in F. Maggi. "O obliki kapljic tekočine in kristalov v režimu majhne mase". Arh. obrok. Meh. Analno 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[9] J. Lott in C. Villani. "Riccijeva ukrivljenost za prostore z metričnimi merami prek optimalnega transporta". Ann. matematike. 169 (3), 903–991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

[10] Max-K. von Renesse in Karl-Theodor Sturm. »Transportne neenakosti, ocene gradientov, entropija in Riccijeva ukrivljenost«. Komunikacija Pure Appl. matematika 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[11] Karl-Theodor Sturm. “O geometriji metričnih merskih prostorov I”. Acta Math. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[12] Karl-Theodor Sturm. “O geometriji metričnih merskih prostorov II”. Acta Math. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[13] Benoit Kloeckner. “Geometrična študija Wassersteinovih prostorov: evklidski prostori”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03

[14] György Pál Gehér, Tamás Titkos in Dániel Virosztek. “O izometričnih vložitvah wassersteinovih prostorov – diskretni primer”. J. Math. Analno Appl. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. “Izometrična študija Wassersteinovih prostorov – realna črta”. Trans. Amer. matematika Soc. 373, 5855–5883 (2020).
https://​/​doi.org/​10.1090/​tran/​8113

[16] György Pál Gehér, Tamás Titkos in Dániel Virosztek. “Izometrična skupina Wassersteinovih prostorov: Hilbertov primer”. J. Lond. matematika Soc. 106, 3865–3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

[17] György Pál Gehér, Tamás Titkos in Dániel Virosztek. "Izometrična togost Wassersteinovih torusov in krogel". Matematika 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[18] Gergely Kiss in Tamás Titkos. “Izometrična togost wassersteinovih prostorov: primer grafične metrike”. Proc. Am. matematika Soc. 150, 4083–4097 (2022).
https://​/​doi.org/​10.1090/​proc/​15977

[19] György Pál Gehér, Tamás Titkos in Dániel Virosztek. "O eksotičnem izometričnem toku kvadratnega wassersteinovega prostora preko realne črte". Linearna algebra Appl. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, SR Park in GK Rohde. "Radonova kumulativna porazdelitvena transformacija in njena uporaba pri klasifikaciji slik". IEEE Trans. Postopek slike. 25, 920–934 (2016).
https://​/​doi.org/​10.1109/​TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek in GK Rohde. "Linearni optimalen transportni okvir za kvantifikacijo in vizualizacijo variacij v nizih slik". Int. J. Računalništvo. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. »Optimalen transport mase: aplikacije za obdelavo signalov in strojno učenje«. Revija IEEE Signal Processing Magazine 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

[23] A. Gramfort, G. Peyré in M. Cuturi. »Hitro optimalno transportno povprečenje podatkov o slikanju nevronov«. Obdelava informacij v medicinskem slikanju. IPMI 2015. Lecture Notes in Computer Science 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu in X. Gu. "Klasifikacija oblik z uporabo Wassersteinove razdalje za analizo možganske morfometrije". Obdelava informacij v medicinskem slikanju. IPMI 2015. Lecture Notes in Computer Science 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala in Léon Bottou. "Wassersteinova generativna kontradiktorna omrežja". V Doina Precup in Yee Whye Teh, urednika, Zbornik 34. mednarodne konference o strojnem učenju. Zvezek 70 Proceedings of Machine Learning Research, strani 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] TA El Moselhy in YM Marzouk. “Bayesovo sklepanje z optimalnimi zemljevidi”. J. Računalništvo. Phys. 231, 7815–7850 (2012).
https://​/​doi.org/​10.1016/​j.jcp.2012.07.022

[27] Gabriel Peyré in Marco Cuturi. »Optimalni računalniški transport: z aplikacijami v podatkovni znanosti«. Najden. Trendi strojnega učenja. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya in Tomaso A Poggio. “Učenje z izgubo wassersteina”. V C. Cortes, N. Lawrence, D. Lee, M. Sugiyama in R. Garnett, uredniki, Advances in Neural Information Processing Systems. Zvezek 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[29] A. Ramdas, NG Trillos in M. Cuturi. "O Wassersteinovem dvovzorčnem testiranju in sorodnih družinah neparametričnih testov". Entropija 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[30] S. Srivastava, C. Li in DB Dunson. "Skalabilen Bayes prek Barycentra v prostoru Wasserstein". J. Mach. Naučite se. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski in Wojeciech Slomczynski. "Mongejeva razdalja med kvantnimi stanji". J. Phys. O: Matematika. Gen. 31, 9095–9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[32] Karol Życzkowski in Wojciech Slomczynski. "Mongejeva metrika na sferi in geometriji kvantnih stanj". J. Phys. O: Matematika. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[33] Ingemar Bengtsson in Karol Życzkowski. "Geometrija kvantnih stanj: Uvod v kvantno prepletenost". Cambridge University Press. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane in D. Voiculescu. “Prosti verjetnostni analog Wassersteinove metrike na prostoru sledi stanja”. GAFA, geom. Funk. Analno 11, 1125–1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[35] Eric A. Carlen in Jan Maas. "Analog 2-Wassersteinove metrike v nekomutativni verjetnosti, pri kateri je fermionska Fokker-Planckova enačba gradientni tok za entropijo". Komun. matematika Phys. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[36] Eric A. Carlen in Jan Maas. “Gradientni tok in entropijske neenakosti za kvantne Markove polskupine s podrobnim ravnovesjem”. J. Funk. Analno 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

[37] Eric A. Carlen in Jan Maas. “Nekomutativni račun, optimalni transport in funkcionalne neenakosti v disipativnih kvantnih sistemih”. J. Stat. Phys. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

[38] Nilanjana Datta in Cambyse Rouzé. "Koncentracija kvantnih stanj iz kvantnih funkcionalnih in transportnih stroškovnih neenakosti". J. Math. Phys. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[39] Nilanjana Datta in Cambyse Rouzé. »Povezava relativne entropije, optimalnega transporta in Fisherjevih informacij: kvantna neenakost HWI«. Ann. Henri Poincaré 21, 2115–2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[40] François Golse, Clément Mouhot in Thierry Paul. "O srednjem polju in klasičnih mejah kvantne mehanike". Komun. matematika Phys. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[41] François Golse in Thierry Paul. “Schrödingerjeva enačba v srednjem polju in semiklasičnem režimu”. Arh. obrok. Meh. Analno 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[42] François Golse in Thierry Paul. "Valovni paketi in kvadratna razdalja Monge-Kantorovich v kvantni mehaniki". Comptes Rendus Math. 356, 177–197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

[43] François Golse. “Problem kvantnega $N$-telesa v srednjem polju in semiklasičnem režimu”. Phil. Trans. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse in T. Paul. “Kvantno optimalen transport je cenejši”. J. Stat. Phys. 181, 149–162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[45] Emanuele Caglioti, François Golse in Thierry Paul. "Na poti k optimalnemu transportu za kvantne gostote". arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma in Dario Trevisan. "Kvantno optimalen transport s kvantnimi kanali". Ann. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan in Seth Lloyd. "Kvantna Wassersteinova razdalja reda 1". IEEE Trans. Inf. Teorija 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole in Karol Życzkowski. “Kvantni Monge–Kantorovichev problem in transportna razdalja med matricami gostote”. Phys. Rev. Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland in Karol Życzkowski. "Kvantno optimalen transport". arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein in K. Życzkowski. “Monotonost kvantne 2-Wassersteinove razdalje”. J. Phys. O: Matematika. Teor. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos in Dániel Virosztek. "Kvantne Wassersteinove izometrije v prostoru stanja kubita". J. Math. Analno Appl. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe in Seth Lloyd. "Wassersteinova kompleksnost kvantnih vezij". arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu in Seth Lloyd. “Učenje kvantnih podatkov z razdaljo kvantnega premikača zemlje”. Quantum Sci. Technol. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[54] EP Wigner in Mutsuo M. Yanase. “Informacijske vsebine distribucij”. Proc. Natl. Akad. Sci. ZDA 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki in Karol Horodecki. "Kvantna prepletenost". Rev. Mod. Phys. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[56] Otfried Gühne in Géza Tóth. "Zaznavanje prepletenosti". Phys. Rep. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik in Marcus Huber. "Certifikacija prepletenosti od teorije do eksperimenta". Nat. Rev. Phys. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd in Lorenzo Maccone. "Kvantno izboljšane meritve: premagovanje standardne kvantne meje". Znanost 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / znanost.1104149

[59] Matteo GA Pariz. "Kvantna ocena za kvantno tehnologijo". Int. J. Quant. Inf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna in Jan Kolodynski. “Četrto poglavje – Kvantne meje v optični interferometriji”. Prog. Optika 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze in Augusto Smerzi. “Kvantna teorija ocene faze”. V GM Tino in MA Kasevich, urednika, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Course 188, Varenna). Strani 691–741. IOS Press, Amsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Géza Tóth in Dénes Petz. “Ekstremne lastnosti variance in kvantne Fisherjeve informacije”. Phys. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[63] Sixia Yu. "Kvantne Fisherjeve informacije kot konveksna streha variance". arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

[64] Géza Tóth in Florian Fröwis. “Odnosi negotovosti z varianco in kvantne Fisherjeve informacije, ki temeljijo na konveksnih dekompozicijah gostotnih matrik”. Phys. Rev. Research 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[65] Shao-Hen Chiew in Manuel Gessner. "Izboljšanje odnosov negotovosti vsote s kvantnimi Fisherjevimi informacijami". Phys. Rev. Research 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[66] CW Helstrom. “Teorija kvantnega odkrivanja in ocenjevanja”. Academic Press, New York. (1976). url: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[67] AS Holevo. “Verjetnostni in statistični vidiki kvantne teorije”. Severna Nizozemska, Amsterdam. (1982).

[68] Samuel L. Braunstein in Carlton M. Caves. “Statistična razdalja in geometrija kvantnih stanj”. Phys. Rev. Lett. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

[69] Samuel L Braunstein, Carlton M Caves in Gerard J Milburn. “Razmerja splošne negotovosti: teorija, primeri in Lorentzova invariantnost”. Ann. Phys. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[70] Dénes Petz. “Kvantna teorija informacij in kvantna statistika”. Springer, Berlin, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[71] Géza Tóth in Iagoba Apellaniz. “Kvantno meroslovje z vidika kvantne informacijske znanosti”. J. Phys. O: Matematika. Teor. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied in Philipp Treutlein. “Kvantno meroslovje z neklasičnimi stanji atomskih ansamblov”. Rev. Mod. Phys. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[73] Marco Barbieri. “Optično kvantno meroslovje”. PRX Quantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

[74] Zoltán Léka in Dénes Petz. “Nekatere razgradnje varianc matrike”. verjetno. matematika Statist. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Dénes Petz in Dániel Virosztek. “Karakterizacijski izrek za variance matrike”. Acta Sci. matematika (Szeged) 80, 681–687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

[76] Akio Fujiwara in Hiroshi Imai. "Snop vlaken nad kolektorji kvantnih kanalov in njegova uporaba v kvantni statistiki". J. Phys. O: Matematika. Teor. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[77] BM Escher, RL de Matos Filho in L. Davidovich. "Splošni okvir za ocenjevanje končne meje natančnosti v hrupnem kvantno izboljšanem meroslovju". Nat. Phys. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński in Mădălin Guţă. "Neulovljiva Heisenbergova meja v kvantno izboljšanem meroslovju". Nat. Komun. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[79] Iman Marvian. “Operacijska interpretacija kvantnih ribiških informacij v kvantni termodinamiki”. Phys. Rev. Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

[80] Reinhard F. Werner. "Kvantna stanja s korelacijami Einstein-Podolsky-Rosen, ki dopuščajo model s skritimi spremenljivkami". Phys. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss in M. Lewenstein. “Kvantne korelacije v sistemih neločljivih delcev”. Ann. Phys. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui in Nobuhiro Yonezawa. "Menjalna simetrija in večdelna prepletenost". Phys. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[83] Pavel Horodecki. “Kriterij ločljivosti in neločljiva mešana stanja s pozitivnim delnim prenosom”. Phys. Lett. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[84] Asher Peres. "Kriterij ločljivosti za matrike gostote". Phys. Rev. Lett. 77, 1413–1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki in Ryszard Horodecki. "Vezano zapletanje je mogoče aktivirati". Phys. Rev. Lett. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

[86] Géza Tóth in Tamás Vértesi. "Kvantna stanja s pozitivnim delnim prenosom so uporabna za meroslovje". Phys. Rev. Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

[87] Scott Hill in William K. Wootters. "Prepletanje para kvantnih bitov". Phys. Rev. Lett. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

[88] William K. Wootters. "Zapletenost tvorbe poljubnega stanja dveh kubitov". Phys. Rev. Lett. 80, 2245–2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal in Armin Uhlmann. "Zapletenost pomoči". quant-ph/9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: kvant-ph / 9803033

[90] John A. Smolin, Frank Verstraete in Andreas Winter. “Preplet pomoči in večpartitne državne destilacije”. Phys. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[91] Holger F. Hofmann in Shigeki Takeuchi. "Kršitev razmerij lokalne negotovosti kot znak prepletenosti". Phys. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[92] Otfried Gühne. "Karakterizacija prepletenosti prek odnosov negotovosti". Phys. Rev. Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth in Peter Adam. "Meriji zapletenosti, ki temeljijo na razmerjih lokalne negotovosti, so strogo močnejši od merila izračunljive navzkrižne norme". Phys. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza in Géza Tóth. "Neenakosti stiskanja vrtenja za poljubno vrtenje". Phys. Rev. Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

[95] AR Edmonds. "Kotni moment v kvantni mehaniki". Princeton University Press. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[96] Géza Tóth. "Detekcija zapletenosti v optičnih mrežah bozonskih atomov s skupnimi meritvami". Phys. Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne in Hans J. Briegel. "Optimalne neenakosti stiskanja vrtenja zaznajo vezano zapletanje v modelih vrtenja". Phys. Rev. Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

[98] Géza Tóth in Morgan W Mitchell. "Generacija makroskopskih singletnih stanj v atomskih skupinah". New J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[99] Géza Tóth. "Odkrivanje večdelne prepletenosti v bližini simetričnih Dickejevih stanj". J. Opt. Soc. Am. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

[100] Géza Tóth, Tobias Moroder in Otfried Gühne. "Vrednotenje ukrepov prepletenosti konveksne strehe". Phys. Rev. Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

[101] Lieven Vandenberghe in Stephen Boyd. "Poldoločeno programiranje". SIAM Review 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[102] Géza Tóth. "Večdelno prepletanje in visoko natančno meroslovje". Phys. Rev. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé in Augusto Smerzi. "Fisherjeve informacije in večdelčna prepletenost". Phys. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki in Ryszard Horodecki. “Aktiviranje skrite meroslovne uporabnosti”. Phys. Rev. Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo in Federico M. Spedalieri. "Razločevanje ločljivih in zapletenih stanj". Phys. Rev. Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo in Federico M. Spedalieri. "Popolna družina kriterijev ločljivosti". Phys. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo in Federico M. Spedalieri. "Odkrivanje večdelne prepletenosti". Phys. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[108] Harold Ollivier in Wojciech H. Zurek. "Kvantno neskladje: merilo kvantnosti korelacije". Phys. Rev. Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

[109] L. Henderson in V. Vedral. “Klasične, kvantne in totalne korelacije”. J. Phys. O: Matematika. Gen. 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) in Ujjwal Sen. »Kvantno nesoglasje in njegovi zavezniki: pregled nedavnega napredka«. Rep. Prog. Phys. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

[111] Dénes Petz. "Kovarianca in Fisherjeva informacija v kvantni mehaniki". J. Phys. O: Matematika. Gen. 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[112] Paolo Gibilisco, Fumio Hiai in Dénes Petz. “Kvantna kovarianca, kvantne Fisherjeve informacije in razmerja negotovosti”. IEEE Trans. Inf. Teorija 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[113] D. Petz in C. Ghinea. “Uvod v kvantne Fisherjeve informacije”. Zvezek 27, strani 261–281. Svetovni znanstveni. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[114] Frank Hansen. "Metrične prilagojene informacije o poševnosti". Proc. Natl. Akad. Sci. ZDA 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami in Frank Hansen. "Enoten pristop k lokalni kvantni negotovosti in interferometrični moči z metrično prilagojenimi poševnimi informacijami". Entropija 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[116] MATLAB. "9.9.0.1524771(r2020b)". MathWorks Inc. Natick, Massachusetts (2020).

[117] MOSEK ApS. »Orodjarna za optimizacijo MOSEK za priročnik MATLAB. Različica 9.0”. (2019). url: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[118] J. Löfberg. “YALMIP: Orodjarna za modeliranje in optimizacijo v MATLAB-u”. V zborniku konference CACSD. Taipei, Tajvan (2004).

[119] Géza Tóth. “QUBIT4MATLAB V3.0: programski paket za kvantno informacijsko znanost in kvantno optiko za MATLAB”. Računalništvo. Phys. Komun. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[120] Paket QUBIT4MATLAB je na voljo na https://​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433 in na osebni domači strani https:/​/​gtoth.eu/​qubit4matlab.html.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Navedel

[1] Laurent Lafleche, “Quantum Optimal Transport and Weak Topologies”, arXiv: 2306.12944, (2023).

Zgornji citati so iz SAO / NASA ADS (zadnjič posodobljeno 2023-10-16 14:47:44). Seznam je morda nepopoln, saj vsi založniki ne dajejo ustreznih in popolnih podatkov o citiranju.

Pridobitve ni bilo mogoče Crossref citirani podatki med zadnjim poskusom 2023-10-16 14:47:42: Citiranih podatkov za 10.22331 / q-2023-10-16-1143 od Crossrefa ni bilo mogoče pridobiti. To je normalno, če je bil DOI registriran pred kratkim.

Ta dokument je objavljen v Quantumu pod Priznanje avtorstva Creative Commons 4.0 International (CC BY 4.0) licenca. Avtorske pravice ostajajo pri izvirnih imetnikih avtorskih pravic, kot so avtorji ali njihove ustanove.

Časovni žig:

Več od Quantum Journal