Kontinuirana majorizacija v kvantnem faznem prostoru

Kontinuirana majorizacija v kvantnem faznem prostoru

Časovni žig: 24. maj 2023 7:39
Izvorno vozlišče: 2674950

Zacharie Van Herstraeten1,2, Michael G. Jabbour1,3,4, in Nicolas J. Cerf1

1Center za kvantne informacije in komunikacijo, École polytechnique de Bruxelles, CP 165/59, Université libre de Bruxelles, 1050 Bruselj, Belgija
2Wyant College of Optical Sciences, Univerza v Arizoni, 1630 E. University Blvd., Tucson, AZ 85721, ZDA
3DAMTP, Center za matematične znanosti, Univerza v Cambridgeu, Cambridge CB3 0WA, Združeno kraljestvo
4Oddelek za fiziko, Tehnična univerza na Danskem, 2800 Kongens Lyngby, Danska

Se vam zdi ta članek zanimiv ali želite razpravljati? Zaslišite ali pustite komentar na SciRate.

Minimalizem

We explore the role of majorization theory in quantum phase space. To this purpose, we restrict ourselves to quantum states with positive Wigner functions and show that the continuous version of majorization theory provides an elegant and very natural approach to exploring the information-theoretic properties of Wigner functions in phase space. After identifying all Gaussian pure states as equivalent in the precise sense of continuous majorization, which can be understood in light of Hudson's theorem, we conjecture a fundamental majorization relation: any positive Wigner function is majorized by the Wigner function of a Gaussian pure state (especially, the bosonic vacuum state or ground state of the harmonic oscillator). As a consequence, any Schur-concave function of the Wigner function is lower bounded by the value it takes for the vacuum state. This implies in turn that the Wigner entropy is lower bounded by its value for the vacuum state, while the converse is notably not true. Our main result is then to prove this fundamental majorization relation for a relevant subset of Wigner-positive quantum states which are mixtures of the three lowest eigenstates of the harmonic oscillator. Beyond that, the conjecture is also supported by numerical evidence. We conclude by discussing some implications of this conjecture in the context of entropic uncertainty relations in phase space.

Priljubljen povzetek

Načelo negotovosti je eden najbolj fascinantnih pojavov v kvantni fiziki. Čeprav se morda zdi naravno, da je mogoče pare merljivih količin, kot sta položaj in zagon delca, natančno predvideti hkrati, kvantna fizika to dejansko prepoveduje za nekomutirajoče opazovalce. Heisenberg in Kennard sta to natančno določila z uporabo variance katere koli merljive količine, da bi zajela njeno negotovost. Leta kasneje je bilo Heisenbergovo načelo negotovosti preoblikovano tako, da se je obrnil na entropijo kot ustrezno sredstvo za kvantificiranje negotovosti. Tu uvajamo še močnejšo informacijsko-teoretično paradigmo za razumevanje negotovosti kvantnih spremenljivk v faznem prostoru, in sicer teorijo majorizacije.

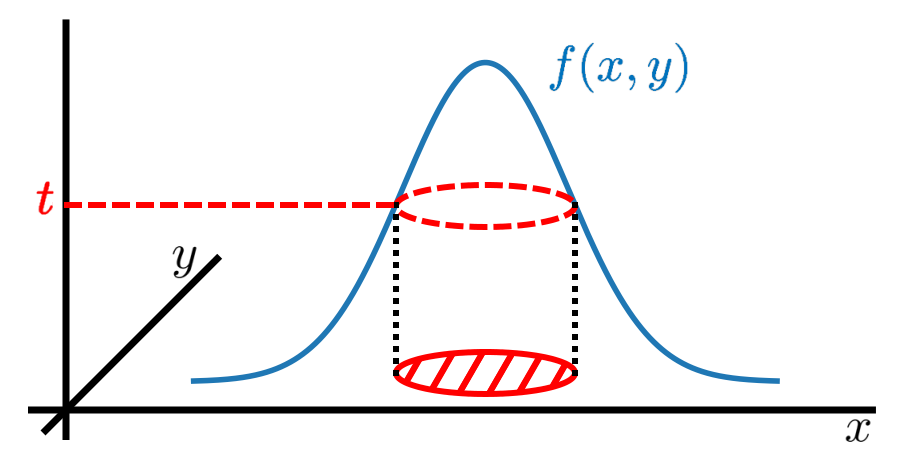
Ta matematična teorija je bila razvita pred več kot stoletjem in se uporablja na številnih področjih znanosti, od statistike do fizike. Zanimivo je, da so ga v kvantni fiziki uporabili šele relativno nedavno, kjer se je izkazalo, da je močan pristop za raziskovanje kvantne prepletenosti. Kot taka ni bila nikoli izkoriščena za karakterizacijo zveznih gostot, ki opisujejo kvantne spremenljivke v faznem prostoru, to je Wignerjevih funkcij. Kažemo, da je stalna majorizacija primerno orodje za to. Glavna usmeritev našega prispevka se nanaša na izjavo, da Wignerjeva funkcija vakuumskega stanja bozonskega načina (tj. osnovnega stanja harmoničnega oscilatorja) zvezno majorizira katero koli drugo Wignerjevo funkcijo, zaradi česar je manj negotova v smislu majorizacije. .

Čeprav izpostavljamo in razpravljamo o naših rezultatih v kontekstu kvantne optike, se ti prenašajo na kateri koli kanonični par in bi zato morali imeti posledice na različnih področjih fizike.

► BibTeX podatki

► Reference

[1] G. H. Hardy, J. E. Littlewood, and G. Pólya, ``Inequalities,''. Cambridge University Press, 1934.
https: / / doi.org/ 10.2307 / 3605504

[2] A. W. Marshall, I. Olkin, and B. C. Arnold, ``Inequalities: Theory of Majorization and its Applications,'', vol. 143. Springer, second ed., 2011.
https:/​/​doi.org/​10.1007/​978-0-387-68276-1

[3] T. Ando, ``Majorization, doubly stochastic matrices, and comparison of eigenvalues,'' Linear Algebra Appl. 118, 163–248 (1989).
https:/​/​doi.org/​10.1016/​0024-3795(89)90580-6

[4] K. Mosler, ``Majorization in economic disparity measures,'' Linear Algebra and its Applications 199, 91–114 (1994).
https:/​/​doi.org/​10.1016/​0024-3795(94)90343-3

[5] T. van Erven and P. Harremoës, ``Rényi divergence and majorization,'' in 2010 IEEE International Symposium on Information Theory, pp. 1335–1339, IEEE. 2010.
https: / / doi.org/ 10.1109 / ISIT.2010.5513784

[6] M. A. Alhejji and G. Smith, ``A Tight Uniform Continuity Bound for Equivocation,'' in 2020 IEEE International Symposium on Information Theory (ISIT), pp. 2270–2274. 2020.
https://doi.org/ 10.1109/ISIT44484.2020.9174350

[7] M. G. Jabbour and N. Datta, ``A Tight Uniform Continuity Bound for the Arimoto-Rényi Conditional Entropy and its Extension to Classical-Quantum States,'' IEEE Transactions on Information Theory 68, 2169–2181 (2022).
https: / / doi.org/ 10.1109 / TIT.2022.3142812

[8] A. Horn, ``Doubly Stochastic Matrices and the Diagonal of a Rotation Matrix,'' American Journal of Mathematics 76, 620–630 (1954).
https: / / doi.org/ 10.2307 / 2372705

[9] M. A. Nielsen, ``Conditions for a Class of Entanglement Transformations,'' Physical Review Letters 83, 436 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.83.436

[10] M. A. Nielsen and G. Vidal, ``Majorization and the interconversion of bipartite states,'' Quantum Information and Computation 1, 76–93 (2001).
https: / / doi.org/ 10.26421 / QIC1.1-5

[11] M. A. Nielsen and J. Kempe, ``Separable States Are More Disordered Globally than Locally,'' Physical Review Letters 86, 5184–5187 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.86.5184

[12] T. Hiroshima, ``Majorization Criterion for Distillability of a Bipartite Quantum State,'' Physical Review Letters 91, 057902 (2003).
https: / / doi.org/ 10.1103 / PhysRevLett.91.057902

[13] Z. Puchała, Ł. Rudnicki, and K. Życzkowski, ``Majorization entropic uncertainty relations,'' Journal of Physics A: Mathematical and Theoretical 46, 272002 (2013).
https:/​/​doi.org/​10.1088/​1751-8113/​46/​27/​272002

[14] L. Rudnicki, Z. Puchała, and K. Życzkowski, ``Strong majorization entropic uncertainty relations,'' Physical Review A 89, 052115 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.89.052115

[15] L. Rudnicki, ``Majorization approach to entropic uncertainty relations for coarse-grained observables,'' Physical Review A 91, 032123 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.91.032123

[16] F. Brandão, M. Horodecki, N. Ng, J. Oppenheim, and S. Wehner, ``The second laws of quantum thermodynamics,'' Proceedings of the National Academy of Sciences 112, 3275–3279 (2015).
https: / / doi.org/ 10.1073 / pnas.1411728112

[17] R. García-Patrón, C. Navarrete-Benlloch, S. Lloyd, J. H. Shapiro, and N. J. Cerf, ``Majorization Theory Approach to the Gaussian Channel Minimum Entropy Conjecture,'' Physical Review Letters 108, 110505 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.110505

[18] C. N. Gagatsos, O. Oreshkov, and N. J. Cerf, ``Majorization relations and entanglement generation in a beam splitter,'' Physical Review A 87, 042307 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.042307

[19] G. De Palma, D. Trevisan, and V. Giovannetti, ``Passive States Optimize the Output of Bosonic Gaussian Quantum Channels,'' IEEE Transactions on Information Theory 62, 2895–2906 (2016).
https: / / doi.org/ 10.1109 / TIT.2016.2547426

[20] M. G. Jabbour, R. García-Patrón, and N. J. Cerf, ``Majorization preservation of Gaussian bosonic channels,'' New Journal of Physics 18, 073047 (2016).
https:/​/​doi.org/​10.1088/​1367-2630/​18/​7/​073047

[21] M. G. Jabbour and N. J. Cerf, ``Fock majorization in bosonic quantum channels with a passive environment,'' Journal of Physics A: Mathematical and Theoretical 52, 105302 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​aaf0d2

[22] U. Leonhardt, ``Essential quantum optics: from quantum measurements to black holes,''. Cambridge University Press, 2010.
https: / / doi.org/ 10.1017 / CBO9780511806117

[23] A. Hertz, M. G. Jabbour, and N. J. Cerf, ``Entropy-power uncertainty relations: towards a tight inequality for all Gaussian pure states,'' Journal of Physics A: Mathematical and Theoretical 50, 385301 (2017).
https: / / doi.org/ 10.1088 / 1751-8121 / aa852f

[24] A. Hertz and N. J. Cerf, ``Continuous-variable entropic uncertainty relations,'' Journal of Physics A: Mathematical and Theoretical 52, 173001 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​ab03f3

[25] C. Weedbrook, S. Pirandola, R. García-Patrón, N. J. Cerf, T. C. Ralph, J. H. Shapiro, and S. Lloyd, ``Gaussian quantum information,'' Review of Modern Physics 84, 621–669 (2012).
https: / / doi.org/ 10.1103 / RevModPhys.84.621

[26] Z. Van Herstraeten and N. J. Cerf, ``Quantum Wigner entropy,'' Physical Review A 104, 042211 (2021).
https: / / doi.org/ 10.1103 / PhysRevA.104.042211

[27] F. J. Narcowich, ``Distributions of $hbar$-positive type and applications,'' Journal of mathematical physics 30, 2565–2573 (1989).
https: / / doi.org/ 10.1063 / 1.528537

[28] T. Bröcker and R. Werner, ``Mixed states with positive Wigner functions,'' Journal of mathematical physics 36, 62–75 (1995).
https: / / doi.org/ 10.1063 / 1.531326

[29] R. L. Hudson, ``When is the Wigner quasi-probability density non-negative?,'' Reports on Mathematical Physics 6, 249–252 (1974).
https:/​/​doi.org/​10.1016/​0034-4877(74)90007-X

[30] F. Soto in P. Claverie, "Kdaj je Wignerjeva funkcija večdimenzionalnih sistemov nenegativna?", Journal of Mathematical Physics 24, 97–100 (1983).
https: / / doi.org/ 10.1063 / 1.525607

[31] F. J. Narcowich and R. O’Connell, ``Necessary and sufficient conditions for a phase-space function to be a Wigner distribution,'' Physical Review A 34, 1 (1986).
https: / / doi.org/ 10.1103 / PhysRevA.34.1

[32] A. Mandilara, E. Karpov, and N. J. Cerf, ``Extending Hudson's theorem to mixed quantum states,'' Physical Review A 79, 062302 (2009).
https: / / doi.org/ 10.1103 / PhysRevA.79.062302

[33] A. Mandilara, E. Karpov, and N. Cerf, ``Gaussianity bounds for quantum mixed states with a positive Wigner function,'' in Journal of Physics: Conference Series, vol. 254, p. 012011, IOP Publishing. 2010.
https:/​/​doi.org/​10.1088/​1742-6596/​254/​1/​012011

[34] L. Wang and M. Madiman, ``Beyond the Entropy Power Inequality, via Rearrangements,'' IEEE Transactions on Information Theory 60, 5116–5137 (2014).
https: / / doi.org/ 10.1109 / TIT.2014.2338852

[35] G. H. Hardy, J. E. Littlewood, and G. Pólya, ``Some simple inequalities satisfied by convex functions,'' Messenger of Mathematics 58, 145–152 (1929).

[36] H. Joe, ``An ordering of dependence for distribution of k-tuples, with applications to lotto games,'' Canadian Journal of Statistics 15, 227–238 (1987).
https: / / doi.org/ 10.2307 / 3314913

[37] I. Schur, ``Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten,'' Sitzungsberichte der Berliner Mathematischen Gesellschaft 22, 416–427 (1923).

[38] A. W. Roberts and D. E. Varberg, ``Convex functions,''. Academic Press New York, 1973.
https:/​/​doi.org/​10.1016/​B978-0-444-89597-4.50013-5

[39] A. Rényi, ``On measures of entropy and information,'' in Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, vol. 4, pp. 547–562, University of California Press. 1961.

[40] Y. He, A. B. Hamza, and H. Krim, ``A generalized divergence measure for robust image registration,'' IEEE Transactions on Signal Processing 51, 1211–1220 (2003).
https://​/​doi.org/​10.1109/​TSP.2003.810305

[41] J. V. Ryff, ``Orbits of $L^1$-functions under doubly stochastic transformations,'' Transactions of the American Mathematical Society 117, 92–100 (1965).
https: / / doi.org/ 10.2307 / 1994198

[42] F. Bahrami, S. M. Manjegani, and S. Moein, ``Semi-doubly Stochastic Operators and Majorization of Integrable Functions,'' Bulletin of the Malaysian Mathematical Sciences Society 44, 693–703 (2021).
https:/​/​doi.org/​10.1007/​s40840-020-00971-2

[43] S. M. Manjegani and S. Moein, ``Majorization and semidoubly stochastic operators on $ L^{1}(X)$,'' Journal of Inequalities and Applications 2023, 1–20 (2023).
https: / / doi.org/ 10.1186 / s13660-023-02935-z

[44] I. Białynicki-Birula and J. Mycielski, ``Uncertainty relations for information entropy in wave mechanics,'' Communications in Mathematical Physics 44, 129–132 (1975).
https: / / doi.org/ 10.1007 / BF01608825

[45] A. Wehrl, ``General properties of entropy,'' Reviews of Modern Physics 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[46] E. H. Lieb, ``Proof of an entropy conjecture of Wehrl,'' in Inequalities, pp. 359–365. Springer, 2002.
https:/​/​doi.org/​10.1007/​978-3-642-55925-9_30

[47] E. H. Lieb and J. P. Solovej, ``Proof of an entropy conjecture for Bloch coherent spin states and its generalizations,'' Acta Mathematica 212, 379 (2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[48] J. R. Johansson, P. D. Nation, and F. Nori, ``QuTiP: An open-source Python framework for the dynamics of open quantum systems,'' Computer Physics Communications 183, 1760–1772 (2012).
https: / / doi.org/ 10.1016 / j.cpc.2012.02.021

[49] K. Życzkowski, P. Horodecki, A. Sanpera, and M. Lewenstein, ``Volume of the set of separable states,'' Physical Review A 58, 883 (1998).
https: / / doi.org/ 10.1103 / PhysRevA.58.883

Navedel

[1] Nuno Costa Dias and João Nuno Prata, "On a recent conjecture by Z. Van Herstraeten and N.J. Cerf for the quantum Wigner entropy", arXiv: 2303.10531, (2023).

[2] Zacharie Van Herstraeten and Nicolas J. Cerf, "Quantum Wigner entropy", Fizični pregled A 104 4, 042211 (2021).

[3] Martin Gärttner, Tobias Haas, and Johannes Noll, "Detecting continuous variable entanglement in phase space with the $Q$-distribution", arXiv: 2211.17165, (2022).

Zgornji citati so iz SAO / NASA ADS (zadnjič posodobljeno 2023-05-24 23:55:18). Seznam je morda nepopoln, saj vsi založniki ne dajejo ustreznih in popolnih podatkov o citiranju.

On Storitev, ki jo citira Crossref ni bilo najdenih podatkov o navajanju del (zadnji poskus 2023-05-24 23:55:17).

Ta dokument je objavljen v Quantumu pod Priznanje avtorstva Creative Commons 4.0 International (CC BY 4.0) licenca. Avtorske pravice ostajajo pri izvirnih imetnikih avtorskih pravic, kot so avtorji ali njihove ustanove.

Časovni žig:

Več od Quantum Journal