Vitalik Buterin prek Blog Vitalika Buterina
To je ogledalo objave na https://medium.com/@VitalikButerin/kvadratni-aritmetični-programi-od-ničle-do-junaka-f6d558cea649
V zadnjem času je bilo veliko zanimanja za tehnologijo, ki stoji za zk-SNARK, in ljudje se vedno bolj zanimajo poskuša demistificirati nekaj, kar so mnogi poimenovali »mesečeva matematika« zaradi svoje zaznane čiste nerazložljive kompleksnosti. zk-SNARK-e je res precej težko razumeti, zlasti zaradi velikega števila gibljivih delov, ki se morajo združiti, da celota deluje, a če tehnologijo razčlenimo po delih, postane razumevanje enostavnejše.
Namen te objave ni popoln uvod v zk-SNARK; predpostavlja kot osnovno znanje, da (i) veste, kaj so zk-SNARK in kaj počnejo, in (ii) poznate dovolj matematike, da lahko sklepate o stvareh, kot so polinomi (če izjava �(�)+�(�) =(�+�)(�) , kjer sta � in � polinoma, se vam zdi naravno in očitno, potem ste na pravi ravni). Namesto tega se objava poglobi v stroje, ki stojijo za tehnologijo, in poskuša čim bolje razložiti prvo polovico plinovoda, kot ga je tukaj narisal raziskovalec zk-SNARK Eran Tromer:

Tukaj lahko korake razdelimo na dve polovici. Prvič, zk-SNARK-jev ni mogoče neposredno uporabiti za noben računalniški problem; namesto tega morate problem pretvoriti v pravo »obliko«, da bo problem deloval. Obrazec se imenuje "kvadratni aritmetični program" (QAP) in preoblikovanje kode funkcije v eno od teh je samo po sebi zelo netrivialno. Skupaj s postopkom za pretvorbo kode funkcije v QAP je še en postopek, ki ga je mogoče zagnati poleg, tako da lahko, če imate vnos v kodo, ustvarite ustrezno rešitev (včasih imenovano "priča" za QAP). Po tem sledi še en dokaj zapleten postopek za ustvarjanje dejanskega "dokaza o ničelnem znanju" za to pričo in ločen postopek za preverjanje dokaza, ki vam ga posreduje nekdo drug, vendar so to podrobnosti, ki jih ta objava ne obravnava. .
Primer, ki ga bomo izbrali, je preprost: dokaz, da poznate rešitev kubične enačbe: �3+�+5=35 (namig: odgovor je 3). Ta problem je dovolj preprost, da nastali QAP ne bo tako velik, da bi bil zastrašujoč, a dovolj netrivialen, da lahko vidite, da se vključijo vsi stroji.
Zapišimo našo funkcijo na naslednji način:
def qeval(x):
y = x**3
return x + y + 5Preprost programski jezik za posebne namene, ki ga uporabljamo tukaj, podpira osnovno aritmetiko (+, −, ⋅, /), potenciranje s konstantno potenco (�7, vendar ne ��) in dodeljevanje spremenljivk, kar je dovolj zmogljivo, da ga lahko teoretično naredite kateri koli izračun v njem (dokler je število računskih korakov omejeno; zanke niso dovoljene). Upoštevajte, da modulo (%) in primerjalni operatorji (<, >, ≤, ≥) NISO podprti, saj ni učinkovitega načina za izvajanje modula ali primerjave neposredno v aritmetiki končne ciklične skupine (hvaležni bodite za to; če obstaja način Če bi naredili eno ali drugo, bi bila kriptografija eliptične krivulje pokvarjena hitreje, kot bi lahko rekli "binarno iskanje" in "kitajski izrek o ostankih").
Jezik lahko razširite na modulo in primerjave tako, da zagotovite bitne razgradnje (npr. 13=23+22+1) kot pomožne vnose, s čimer dokažete pravilnost teh razčlenitev in izvedete matematiko v binarnih vezjih; v aritmetiki končnih polj je preverjanje enakosti (==) prav tako izvedljivo in v resnici nekoliko lažje, a to sta podrobnosti, v katere se zdaj ne bomo spuščali. Jezik lahko razširimo tako, da podpira pogojnike (npr. if �<5:�=7; else: �=9), tako da jih pretvorimo v aritmetično obliko: �=7⋅(�<5)+9⋅(�≥5 ), čeprav upoštevajte, da bi bilo treba izvesti obe »poti« pogojnika, in če imate veliko ugnezdenih pogojnikov, lahko to povzroči veliko količino režijskih stroškov.
Pojdimo zdaj skozi ta postopek korak za korakom. Če želite to narediti sami za kateri koli del kode, jaz tukaj implementiral prevajalnik (samo za izobraževalne namene; še ni pripravljen za izdelavo QAP-jev za resnične zk-SNARK-je!).
Ploskanje
Prvi korak je postopek "sploščenja", kjer pretvorimo izvirno kodo, ki lahko vsebuje poljubno zapletene stavke in izraze, v zaporedje stavkov, ki so dveh oblik: �=� (kjer je � lahko spremenljivka ali število ) in �=� (��) � (kjer je �� lahko +, −, ⋅, / in � in � sta lahko spremenljivki, števili ali sami podizrazi). Vsako od teh izjav si lahko predstavljate kot nekakšna logična vrata v vezju. Rezultat postopka izravnave za zgornjo kodo je naslednji:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5Če preberete izvirno kodo in kodo tukaj, lahko dokaj enostavno vidite, da sta enakovredni.
Vrata v R1CS
Zdaj to pretvorimo v nekaj, kar se imenuje sistem omejitev ranga 1 (R1CS). R1CS je zaporedje skupin treh vektorjev (�, �, �), rešitev za R1CS pa je vektor �, kjer mora � zadostiti enačbi �.�⋅�.�−�.�=0, kjer je . predstavlja pikčasti zmnožek – preprosteje povedano, če � in � zmnožimo obe vrednosti na istih položajih in nato vzamemo vsoto teh zmnožkov, nato naredimo enako z � in � ter nato � in � , potem je tretji rezultat enak produktu prvih dveh rezultatov. Na primer, to je zadovoljen R1CS:
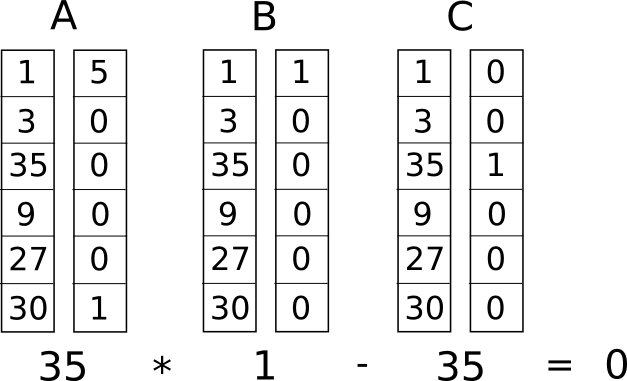
Toda namesto da bi imeli samo eno omejitev, bomo imeli veliko omejitev: eno za vsaka logična vrata. Obstaja standardni način za pretvorbo logičnih vrat v (�,�,�) trojček, odvisno od tega, kakšna je operacija (+, −, ⋅ ali /) in ali so argumenti spremenljivke ali števila. Dolžina vsakega vektorja je enaka skupnemu številu spremenljivk v sistemu, vključno z navidezno spremenljivko ~one pri prvem indeksu, ki predstavlja število 1, vhodnimi spremenljivkami, navidezno spremenljivko ~out, ki predstavlja izhod, in nato vsemi vmesne spremenljivke (���1 in ���2 zgoraj); vektorji bodo na splošno zelo redki, zapolnjevali bodo samo reže, ki ustrezajo spremenljivkam, na katere vplivajo določena logična vrata.
Najprej bomo zagotovili preslikavo spremenljivk, ki jo bomo uporabili:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'Vektor rešitve bo sestavljen iz dodelitev za vse te spremenljivke v tem vrstnem redu.
Zdaj bomo dali (�,�,�) trojček za prva vrata:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Vidite lahko, da če vektor rešitve vsebuje 3 na drugem mestu in 9 na četrtem mestu, se bo ne glede na preostalo vsebino vektorja rešitve preverjanje pikčastega produkta zmanjšalo na 3⋅3=9 in pa bo minilo. Če ima vektor rešitve −3 na drugem mestu in 9 na četrtem mestu, bo tudi preverjanje uspešno; pravzaprav, če ima vektor rešitve 7 na drugem mestu in 49 na četrtem položaju, bo to preverjanje še vedno uspešno – namen tega prvega preverjanja je preveriti konsistentnost vhodov in izhodov samo prvih vrat.
Zdaj pa pojdimo do drugih vrat:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]V podobnem slogu kot pri prvem preverjanju pikčastega produkta tukaj preverjamo, da je ���1⋅�=�.
Zdaj pa tretja vrata:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]Tukaj je vzorec nekoliko drugačen: prvi element v vektorju rešitve se pomnoži z drugim elementom, nato s petim elementom, sešteje oba rezultata in preveri, ali je vsota enaka šestemu elementu. Ker je prvi element v vektorju rešitve vedno ena, je to samo preverjanje seštevanja, s katerim se preveri, ali je izhod enak vsoti obeh vhodov.
Končno četrta vrata:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]Tukaj ocenjujemo zadnje preverjanje, ~out =���2+5. Preverjanje pikčastega zmnožka deluje tako, da vzamemo šesti element v vektorju rešitve, dodamo petkrat prvi element (opomnik: prvi element je 1, torej to dejansko pomeni dodajanje 5) in ga preverimo glede na tretji element, kjer smo shrani izhodno spremenljivko.
In tam imamo naš R1CS s štirimi omejitvami. Priča je preprosto dodelitev vsem spremenljivkam, vključno z vhodnimi, izhodnimi in notranjimi spremenljivkami:
[1, 3, 35, 9, 27, 30]To lahko izračunate sami tako, da preprosto "izvedete" zgornjo sploščeno kodo, začnete z dodelitvijo vhodne spremenljivke �=3 in vnesete vrednosti vseh vmesnih spremenljivk in izhod, ko jih izračunate.
Celoten sestavljen R1CS je:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]R1CS v QAP
Naslednji korak je ta R1CS in pretvorba v obliko QAP, ki izvaja popolnoma isto logiko, le da uporablja polinome namesto pikčastih produktov. To naredimo na naslednji način. Gremo 3od štirih skupin treh vektorjev dolžine šest do šestih skupin treh polinomov stopnje 3, kjer vrednotimo polinome pri vsakem x koordinata predstavlja eno od omejitev. To pomeni, da če ovrednotimo polinome pri �=1, potem dobimo svoj prvi niz vektorjev, če ovrednotimo polinome pri �=2, potem dobimo naš drugi niz vektorjev, in tako naprej.
To transformacijo lahko izvedemo z uporabo nečesa, kar se imenuje a Lagrangeova interpolacija. Težava, ki jo rešuje Lagrangeova interpolacija, je naslednja: če imate nabor točk (tj. (�,�) koordinatnih parov), potem z izvajanjem Lagrangeove interpolacije na teh točkah dobite polinom, ki gre skozi vse te točke. To naredimo tako, da razčlenimo problem: za vsako � koordinato ustvarimo polinom, ki ima želeno � koordinato na tej � koordinati in � koordinato 0 na vseh drugih � koordinatah, ki nas zanimajo, nato pa dobimo končno Rezultat sešteje vse polinome.
Naredimo primer. Recimo, da želimo polinom, ki poteka skozi (1,3), (2,2) in (3,4). Začnemo z izdelavo polinoma, ki gre skozi (1,3), (2,0) in (3,0). Izkazalo se je, da je izdelava polinoma, ki "štrli" pri �=1 in je nič na drugih točkah zanimanja, enostavna; preprosto naredimo:
(x - 2) * (x - 3)Kar je videti takole:
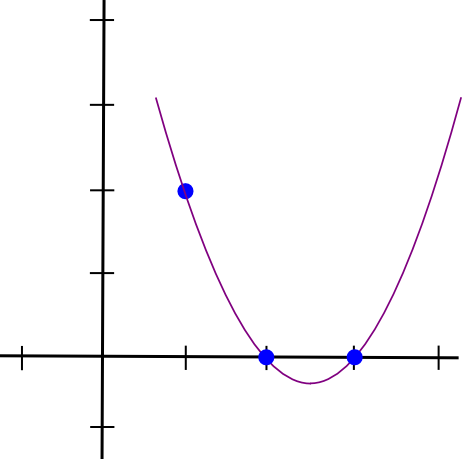
Sedaj ga moramo le še "preoblikovati", tako da bo višina pri x=1 prava:
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))Tako dobimo:
1.5 * x**2 - 7.5 * x + 9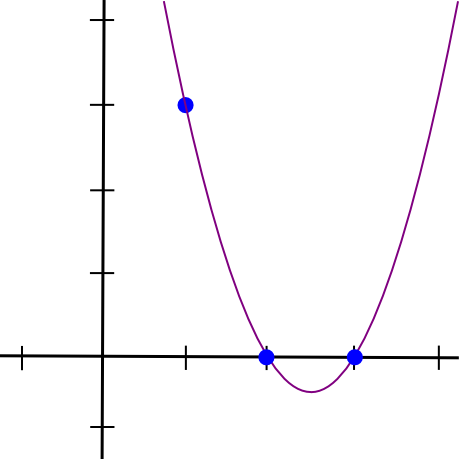
Nato naredimo enako z drugima dvema točkama in dobimo dva druga podobna polinoma, le da "štrlita" pri �=2 in �=3 namesto pri �=1. Vse tri seštejemo in dobimo:
1.5 * x**2 - 5.5 * x + 7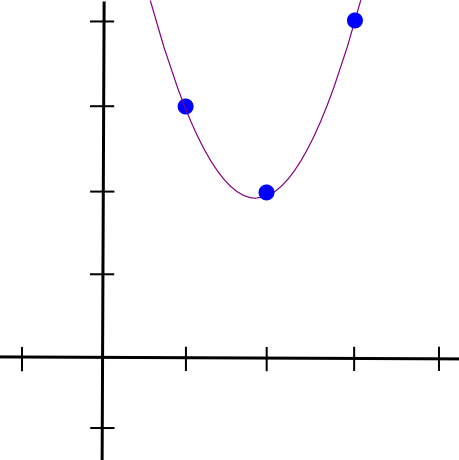
S točno takimi koordinatami, kot jih želimo. Algoritem, kot je opisan zgoraj, potrebuje �(�3) časa, saj je � točk in vsaka točka zahteva �(�2) časa za skupno množenje polinomov; z malo razmišljanja se lahko to skrajša na �(�2) čas, z veliko več razmišljanja, z uporabo hitrih Fourierjevih transformacijskih algoritmov in podobno, pa se lahko še bolj skrajša - ključna optimizacija, ko se funkcije, ki se uporabljajo v zk -SNARK-i imajo v praksi pogosto več tisoč vrat.
Zdaj pa uporabimo Lagrangeovo interpolacijo za transformacijo našega R1CS. Naredili bomo to, da bomo vzeli prvo vrednost iz vsakega vektorja �, uporabili Lagrangeovo interpolacijo, da iz tega naredimo polinom (kjer vam vrednotenje polinoma pri � pridobi prvo vrednost �-tega � vektorja), ponovimo postopek za prvo vrednost vsakega vektorja � in � in nato ta postopek ponovite za druge vrednosti, tretje vrednosti in tako naprej. Za udobje bom takoj posredoval odgovore:
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]Koeficienti so v naraščajočem vrstnem redu, tako da je prvi polinom zgoraj dejansko 0.833⋅�3—5⋅�2+9.166⋅�−5. Ta niz polinomov (in polinom Z, ki ga bom razložil kasneje) sestavlja parametre za ta določen primer QAP. Upoštevajte, da je treba vse delo do te točke opraviti samo enkrat za vsako funkcijo, ki jo poskušate preveriti z zk-SNARK-ji; Ko so parametri QAP ustvarjeni, jih je mogoče ponovno uporabiti.
Poskusimo ovrednotiti vse te polinome pri �=1. Vrednotenje polinoma pri �=1 preprosto pomeni seštevanje vseh koeficientov (kot 1�=1 za vse �), tako da ni težko. Dobimo:
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0In glej in glej, to, kar imamo tukaj, je popolnoma enako naboru treh vektorjev za prva logična vrata, ki smo jih ustvarili zgoraj.
Preverjanje QAP
Kaj je zdaj smisel te nore preobrazbe? Odgovor je, da namesto posameznega preverjanja omejitev v R1CS zdaj lahko preverimo vse omejitve hkrati s preverjanjem pikčastega produkta na polinomih.
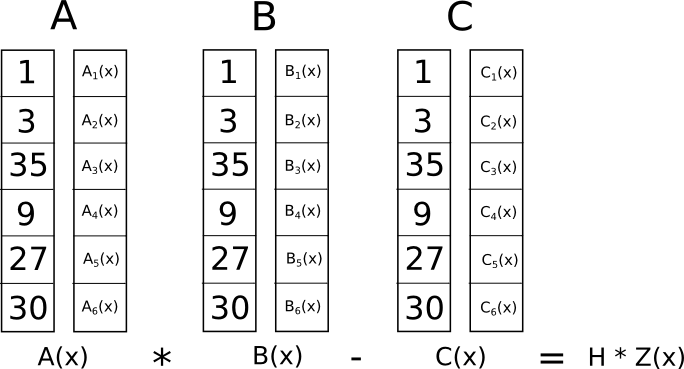
Ker je v tem primeru preverjanje pikčastega produkta serija seštevanj in množenj polinomov, bo rezultat sam polinom. Če je dobljeni polinom, ovrednoten pri vsaki koordinati �, ki smo jo uporabili zgoraj za predstavitev logičnih vrat, enak nič, potem to pomeni, da so vsa preverjanja uspešna; če nastali polinom, ovrednoten na vsaj eni od koordinat �, ki predstavljajo logična vrata, daje vrednost, ki ni ničelna, potem to pomeni, da so vrednosti, ki gredo v ta logična vrata in iz njih, nedosledne (tj. vrata so �=�⋅�� �1, vendar so podane vrednosti lahko �=2, ���1=2 in �=5).
Upoštevajte, da ni nujno, da je dobljeni polinom sam nič in v resnici v večini primerov tudi ne bo; lahko ima kakršno koli obnašanje na točkah, ki ne ustrezajo nobenim logičnim vratom, dokler je rezultat nič na vseh točkah, ki do ustrezajo nekaterim vratom. Za preverjanje pravilnosti dejansko ne ovrednotimo polinoma �=�.�⋅�.�−�.� na vsaki točki, ki ustreza vratom; namesto tega delimo � z drugim polinomom, �, in preverimo, da � enakomerno deli � – to pomeni, da deljenje �/� ne pušča ostanka.
� je definiran kot (�−1)⋅(�−2)⋅(�−3)… – najenostavnejši polinom, ki je enak nič v vseh točkah, ki ustrezajo logičnim vratom. Osnovno dejstvo algebre je, da kaj polinom, ki je enak nič na vseh teh točkah, mora biti večkratnik tega minimalnega polinoma, in če je polinom večkratnik �, potem bo njegova ocena na kateri koli od teh točk nič; ta enakovrednost nam zelo olajša delo.
Zdaj pa dejansko preverimo pikčasti produkt z zgornjimi polinomi. Najprej vmesni polinomi:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]Zdaj, �.�⋅�.�—�.�:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Zdaj pa minimalni polinom �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):
Z = [24, -50, 35, -10, 1]In če zgornji rezultat delimo z �, dobimo:
h = t / Z = [-3.666, 17.055, -3.444]Brez ostanka.
In tako imamo rešitev za QAP. Če poskušamo ponarediti katero koli od spremenljivk v rešitvi R1CS, iz katere izpeljemo to rešitev QAP – recimo, zadnjo nastavimo na 31 namesto na 30, potem dobimo polinom �, ki ne prestane enega od preverjanj (v tem posebnem primeru bi bil rezultat pri �=3 enak −1 namesto 0), poleg tega pa � ne bi bil večkratnik �; namesto tega bi deljenje �/� dalo ostanek [−5.0,8.833,−4.5,0.666].
Upoštevajte, da je zgoraj navedeno poenostavitev; »v resničnem svetu« se seštevanje, množenje, odštevanje in deljenje ne bo dogajalo z navadnimi števili, temveč z elementi končnega polja – srhljiva vrsta aritmetike, ki je samokonsistentna, torej vsi algebraični zakoni, ki jih poznamo in imamo radi, še vedno veljajo, vendar so vsi odgovori elementi neke končno velike množice, običajno cela števila v območju od 0 do �−1 za nekaj �. Na primer, če je �=13, potem je 1/2=7 (in 7⋅2=1), 3⋅5=2 in tako naprej. Uporaba aritmetike končnega polja odpravlja potrebo po skrbi za napake pri zaokroževanju in omogoča sistemu, da lepo deluje z eliptičnimi krivuljami, ki so na koncu potrebne za preostali stroj zk-SNARK, zaradi katerega je protokol zk-SNARK dejansko varen.
Posebna zahvala Eranu Tromerju za pomoč pri razlagi številnih podrobnosti o notranjem delovanju zk-SNARK-jev.
- Distribucija vsebine in PR s pomočjo SEO. Okrepite se še danes.
- PlatoData.Network Vertical Generative Ai. Opolnomočite se. Dostopite tukaj.
- PlatoAiStream. Web3 Intelligence. Razširjeno znanje. Dostopite tukaj.
- PlatoESG. Ogljik, CleanTech, Energija, Okolje, sončna energija, Ravnanje z odpadki. Dostopite tukaj.
- PlatoHealth. Obveščanje o biotehnologiji in kliničnih preskušanjih. Dostopite tukaj.
- BlockOffsets. Posodobitev okoljskega offset lastništva. Dostopite tukaj.
- vir: Platonova podatkovna inteligenca.
