1Теоретическая физика, Университет Страны Басков UPV/EHU, ES-48080 Бильбао, Испания
2Квантовый центр ЕГУ, Университет Страны Басков UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscay, Spain
3Международный физический центр Доностиа (DIPC), ES-20080 Сан-Себастьян, Испания
4IKERBASQUE, Баскский фонд науки, ES-48011 Бильбао, Испания
5Институт физики твердого тела и оптики, Исследовательский центр физики им. Вигнера, HU-1525 Будапешт, Венгрия
6Институт математики Альфреда Реньи, Realtanoda u. 13-15., HU-1053 Будапешт, Венгрия
7Кафедра анализа и исследования операций, Институт математики, Будапештский университет технологии и экономики, Müegyetem rkp. 3., HU-1111 Будапешт, Венгрия
Находите эту статью интересной или хотите обсудить? Scite или оставить комментарий на SciRate.
Абстрактные
Мы определяем квантовое расстояние Вассерштейна так, чтобы оптимизация связи осуществлялась над двучастными разделяемыми состояниями, а не над двучастными квантовыми состояниями в целом, и исследуем его свойства. Удивительно, но мы обнаружили, что внутреннее расстояние связано с квантовой информацией Фишера. Мы представляем транспортное отображение, соответствующее оптимальному двудольному разделимому состоянию. Мы обсуждаем, как введенное квантовое расстояние Вассерштейна связано с критериями обнаружения квантовой запутанности. Мы определяем величины, подобные дисперсии, которые можно получить из квантового расстояния Вассерштейна, заменяя минимизацию квантовых состояний максимизацией. Мы распространяем наши результаты на семейство обобщенных квантовых информационных величин Фишера.
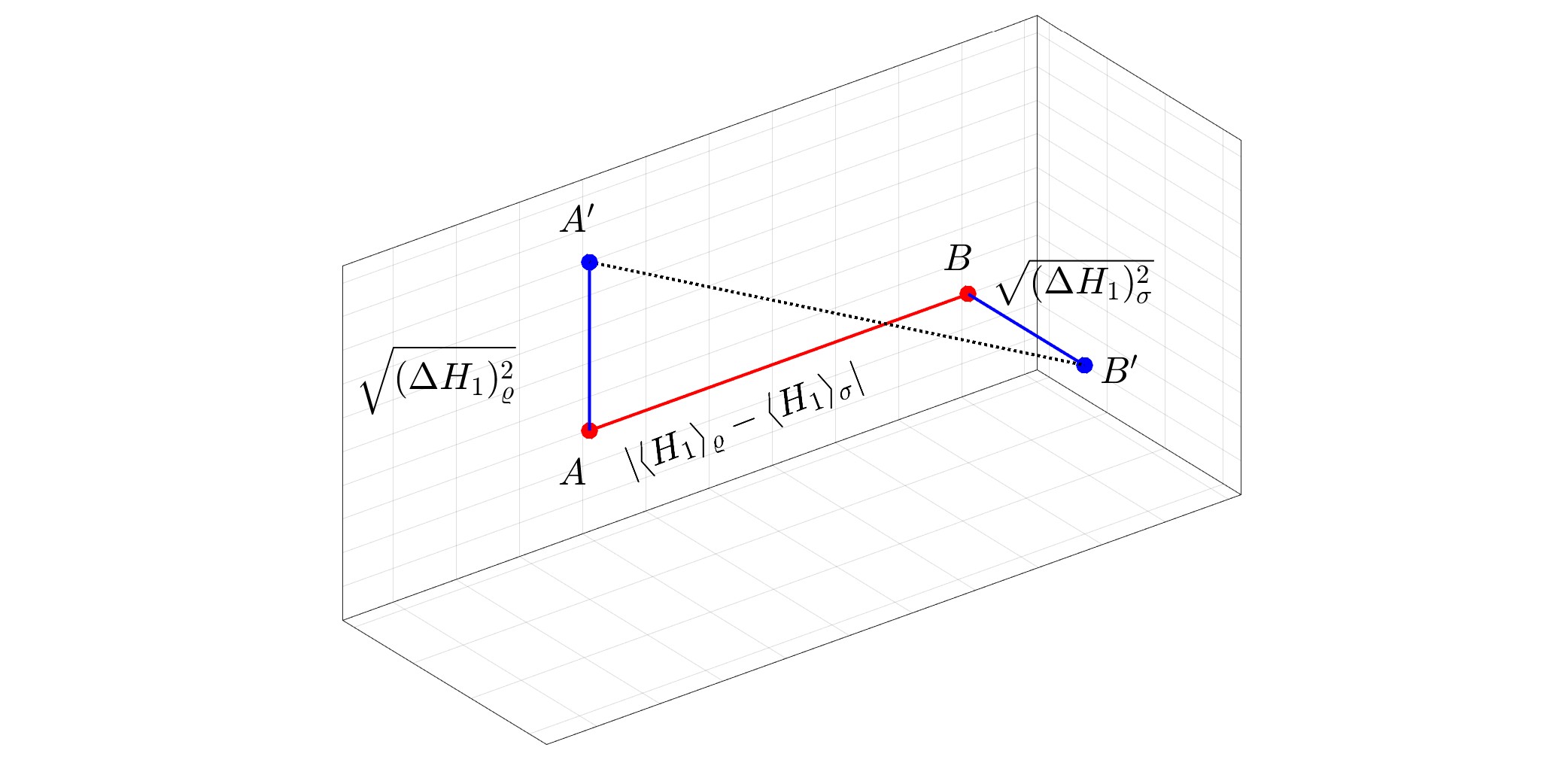
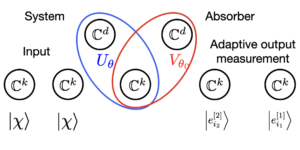
Рекомендованное изображение: Геометрическое представление квантового расстояния Вассерштейна между чистым состоянием $varrho$ и смешанным состоянием $sigma$ для $N=1.$ Квантовое расстояние Вассерштейна равно $1/sqrt2$ умноженному на обычное евклидово расстояние между $A'$ и $B'.$
Популярное резюме
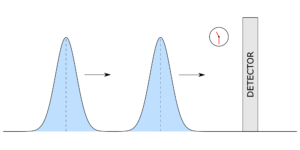
Расстояния играют центральную роль в математике, физике и технике. Фундаментальная проблема теории вероятностей и статистики — найти полезные меры расстояния между двумя распределениями вероятностей. К сожалению, многие понятия расстояния между распределениями вероятностей, скажем, p(x) и q(x), являются максимальными, если они не перекрываются друг с другом, т. е. одно всегда равно нулю, когда другое не равно нулю. Это непрактично для многих приложений. Например, возвращаясь к аналогии с песком, две непересекающиеся кучи песка кажутся одинаково далекими друг от друга, независимо от того, составляет ли их расстояние 10 км или 100 км. Теория оптимального транспорта — это способ построить альтернативное понятие расстояния между распределениями вероятностей, так называемое расстояние Вассерштейна. Оно может быть немаксимальным, даже если распределения не перекрываются друг с другом, оно чувствительно к базовому показателю (т. е. стоимости транспортировки) и, по сути, выражает усилия, необходимые для перемещения одного в другое. как будто это песчаные холмы.
Недавно было определено квантовое расстояние Вассерштейна, обобщающее классическое расстояние Вассерштейна. Он основан на минимизации функции стоимости по квантовым состояниям двудольной квантовой системы. Он обладает свойством, аналогичным упомянутому выше в квантовом мире. Оно может быть немаксимальным для ортогональных состояний, что полезно, например, когда нам нужно передать квантовые данные алгоритму.
Как мы и можем ожидать, квантовое расстояние Вассерштейна также обладает свойствами, которые сильно отличаются от свойств его классического аналога. Например, когда мы измеряем расстояние квантового состояния от самого себя, оно может быть ненулевым. Хотя это уже озадачивает, было также обнаружено, что внутреннее расстояние связано с информацией о перекосе Вигнера-Янасе, введенной в 1963 году нобелевским лауреатом Е. П. Вигнером, внесшим жизненно важный вклад в основы квантовой физики, и М. М. Янасэ.
В нашей статье мы посмотрим на эту загадочную находку с еще одной стороны. Мы ограничим упомянутую выше минимизацию так называемыми сепарабельными состояниями. Это квантовые состояния, которые не содержат запутанности. Мы обнаруживаем, что внутреннее расстояние становится квантовой информацией Фишера, величиной, центральной в квантовой метрологии и теории квантового оценивания и появляющейся, например, в знаменитой границе Крамера-Рао. Исследуя свойства такого расстояния Вассерштейна, наша работа открывает путь к соединению теории квантового расстояния Вассерштейна с теорией квантовой запутанности.
► Данные BibTeX
► Рекомендации
[1] Г. Монж. «Mémoire sur la theory des déblais et des remblais». Воспоминания о Королевской академии наук Парижа (1781 г.).
[2] Л. Канторович. «О перемещении масс». Наука управления 5, 1–4 (1958). URL: http://www.jstor.org/stable/2626967.
Http: / / www.jstor.org/ стабильный / 2626967
[3] Эммануэль Буассар, Тибо Ле Гуик и Жан-Мишель Лубес. «Шаблонная оценка распределения с метриками Вассерштейна». Бернулли 21, 740–759 (2015).
https:///doi.org/10.3150/13-bej585
[4] Олег Бутковский. «Субгеометрические скорости сходимости марковских процессов в метрике Вассерштейна». Анна. Прил. Вероятно. 24, 526–552 (2014).
https:///doi.org/10.1214/13-AAP922
[5] М. Хайрер, Ж.-К. Маттингли и М. Шутцов. «Асимптотическая связь и общая форма теоремы Харриса с приложениями к стохастическим уравнениям с запаздыванием». Вероятно. Теория Отн. Поля 149, 223–259 (2011).
https://doi.org/10.1007/s00440-009-0250-6
[6] М. Хайрер и Дж. К. Маттингли. «Спектральные щели в расстояниях Вассерштейна и двумерные стохастические уравнения Навье-Стокса». Анна. Вероятно. 2, 36–2050 (2091).
https: / / doi.org/ 10.1214 / 08-AOP392
[7] А. Фигалли, Ф. Магги и А. Прателли. «Подход массового транспорта к количественным изопериметрическим неравенствам». Изобретать. Математика. 182, 167–211. (2010).
HTTPS: / / doi.org/ 10.1007 / s00222-010-0261-г
[8] А. Фигалли и Ф. Магги. «О форме капель и кристаллов жидкости в режиме малых масс». Арх. Рацион. Мех. Анальный. 201, 143–207 (2011).
HTTPS: / / doi.org/ 10.1007 / s00205-010-0383-х
[9] Дж. Лотт и К. Виллани. «Кривизна Риччи для пространств метрической меры посредством оптимального транспорта». Анна. математики. 169 (3), 903–991 (2009).
https:///doi.org/10.48550/arXiv.math/0412127
[10] Макс-К. фон Ренессе и Карл-Теодор Штурм. «Транспортные неравенства, оценки градиента, энтропия и кривизна Риччи». Комм. Чистое приложение. Математика. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060
[11] Карл-Теодор Штурм. «К геометрии метрических пространств с мерой I». Акта Математика. 196, 65–131 (2006).
https://doi.org/10.1007/s11511-006-0002-8
[12] Карл-Теодор Штурм. «К геометрии метрических пространств с мерой II». Акта Математика. 196, 133–177 (2006).
https://doi.org/10.1007/s11511-006-0003-7
[13] Бенуа Клёкнер. «Геометрическое исследование пространств Вассерштейна: евклидовы пространства». Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03
[14] Дьёрдь Пал Гехер, Тамаш Титкос и Даниэль Вироштек. «Об изометрических вложениях пространств Вассерштейна – дискретный случай». Дж. Математика. Анальный. Прил. 480, 123435 (2019).
https:///doi.org/10.1016/j.jmaa.2019.123435
[15] Дьёрдь Пал Гехер, Т. Титкос, Даниэль Вироштек. «Изометрическое исследование пространств Вассерштейна – реальная линия». Пер. амер. Математика. Соц. 373, 5855–5883 (2020).
https: / / doi.org/ 10.1090 / tran / 8113
[16] Дьёрдь Пал Гехер, Тамаш Титкос и Даниэль Вироштек. «Группа изометрий пространств Вассерштейна: гильбертов случай». Дж. Лонд. Математика. Соц. 106, 3865–3894 (2022).
https://doi.org/10.1112/jlms.12676
[17] Дьёрдь Пал Гехер, Тамаш Титкос и Даниэль Вироштек. «Изометрическая жесткость торов и сфер Вассерштейна». Математика 69, 20–32 (2023).
https://doi.org/10.1112/mtk.12174
[18] Гергели Кисс и Тамаш Титкос. «Изометрическая жесткость пространств Вассерштейна: случай граф-метрики». Учеб. Являюсь. Математика. Соц. 150, 4083–4097 (2022).
https: / / doi.org/ 10.1090 / proc / 15977
[19] Дьёрдь Пал Гехер, Тамаш Титкос и Даниэль Вироштек. «Об экзотическом изометрическом потоке квадратичного пространства Вассерштейна над вещественной прямой». Прикладная линейная алгебра. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016
[20] С. Колоури, С.Р. Парк и Г.К. Роде. «Преобразование кумулятивного распределения радона и его применение для классификации изображений». IEEE Транс. Процесс изображения. 25, 920–934 (2016).
https: / / doi.org/ 10.1109 / TIP.2015.2509419
[21] В. Ван, Д. Слепцев, С. Басу, Дж. А. Озолек и Г. К. Роде. «Линейная оптимальная транспортная структура для количественной оценки и визуализации изменений в наборах изображений». Межд. Дж. Компьютер. Вис. 101, 254–269 (2013).
HTTPS: / / doi.org/ 10.1007 / s11263-012-0566-г
[22] С. Колоури, С. Парк, М. Торп, Д. Слепцев, Г.К. Роде. «Оптимальный массовый транспорт: приложения для обработки сигналов и машинного обучения». Журнал IEEE Signal Processing Magazine 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801
[23] А. Грамфор, Ж. Пейре и М. Кутури. «Быстрое оптимальное транспортное усреднение данных нейровизуализации». Обработка информации в медицинской визуализации. IPMI 2015. Конспекты лекций по информатике 9123, 261–272 (2015).
https://doi.org/10.1007/978-3-319-19992-4_20
[24] З. Су, В. Цзэн, Ю. Ван, З. Л. Лу и С. Гу. «Классификация форм с использованием расстояния Вассерштейна для анализа морфометрии мозга». Обработка информации в медицинской визуализации. IPMI 2015. Конспекты лекций по информатике 24, 411–423 (2015).
https://doi.org/10.1007/978-3-319-19992-4_32
[25] Мартин Арджовский, Сумит Чинтала и Леон Ботту. «Генераторно-состязательные сети Вассерштейна». Дойна Прекап и Йи Уай Тех, редакторы, Труды 34-й Международной конференции по машинному обучению. Том 70 Трудов исследований машинного обучения, страницы 214–223. ПМЛР (2017). arXiv: 1701.07875.
Arxiv: 1701.07875
[26] Т.А. Эль Моселхи и Ю.М. Марзук. «Байесовский вывод с оптимальными отображениями». Дж. Компьютер. Физ. 231, 7815–7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022
[27] Габриэль Пейре и Марко Кутури. «Вычислительная оптимальная транспортировка: с приложениями к науке о данных». Найденный. Тенденции машинного обучения. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073
[28] Чарли Фрогнер, Чиюань Чжан, Хоссейн Мобахи, Маурисио Арайя и Томазо А Поджо. «Обучение с потерей Вассерштейна». В К. Кортесе, Н. Лоуренсе, Д. Ли, М. Сугияме и Р. Гарнетте, редакторах журнала «Достижения в области нейронных систем обработки информации». Том 28. Curran Associates, Inc. (2015). arXiv: 1506.05439.
Arxiv: 1506.05439
[29] А. Рамдас, Н.Г. Триллос и М. Кутури. «О двухвыборочном тестировании Вассерштейна и связанных с ним семействах непараметрических критериев». Энтропия 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047
[30] С. Шривастава, К. Ли и Д. Б. Дансон. «Масштабируемый Байес через Барицентр в пространстве Вассерштейна». Дж. Мах. Учиться. Рез. 19, 1–35 (2018). arXiv: 1508.05880.
Arxiv: 1508.05880
[31] Кароль Жичковский и Воецех Сломчинский. «Расстояние Монжа между квантовыми состояниями». Дж. Физ. А: Математика. Быт. 31, 9095–9104 (1998).
https://doi.org/10.1088/0305-4470/31/45/009
[32] Кароль Жичковский и Войцех Сломчинский. «Метрика Монжа в сфере и геометрия квантовых состояний». Дж. Физ. А: Математика. Быт. 34, 6689–6722 (2001).
https://doi.org/10.1088/0305-4470/34/34/311
[33] Ингемар Бенгтссон и Кароль Жичковски. «Геометрия квантовых состояний: введение в квантовую запутанность». Издательство Кембриджского университета. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048
[34] П. Биане и Д. Войкулеску. «Свободно-вероятностный аналог метрики Вассерштейна в пространстве следовых состояний». ГАФА, геом. Функц. Анальный. 11, 1125–1138 (2001).
https://doi.org/10.1007/s00039-001-8226-4
[35] Эрик А. Карлен и Ян Маас. «Аналог 2-метрики Вассерштейна в некоммутативной вероятности, при которой фермионное уравнение Фоккера-Планка представляет собой градиентный поток энтропии». Коммун. Математика. Физ. 331, 887–926 (2014).
https://doi.org/10.1007/s00220-014-2124-8
[36] Эрик А. Карлен и Ян Маас. «Градиентный поток и энтропийные неравенства для квантовых марковских полугрупп с детальным балансом». Дж. Функц. Анальный. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003
[37] Эрик А. Карлен и Ян Маас. «Некоммутативное исчисление, оптимальный транспорт и функциональные неравенства в диссипативных квантовых системах». Дж. Стат. Физ. 178, 319–378 (2020).
HTTPS: / / doi.org/ 10.1007 / s10955-019-02434-ш
[38] Ниланджана Датта и Камбиз Рузе. «Концентрация квантовых состояний из квантовых функциональных неравенств и неравенств транспортных издержек». Дж. Математика. Физ. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210
[39] Ниланджана Датта и Камбиз Рузе. «Связь относительной энтропии, оптимального транспорта и информации Фишера: квантовое неравенство HWI». Анна. Анри Пуанкаре, 21 год, 2115–2150 (2020).
https://doi.org/10.1007/s00023-020-00891-8
[40] Франсуа Гольс, Клеман Муо и Тьерри Поль. «О среднем поле и классических пределах квантовой механики». Коммун. Математика. Физ. 343, 165–205 (2016).
https://doi.org/10.1007/s00220-015-2485-7
[41] Франсуа Гольс и Тьерри Поль. «Уравнение Шрёдингера в среднем поле и квазиклассическом режиме». Арх. Рацион. Мех. Анальный. 223, 57–94 (2017).
HTTPS: / / doi.org/ 10.1007 / s00205-016-1031-х
[42] Франсуа Гольс и Тьерри Поль. «Волновые пакеты и квадратичное расстояние Монжа-Канторовича в квантовой механике». Comptes Rendus Math. 356, 177–197 (2018).
https:///doi.org/10.1016/j.crma.2017.12.007
[43] Франсуа Гользе. «Квантовая задача $N$-тела в среднем поле и квазиклассическом режиме». Фил. Пер. Р. Сок. А 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229
[44] Э. Кальоти, Ф. Голс и Т. Пол. «Квантовый оптимальный транспорт дешевле». Дж. Стат. Физ. 181, 149–162 (2020).
https://doi.org/10.1007/s10955-020-02571-7
[45] Эмануэле Кальоти, Франсуа Гольс и Тьерри Поль. «На пути к оптимальному транспорту квантовых плотностей». arXiv:2101.03256 (2021).
https:///doi.org/10.48550/arXiv.2101.03256
Arxiv: 2101.03256
[46] Джакомо Де Пальма и Дарио Тревизан. «Квантовый оптимальный транспорт с квантовыми каналами». Анна. Анри Пуанкаре, 22 года, 3199–3234 (2021).
https://doi.org/10.1007/s00023-021-01042-3
[47] Джакомо Де Пальма, Милад Марвиан, Дарио Тревизан и Сет Ллойд. «Квантовое расстояние Вассерштейна первого порядка». IEEE Транс. Инф. Теория 1, 67–6627 (6643).
https: / / doi.org/ 10.1109 / TIT.2021.3076442
[48] Шмуэль Фридланд, Михал Экстайн, Сэм Коул и Кароль Жичковски. «Квантовая задача Монжа–Канторовича и транспортное расстояние между матрицами плотности». Физ. Преподобный Летт. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402
[49] Сэм Коул, Михал Экстайн, Шмуэль Фридланд и Кароль Жичковски. «Квантовый оптимальный транспорт». arXiv:2105.06922 (2021).
https:///doi.org/10.48550/arXiv.2105.06922
Arxiv: 2105.06922
[50] Р. Бистронь, М. Экстайн и К. Жичковский. «Монотонность квантового 2-вассерштейновского расстояния». Дж. Физ. А: Математика. Теор. 56, 095301 (2023).
https://doi.org/10.1088/1751-8121/acb9c8
[51] Дьёрдь Пал Гехер, Йожеф Питрик, Тамаш Титкос и Даниэль Вироштек. «Квантовые изометрии Вассерштейна в пространстве состояний кубита». Дж. Математика. Анальный. Прил. 522, 126955 (2023).
https:///doi.org/10.1016/j.jmaa.2022.126955
[52] Лу Ли, Кайфэн Бу, Дакс Эншан Ко, Артур Джаффе и Сет Ллойд. «Вассерштейновская сложность квантовых схем». arXiv: 2208.06306 (2022).
https:///doi.org/10.48550/arXiv.2208.06306
[53] Бобак Тусси Киани, Джакомо Де Пальма, Милад Марвиан, Цзы-Вэнь Лю и Сет Ллойд. «Изучение квантовых данных с расстояния квантового землетрясения». Квантовая наука. Технол. 7, 045002 (2022).
https://doi.org/10.1088/2058-9565/ac79c9
[54] Э. П. Вигнер и Муцуо М. Янасэ. «Информационное содержание раздач». Учеб. Натл. акад. наук. США 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910
[55] Рышард Городецкий, Павел Городецкий, Михал Городецкий и Кароль Городецкий. «Квантовая запутанность». Преподобный Мод. физ. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865
[56] Отфрид Гюне и Геза Тот. «Обнаружение запутанности». физ. Отчет 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004
[57] Николай Фриис, Джузеппе Витальяно, Мехул Малик и Маркус Хубер. «Сертификация запутанности от теории к эксперименту». Нац. Преподобный физ. 1, 72–87 (2019).
https://doi.org/10.1038/s42254-018-0003-5
[58] Витторио Джованнетти, Сет Ллойд и Лоренцо Макконе. «Квантовые измерения: преодоление стандартного квантового предела». Наука 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149
[59] Маттео Г.А. Париж. «Квантовая оценка квантовых технологий». Межд. Дж. Квант. Инф. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839
[60] Рафал Демкович-Добжански, Марцин Яржина и Ян Колодински. «Глава четвертая – Квантовые пределы в оптической интерферометрии». Прог. Оптика 60, 345 – 435 (2015). arXiv: 1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
Arxiv: 1405.7703
[61] Лука Пецце и Аугусто Смерзи. «Квантовая теория фазового оценивания». Г. М. Тино и М. А. Касевич, редакторы журнала «Атомная интерферометрия» (Труды Международной школы физики «Энрико Ферми», курс 188, Варенна). Страницы 691–741. IOS Press, Амстердам (2014). arXiv: 1411.5164.
Arxiv: 1411.5164
[62] Геза Тот и Денес Петц. «Экстремальные свойства дисперсии и квантовая информация Фишера». Физ. Ред. А 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324
[63] Сиксия Ю. «Квантовая информация Фишера как выпуклая крыша дисперсии». arXiv:1302.5311 (2013).
https:///doi.org/10.48550/arXiv.1302.5311
Arxiv: 1302.5311
[64] Геза Тот и Флориан Фрёвис. «Отношения неопределенности с дисперсией и квантовой информацией Фишера на основе выпуклых разложений матриц плотности». Физ. Ред. Исследования 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075
[65] Шао-Хен Чью и Мануэль Гесснер. «Улучшение отношений неопределенности суммы с помощью квантовой информации Фишера». Физ. Ред. Исследования 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076
[66] CW Хелстрем. «Квантовая теория обнаружения и оценки». Академик Пресс, Нью-Йорк. (1976). URL: www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5.
https://www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5
[67] АС Холево. «Вероятностные и статистические аспекты квантовой теории». Северная Голландия, Амстердам. (1982).
[68] Сэмюэл Л. Браунштейн и Карлтон М. Кейвс. «Статистическое расстояние и геометрия квантовых состояний». физ. Преподобный Летт. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439
[69] Сэмюэл Л. Браунштейн, Карлтон М. Кейвс и Джерард Дж. Милберн. «Обобщенные соотношения неопределенностей: теория, примеры и лоренц-инвариантность». Анна. Физ. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040
[70] Денес Петц. «Квантовая теория информации и квантовая статистика». Шпрингер, Берлин, Гейльдерберг. (2008).
https://doi.org/10.1007/978-3-540-74636-2
[71] Геза Тот и Ягоба Апелланис. «Квантовая метрология с точки зрения квантовой информатики». Дж. Физ. А: Математика. Теор. 47, 424006 (2014).
https://doi.org/10.1088/1751-8113/47/42/424006
[72] Лука Пеззе, Аугусто Смерци, Маркус К. Оберталер, Роман Шмид и Филипп Трейтлейн. «Квантовая метрология с неклассическими состояниями атомных ансамблей». Преподобный Мод. физ. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005
[73] Марко Барбьери. «Оптическая квантовая метрология». PRX Quantum 3, 010202 (2022 г.).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202
[74] Золтан Лека и Денес Петц. «Некоторые разложения матричных дисперсий». Вероятно. Математика. Статист. 33, 191–199 (2013). arXiv: 1408.2707.
Arxiv: 1408.2707
[75] Денес Петц и Даниэль Вироштек. «Теорема о характеризации матричных дисперсий». Акта Наука. Математика. (Сегед) 80, 681–687 (2014).
https://doi.org/10.14232/actasm-013-789-z
[76] Акио Фудзивара и Хироши Имаи. «Расслоение над многообразиями квантовых каналов и его применение к квантовой статистике». Дж. Физ. А: Математика. Теор. 41, 255304 (2008).
https://doi.org/10.1088/1751-8113/41/25/255304
[77] Б.М. Эшер, Р.Л. де Матос Фильо и Л. Давидович. «Общая основа для оценки предельного предела точности в шумной квантово-усовершенствованной метрологии». Нат. Физ. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958
[78] Рафал Демкович-Добжаньский, Ян Колодинский и Мэдэлин Гуцэ. «Неуловимый предел Гейзенберга в квантовой метрологии». Нат. Коммун. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067
[79] Иман Марвиан. «Оперативная интерпретация информации квантового Фишера в квантовой термодинамике». Физ. Преподобный Летт. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502
[80] Рейнхард Ф. Вернер. «Квантовые состояния с корреляциями Эйнштейна-Подольского-Розена, допускающие модель скрытой переменной». Физ. Ред. А 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277
[81] К. Эккерт, Дж. Шлиман, Д. Брюсс и М. Левенштейн. «Квантовые корреляции в системах неразличимых частиц». Анна. Физ. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268
[82] Цубаса Итикава, Тошихико Сасаки, Идзуми Цуцуи и Нобухиро Ёнезава. «Обменная симметрия и многочастная запутанность». Физ. Ред. А 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105
[83] Павел Городецкий. «Критерий разделимости и неразделимые смешанные состояния с положительной частичной транспозицией». Физ. Летт. А 232, 333–339 (1997).
https://doi.org/10.1016/S0375-9601(97)00416-7
[84] Ашер Перес. «Критерий разделимости матриц плотности». физ. Преподобный Летт. 77, 1413–1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413
[85] Павел Городецкий, Михал Городецкий и Рышард Городецкий. «Связанное запутывание можно активировать». Физ. Преподобный Летт. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056
[86] Геза Тот и Тамаш Вертези. «Квантовые состояния с положительным частичным транспонированием полезны для метрологии». Физ. Преподобный Летт. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506
[87] Скотт Хилл и Уильям К. Вуттерс. «Запутывание пары квантовых битов». Физ. Преподобный Летт. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022
[88] Уильям К. Вуттерс. «Запутанность образования произвольного состояния двух кубитов». физ. Преподобный Летт. 80, 2245–2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245
[89] Дэвид П. ДиВинченцо, Кристофер А. Фукс, Хидео Мабучи, Джон А. Смолин, Ашиш Таплиял и Армин Ульманн. «Запутывание помощи». Quant-ph/9803033 (1998).
https:///doi.org/10.48550/arXiv.quant-ph/9803033
Arxiv: колич-фот / 9803033
[90] Джон А. Смолин, Фрэнк Верстрете и Андреас Винтер. «Запутывание помощи и многосторонняя государственная дистилляция». Физ. Ред. А 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317
[91] Хольгер Ф. Хофманн и Сигэки Такеучи. «Нарушение локальных соотношений неопределенностей как признак запутанности». Физ. Ред. А 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103
[92] Отфрид Гюне. «Характеристика запутанности через отношения неопределенности». Физ. Преподобный Летт. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903
[93] Отфрид Гюне, Матьяш Мехлер, Геза Тот и Петер Адам. «Критерии запутанности, основанные на локальных соотношениях неопределенностей, строго сильнее, чем критерий вычислимой перекрестной нормы». Физ. Ред. А 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301
[94] Джузеппе Витальяно, Филипп Хиллус, Иньиго Л. Эгускиса и Геза Тот. «Спиновые сжимающие неравенства для произвольного спина». физ. Преподобный Летт. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502
[95] А. Р. Эдмондс. «Угловой момент в квантовой механике». Издательство Принстонского университета. (1957).
https: / / doi.org/ 10.1515 / 9781400884186
[96] Геза Тот. «Обнаружение запутывания в оптических решетках бозонных атомов с помощью коллективных измерений». физ. Ред. А 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327
[97] Геза Тот, Кристиан Кнапп, Отфрид Гюне и Ханс Дж. Бригель. «Оптимальные неравенства сжатия спина обнаруживают связанную запутанность в спиновых моделях». физ. Преподобный Летт. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405
[98] Геза Тот и Морган В. Митчелл. «Генерация макроскопических синглетных состояний в атомных ансамблях». Нью Дж. Физ. 12, 053007 (2010).
https://doi.org/10.1088/1367-2630/12/5/053007
[99] Геза Тот. «Обнаружение многочастичной запутанности вблизи симметричных состояний Дике». J. Опт. Соц. Являюсь. Б 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275
[100] Геза Тот, Тобиас Мородер и Отфрид Гюн. «Оценка мер по запутыванию выпуклой крыши». Физ. Преподобный Летт. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501
[101] Ливен Ванденберге и Стивен Бойд. «Полуопределенное программирование». Обзор СИАМ 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003
[102] Геза Тот. «Многочастичная запутанность и высокоточная метрология». физ. Ред. А 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322
[103] Филипп Хиллус, Веслав Ласковски, Роланд Кришек, Кристиан Швеммер, Витлеф Вечорек, Харальд Вайнфуртер, Лука Пецце и Аугусто Смерци. «Информация Фишера и многочастичная запутанность». физ. Ред. А 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321
[104] Геза Тот, Тамаш Вертези, Павел Городецкий и Рышард Городецкий. «Активация скрытой метрологической полезности». Физ. Преподобный Летт. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402
[105] AC Доэрти, Пабло А. Паррило и Федерико М. Спедальери. «Различение разделимых и запутанных состояний». Физ. Преподобный Летт. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904
[106] Эндрю К. Доэрти, Пабло А. Паррило и Федерико М. Спедальери. «Полное семейство критериев разделимости». Физ. Ред. А 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308
[107] Эндрю К. Доэрти, Пабло А. Паррило и Федерико М. Спедальери. «Обнаружение многочастной запутанности». Физ. Ред. А 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333
[108] Гарольд Оливье и Войцех Х. Зурек. «Квантовый диссонанс: мера квантовости корреляций». физ. Преподобный Летт. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901
[109] Л. Хендерсон и В. Ведрал. «Классические, квантовые и полные корреляции». Дж. Физ. А: Математика. Быт. 34, 6899 (2001).
https://doi.org/10.1088/0305-4470/34/35/315
[110] Аниндита Бера, Тамогна Дас, Дебасис Садхухан, Судипто Сингха Рой, Адити Сен (Де) и Уджвал Сен. «Квантовый диссонанс и его союзники: обзор недавнего прогресса». Реп. прог. Физ. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f
[111] Денес Петц. «Ковариация и информация Фишера в квантовой механике». Дж. Физ. А: Математика. Быт. 35, 929 (2002).
https://doi.org/10.1088/0305-4470/35/4/305
[112] Паоло Джилиско, Фумио Хиай и Денес Петц. «Квантовая ковариация, квантовая информация Фишера и соотношения неопределенностей». IEEE Транс. Инф. Теория 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142
[113] Д. Петц и К. Гинеа. «Введение в квантовую информацию Фишера». Том 27, страницы 261–281. Всемирная научная. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015
[114] Фрэнк Хансен. «Информация об асимметрии с поправкой на метрику». Учеб. Натл. акад. наук. США 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105
[115] Паоло Джилиско, Давиде Джиролами и Фрэнк Хансен. «Единый подход к локальной квантовой неопределенности и интерферометрической мощности с помощью метрической корректировки асимметричной информации». Энтропия 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263
[116] МАТЛАБ. «9.9.0.1524771(r2020b)». The MathWorks Inc. Натик, Массачусетс (2020 г.).
[117] МОСЕК АПС. «Пакет оптимизации MOSEK для руководства MATLAB. Версия 9.0». (2019). URL: docs.mosek.com/9.0/toolbox/index.html.
https:///docs.mosek.com/9.0/toolbox/index.html
[118] Й. Лёфберг. «YALMIP: набор инструментов для моделирования и оптимизации в MATLAB». В материалах конференции CACSD. Тайбэй, Тайвань (2004 г.).
[119] Геза Тот. «QUBIT4MATLAB V3.0: Пакет программ для квантовой информатики и квантовой оптики для MATLAB». Вычислить. Физ. Коммун. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007
[120] Пакет QUBIT4MATLAB доступен по адресу https://www.mathworks.com/matlabcentral/ fileexchange/8433 и на личной домашней странице https://gtoth.eu/qubit4matlab.html.
https://www.mathworks.com/matlabcentral/fileexchange/8433
Цитируется
[1] Лоран Лафлеш, «Квантовый оптимальный транспорт и слабые топологии», Arxiv: 2306.12944, (2023).
Приведенные цитаты из САО / НАСА ADS (последнее обновление успешно 2023-10-16 14:47:44). Список может быть неполным, поскольку не все издатели предоставляют подходящие и полные данные о цитировании.
Не удалось получить Перекрестная ссылка на данные во время последней попытки 2023-10-16 14:47:42: Не удалось получить цитируемые данные для 10.22331 / q-2023-10-16-1143 от Crossref. Это нормально, если DOI был зарегистрирован недавно.
Эта статья опубликована в Quantum под Creative Commons Attribution 4.0 International (CC BY 4.0) лицензия. Авторское право остается за первоначальными правообладателями, такими как авторы или их учреждения.
- SEO-контент и PR-распределение. Получите усиление сегодня.
- PlatoData.Network Вертикальный генеративный ИИ. Расширьте возможности себя. Доступ здесь.
- ПлатонАйСтрим. Интеллект Web3. Расширение знаний. Доступ здесь.
- ПлатонЭСГ. Углерод, чистые технологии, Энергия, Окружающая среда, Солнечная, Управление отходами. Доступ здесь.
- ПлатонЗдоровье. Биотехнологии и клинические исследования. Доступ здесь.
- Источник: https://quantum-journal.org/papers/q-2023-10-16-1143/
- :имеет
- :является
- :нет
- ][п
- $UP
- 003
- 07
- 1
- 10
- 100
- 102
- 107
- 11
- 110
- 116
- 118
- 12
- 125
- 13
- 14
- 15%
- 150
- 16
- 17
- 178
- 179
- 19
- 1994
- 1996
- 1998
- 1999
- 20
- 2001
- 2005
- 2006
- 2008
- 2010
- 2011
- 2012
- 2013
- 2014
- 2015
- 2016
- 2017
- 2018
- 2019
- 2020
- 2021
- 2022
- 2023
- 22
- 23
- 24
- 247
- 25
- 26
- 27
- 28
- 29
- 2D
- 30
- 31
- 32
- 33
- 35%
- 36
- 39
- 40
- 41
- 46
- 49
- 50
- 51
- 52
- 53
- 54
- 58
- 60
- 65
- 66
- 67
- 7
- 70
- 72
- 73
- 75
- 77
- 8
- 80
- 84
- 87
- 9
- 90
- 91
- 97
- 98
- a
- выше
- АБСТРАКТ НАЯ
- академический
- доступ
- активированный
- Адам
- Отрегулированный
- авансы
- состязательный
- принадлежность
- снова
- алгоритм
- Все
- уже
- причислены
- альтернатива
- всегда
- am
- Амстердам
- an
- анализ
- и
- Эндрю
- Другой
- Применение
- Приложения
- подхода
- МЫ
- Arthur
- AS
- ашер
- аспекты
- Помощь
- At
- атом
- попытка
- автор
- Авторы
- доступен
- усреднение
- b
- Баланс
- основанный
- BE
- становится
- было
- Берлин
- между
- связанный
- Мозг
- Ломать
- Будапешт
- Пакет
- by
- Кембридж
- CAN
- Может получить
- проводятся
- случаев
- Центр
- центральный
- центр
- Сертификация
- каналы
- охарактеризовать
- Чарли
- более дешевый
- Кристофер
- Город
- Город
- классификация
- собирательный
- как
- Прдч
- комментарий
- Commons
- полный
- сложность
- компьютер
- Информатика
- Конференция
- Свяжитесь
- подключенный
- строить
- потребление
- содержать
- содержание
- взносы
- Сближение
- выпуклость
- авторское право
- корреляции
- соответствующий
- Цена
- может
- контрагент
- страна
- курс
- Критерии
- Пересекать
- данным
- наука о данных
- Давид
- определять
- определенный
- задерживать
- Это
- плотность
- подробный
- обнаруживать
- обнаружение
- различный
- направление
- раздор
- обсуждать
- расстояние
- распределение
- распределения
- do
- управлять
- Капли
- в течение
- e
- Е & Т
- каждый
- земля
- легко
- Экономика
- редакторы
- усилие
- el
- Проект и
- одинаково
- Равно
- уравнения
- Эриком
- по существу
- оценка
- Оценки
- Эфир (ETH)
- Даже
- повседневный
- исследовать
- Изучение
- Примеры
- Экзотический
- ожидать
- эксперимент
- продлить
- семей
- семья
- знаменитый
- далеко
- Федерико
- поле
- Поля
- Найдите
- обнаружение
- поток
- Что касается
- форма
- образование
- найденный
- Год основания
- Устои
- 4
- Рамки
- откровенный
- Бесплатно
- от
- топливо
- функция
- функциональная
- фундаментальный
- пробелы
- Gen
- Общие
- генеративный
- генеративные состязательные сети
- геометрия
- Gerard
- получить
- график
- группы
- Гарольд
- Гарвардский
- Есть
- Скрытый
- Холмы
- держатели
- Главная
- Как
- HTML
- HTTP
- HTTPS
- i
- IEEE
- if
- ii
- изображение
- Классификация изображений
- изображений
- картина
- Изображениями
- Иман
- in
- Инк
- неравенства
- Неравенство
- информация
- информативный
- пример
- Институт
- учреждения
- интересный
- Мультиязычность
- интерпретация
- выпустили
- Введение
- iOS
- IT
- ЕГО
- саму трезвость
- Января
- JavaScript
- John
- журнал
- путешествие
- поцелуй
- Просто
- Фамилия
- Лоренс
- УЧИТЬСЯ
- изучение
- Оставлять
- чтение
- подветренный
- позволять
- li
- Лицензия
- ЖИЗНЬЮ
- ОГРАНИЧЕНИЯ
- рамки
- линия
- жидкость
- Список
- локальным
- посмотреть
- от
- машина
- обучение с помощью машины
- журнал
- управление
- руководство
- многих
- карта
- Карты
- Марко
- Маркус
- Мартин
- Масса
- Массачусетс
- массы
- математике
- математика
- матрица
- макс-ширина
- Май..
- значить
- проводить измерение
- размеры
- меры
- механика
- основным медицинским
- медицинская визуализация
- упомянутый
- метрический
- Метрика
- метрология
- может быть
- минимизация
- смешанный
- модель
- моделирование
- Модели
- Импульс
- Месяц
- БОЛЕЕ
- Морган
- двигаться
- перемещение
- таинственный
- Необходимость
- сетей
- нервный
- Новые
- New York
- следующий
- Нобелевский лауреат
- "обычные"
- Заметки
- понятие
- полученный
- окт
- of
- on
- ONE
- открытый
- Операционный отдел
- оптика
- оптимальный
- оптимизация
- or
- заказ
- оригинал
- Другое
- наши
- внешний
- за
- Пабло
- пакет
- пакеты
- страница
- страниц
- пара
- Пол
- бумага & картон
- Париж
- Парк
- Пол
- личного
- перспектива
- Питер
- фаза
- ФИЛ
- Физика
- Часть
- Платон
- Платон Интеллектуальные данные
- ПлатонДанные
- Играть
- PO
- положительный
- возможное
- мощностью
- Точность
- представить
- нажмите
- Принстон
- вероятность
- Проблема
- PROC
- Производство
- процесс
- Процессы
- обработка
- FitPartner™
- Программирование
- Прогресс
- свойства
- собственность
- обеспечивать
- опубликованный
- издатель
- Издатели
- квадратный
- квант
- количественный
- количество
- Квантовый
- квантовая запутанность
- квантовая информация
- Квантовая механика
- Квантовая оптика
- квантовая физика
- квантовые системы
- квантовая технология
- Кубит
- кубиты
- R
- Стоимость
- скорее
- реальные
- последний
- недавно
- Рекомендации
- отражает
- Несмотря на
- режим
- зарегистрированный
- Связанный
- отношения
- относительный
- остатки
- представление
- исследованиям
- ограничивать
- Итоги
- возвращение
- обзоре
- Дорога
- Роланд
- Роли
- крыша
- Рой
- Королевский
- s
- Сэм
- Сан -
- SAND
- сообщили
- Школа
- SCI
- Наука
- НАУКА
- научный
- Скотт
- казаться
- смысл
- чувствительный
- Наборы
- Форма
- Сиам
- сигнал
- подпись
- скос
- небольшой
- твердый
- Space
- пространства
- Вращение
- стандарт
- Область
- Области
- статистический
- статистика
- Стивен
- сильнее
- Кабинет
- Успешно
- такие
- подходящее
- сумма
- система
- системы
- T
- Тайвань
- Технологии
- говорит
- шаблон
- Тестирование
- тестов
- чем
- который
- Ассоциация
- График
- их
- теория
- Эти
- они
- этой
- те
- раз
- Название
- в
- Ящик для инструментов
- Всего
- транс-
- Transform
- перевозки
- трансфер
- путешествовать
- Тенденции
- два
- окончательный
- Неопределенность
- под
- лежащий в основе
- К сожалению
- унифицированный
- Университет
- обновление
- URL
- us
- через
- обычный
- изменения
- версия
- очень
- с помощью
- жизненный
- объем
- из
- W
- Ван
- хотеть
- законопроект
- Путь..
- we
- были
- когда
- будь то
- который
- в то время как
- КТО
- Уильям
- Зима
- Работа
- Мир
- X
- год
- еще
- йорк
- зефирнет
- нуль
- Чжан