Distanța cuantică Wasserstein bazată pe o optimizare asupra stărilor separabile

Distanța cuantică Wasserstein bazată pe o optimizare asupra stărilor separabile

Marca temporală: 16 octombrie 2023 10:35
Nodul sursă: 2938953

Géza Tóth1,2,3,4,5 și József Pitrik5,6,7

1Fizică teoretică, Universitatea din Țara Bascilor UPV/EHU, ES-48080 Bilbao, Spania
2EHU Quantum Center, Universitatea din Țara Bascilor UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscay, Spania
3Centrul Internațional de Fizică Donostia (DIPC), ES-20080 San Sebastián, Spania
4IKERBASQUE, Fundația Bască pentru Știință, ES-48011 Bilbao, Spania
5Institutul pentru Fizică și Optică Solid State, Centrul de Cercetare pentru Fizică Wigner, HU-1525 Budapesta, Ungaria
6Institutul de Matematică Alfred Rényi, Reáltanoda u. 13-15., HU-1053 Budapesta, Ungaria
7Departamentul de Analiză și Cercetare Operațională, Institutul de Matematică, Universitatea de Tehnologie și Economie din Budapesta, Müegyetem rkp. 3., HU-1111 Budapesta, Ungaria

Găsiți această lucrare interesant sau doriți să discutați? Scite sau lasă un comentariu la SciRate.

Abstract

Definim distanța cuantică Wasserstein astfel încât optimizarea cuplării să fie efectuată pe stări separabile bipartite, mai degrabă decât pe stările cuantice bipartite în general, și examinăm proprietățile acesteia. În mod surprinzător, aflăm că autodistanța este legată de informațiile cuantice Fisher. Prezentăm o hartă de transport corespunzătoare unei stări optime de separare bipartită. Discutăm despre modul în care distanța cuantică Wasserstein introdusă este conectată la criteriile de detectare a încurcăturii cuantice. Definim cantități asemănătoare varianței care pot fi obținute de la distanța cuantică Wasserstein prin înlocuirea minimizării stărilor cuantice cu o maximizare. Ne extindem rezultatele la o familie de cantități de informații Fisher cuantice generalizate.

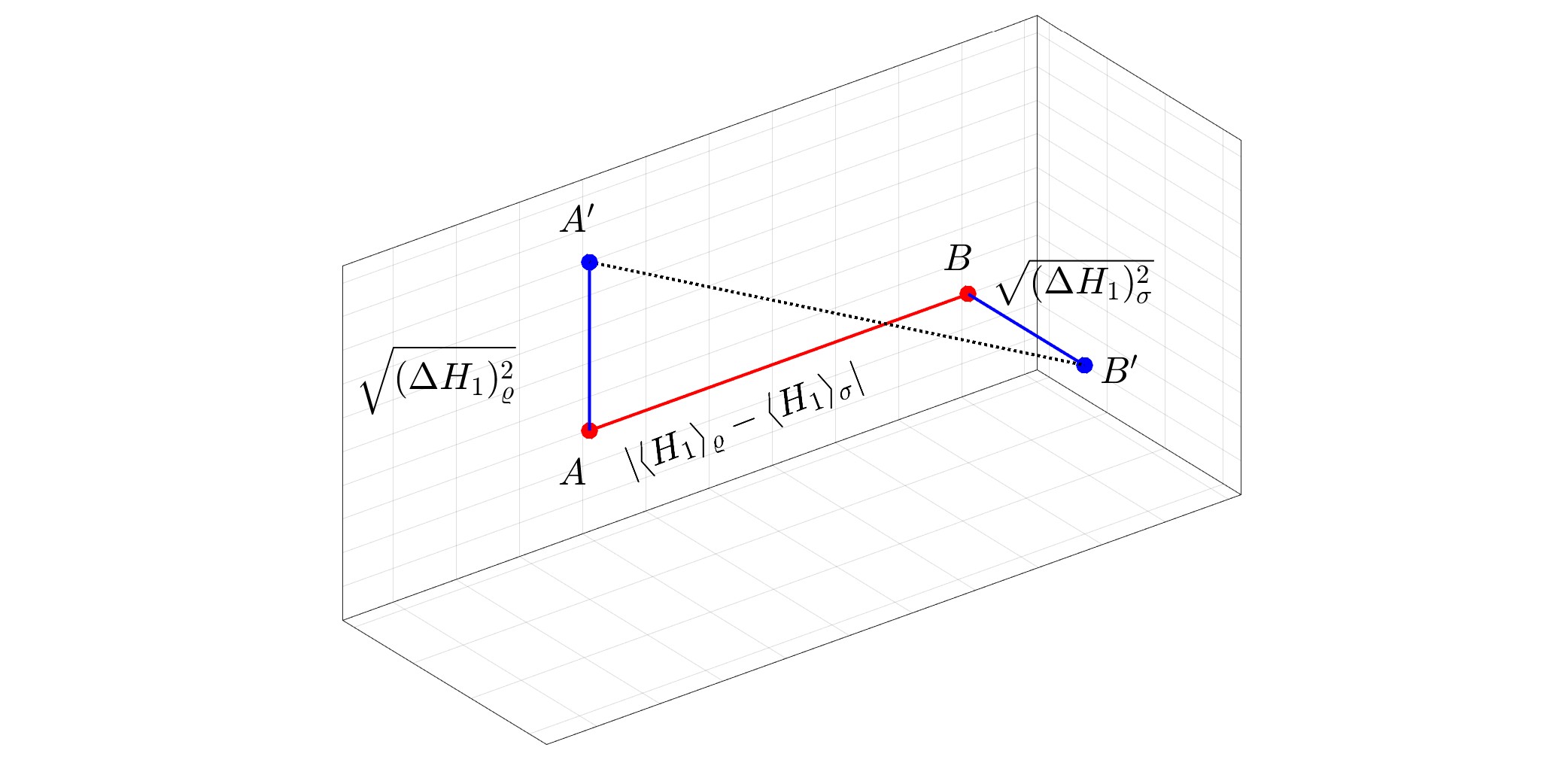
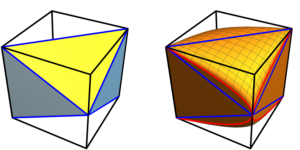
Imagine prezentată: Reprezentarea geometrică a distanței Wasserstein cuantice dintre o stare pură $varrho$ și o stare mixtă $sigma$ pentru $N=1.$ Distanța Wasserstein cuantică este egală cu $1/sqrt2$ ori distanța euclidiană obișnuită dintre $A'$ și $B'.$

Rezumat popular

În viața de zi cu zi, distanța a două orașe ne spune câți kilometri avem de parcurs de la unul la altul. De asemenea, este posibil să se caracterizeze cât de ușor putem ajunge dintr-un oraș în altul este măsurarea consumului de combustibil în timpul călătoriei noastre. Acesta din urmă este mai informativ în sensul că reflectă costul călătoriei legat de topografia drumului, adică este sensibil la metrica de bază. Apoi, să ne imaginăm că trebuie să mutăm o grămadă de nisip dintr-un loc în altul și că noul morman ar putea avea o formă diferită. În acest caz, din nou, putem caracteriza efortul de deplasare a nisipului prin costul transportului.

Distanțele joacă un rol central în matematică, fizică și inginerie. O problemă fundamentală în probabilitate și statistică este de a veni cu măsuri utile ale distanței dintre două distribuții de probabilitate. Din păcate, multe noțiuni de distanță dintre distribuțiile de probabilitate, să spunem p(x) și q(x), sunt maxime dacă nu se suprapun unele cu altele, adică, una este întotdeauna zero când cealaltă este diferită de zero. Acest lucru nu este practic pentru multe aplicații. De exemplu, revenind la analogia cu nisipul, două grămezi de nisip care nu se suprapun par să fie la fel de departe unul de celălalt, indiferent dacă distanța lor este de 10 km sau 100 km. Teoria transportului optim este o modalitate de a construi o noțiune alternativă de distanță între distribuțiile de probabilitate, așa-numita distanță Wasserstein. Poate fi non-maximal chiar dacă distribuțiile nu se suprapun între ele, este sensibil la metrica subiacentă (adică, costul transportului) și, în esență, exprimă efortul de care avem nevoie pentru a ne muta una la alta, de parcă ar fi dealuri de nisip.

Recent, distanța cuantică Wasserstein a fost definită generalizând distanța Wasserstein clasică. Se bazează pe minimizarea unei funcții de cost peste stările cuantice ale unui sistem cuantic bipartit. Are proprietatea analogă celei menționate mai sus în lumea cuantică. Poate fi non-maximal pentru stările ortogonale, ceea ce este util, de exemplu, atunci când trebuie să predăm datele cuantice unui algoritm.

După cum ne putem aștepta, distanța cuantică Wasserstein are și proprietăți foarte diferite de cele ale omologul său clasic. De exemplu, atunci când măsurăm distanța unei stări cuantice față de ea însăși, aceasta poate fi diferită de zero. Deși acest lucru este deja surprinzător, s-a constatat, de asemenea, că distanța de sine este legată de informațiile declinate Wigner-Yanase, introduse în 1963 de laureatul Nobel EP Wigner, care are contribuții vitale la bazele fizicii cuantice și MM Yanase.

În lucrarea noastră, ne uităm la această descoperire misterioasă din altă direcție. Limităm minimizarea menționată mai sus la așa-numitele stări separabile. Acestea sunt stările cuantice care nu conțin întanglement. Găsim că autodistanța devine informația cuantică Fisher, o cantitate centrală în metrologia cuantică și teoria estimării cuantice și care apare, de exemplu, în faimoasa legătură Cramer-Rao. Examinând proprietățile unei astfel de distanțe Wasserstein, munca noastră deschide calea pentru a conecta teoria distanței cuantice Wasserstein cu teoria întanglementării cuantice.

► Date BibTeX

► Referințe

[1] G. Monge. „Mémoire sur la theory des deblais et des remblais”. Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L. Kantorovici. „Despre translocarea maselor”. Management Science 5, 1–4 (1958). url: http://​/​www.jstor.org/​stable/​2626967.
http: / / www.jstor.org/ stabil / 2626967

[3] Emmanuel Boissard, Thibaut Le Gouic și Jean-Michel Loubes. „Estimarea șablonului de distribuție cu valori Wasserstein”. Bernoulli 21, 740–759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

[4] Oleg Butkovski. „Ratele subgeometrice de convergență ale proceselor Markov în metrica Wasserstein”. Ann. Aplic. Probabil. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[5] M. Hairer, J.-C. Mattingly şi M. Scheutzow. „Cuplarea asimptotică și o formă generală a teoremei lui Harris cu aplicații la ecuațiile stochastice de întârziere”. Probabil. Teoria Relat. Câmpurile 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[6] M. Hairer și JC Mattingly. „Lacunele spectrale în distanțe Wasserstein și ecuațiile stochastice 2D Navier-Stokes”. Ann. Probabil. 36, 2050–2091 (2008).
https: / / doi.org/ 10.1214 / 08-AOP392

[7] A. Figalli, F. Maggi şi A. Pratelli. „O abordare a transportului în masă a inegalităților izoperimetrice cantitative”. Inventa. Matematică. 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli şi F. Maggi. „Despre forma picăturilor lichide și a cristalelor în regimul de masă mică”. Arc. Raţie. Mech. Anal. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[9] J. Lott şi C. Villani. „Curbura Ricci pentru spații de măsurare metrică prin transport optim”. Ann. de Matematică. 169 (3), 903–991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

[10] Max-K. von Renesse și Karl-Theodor Sturm. „Inegalități de transport, estimări de gradient, entropie și curbură Ricci”. Comm. Pure Appl. Matematică. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[11] Karl-Theodor Sturm. „Despre geometria spațiilor de măsură metrice I”. Acta Math. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[12] Karl-Theodor Sturm. „Despre geometria spațiilor de măsură metrice II”. Acta Math. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[13] Benoı̂t Kloeckner. „Un studiu geometric al spațiilor Wasserstein: spații euclidiene”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03

[14] György Pál Gehér, Tamás Titkos și Dániel Virosztek. „Despre înglobările izometrice ale spațiilor Wasserstein – cazul discret”. J. Matematică. Anal. Appl. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. „Studiul izometric al spațiilor Wasserstein – linia reală”. Trans. Amer. Matematică. Soc. 373, 5855–5883 (2020).
https://​/​doi.org/​10.1090/​tran/​8113

[16] György Pál Gehér, Tamás Titkos și Dániel Virosztek. „Grupul de izometrie al spațiilor Wasserstein: cazul Hilbertian”. J. Lond. Matematică. Soc. 106, 3865–3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

[17] György Pál Gehér, Tamás Titkos și Dániel Virosztek. „Rigiditatea izometrică a torilor și sferelor Wasserstein”. Mathematika 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[18] Gergely Kiss și Tamás Titkos. „Rigiditatea izometrică a spațiilor Wasserstein: cazul metricii graficului”. Proc. A.m. Matematică. Soc. 150, 4083–4097 (2022).
https://​/​doi.org/​10.1090/​proc/​15977

[19] György Pál Gehér, Tamás Titkos și Dániel Virosztek. „Despre fluxul de izometrie exotică a spațiului Wasserstein pătratic peste linia reală”. Aplicația algebră liniară. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, SR Park și GK Rohde. „Transformarea de distribuție cumulativă a radonului și aplicarea acesteia la clasificarea imaginilor”. IEEE Trans. Procesul de imagine. 25, 920–934 (2016).
https://​/​doi.org/​10.1109/​TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek si GK Rohde. „Un cadru de transport optim liniar pentru cuantificarea și vizualizarea variațiilor în seturi de imagini”. Int. J. Comput. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. „Transport de masă optim: procesarea semnalului și aplicații de învățare automată”. IEEE Signal Processing Magazine 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

[23] A. Gramfort, G. Peyré și M. Cuturi. „Media rapidă a transportului optim al datelor de neuroimagini”. Prelucrarea informațiilor în imagistica medicală. IPMI 2015. Lecture Notes in Computer Science 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu și X. Gu. „Clasificarea formelor folosind distanța Wasserstein pentru analiza morfometriei creierului”. Prelucrarea informațiilor în imagistica medicală. IPMI 2015. Lecture Notes in Computer Science 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala și Léon Bottou. „Rețele adversare generative Wasserstein”. În Doina Precup și Yee Whye Teh, editori, Proceedings of the 34th International Conference on Machine Learning. Volumul 70 din Proceedings of Machine Learning Research, paginile 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] TA El Moselhy și YM Marzouk. „Inferența bayesiană cu hărți optime”. J. Comput. Fiz. 231, 7815–7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022

[27] Gabriel Peyré și Marco Cuturi. „Transport optim computațional: cu aplicații în știința datelor”. Găsite. Trends Machine Learn. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya și Tomaso A Poggio. „Învățarea cu o pierdere Wasserstein”. În C. Cortes, N. Lawrence, D. Lee, M. Sugiyama și R. Garnett, editori, Advances in Neural Information Processing Systems. Volumul 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[29] A. Ramdas, NG Trillos şi M. Cuturi. „Despre testarea cu două probe Wasserstein și familiile înrudite de teste neparametrice”. Entropia 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[30] S. Srivastava, C. Li și DB Dunson. „Bayes scalabil prin Barycenter în spațiul Wasserstein”. J. Mach. Învăța. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski și Wojeciech Slomczynski. „Distanța Monge dintre stările cuantice”. J. Fiz. A: Matematică. Gen. 31, 9095–9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[32] Karol Życzkowski și Wojciech Slomczynski. „Metrica Monge asupra sferei și geometriei stărilor cuantice”. J. Fiz. A: Matematică. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[33] Ingemar Bengtsson și Karol Życzkowski. „Geometria stărilor cuantice: o introducere în încrucișarea cuantică”. Cambridge University Press. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane şi D. Voiculescu. „Un analog de probabilitate liberă al metricii Wasserstein pe spațiul stării de urmă”. GAFA, Geom. Funct. Anal. 11, 1125–1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[35] Eric A. Carlen și Jan Maas. „Un analog al metricii 2-Wasserstein în probabilitatea necomutativă în baza căreia ecuația Fermionic Fokker-Planck este fluxul de gradient pentru entropie”. comun. Matematică. Fiz. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[36] Eric A. Carlen și Jan Maas. „Fluxul de gradient și inegalitățile entropiei pentru semigrupurile cuantice Markov cu echilibru detaliat”. J. Funct. Anal. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

[37] Eric A. Carlen și Jan Maas. „Calcul necomutativ, transport optim și inegalități funcționale în sistemele cuantice disipative”. J. Stat. Fiz. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

[38] Nilanjana Datta și Cambyse Rouzé. „Concentrarea stărilor cuantice din inegalitățile funcționale cuantice și ale costurilor de transport”. J. Matematică. Fiz. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[39] Nilanjana Datta și Cambyse Rouzé. „Relația entropiei relative, transportul optim și informațiile Fisher: o inegalitate cuantică HWI”. Ann. Henri Poincaré 21, 2115–2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[40] François Golse, Clément Mouhot și Thierry Paul. „Despre câmpul mediu și limitele clasice ale mecanicii cuantice”. comun. Matematică. Fiz. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[41] François Golse și Thierry Paul. „Ecuația Schrödinger în câmpul mediu și regimul semiclasic”. Arc. Raţie. Mech. Anal. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[42] François Golse și Thierry Paul. „Pachetele de unde și distanța pătratică Monge-Kantorovich în mecanica cuantică”. Comptes Rendus Math. 356, 177–197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

[43] François Golse. „Problema cuantică $N$-corp în câmpul mediu și regimul semiclasic”. Phil. Trans. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse și T. Paul. „Transportul optim cuantic este mai ieftin”. J. Stat. Fiz. 181, 149–162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[45] Emanuele Caglioti, François Golse și Thierry Paul. „Spre transportul optim pentru densitățile cuantice”. arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma și Dario Trevisan. „Transport optim cuantic cu canale cuantice”. Ann. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan și Seth Lloyd. „Distanța cuantică Wasserstein de ordinul 1”. IEEE Trans. Inf. Teoria 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole și Karol Życzkowski. „Problema Quantum Monge–Kantorovici și distanța de transport între matricele de densitate”. Fiz. Rev. Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland și Karol Życzkowski. „Transport optim cuantic”. arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein și K. Życzkowski. „Monotonitatea unei distanțe cuantice 2-Wasserstein”. J. Fiz. A: Matematică. Theor. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos și Dániel Virosztek. „Izometrii cuantice Wasserstein în spațiul stărilor qubit”. J. Matematică. Anal. Appl. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe și Seth Lloyd. „Complexitatea Wasserstein a circuitelor cuantice”. arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu și Seth Lloyd. „Învățarea datelor cuantice cu distanța motorului cuantic al pământului”. Sci. cuantică. Tehnol. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[54] EP Wigner și Mutsuo M. Yanase. „Conținutul de informații al distribuțiilor”. Proc. Natl. Acad. Sci. SUA 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki și Karol Horodecki. "Legatura cuantica". Rev. Mod. Fiz. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[56] Otfried Gühne și Géza Tóth. „Detectarea încurcăturii”. Fiz. Rep. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik și Marcus Huber. „Certificarea încrucișării de la teorie la experiment”. Nat. Rev. Fiz. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd și Lorenzo Maccone. „Măsurători îmbunătățite cuantic: depășirea limitei cuantice standard”. Science 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

[59] Matteo GA Paris. „Estimarea cuantică pentru tehnologia cuantică”. Int. J. Quant. Inf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna și Jan Kolodynski. „Capitolul patru – Limitele cuantice în interferometrie optică”. Prog. Optica 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze și Augusto Smerzi. „Teoria cuantică a estimării fazelor”. În GM Tino și MA Kasevich, editori, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Curs 188, Varenna). Paginile 691–741. IOS Press, Amsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Géza Tóth și Dénes Petz. „Proprietăți extreme ale varianței și informațiilor cuantice Fisher”. Fiz. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[63] Sixia Yu. „Informația Quantum Fisher ca acoperiș convex al variației”. arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

[64] Géza Tóth și Florian Fröwis. „Relații de incertitudine cu varianța și informațiile cuantice Fisher bazate pe descompoziții convexe ale matricelor de densitate”. Fiz. Rev. Research 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[65] Shao-Hen Chiew și Manuel Gessner. „Îmbunătățirea relațiilor de incertitudine a sumei cu informațiile cuantice Fisher”. Fiz. Rev. Research 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[66] CW Helstrom. „Teoria de detecție și estimare cuantică”. Academic Press, New York. (1976). url: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[67] AS Holevo. „Aspecte probabilistice și statistice ale teoriei cuantice”. Olanda de Nord, Amsterdam. (1982).

[68] Samuel L. Braunstein și Carlton M. Caves. „Distanța statistică și geometria stărilor cuantice”. Fiz. Rev. Lett. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

[69] Samuel L Braunstein, Carlton M Caves și Gerard J Milburn. „Relații de incertitudine generalizată: teorie, exemple și invarianța Lorentz”. Ann. Fiz. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[70] Dénes Petz. „Teoria informațiilor cuantice și statistica cuantică”. Springer, Berlin, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[71] Géza Tóth și Iagoba Apellaniz. „Metrologia cuantică din perspectiva științei informației cuantice”. J. Fiz. A: Matematică. Theor. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied și Philipp Treutlein. „Metrologie cuantică cu stări neclasice ale ansamblurilor atomice”. Rev. Mod. Fiz. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[73] Marco Barbieri. „Metrologie cuantică optică”. PRX Quantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

[74] Zoltán Léka și Dénes Petz. „Unele descompuneri ale varianțelor matricei”. Probabil. Matematică. Statist. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Dénes Petz și Dániel Virosztek. „O teoremă de caracterizare pentru variațiile matriceale”. Acta Sci. Matematică. (Szeged) 80, 681–687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

[76] Akio Fujiwara și Hiroshi Imai. „Un pachet de fibre peste mai multe canale cuantice și aplicarea lui la statistica cuantică”. J. Fiz. A: Matematică. Theor. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[77] BM Escher, RL de Matos Filho și L. Davidovich. „Cadru general pentru estimarea limitei de precizie finală în metrologia cuantică zgomotoasă”. Nat. Fiz. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński și Mădălin Guţă. „Limita evazivă Heisenberg în metrologia cuantică îmbunătățită”. Nat. comun. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[79] Iman Marvian. „Interpretarea operațională a informațiilor cuantice Fisher în termodinamica cuantică”. Fiz. Rev. Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

[80] Reinhard F. Werner. „Stări cuantice cu corelații Einstein-Podolsky-Rosen care admit un model cu variabile ascunse”. Fiz. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss și M. Lewenstein. „Corelații cuantice în sistemele de particule indistinse”. Ann. Fiz. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui și Nobuhiro Yonezawa. „Simetria schimbului și încurcarea multipartită”. Fiz. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[83] Pawel Horodecki. „Criteriu de separabilitate și stări mixte inseparabile cu transpunere parțială pozitivă”. Fiz. Lett. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[84] Asher Peres. „Criteriul de separabilitate pentru matricele de densitate”. Fiz. Rev. Lett. 77, 1413–1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki și Ryszard Horodecki. „Încrucișarea legată poate fi activată”. Fiz. Rev. Lett. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

[86] Géza Tóth și Tamás Vértesi. „Starile cuantice cu transpunere parțială pozitivă sunt utile pentru metrologie”. Fiz. Rev. Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

[87] Scott Hill și William K. Wootters. „Încrucișarea unei perechi de biți cuantici”. Fiz. Rev. Lett. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

[88] William K. Wootters. „Împlicarea formării unei stări arbitrare de doi qubiți”. Fiz. Rev. Lett. 80, 2245–2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal și Armin Uhlmann. „Împlicarea asistenței”. quant-ph/​9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: Quant-ph / 9803033

[90] John A. Smolin, Frank Verstraete și Andreas Winter. „Implicarea asistenței și distilare de stat multipartită”. Fiz. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[91] Holger F. Hofmann și Shigeki Takeuchi. „Încălcarea relațiilor locale de incertitudine ca semnătură a încurcăturii”. Fiz. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[92] Otfried Gühne. „Caracterizarea încurcăturii prin relații de incertitudine”. Fiz. Rev. Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth și Peter Adam. „Criteriile de încrucișare bazate pe relațiile locale de incertitudine sunt strict mai puternice decât criteriul de normă încrucișată calculabilă”. Fiz. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza și Géza Tóth. „Spin stoarce inegalități pentru rotire arbitrară”. Fiz. Rev. Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

[95] AR Edmonds. „Momentul unghiular în mecanica cuantică”. Princeton University Press. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[96] Géza Tóth. „Detecția încurcăturii în rețelele optice ale atomilor bosonici cu măsurători colective”. Fiz. Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne și Hans J. Briegel. „Inegalitățile optime de stoarcere a spinului detectează încurcarea legată în modelele de spin”. Fiz. Rev. Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

[98] Géza Tóth și Morgan W Mitchell. „Generarea stărilor singlet macroscopice în ansambluri atomice”. New J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[99] Géza Tóth. „Detectarea încurcăturii multipartite în vecinătatea stărilor Dicke simetrice”. J. Opt. Soc. A.m. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

[100] Géza Tóth, Tobias Moroder și Otfried Gühne. „Evaluarea măsurilor de încurcare a acoperișului convex”. Fiz. Rev. Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

[101] Lieven Vandenberghe și Stephen Boyd. „Programare semidefinită”. SIAM Review 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[102] Géza Tóth. „Împlicare multipartită și metrologie de înaltă precizie”. Fiz. Rev. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé și Augusto Smerzi. „Informații Fisher și încurcarea cu mai multe particule”. Fiz. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki și Ryszard Horodecki. „Activarea utilității metrologice ascunse”. Fiz. Rev. Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo și Federico M. Spedalieri. „Distingerea stărilor separabile și încurcate”. Fiz. Rev. Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo și Federico M. Spedalieri. „Familie completă de criterii de separabilitate”. Fiz. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo și Federico M. Spedalieri. „Detectarea încurcăturii multipartite”. Fiz. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[108] Harold Ollivier și Wojciech H. Zurek. „Discordia cuantică: o măsură a cuantumului corelațiilor”. Fiz. Rev. Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

[109] L. Henderson şi V. Vedral. „Corelații clasice, cuantice și totale”. J. Fiz. A: Matematică. Gen. 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) și Ujjwal Sen. „Discord cuantic și aliații săi: o revizuire a progresului recent”. Rep. Prog. Fiz. 81, 024001 (2017).
https://​/​doi.org/​10.1088/​1361-6633/​aa872f

[111] Dénes Petz. „Covarianța și informațiile Fisher în mecanica cuantică”. J. Fiz. A: Matematică. Gen. 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[112] Paolo Gibilisco, Fumio Hiai și Dénes Petz. „Covarianța cuantică, informațiile Fisher cuantice și relațiile de incertitudine”. IEEE Trans. Inf. Teoria 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[113] D. Petz şi C. Ghinea. „Introducere în informațiile cuantice Fisher”. Volumul 27, paginile 261–281. științific mondial. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[114] Frank Hansen. „Informații de deformare ajustate metric”. Proc. Natl. Acad. Sci. SUA 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami și Frank Hansen. „O abordare unificată a incertitudinii cuantice locale și a puterii interferometrice prin informații de deformare ajustate metric”. Entropia 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[116] MATLAB. „9.9.0.1524771(r2020b)”. MathWorks Inc. Natick, Massachusetts (2020).

[117] MOSEK ApS. „Setul de instrumente de optimizare MOSEK pentru manualul MATLAB. Versiunea 9.0”. (2019). url: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[118] J. Löfberg. „YALMIP: O cutie de instrumente pentru modelare și optimizare în MATLAB”. În Proceedings of the CACSD Conference. Taipei, Taiwan (2004).

[119] Géza Tóth. „QUBIT4MATLAB V3.0: Un pachet de programe pentru știința informației cuantice și optica cuantică pentru MATLAB”. Calculator. Fiz. comun. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[120] Pachetul QUBIT4MATLAB este disponibil la https:/​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433 și pe pagina personală de pornire https:/​/​gtoth.eu/​qubit4matlab.html.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Citat de

[1] Laurent Lafleche, „Transport optim cuantic și topologii slabe”, arXiv: 2306.12944, (2023).

Citatele de mai sus sunt din ADS SAO / NASA (ultima actualizare cu succes 2023-10-16 14:47:44). Lista poate fi incompletă, deoarece nu toți editorii furnizează date de citare adecvate și complete.

Nu a putut să aducă Date citate încrucișate în ultima încercare 2023-10-16 14:47:42: Nu s-au putut prelua date citate pentru 10.22331 / q-2023-10-16-1143 de la Crossref. Acest lucru este normal dacă DOI a fost înregistrat recent.

Acest Lucru este publicat în Quantum sub Creative Commons Atribuire 4.0 internațională (CC BY 4.0) licență. Drepturile de autor rămân la deținătorii de drepturi de autor originale, precum autorii sau instituțiile lor.

Timestamp-ul:

Mai mult de la Jurnalul cuantic