Distância quântica de Wasserstein baseada em uma otimização sobre estados separáveis

Distância quântica de Wasserstein baseada em uma otimização sobre estados separáveis

Carimbo de data / hora: 16 de outubro de 2023 10h35
Nó Fonte: 2938953

Géza Tóth1,2,3,4,5 e József Pitrik5,6,7

1Física Teórica, Universidade do País Basco UPV/EHU, ES-48080 Bilbao, Espanha
2EHU Quantum Center, Universidade do País Basco UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscaia, Espanha
3Centro Internacional de Física de Donostia (DIPC), ES-20080 San Sebastián, Espanha
4IKERBASQUE, Fundação Basca para a Ciência, ES-48011 Bilbao, Espanha
5Instituto de Física e Óptica do Estado Sólido, Wigner Research Center for Physics, HU-1525 Budapeste, Hungria
6Instituto de Matemática Alfréd Rényi, Reáltanoda u. 13-15., HU-1053 Budapeste, Hungria
7Departamento de Análise e Pesquisa Operacional, Instituto de Matemática, Universidade de Tecnologia e Economia de Budapeste, Müegyetem rkp. 3., HU-1111 Budapeste, Hungria

Acha este artigo interessante ou deseja discutir? Scite ou deixe um comentário no SciRate.

Sumário

Definimos a distância quântica de Wasserstein de modo que a otimização do acoplamento seja realizada em estados separáveis ​​bipartidos, em vez de estados quânticos bipartidos em geral, e examinamos suas propriedades. Surpreendentemente, descobrimos que a autodistância está relacionada com a informação quântica de Fisher. Apresentamos um mapa de transporte correspondente a um estado separável bipartido ideal. Discutimos como a distância quântica de Wasserstein introduzida está conectada aos critérios de detecção de emaranhamento quântico. Definimos quantidades semelhantes à variância que podem ser obtidas a partir da distância quântica de Wasserstein, substituindo a minimização dos estados quânticos por uma maximização. Estendemos nossos resultados a uma família de quantidades de informação quânticas generalizadas de Fisher.

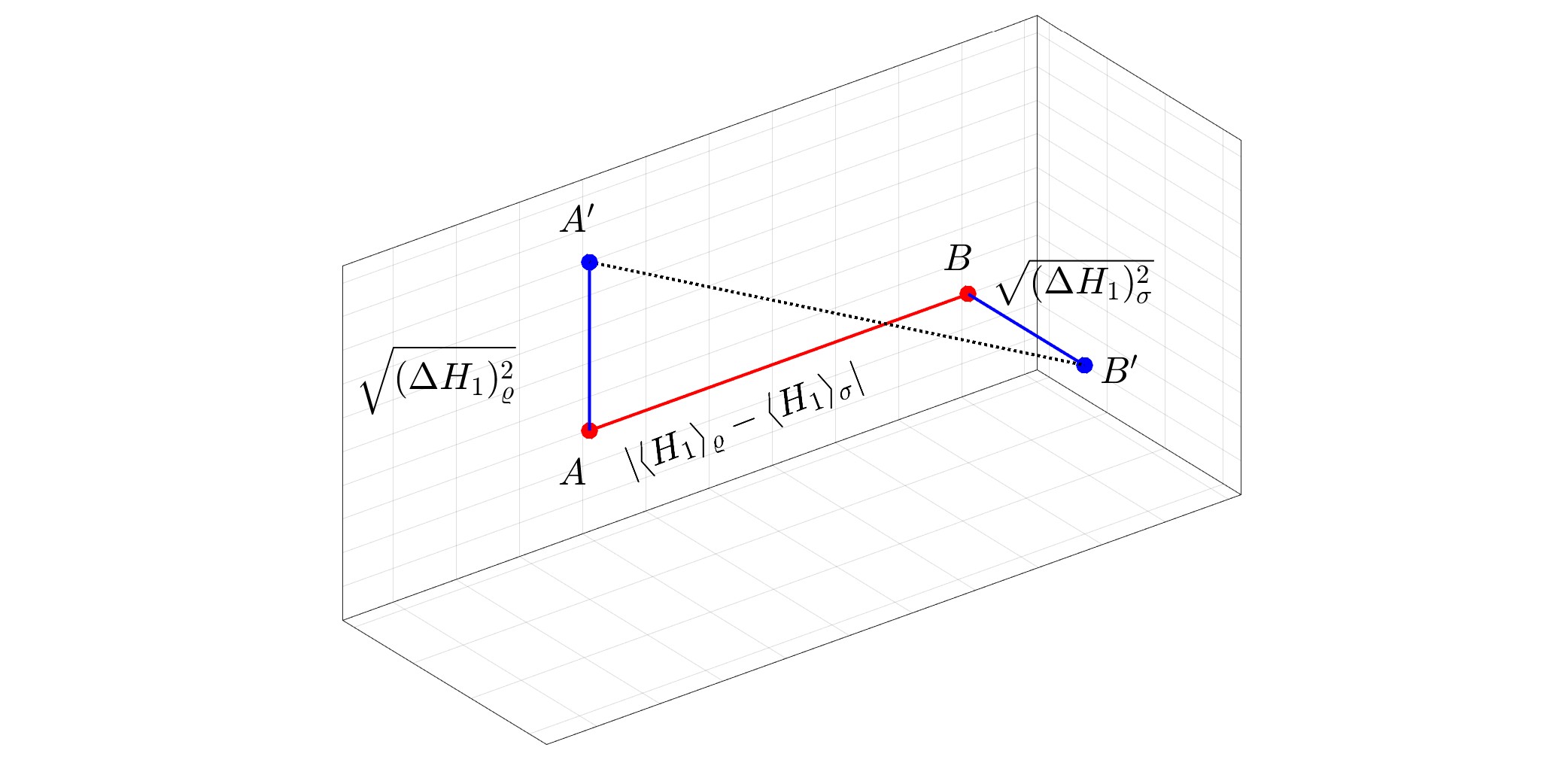
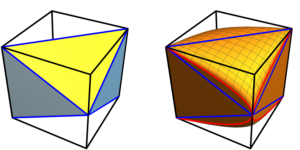
Imagem em destaque: Representação geométrica da distância quântica de Wasserstein entre um estado puro $varrho$ e um estado misto $sigma$ para $N=1.$ A distância quântica de Wasserstein é igual a $1/sqrt2$ vezes a distância euclidiana usual entre $A'$ e $B'.$

Resumo popular

Na vida quotidiana, a distância de duas cidades diz-nos quantos quilómetros temos que percorrer de uma para a outra. Também é possível caracterizar a facilidade com que podemos ir de uma cidade a outra medindo o consumo de combustível durante nosso trajeto. Este último é mais informativo no sentido de que reflecte o custo da viagem relacionado com a topografia da estrada, ou seja, o custo da viagem. ou seja, é sensível à métrica subjacente. A seguir, imaginemos que precisamos mover um monte de areia de um lugar para outro e que o novo monte possa ter uma forma diferente. Neste caso, novamente, podemos caracterizar o esforço de movimentação da areia pelo custo do transporte.

As distâncias desempenham um papel central na matemática, física e engenharia. Um problema fundamental em probabilidade e estatística é encontrar medidas úteis de distância entre duas distribuições de probabilidade. Infelizmente, muitas noções de distância entre distribuições de probabilidade, digamos p(x) e q(x), são máximas se não se sobrepuserem, ou seja. e., um é sempre zero quando o outro é diferente de zero. Isto é impraticável para muitas aplicações. Por exemplo, voltando à analogia da areia, dois montes de areia não sobrepostos parecem estar igualmente distantes um do outro, independentemente de a distância ser de 10 km ou de 100 km. A teoria do transporte ótimo é uma forma de construir uma noção alternativa de distância entre distribuições de probabilidade, a chamada distância de Wasserstein. Pode ser não máximo mesmo que as distribuições não se sobreponham, é sensível à métrica subjacente (ou seja, o custo do transporte) e, essencialmente, expressa o esforço que precisamos para mover uma para a outra, como se fossem colinas de areia.

Recentemente, a distância quântica de Wasserstein foi definida generalizando a distância clássica de Wasserstein. Baseia-se na minimização de uma função de custo sobre os estados quânticos de um sistema quântico bipartido. Possui propriedade análoga à mencionada acima no mundo quântico. Pode ser não máximo para estados ortogonais, o que é útil, por exemplo, quando precisamos ensinar dados quânticos a um algoritmo.

Como podemos esperar, a distância quântica de Wasserstein também possui propriedades muito diferentes daquelas de sua contraparte clássica. Por exemplo, quando medimos a distância de um estado quântico a si mesmo, ela pode ser diferente de zero. Embora isto já seja intrigante, também se descobriu que a auto-distância está relacionada com a informação de distorção Wigner-Yanase, introduzida em 1963 pelo Prémio Nobel E. P. Wigner, que tem contribuições vitais para os fundamentos da física quântica e M. M. Yanase.

No nosso artigo, olhamos para esta descoberta misteriosa ainda de outra direção. Restringimos a minimização mencionada acima aos chamados estados separáveis. Estes são os estados quânticos que não contêm emaranhamento. Descobrimos que a autodistância se torna a informação quântica de Fisher, uma quantidade central na metrologia quântica e na teoria da estimativa quântica, e aparecendo, por exemplo, no famoso limite de Cramer-Rao. Ao examinar as propriedades dessa distância de Wasserstein, nosso trabalho abre caminho para conectar a teoria da distância quântica de Wasserstein à teoria do emaranhamento quântico.

► dados BibTeX

► Referências

[1] G. Monge. “Mémoire sur la théory des déblais et des remblais”. Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L. Kantorovich. “Sobre a translocação de massas”. Ciência de Gestão 5, 1–4 (1958). url: http://www.jstor.org/​stable/​2626967.
http: // www.jstor.org/ stable / 2626967

[3] Emmanuel Boissard, Thibaut Le Gouic e Jean-Michel Loubes. “Modelo de estimativa de distribuição com métricas wasserstein”. Bernoulli 21, 740–759 (2015).
https:///​doi.org/​10.3150/​13-bej585

[4] Oleg Butkovsky. “Taxas subgeométricas de convergência de processos de Markov na métrica de Wasserstein”. Ana. Apl. Provavelmente. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[5] M. Hairer, J.‑C. Mattingly e M. Scheutzow. “Acoplamento assintótico e uma forma geral do teorema de Harris com aplicações a equações de atraso estocásticas”. Provavelmente. Teoria Relat. Campos 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[6] M. Hairer e JC Mattingly. “Lacunas espectrais nas distâncias de Wasserstein e nas equações estocásticas 2D de Navier-Stokes”. Ana. Provavelmente. 36, 2050–2091 (2008).
https://​/​doi.org/​10.1214/​08-AOP392

[7] A. Figalli, F. Maggi e A. Pratelli. “Uma abordagem de transporte de massa para desigualdades isoperimétricas quantitativas”. Inventar. Matemática. 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli e F. Maggi. “Sobre a forma de gotas líquidas e cristais no regime de pequena massa”. Arco. Ração. Mecânico. Anal. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[9] J. Lott e C. Villani. “Curvatura de Ricci para espaços de medidas métricas via transporte ideal”. Ana. de Matemática. 169 (3), 903–991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

[10] Max-K. von Renesse e Karl-Theodor Sturm. “Desigualdades de transporte, estimativas de gradiente, entropia e curvatura de Ricci”. Com. Aplicação Pura. Matemática. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[11] Karl-Theodor Sturm. “Sobre a geometria dos espaços de medidas métricas I”. Acta Matemática. 196, 65–131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[12] Karl-Theodor Sturm. “Sobre a geometria dos espaços de medidas métricas II”. Acta Matemática. 196, 133–177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[13] Benoı̂t Kloeckner. “Um estudo geométrico dos espaços de Wasserstein: espaços euclidianos”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03

[14] György Pál Gehér, Tamás Titkos e Dániel Virosztek. “Sobre incorporações isométricas de espaços wasserstein – o caso discreto”. J. Matemática. Anal. Apl. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. “Estudo isométrico dos espaços de Wasserstein – a linha real”. Trad. Amer. Matemática. Soc. 373, 5855–5883 (2020).
https: / / doi.org/ 10.1090 / tran / 8113

[16] György Pál Gehér, Tamás Titkos e Dániel Virosztek. “O grupo isométrico dos espaços de Wasserstein: o caso Hilbertiano”. J. Lond. Matemática. Soc. 106, 3865–3894 (2022).
https:///​doi.org/​10.1112/​jlms.12676

[17] György Pál Gehér, Tamás Titkos e Dániel Virosztek. “Rigidez isométrica de toros e esferas de Wasserstein”. Matemática 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[18] Gergely Kiss e Tamás Titkos. “Rigidez isométrica de espaços wasserstein: O caso da métrica gráfica”. Processo. Sou. Matemática. Soc. 150, 4083–4097 (2022).
https:///​doi.org/​10.1090/​proc/​15977

[19] György Pál Gehér, Tamás Titkos e Dániel Virosztek. “Sobre o fluxo isométrico exótico do espaço quadrático de Wasserstein sobre a linha real”. Aplicação de Álgebra Linear. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, SR Park e GK Rohde. “A transformação da distribuição cumulativa do Radon e sua aplicação à classificação de imagens”. IEEE Trans. Processo de imagem. 25, 920–934 (2016).
https://​/​doi.org/​10.1109/​TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, J. A. Ozolek e G. K. Rohde. “Uma estrutura de transporte linear ideal para quantificar e visualizar variações em conjuntos de imagens”. Interno. J. Computação. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. “Transporte de massa ideal: processamento de sinais e aplicações de aprendizado de máquina”. Revista IEEE Signal Processing 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

[23] A. Gramfort, G. Peyré e M. Cuturi. “Média rápida de transporte ideal de dados de neuroimagem”. Processamento de informações em imagens médicas. IPMI 2015. Notas de aula em Ciência da Computação 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, ZL Lu e X. Gu. “Classificação de formas usando distância de Wasserstein para análise de morfometria cerebral”. Processamento de informações em imagens médicas. IPMI 2015. Notas de aula em Ciência da Computação 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala e Léon Bottou. “Redes adversárias geradoras de Wasserstein”. Em Doina Precup e Yee Whye Teh, editores, Anais da 34ª Conferência Internacional sobre Aprendizado de Máquina. Volume 70 de Proceedings of Machine Learning Research, páginas 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] TA El Moselhy e YM Marzouk. “Inferência bayesiana com mapas ótimos”. J. Computação. Física. 231, 7815–7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022

[27] Gabriel Peyré e Marco Cuturi. “Transporte Computacional Ótimo: Com Aplicações à Ciência de Dados”. Encontrado. Aprendizagem automática de tendências. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya e Tomaso A Poggio. “Aprendendo com uma perda de wasserstein”. Em C. Cortes, N. Lawrence, D. Lee, M. Sugiyama e R. Garnett, editores, Advances in Neural Information Processing Systems. Volume 28. Curran Associates, Inc. arXiv:2015.
arXiv: 1506.05439

[29] A. Ramdas, NG Trillos e M. Cuturi. “Sobre testes de duas amostras de Wasserstein e famílias relacionadas de testes não paramétricos”. Entropia 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[30] S. Srivastava, C. Li e DB Dunson. “Bayes escalável via Baricentro no Espaço Wasserstein”. J. Mach. Aprender. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski e Wojeciech Slomczynski. “A distância de Monge entre estados quânticos”. J. Física. R: Matemática. Gênesis 31, 9095–9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[32] Karol Życzkowski e Wojciech Slomczynski. “A métrica Monge na esfera e geometria dos estados quânticos”. J. Física. R: Matemática. Gênesis 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[33] Ingemar Bengtsson e Karol Życzkowski. “Geometria dos estados quânticos: Uma introdução ao emaranhamento quântico”. Cambridge University Press. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane e D. Voiculescu. “Um análogo de probabilidade livre da métrica de Wasserstein no espaço de estados de rastreamento”. GAFA, Geom. Função. Anal. 11, 1125–1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[35] Eric A. Carlen e Jan Maas. “Um análogo da métrica 2-Wasserstein em probabilidade não comutativa sob a qual a equação fermiônica de Fokker-Planck é fluxo gradiente para a entropia”. Comum. Matemática. Física. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[36] Eric A. Carlen e Jan Maas. “Desigualdades de fluxo gradiente e entropia para semigrupos quânticos de Markov com equilíbrio detalhado”. J. Função. Anal. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

[37] Eric A. Carlen e Jan Maas. “Cálculo não comutativo, transporte ótimo e desigualdades funcionais em sistemas quânticos dissipativos”. J. Stat. Física. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

[38] Nilanjana Datta e Cambyse Rouzé. “Concentração de estados quânticos a partir de desigualdades funcionais quânticas e de custos de transporte”. J. Matemática. Física. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[39] Nilanjana Datta e Cambyse Rouzé. “Relacionando entropia relativa, transporte ideal e informação de Fisher: Uma desigualdade quântica de HWI”. Ana. Henri Poincaré 21, 2115–2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[40] François Golse, Clément Mouhot e Thierry Paul. “Sobre o campo médio e os limites clássicos da mecânica quântica”. Comum. Matemática. Física. 343, 165–205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[41] François Golse e Thierry Paul. “A equação de Schrödinger no campo médio e no regime semiclássico”. Arco. Ração. Mecânico. Anal. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[42] François Golse e Thierry Paul. “Pacotes de ondas e a distância quadrática de Monge-Kantorovich na mecânica quântica”. Comptes Rendus Matemática. 356, 177–197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

[43] Francisco Golse. “O problema quântico de $N$-corpos no campo médio e no regime semiclássico”. Fil. Trad. R.Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse e T. Paul. “O transporte quântico ideal é mais barato”. J. Stat. Física. 181, 149–162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[45] Emanuele Caglioti, François Golse e Thierry Paul. “Rumo ao transporte ideal para densidades quânticas”. arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma e Dario Trevisan. “Transporte quântico ótimo com canais quânticos”. Ana. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan e Seth Lloyd. “A distância quântica de Wasserstein de ordem 1”. IEEE Trans. Inf. Teoria 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole e Karol Życzkowski. “Problema quântico de Monge – Kantorovich e distância de transporte entre matrizes de densidade”. Física. Rev. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland e Karol Życzkowski. “Transporte quântico ótimo”. arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein e K. Życzkowski. “Monotonicidade de uma distância quântica de 2-Wasserstein”. J. Física. R: Matemática. Teoria. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos e Dániel Virosztek. “Isometrias quânticas de Wasserstein no espaço de estados qubit”. J. Matemática. Anal. Apl. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe e Seth Lloyd. “Complexidade Wasserstein de circuitos quânticos”. arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu e Seth Lloyd. “Aprendendo dados quânticos com a distância do motor quântico da terra”. Ciência Quântica. Tecnologia. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[54] EP Wigner e Mutsuo M. Yanase. “Conteúdo informativo das distribuições”. Processo. Nacional. Acad. Ciência. EUA 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki e Karol Horodecki. “Enredamento quântico”. Rev. Mod. Física 81, 865-942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[56] Otfried Gühne e Géza Tóth. “Detecção de emaranhamento”. Física. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik e Marcus Huber. “Certificação de emaranhamento da teoria à experiência”. Nat. Rev. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd e Lorenzo Maccone. “Medições aprimoradas quânticas: superando o limite quântico padrão”. Ciência 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

[59] Matteo G. A. Paris. “Estimativa quântica para tecnologia quântica”. Interno. J. Quant. Inf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[60] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna e Jan Kolodynski. “Capítulo quatro – Limites quânticos em interferometria óptica”. Programa. Óptica 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze e Augusto Smerzi. “Teoria quântica de estimativa de fase”. Em G. M. Tino e MA Kasevich, editores, Interferometria Atômica (Proc. Int. Escola de Física ‘Enrico Fermi’, Curso 188, Varenna). Páginas 691–741. IOS Press, Amsterdã (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Géza Tóth e Dénes Petz. “Propriedades extremas da variância e da informação quântica de Fisher”. Física. Rev.A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[63] Sixia Yu. “Informação Quântica de Fisher como Telhado Convexo de Variância”. arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

[64] Géza Tóth e Florian Fröwis. “Relações de incerteza com a variância e a informação quântica de Fisher baseada em decomposições convexas de matrizes de densidade”. Física. Rev. Pesquisa 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[65] Shao-Hen Chiew e Manuel Gessner. “Melhorando as relações de soma de incerteza com a informação quântica de Fisher”. Física. Rev. Pesquisa 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[66] CW Helstrom. “Teoria de detecção e estimativa quântica”. Imprensa Acadêmica, Nova York. (1976). url: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[67] A. S. Holevo. “Aspectos probabilísticos e estatísticos da teoria quântica”. Holanda do Norte, Amsterdã. (1982).

[68] Samuel L. Braunstein e Carlton M. Caves. “Distância estatística e a geometria dos estados quânticos”. Física Rev. Lett. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

[69] Samuel L Braunstein, Carlton M Caves e Gerard J Milburn. “Relações de incerteza generalizada: teoria, exemplos e invariância de Lorentz”. Ana. Física. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[70] Dénes Petz. “Teoria da informação quântica e estatística quântica”. Springer, Berlim, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[71] Géza Tóth e Iagoba Apellaniz. “Metrologia quântica na perspectiva da ciência da informação quântica”. J. Física. R: Matemática. Teoria. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied e Philipp Treutlein. “Metrologia quântica com estados não clássicos de conjuntos atômicos”. Rev. Mod. Física. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[73] Marco Barbieri. “Metrologia óptica quântica”. PRX Quantum 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

[74] Zoltán Leka e Dénes Petz. “Algumas decomposições de variâncias matriciais”. Provavelmente. Matemática. Estatista. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Dénes Petz e Dániel Virosztek. “Um teorema de caracterização para variâncias de matrizes”. Acta Sci. Matemática. (Szeged) 80, 681–687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

[76] Akio Fujiwara e Hiroshi Imai. “Um pacote de fibras sobre diversos canais quânticos e sua aplicação às estatísticas quânticas”. J. Física. R: Matemática. Teoria. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[77] BM Escher, RL de Matos Filho e L. Davidovich. “Estrutura geral para estimar o limite de precisão final em metrologia quântica ruidosa aprimorada”. Nat. Física. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński e Mădălin Guţă. “O indescritível limite de Heisenberg na metrologia quântica aprimorada”. Nat. Comum. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[79] Iman Marvian. “Interpretação operacional da informação quântica de Fisher em termodinâmica quântica”. Física. Rev. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

[80] Reinhard F. Werner. “Estados quânticos com correlações de Einstein-Podolsky-Rosen admitindo um modelo de variáveis ​​​​ocultas”. Física. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss e M. Lewenstein. “Correlações quânticas em sistemas de partículas indistinguíveis”. Ana. Física. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui e Nobuhiro Yonezawa. “Simetria de troca e emaranhamento multipartido”. Física. Rev.A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[83] Pawel Horodecki. “Critério de separabilidade e estados mistos inseparáveis ​​com transposição parcial positiva”. Física. Vamos. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[84] Asher Peres. “Critério de separabilidade para matrizes de densidade”. Física Rev. Lett. 77, 1413-1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki e Ryszard Horodecki. “O emaranhamento vinculado pode ser ativado”. Física. Rev. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

[86] Géza Tóth e Tamás Vértesi. “Estados quânticos com transposta parcial positiva são úteis para metrologia”. Física. Rev. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

[87] Scott Hill e William K. Wootters. “Enredamento de um par de bits quânticos”. Física. Rev. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

[88] William K. Wootters. “Enredamento da formação de um estado arbitrário de dois qubits”. Física Rev. Lett. 80, 2245–2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal e Armin Uhlmann. “Enredamento de assistência”. quant-ph/9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: quant-ph / 9803033

[90] John A. Smolin, Frank Verstraete e Andreas Winter. “Enredamento de assistência e destilação estatal multipartida”. Física. Rev.A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[91] Holger F. Hofmann e Shigeki Takeuchi. “Violação das relações de incerteza local como assinatura de emaranhamento”. Física. Rev.A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[92] Otfried Guhne. “Caracterizando o emaranhamento via relações de incerteza”. Física. Rev. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth e Peter Adam. “Os critérios de emaranhamento baseados em relações de incerteza locais são estritamente mais fortes do que o critério de norma cruzada computável”. Física. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza e Géza Tóth. “Spin espremendo desigualdades para spin arbitrário”. Física. Rev. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

[95] AR Edmonds. “Momento angular na mecânica quântica”. Imprensa da Universidade de Princeton. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[96] Géza Toth. “Detecção de emaranhamento em redes ópticas de átomos bosônicos com medições coletivas”. Física. Rev.A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne e Hans J. Briegel. “Desigualdades ideais de compressão de spin detectam emaranhamento limitado em modelos de spin”. Física. Rev. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

[98] Géza Tóth e Morgan W Mitchell. “Geração de estados singletos macroscópicos em conjuntos atômicos”. Novo J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[99] Géza Toth. “Detecção de emaranhamento multipartido na vizinhança de estados simétricos de Dicke”. J. Op. Soc. Sou. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

[100] Géza Tóth, Tobias Moroder e Otfried Gühne. “Avaliando medidas de emaranhamento de telhados convexos”. Física. Rev. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

[101] Lieven Vandenberghe e Stephen Boyd. “Programação semidefinida”. Revisão SIAM 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[102] Géza Toth. “Enredamento multipartido e metrologia de alta precisão”. Física. Rev.A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé e Augusto Smerzi. “Informação de Fisher e emaranhamento de multipartículas”. Física. Rev.A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki e Ryszard Horodecki. “Ativando utilidade metrológica oculta”. Física. Rev. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo e Federico M. Spedalieri. “Distinguir estados separáveis ​​e emaranhados”. Física. Rev. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo e Federico M. Spedalieri. “Família completa de critérios de separabilidade”. Física. Rev.A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo e Federico M. Spedalieri. “Detectando emaranhamento multipartido”. Física. Rev.A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[108] Harold Ollivier e Wojciech H. Zurek. “Discordância quântica: uma medida da quantumidade das correlações”. Física Rev. Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

[109] L. Henderson e V. Vedral. “Correlações clássicas, quânticas e totais”. J. Física. R: Matemática. Gênesis 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) e Ujjwal Sen. “Discordância quântica e seus aliados: uma revisão do progresso recente”. Rep. Física. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

[111] Dénes Petz. “Covariância e informações de Fisher em mecânica quântica”. J. Física. R: Matemática. Gênesis 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[112] Paolo Gibilisco, Fumio Hiai e Dénes Petz. “Covariância quântica, informação quântica de Fisher e as relações de incerteza”. IEEE Trans. Inf. Teoria 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[113] D. Petz e C. Ghinea. “Introdução à informação quântica de Fisher”. Volume 27, páginas 261–281. Científico Mundial. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[114] Frank Hansen. “Informações de distorção ajustadas pela métrica”. Processo. Nacional. Acad. Ciência. EUA 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami e Frank Hansen. “Uma abordagem unificada para a incerteza quântica local e poder interferométrico por informações de distorção ajustada métrica”. Entropia 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[116] MATLAB. “9.9.0.1524771(r2020b)”. Natick, Massachusetts (2020).

[117] MOSEK ApS. “A caixa de ferramentas de otimização MOSEK para o manual MATLAB. Versão 9.0”. (2019). url: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[118] J. Löfberg. “YALMIP: Uma caixa de ferramentas para modelagem e otimização em MATLAB”. Nos Anais da Conferência CACSD. Taipé, Taiwan (2004).

[119] Géza Toth. “QUBIT4MATLAB V3.0: Um pacote de programas para ciência da informação quântica e óptica quântica para MATLAB”. Computação. Física. Comum. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[120] O pacote QUBIT4MATLAB está disponível em https:/​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433, e na página pessoal https:/​/​gtoth.eu/​qubit4matlab.html.
https://www.mathworks.com/​matlabcentral/​fileexchange/​8433

Citado por

[1] Laurent Lafleche, “Transporte quântico ótimo e topologias fracas”, arXiv: 2306.12944, (2023).

As citações acima são de SAO / NASA ADS (última atualização com êxito 2023-10-16 14:47:44). A lista pode estar incompleta, pois nem todos os editores fornecem dados de citação adequados e completos.

Não foi possível buscar Dados citados por referência cruzada durante a última tentativa 2023-10-16 14:47:42: Não foi possível buscar os dados citados por 10.22331 / q-2023-10-16-1143 do Crossref. Isso é normal se o DOI foi registrado recentemente.

Este artigo é publicado na Quantum sob o Atribuição 4.0 do Creative Commons Internacional (CC BY 4.0) licença. Os direitos autorais permanecem com os detentores originais, como os autores ou suas instituições.

Carimbo de hora:

Mais de Diário Quântico