Maiorização contínua no espaço de fase quântica

Maiorização contínua no espaço de fase quântica

Carimbo de data / hora: 24 de maio de 2023 7:39
Nó Fonte: 2674950

Zacharie Van Herstraeten1,2, Michael G. Jabbour1,3,4e Nicolas J. Cerf1

1Centro de Informação e Comunicação Quântica, École polytechnique de Bruxelles, CP 165/59, Université libre de Bruxelles, 1050 Bruxelas, Bélgica
2Wyant College of Optical Sciences, Universidade do Arizona, 1630 E. University Blvd., Tucson, AZ 85721, EUA
3DAMTP, Centro de Ciências Matemáticas, Universidade de Cambridge, Cambridge CB3 0WA, Reino Unido
4Departamento de Física, Universidade Técnica da Dinamarca, 2800 Kongens Lyngby, Dinamarca

Acha este artigo interessante ou deseja discutir? Scite ou deixe um comentário no SciRate.

Sumário

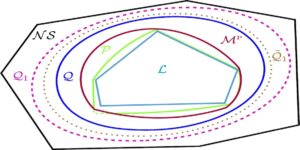
Exploramos o papel da teoria da majorização no espaço de fase quântica. Para este propósito, nos restringimos aos estados quânticos com funções de Wigner positivas e mostramos que a versão contínua da teoria da majoração fornece uma abordagem elegante e muito natural para explorar as propriedades teóricas da informação das funções de Wigner no espaço de fase. Depois de identificar todos os estados puros gaussianos como equivalentes no sentido preciso de majoração contínua, que pode ser entendido à luz do teorema de Hudson, conjecturamos uma relação de majoração fundamental: qualquer função de Wigner positiva é majorada pela função de Wigner de um estado puro gaussiano (especialmente , o estado de vácuo bosônico ou estado fundamental do oscilador harmônico). Como consequência, qualquer função côncava de Schur da função Wigner é limitada inferiormente pelo valor que assume para o estado de vácuo. Isto implica, por sua vez, que a entropia de Wigner é limitada inferiormente pelo seu valor para o estado de vácuo, enquanto o inverso não é notavelmente verdadeiro. Nosso principal resultado é então provar esta relação de majoração fundamental para um subconjunto relevante de estados quânticos positivos para Wigner que são misturas dos três estados próprios mais baixos do oscilador harmônico. Além disso, a conjectura também é apoiada por evidências numéricas. Concluímos discutindo algumas implicações desta conjectura no contexto das relações de incerteza entrópica no espaço de fases.

Resumo popular

O princípio da incerteza é um dos fenômenos mais fascinantes da física quântica. Embora possa parecer natural que pares de quantidades mensuráveis, como a posição e o momento de uma partícula, possam ser previstos simultaneamente com precisão, a física quântica na verdade proíbe isso para observáveis ​​não comutáveis. Heisenberg e Kennard tornaram isso preciso ao empregar a variância de qualquer quantidade mensurável para capturar sua incerteza. Anos mais tarde, o princípio da incerteza de Heisenberg foi reformulado recorrendo à entropia como um meio adequado para quantificar a incerteza. Aqui, introduzimos um paradigma teórico da informação ainda mais forte para a compreensão da incerteza das variáveis ​​quânticas no espaço de fase, nomeadamente a teoria da majorização.

Esta teoria matemática foi desenvolvida há mais de um século e tem sido usada em vários campos da ciência, desde estatística até física. Notavelmente, só foi aplicado à física quântica há relativamente pouco tempo, onde se mostrou ser uma abordagem poderosa para explorar o emaranhamento quântico. Como tal, nunca foi explorado para caracterizar as densidades contínuas que descrevem variáveis ​​quânticas no espaço de fase, ou seja, funções de Wigner. Mostramos que a majoração contínua é uma ferramenta adequada para isso. O principal objetivo do nosso artigo diz respeito à afirmação de que a função de Wigner do estado de vácuo de um modo bosônico (ou seja, o estado fundamental do oscilador harmônico) aumenta continuamente qualquer outra função de Wigner, tornando-a menos incerta no sentido de majoração. .

Embora exponhamos e discutamos nossos resultados no contexto da óptica quântica, eles são transferidos para qualquer par canônico e devem, portanto, ter implicações em diversas áreas da física.

► dados BibTeX

► Referências

[1] GH Hardy, JE Littlewood e G. Pólya, “Desigualdades”. Imprensa da Universidade de Cambridge, 1934.
https: / / doi.org/ 10.2307 / 3605504

[2] AW Marshall, I. Olkin e BC Arnold, “Desigualdades: Teoria da Majorização e suas Aplicações”, vol. 143. Springer, segunda edição, 2011.
https:/​/​doi.org/​10.1007/​978-0-387-68276-1

[3] T. Ando, ​​“Majorização, matrizes duplamente estocásticas e comparação de valores próprios”, Linear Algebra Appl. 118, 163–248 (1989).
https:/​/​doi.org/​10.1016/​0024-3795(89)90580-6

[4] K. Mosler, “Majorização em medidas de disparidade econômica”, Linear Algebra and its Applications 199, 91–114 (1994).
https:/​/​doi.org/​10.1016/​0024-3795(94)90343-3

[5] T. van Erven e P. Harremoës, “Rényi divergence and majorization”, em 2010 IEEE International Symposium on Information Theory, pp. 1335.
https: / / doi.org/ 10.1109 / ISIT.2010.5513784

[6] M. A. Alhejji e G. Smith, “A Tight Uniform Continuity Bound for Equivocation”, em 2020 IEEE International Symposium on Information Theory (ISIT), pp. 2270.
https: / / doi.org/ 10.1109 / ISIT44484.2020.9174350

[7] M. G. Jabbour e N. Datta, “Um limite de continuidade uniforme e rígido para a entropia condicional de Arimoto-Rényi e sua extensão aos estados quânticos clássicos”, IEEE Transactions on Information Theory 68, 2169–2181 (2022).
https: / / doi.org/ 10.1109 / TIT.2022.3142812

[8] A. Horn, “Matrizes Duplamente Estocásticas e a Diagonal de uma Matriz de Rotação”, American Journal of Mathematics 76, 620–630 (1954).
https: / / doi.org/ 10.2307 / 2372705

[9] MA Nielsen, “Condições para uma classe de transformações de emaranhamento”, Physical Review Letters 83, 436 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.83.436

[10] MA Nielsen e G. Vidal, “Majorização e interconversão de estados bipartidos”, Quantum Information and Computation 1, 76–93 (2001).
https: / / doi.org/ 10.26421 / QIC1.1-5

[11] M. A. Nielsen e J. Kempe, “Estados separáveis ​​são mais desordenados globalmente do que localmente”, Physical Review Letters 86, 5184–5187 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.86.5184

[12] T. Hiroshima, “Critério de majorização para destilabilidade de um estado quântico bipartido”, Physical Review Letters 91, 057902 (2003).
https: / / doi.org/ 10.1103 / PhysRevLett.91.057902

[13] Z. Puchala, Ł. Rudnicki e K. Życzkowski, “Majorização relações de incerteza entrópica”, Journal of Physics A: Mathematical and Theoretical 46, 272002 (2013).
https:/​/​doi.org/​10.1088/​1751-8113/​46/​27/​272002

[14] L. Rudnicki, Z. Puchała e K. Życzkowski, “Relações de incerteza entrópica de forte majorização”, Physical Review A 89, 052115 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.89.052115

[15] L. Rudnicki, “Abordagem de majorização para relações de incerteza entrópica para observáveis ​​de granulação grossa”, Physical Review A 91, 032123 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.91.032123

[16] F. Brandão, M. Horodecki, N. Ng, J. Oppenheim e S. Wehner, “As segundas leis da termodinâmica quântica”, Proceedings of the National Academy of Sciences 112, 3275–3279 (2015).
https: / / doi.org/ 10.1073 / pnas.1411728112

[17] R. García-Patrón, C. Navarrete-Benlloch, S. Lloyd, J. H. Shapiro e NJ Cerf, “Abordagem da Teoria da Majorização para a Conjectura de Entropia Mínima do Canal Gaussiano”, Physical Review Letters 108, 110505 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.110505

[18] C. N. Gagatsos, O. Oreshkov e NJ Cerf, “Relações de majorização e geração de emaranhamento em um divisor de feixe”, Physical Review A 87, 042307 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.042307

[19] G. De Palma, D. Trevisan e V. Giovannetti, “Estados passivos otimizam a saída de canais quânticos gaussianos bosônicos”, IEEE Transactions on Information Theory 62, 2895–2906 (2016).
https: / / doi.org/ 10.1109 / TIT.2016.2547426

[20] MG Jabbour, R. García-Patrón e NJ Cerf, “Preservação da majorização de canais bosônicos gaussianos”, New Journal of Physics 18, 073047 (2016).
https:/​/​doi.org/​10.1088/​1367-2630/​18/​7/​073047

[21] MG Jabbour e NJ Cerf, “Maiorização Fock em canais quânticos bosônicos com um ambiente passivo”, Journal of Physics A: Mathematical and Theoretical 52, 105302 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​aaf0d2

[22] U. Leonhardt, “Óptica quântica essencial: das medições quânticas aos buracos negros”. Imprensa da Universidade de Cambridge, 2010.
https: / / doi.org/ 10.1017 / CBO9780511806117

[23] A. Hertz, MG Jabbour e NJ Cerf, “Relações de incerteza entre entropia e poder: em direção a uma desigualdade estreita para todos os estados puros gaussianos”, Journal of Physics A: Mathematical and Theoretical 50, 385301 (2017).
https: / / doi.org/ 10.1088 / 1751-8121 / aa852f

[24] A. Hertz e NJ Cerf, “Relações de incerteza entrópica de variável contínua”, Journal of Physics A: Mathematical and Theoretical 52, 173001 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​ab03f3

[25] C. Weedbrook, S. Pirandola, R. García-Patrón, NJ Cerf, TC Ralph, JH Shapiro e S. Lloyd, “Informação quântica gaussiana”, Review of Modern Physics 84, 621–669 (2012).
https: / / doi.org/ 10.1103 / RevModPhys.84.621

[26] Z. Van Herstraeten e NJ Cerf, “Entropia Quantum Wigner”, Physical Review A 104, 042211 (2021).
https: / / doi.org/ 10.1103 / PhysRevA.104.042211

[27] FJ Narcowich, “Distribuições de tipo $ hbar $ positivo e aplicações”, Journal of mathematical Physics 30, 2565–2573 (1989).
https: / / doi.org/ 10.1063 / 1.528537

[28] T. Bröcker e R. Werner, “Estados mistos com funções Wigner positivas”, Journal of mathematical Physics 36, 62–75 (1995).
https: / / doi.org/ 10.1063 / 1.531326

[29] RL Hudson, “Quando a densidade de quase probabilidade de Wigner é não negativa?”, Reports on Mathematical Physics 6, 249–252 (1974).
https:/​/​doi.org/​10.1016/​0034-4877(74)90007-X

[30] F. Soto e P. Claverie, "Quando é a função Wigner de sistemas multidimensionais não-negativos?", Journal of Mathematical Physics 24, 97-100 (1983).
https: / / doi.org/ 10.1063 / 1.525607

[31] F. J. Narcowich e R. O'Connell, “Condições necessárias e suficientes para que uma função de espaço de fase seja uma distribuição de Wigner”, Physical Review A 34, 1 (1986).
https: / / doi.org/ 10.1103 / PhysRevA.34.1

[32] A. Mandilara, E. Karpov e NJ Cerf, “Estendendo o teorema de Hudson para estados quânticos mistos”, Physical Review A 79, 062302 (2009).
https: / / doi.org/ 10.1103 / PhysRevA.79.062302

[33] A. Mandilara, E. Karpov e N. Cerf, “Limites de gaussianidade para estados mistos quânticos com uma função Wigner positiva”, em Journal of Physics: Conference Series, vol. 254, pág. 012011, Publicação IOP. 2010.
https:/​/​doi.org/​10.1088/​1742-6596/​254/​1/​012011

[34] L. Wang e M. Madiman, “Além da desigualdade de poder da entropia, por meio de rearranjos”, IEEE Transactions on Information Theory 60, 5116–5137 (2014).
https: / / doi.org/ 10.1109 / TIT.2014.2338852

[35] GH Hardy, JE Littlewood e G. Pólya, “Algumas desigualdades simples satisfeitas por funções convexas”, Messenger of Mathematics 58, 145–152 (1929).

[36] H. Joe, “Uma ordenação de dependência para distribuição de k-tuplas, com aplicações para jogos de loteria”, Canadian Journal of Statistics 15, 227–238 (1987).
https: / / doi.org/ 10.2307 / 3314913

[37] I. Schur, “Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten”, Sitzungsberichte der Berliner Mathematischen Gesellschaft 22, 416–427 (1923).

[38] AW Roberts e DE Varberg, “Funções convexas”. Academic Press Nova York, 1973.
https:/​/​doi.org/​10.1016/​B978-0-444-89597-4.50013-5

[39] A. Rényi, “Sobre medidas de entropia e informação”, em Anais do Quarto Simpósio de Berkeley sobre Estatística Matemática e Probabilidade, Volume 1: Contribuições para a Teoria da Estatística, vol. 4, pp. 547–562, University of California Press. 1961.

[40] Y. He, AB Hamza e H. Krim, “Uma medida de divergência generalizada para registro robusto de imagens”, IEEE Transactions on Signal Processing 51, 1211–1220 (2003).
https://​/​doi.org/​10.1109/​TSP.2003.810305

[41] JV Ryff, “Órbitas de funções $ L ^ 1 $ sob transformações duplamente estocásticas”, Transactions of the American Mathematical Society 117, 92–100 (1965).
https: / / doi.org/ 10.2307 / 1994198

[42] F. Bahrami, S. M. Manjegani e S. Moein, “Operadores semi-duplamente estocásticos e majorização de funções integráveis”, Boletim da Sociedade de Ciências Matemáticas da Malásia 44, 693–703 (2021).
https:/​/​doi.org/​10.1007/​s40840-020-00971-2

[43] SM Manjegani e S. Moein, “Majorização e operadores semiduplamente estocásticos em $ L^{1}(X)$,” Journal of Inequalities and Applications 2023, 1–20 (2023).
https: / / doi.org/ 10.1186 / s13660-023-02935-z

[44] I. Białynicki-Birula e J. Mycielski, “Relações de incerteza para entropia de informação em mecânica ondulatória”, Communications in Mathematical Physics 44, 129–132 (1975).
https: / / doi.org/ 10.1007 / BF01608825

[45] A. Wehrl, “Propriedades gerais da entropia”, Reviews of Modern Physics 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[46] EH Lieb, “Prova de uma conjectura de entropia de Wehrl”, em Desigualdades, pp. Springer, 359.
https:/​/​doi.org/​10.1007/​978-3-642-55925-9_30

[47] EH Lieb e JP Solovej, “Prova de uma conjectura de entropia para estados de spin coerentes de Bloch e suas generalizações”, Acta Mathematica 212, 379 (2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[48] JR Johansson, PD Nation e F. Nori, “QuTiP: Uma estrutura Python de código aberto para a dinâmica de sistemas quânticos abertos”, Computer Physics Communications 183, 1760–1772 (2012).
https: / / doi.org/ 10.1016 / j.cpc.2012.02.021

[49] K. Życzkowski, P. Horodecki, A. Sanpera e M. Lewenstein, “Volume do conjunto de estados separáveis”, Physical Review A 58, 883 (1998).
https: / / doi.org/ 10.1103 / PhysRevA.58.883

Citado por

[1] Nuno Costa Dias e João Nuno Prata, “Sobre uma conjectura recente de Z. Van Herstraeten e N.J. Cerf para a entropia quântica de Wigner”, arXiv: 2303.10531, (2023).

[2] Zacharie Van Herstraeten e Nicolas J. Cerf, “Entropia Quantum Wigner”, Revisão Física A 104 4, 042211 (2021).

[3] Martin Gärttner, Tobias Haas e Johannes Noll, “Detectando emaranhamento variável contínuo no espaço de fase com a distribuição $Q$”, arXiv: 2211.17165, (2022).

As citações acima são de SAO / NASA ADS (última atualização com êxito 2023-05-24 23:55:18). A lista pode estar incompleta, pois nem todos os editores fornecem dados de citação adequados e completos.

On Serviço citado por Crossref nenhum dado sobre a citação de trabalhos foi encontrado (última tentativa 2023-05-24 23:55:17).

Este artigo é publicado na Quantum sob o Atribuição 4.0 do Creative Commons Internacional (CC BY 4.0) licença. Os direitos autorais permanecem com os detentores originais, como os autores ou suas instituições.

Carimbo de hora:

Mais de Diário Quântico